一種基于Zieloger-Niclosls法的反應堆堆芯功率PID串級控制器整定方法研究

何伯陽，吳 茜，黃 勇

（中廣核研究院有限公司 北京分公司，北京 100086）

0 引言

目前，某型在研實驗動力堆采用“折線型”雙恒定方案，即高于一定功率時，一回路平均溫度恒定、OTSG出口壓力恒定的“雙恒定”總體控制策略[1]。因而提出了對堆芯平均溫度的控制要求。

然而，在該型反應堆實際工作過程中，冷卻劑硼濃度波動、溫度負反饋和燃料多普勒效應會引起堆芯反應性擾動，從而導致反應堆功率波動[2]。同時，堆芯下腔室冷卻劑入口溫度、主泵轉速變化也會引起反應堆堆芯溫度波動[2]。溫度波動效應和反應性波動效應疊加，從而影響到“折線型”雙恒定方案的實現。因此，為了保障反應堆能按照設定水平輸出功率，需要設計一個專用的“溫度-功率”控制器，以實現對堆芯溫度、功率的控制。

1 堆芯系統開環控制學模型

為了設計該實驗動力堆控制系統，需要準確建立被控過程的數學模型，然后依據該模型，按照控制需求來設計控制器。由于目前尚未建立實驗堆，不具備實驗辨識條件。因此，本文主要采用解析建模法在已有設計參數的基礎上建立堆芯系統的模型。

圖1 堆芯熱工水力學模型Fig.1 Thermo-hydraulic model of core reactor

解析建模法就是針對建模對象，建立各種平衡方程，如：質量守恒方程、能量守恒方程、動量平衡方程，通過微分方程組來描述系統動力學特性，即是系統的狀態空間描述。通過線性化狀態空間方程，可求得系統的傳遞函數矩陣。

1.1 堆芯物理模型

在反應堆系統設計中，點堆方程是主要的非線性環節。在穩態工作點鄰域內，點堆方程可以線性化，由此建立系統的傳遞函數。

經典點堆方程如式（1）所示[3]：

其中：

nr(t) --t時刻的相對中子密度。

Cr(t) --t時刻的緩發中子先驅核相對密度。

ρ(t) --t時刻引入的反應性。

β--緩發中子總份額。

λ--緩發中子衰變常數，s-1。

1.2 堆芯熱工水力學模型

堆芯熱工動力學模型采用平均通道等效近似來處理，由于堆芯物理模型為點堆方程，不考慮堆芯功率分布。因此，燃料僅采用一個節點；由于采用集總參數法，所以冷卻劑則采用單個節點。示意圖如圖1所示。

其中：

Tf--燃料溫度，Co

Tc2--冷卻劑節點出口溫度，Co

Tlp--冷卻劑節點入口溫度，Co

Tavg--冷卻劑平均溫度，Co

1.3 燃料能量守恒方程

堆芯燃料的熱量變化率等于燃料產熱功率減去燃料傳遞給冷卻劑節點的熱功率，即如式（2）所示：

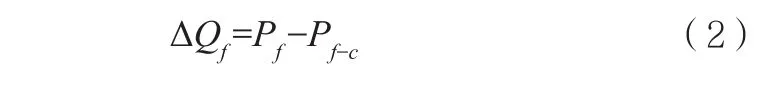
其中：ΔQf表示堆芯燃料的熱量變化率，Pf表示燃料產熱功率，Pf-c表示燃料傳遞給冷卻劑節點的熱功率。又因為燃料熱量變化率與燃料溫度變化率成以下關系：

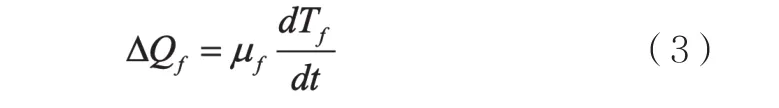
假設燃料中產生熱量占總功率的份額為f，則燃料產熱功率如下：

其中，PFLL表示實際功率，P0表示反應堆滿功率值，nr表示相對中子密度。

又由于傳熱公式可得：

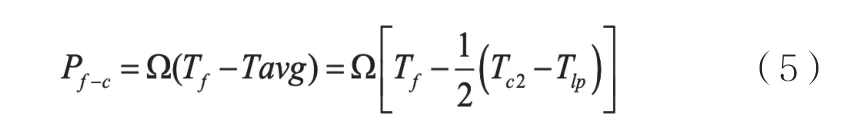
將式子代入上述方程式（5）可得：

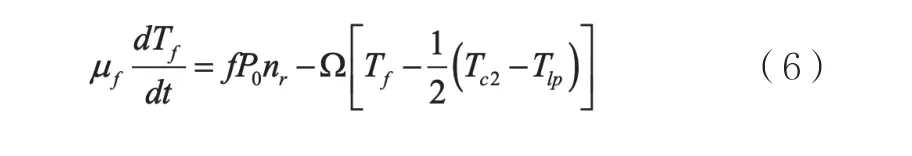
1.4 冷卻劑節點能量守恒方程

冷卻劑節點熱量變化率等于冷卻劑中產生的熱功率加燃料傳遞給冷卻劑的熱功率—冷卻劑流動帶走的熱功率，如下：

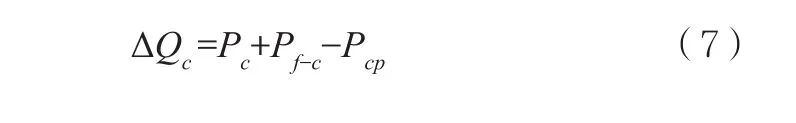
其中：ΔQc表示冷卻劑節點熱量變化率，Pc表示冷卻劑中產生的熱功率，Pf-c表示燃料傳遞給冷卻劑的熱功率，Pcp表示冷卻劑流動帶走的熱功率。附注：以上過程不考慮熱量散失。又因為冷卻劑熱量變化率與冷卻劑溫度變化率成以下關系：

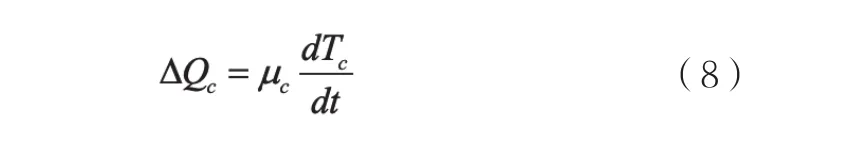
假設燃料中產生熱量占總功率的份額為f，則冷卻劑產熱占總功率的份額為（1-f）。因此，冷卻劑產熱功率如下：

又由于傳熱公式可得：

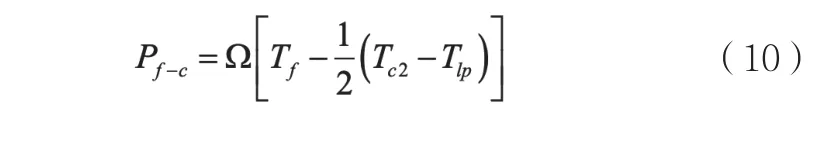
冷卻劑流動帶走的熱功率如下：

其中：Wp表示冷卻劑工質流量，Kpc表示工質熱容。可得：

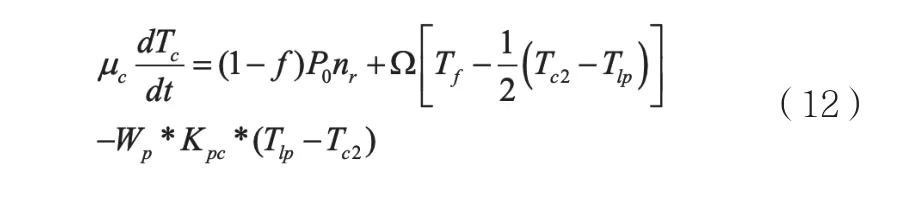
1.5 反應性調節

反應性反饋考慮了燃料與冷卻劑溫度作用，忽略氙等毒素引入的反應性反饋，即：總反應性等于控制棒引入的反應性減去燃料多普勒效應引入的負反應性減去冷卻劑引入的負反應性。

設控制棒引入的反應性為ρrod，燃料多普勒系數為αf，冷卻劑負溫度系數為αc，則總反應性如下：

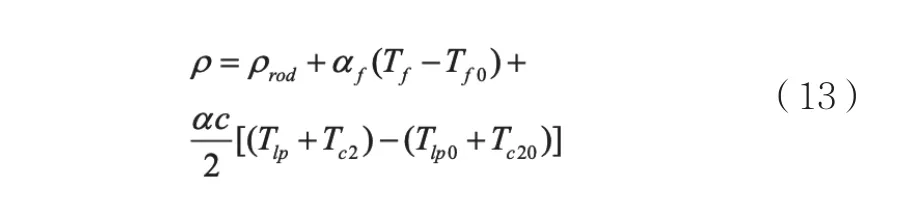
將式（13）反應性負反饋方程代入歸一化點堆方程（1）可得：

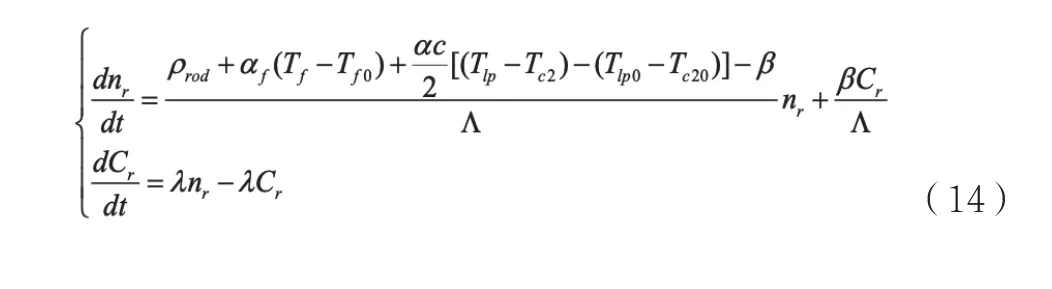
1.6 系統動力學微分方程組

在得到上述方程后，可以整理得到描述系統動力學特性的微分方程組如下：

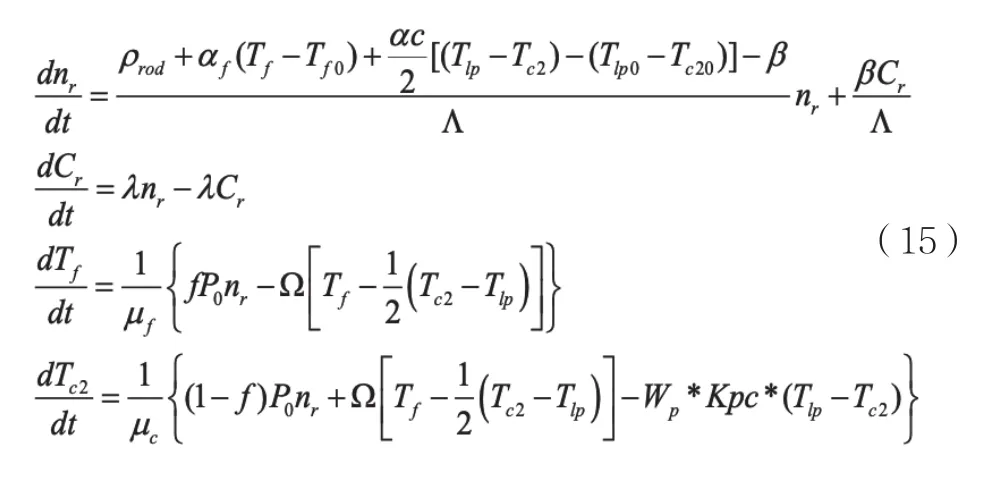
建立系統狀態空間表達式主要方法有兩種：第一種方法是根據系統的工作原理，選擇相關物理量作為系統的狀態變量，直接寫出狀態方程；第二種方法是根據系統的動力學微分方程組，推導出狀態方程[4]。本文采用第二種方法。

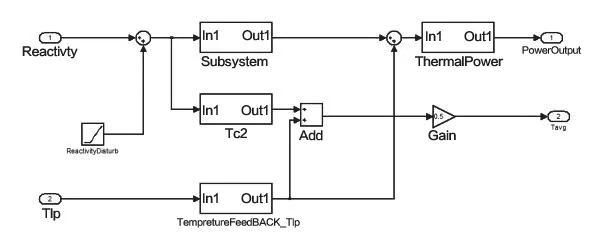
圖2 堆芯系統Matlab/Simulink模型Fig.2 Matlab/simulink Model of core system

建立系統的狀態空間表達式的第一步是選取狀態變量[5]。系統在時域空間中運動信息稱為狀態，確定系統狀態的一組獨立變量（數目最小）稱為狀態變量，它是能夠完整、確定的描述系統時域行為的最少的一組變量[6]。在上述微分方程組中，涉及到6個變量：nr，Cr，Tf，Tc2，ρrod，Tlp，其中ρrod，Tlp是人為輸入量。因此，僅憑nr，Cr，Tf，Tc2，就可以表征系統的狀態。所以選取系統狀態變量如下：

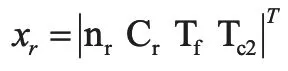
并以

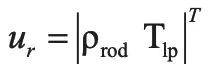
為輸入量。將前述微分方程改寫為以下形式：

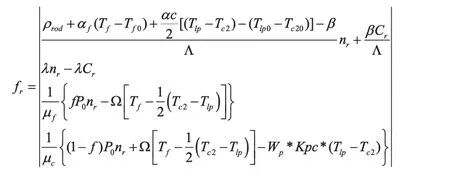
則有系統的狀態空間模型如下：

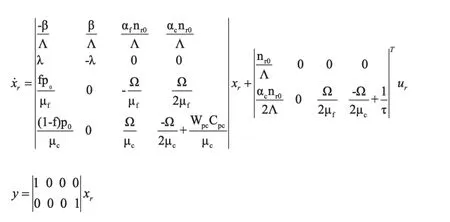
1.7 反應堆控制學模型

根據上述數學模型，結合該型動力實驗堆系統設計參數[7]，在Matlab/simulink中搭建系統的開環模型如圖2所示。

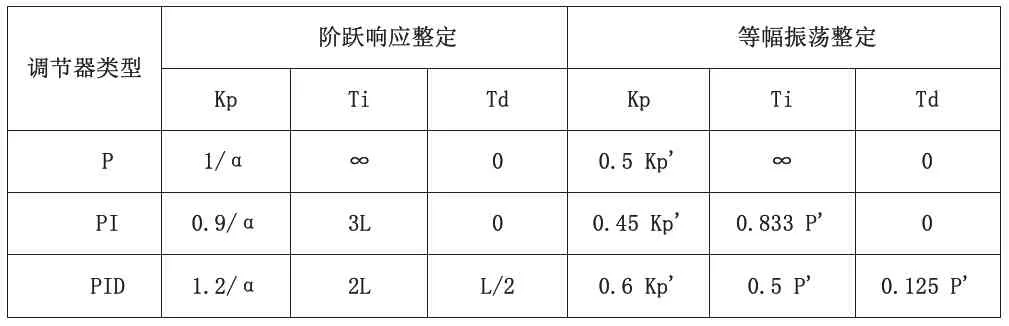
表1 PID控制器的有關參數整定關系表Table 1 Parameter setting relation table for PID controller

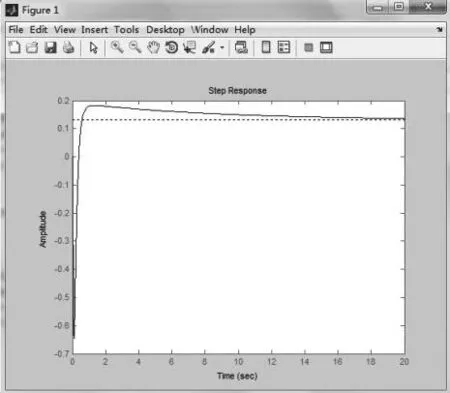
圖3 堆芯開環系統階躍響應曲線Fig.3 Step response curve of core open loop system

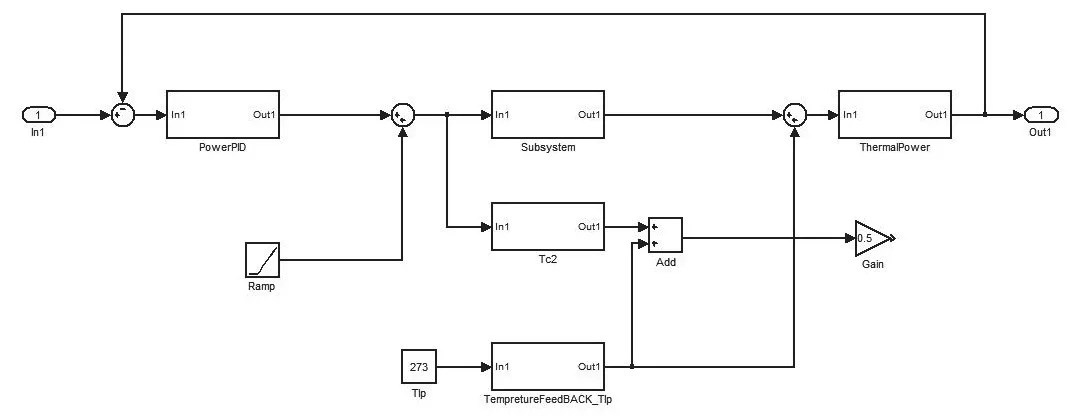
圖4 帶一級控制器的堆芯Matlab/Simulink模型Fig.4 Core Matlab/simulink model with first-level controller

2 PID 控制器解析化設計方法

PID控制器解析化設計方法的核心是由被控對象的數學模型直接得出PID 控制器的參數[8]。基于不同的控制要求和優化準則有多種設計方法，Zieloger-Niclosls法是一種常用方法[9]。

實現方法：設想對被控對象（開環系統）施加一個階躍信號，通過實驗方法，測出其響應信號。則輸出信號可由圖中的形狀近似確定參數k，L和T（或α，α=kL/T）。如果獲得了參數k，L和T（或α）后，則可根據表1確定PID控制器的有關參數[9]。

整定過程如下：

首先，對1.7節中模型施加階躍信號，獲得系統的階躍響應曲線。該部分用Matlab代碼實現，獲得階躍響應曲線如圖3所示。從該階躍響應曲線可以獲得3個主要參數k，L和T，并按照表1的關系計算出PID控制器3個整定值Kd，Ki，Kp。

其次，將上述參數填入一級串級控制器，得到系統的功率閉環模型如圖4所示。

對上述功率閉環模型再次施加階躍信號，獲得其階躍響應曲線，觀察該曲線參數，確保曲線負荷超調量、調節時間、穩態誤差等性能指標符合設計要求[1]。

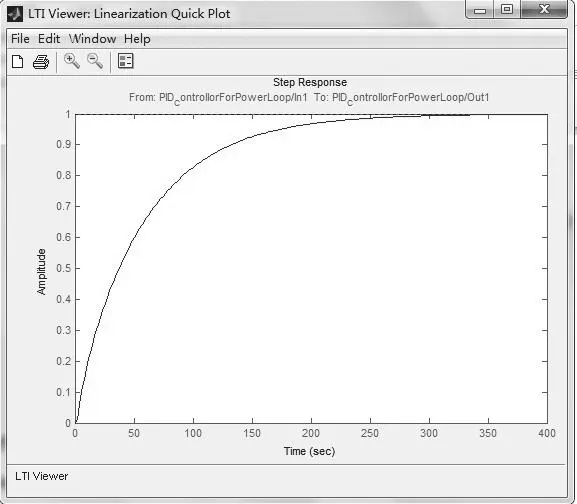
圖5 帶一級控制器的堆芯模型階躍響應曲線Fig.5 Step response curve of core model with primary controller

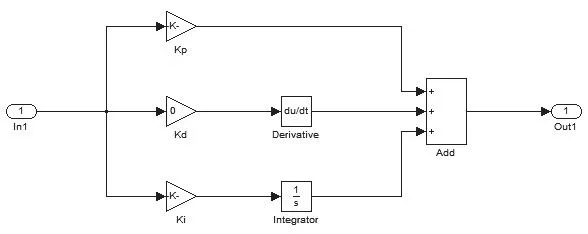
圖6 溫度閉環PID控制器Fig.6 Temperature closed-loop PID controller

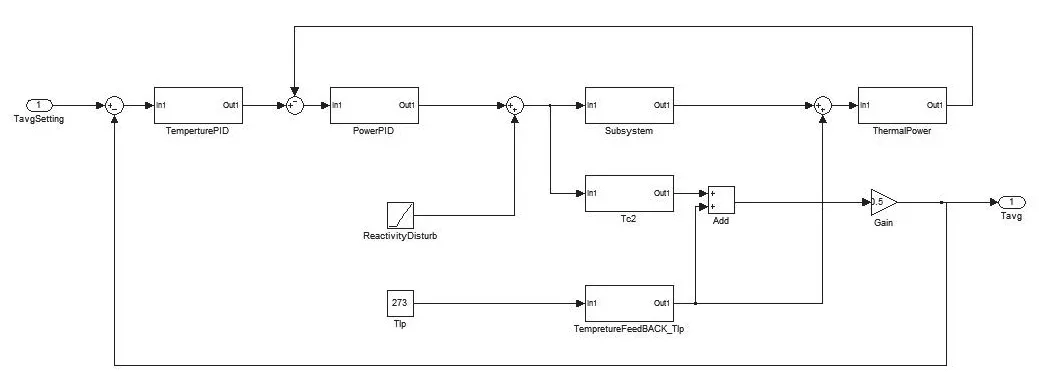
圖7 帶PI-PID串級控制器的堆芯溫度-功率控制系統Fig.7 Core temperature-power control system with PI-PID cascade controller

獲得了第一級功率PID控制器后，可以將功率控制器件和開環系統封裝為一個子系統，然后再添加一個溫度PID控制器，只要整定了溫度環PID 3個參數即可以獲得系統的PID控制器。由于一回路平均溫度受到堆芯入口溫度影響，所以波動較為頻繁，為了防止控制器頻繁動作導致控制性能惡化，溫度閉環控制器將微分環節參數取為零。只采用PI控制，具體結構如圖6所示。

該環節整定方法和功率整定方法類似，可以直接采用第一個控制器參數范圍內取值。令

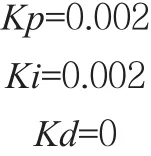
將上述參數填寫入控制器中，即得到帶參數的溫度PID控制器。得到了兩個閉環控制器后如圖7所示。

3 仿真結果分析

對上述閉環控制系統施加階躍信號，得到階躍響應曲線如圖8所示。

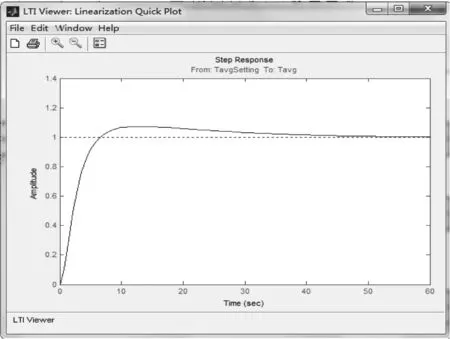
圖8 PI-PID串級控制器的堆芯溫度-功率控制系統階躍響應曲線Fig.8 Core temperature-power control system step response curve for PI-PID cascade controller

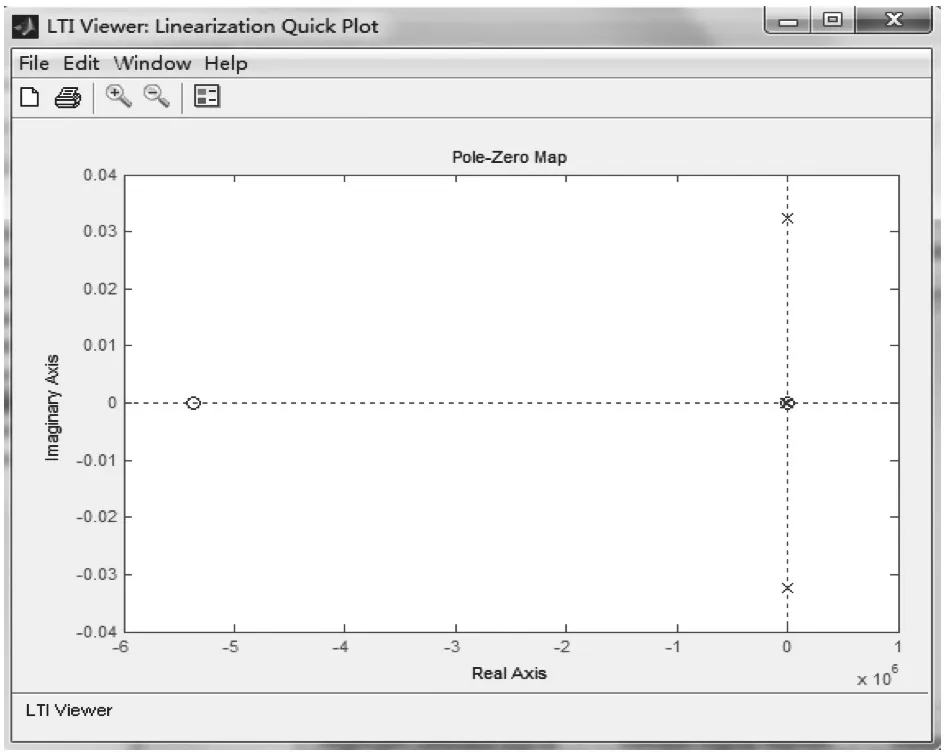
圖9 閉環系統零極點分布圖Fig.9 Closed-loop system 0 pole distribution

圖8階躍響應曲線，該控制系統可以較好地跟蹤階躍輸入信號。穩態誤差為零，穩態響應時間為6s～10s，超調量不超過穩態值的10%。因此，認為該控制系統滿足控制精度和響應速度的要求[9]。

同時，完成動態特性分析后，利用Matlab/Simulink環境下獲得其零極點分布如圖9所示。

從圖上可以看出，坐標軸右側沒有極點分布。通過經典控制理論判斷，該系統不會出現失穩定狀態[9]。同時坐標軸上有兩個極點，為了進一步提高使用的穩定性，可以再設計校正環節。通過改變系統零極點分布的方式來改善系統的響應特性。