火電廠AGC控制回路的非線性分析

歐陽春明，李慧霞，錢文華

（1.廣東電網有限責任公司 電力科學研究院，廣州 510080；2.北京協同創新智能電網技術有限公司，北京 100094）

0 引言

AGC是電網中發電機組調度與控制的一項重要內容，是實現電網有功功率控制、維持系統頻率質量以及互聯電網之間聯絡線功率控制的一種重要技術手段，其控制策略的優劣、模型辨識的精度等直接決定了AGC控制效果的好壞[1-4]。

正如非線性是任何系統都或多或少存在的特性一樣，所有火電廠熱工儀表、設備等也普遍輕重不一地具有非線性特性。諸如熱電偶溫度儀表中熱電勢和溫度的關系、節流式流量儀表中流量與壓差的關系都是非線性函數；火電單元機組包含由鍋爐、汽包、再熱器以及汽輪機等具有熱慣性、反應延遲的設備[5,6]。由這些具有非線性特性的熱工儀表以及設備所組成的AGC控制回路也必然存在一定的非線性特性，導致AGC控制回路的控制策略、建模等存在很大的難度。分析AGC控制回路的非線性特性能有助于明確其控制策略的制定、控制對象模型的辨識。

自回歸各態歷經ARX模型通過一個線性方程來描述系統輸入輸出之間的關系，被廣泛應用于線性系統分析[7,8]。神經網絡屬于人工智能領域，具備自學習能力，尤其適用于非線性系統的分析，并得到快速發展[9]。本文主要介紹ARX和神經網絡兩種系統分析方法，并通過火電廠AGC控制回路實際運行數據進行實驗分析，對兩種系統分析方法進行比較，研究AGC控制回路的非線性特性。

1 ARX模型分析

離散系統的輸入輸出模型可用差分方程的形式來表示[10-12]：

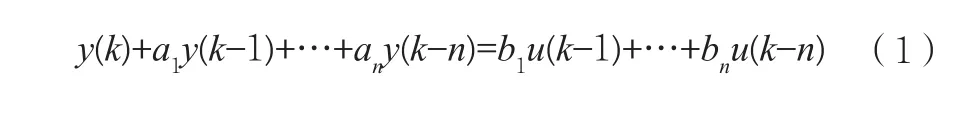
對式（1）進行z變換，在零初始條件下輸出變量的z變換對輸入變量的z變換之比就是該系統的z傳遞函數：

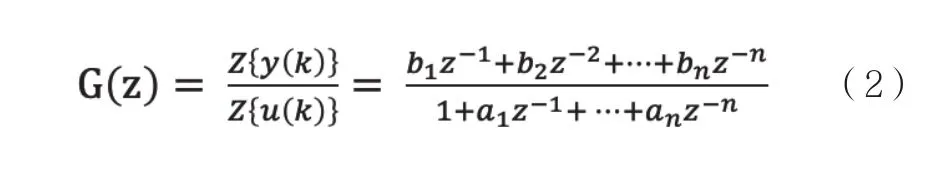
式（2）中，z為移位算子，它與運算子s的關系為：

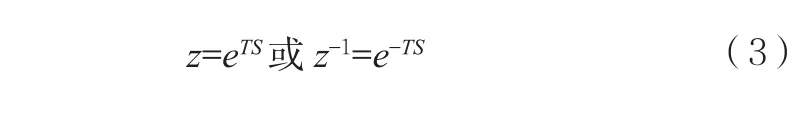
其中，T為采樣周期。移位算子的運算有如下的關系：

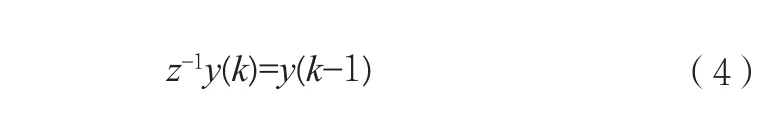
利用式（4），可容易地將式（2）的z的傳遞函轉換為式（1）的差分方程的形式。

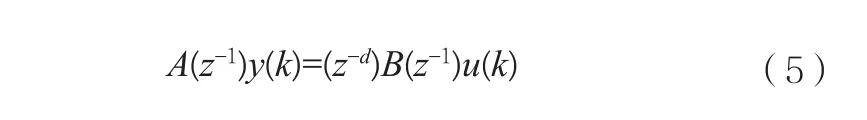
式（5）中：

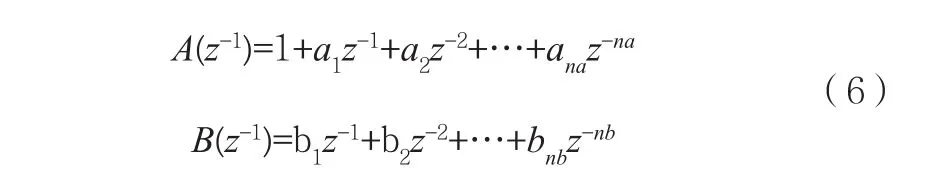
其中：na、nb和d是這類模型的結構參數，na、nb是A(z-1)和B(z-1)的階次，d是純滯后步數，純滯后時間即為dT。

如果上述的模型還受到噪聲的影響，則式（5）的模型可以進一步地寫成隨機性模型：

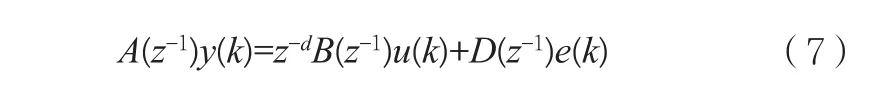
式（7）中：

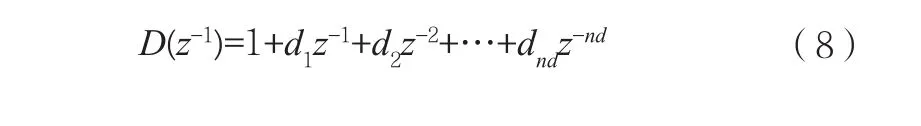
式（5）是確定性定常線性系統離散時間模型，而式（7）是隨機性定常線性系統離散時間模型。

式（7）通常使用最小二乘法進行求解，最小二乘法的一次完成算法如下，給定單輸入單輸出線性、定常、隨機系統的數學模型：

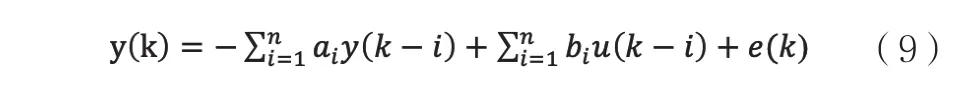
已知測量數據序列{u(k),y(k),k=1,2,…,n+N}，對式（9）所描述系統，辨識包括兩個問題：首先要確定階次n，這是結構辨識問題；在n確定后，求參數ai，bi這是參數估計問題。本文討論的問題為n已知的情況。

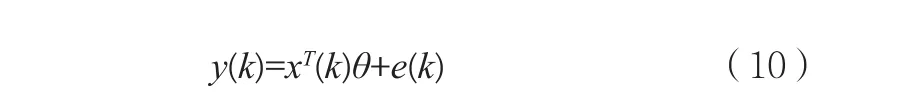
隨著方程（10）建立（y, x已知），能夠利用最小二乘法估計參數矢量θ[13]。極小化誤差函數J：

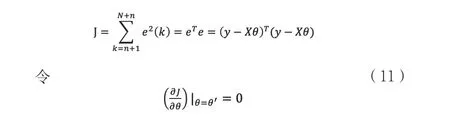
可得最小二乘估計值θ′=(X T X)-1X Ty，如果(X T X)是非奇異的，則此解存在。

2 神經網絡系統分析

神經網絡具有顯著的學習能力和高度的并行運算能力，為非線性系統分析提供了一條十分有效的途徑[14,15]。

針對火電廠具有大慣性、大延遲特性的熱工對象[16,17]，可以嘗試使用神經網絡的方法來建立其數據模型。利用現場自然存在的擾動及被控對象的輸出作為神經網絡辨識器的輸入，經過神經網絡辨識器的學習過程，來獲得系統的數學模型。

目前應用在系統辨識中的神經網絡主要有以下3種：單層神經網、Adaline神經網絡和B-P神經網絡。

由于現場存在各種無法預測的干擾信號，許多系統中間狀態的值是無法測量的，且系統階次一般無法預先得知或無法辨識得非常準確，這就限制了單層神經網絡在電廠中的應用[18]。

由于Adaline神經網絡存在缺點：一是設定的延遲器數目必須與系統階次相等，即系統階次必須已知或者辨識得非常準確，才能獲得滿意的辨識結果；二是網絡較脆弱、抗干擾能力差，這也限制了該網絡在電廠中的應用。

1989年Robert Hecht-Nielson證明了對任何在閉區間內的一個連續函數，都可以用一個隱層的B-P網絡來逼近，可以選用一個3層的B-P網絡進行辨識試驗。學習步長、辨識網絡的輸入層節點數、隱層節點數等會影響神經網絡的辨識精度。設計一個廣義的、適用的辨識網絡基本結構、盡可能減少辨識參數的反復、交叉調整，以達到預期的辨識精度是基本設計思想。

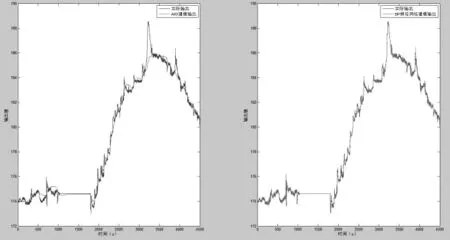
圖1 4500s實測數據下ARX和BP預測輸出比較Fig.1 The output by ARX and BP neural network

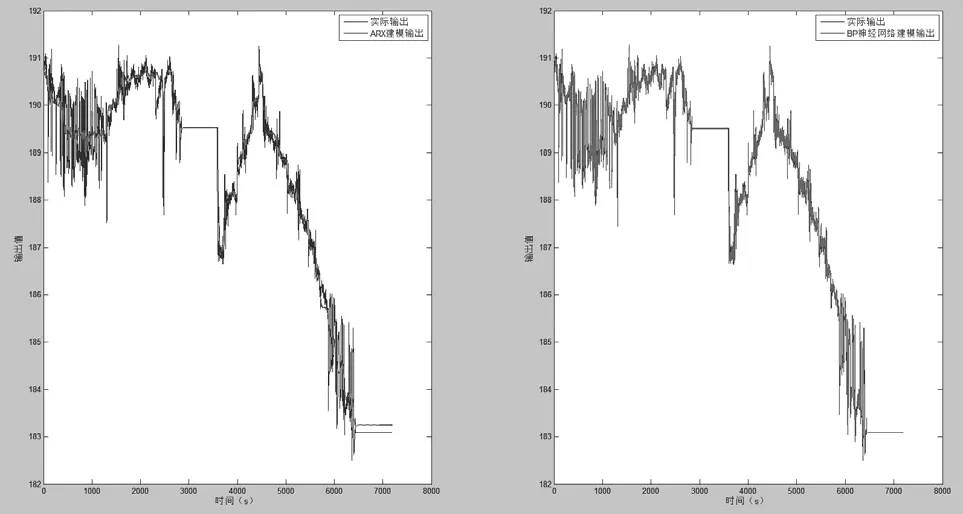
圖2 7200s實測數據下ARX和BP預測輸出比較Fig.2 The output by ARX and BP neural network

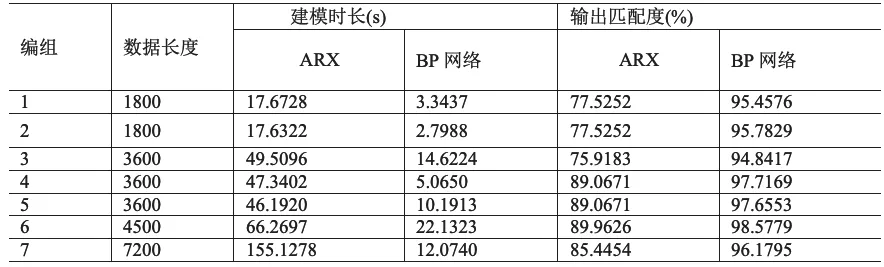
表1 ARX和BP神經網絡分析AGC回路數據結果比較Table 1 The analysis result with ARX and BP neural network

3 實驗結果分析

設受控對象模型為：

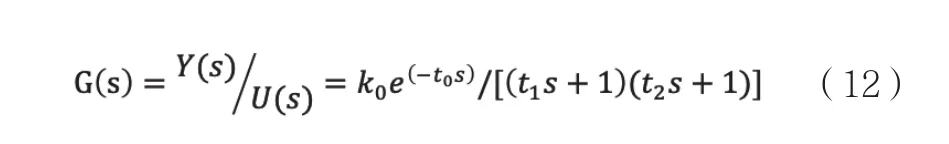
通過Z變換寫成差分方程形式

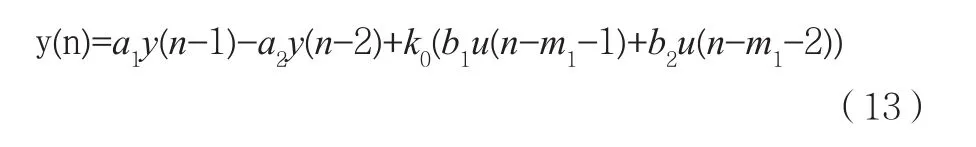
t1，t2為時間常數；k0為模型增益；t0為純滯后時間；n為采樣點數(n=1,2,…)。

設純滯后時間t0是采樣周期的整數倍，即t0=m1T，由式（13）可知網絡的輸入節點數為4，即輸入向量為p=[y(n-1)y(n-2)u(n-m1-1)u(n-m1-2)]，設隱層節點數目為4，一個輸出節點，此時受控對象模型網絡為4-4-1結構。

本文實驗數據采用某電廠AGC汽機主控回路的實測數據，數據主要包含實測輸出信號y、輸入信號u和干擾信號d。

按照公式（7），將以上實測輸出信號y、輸入信號u和干擾信號d，通過ARX方法建立最優的模型，并得到仿真輸出。

應用BP神經網絡對實測輸出信號y、輸入信號u和干擾信號d進行訓練，輸入向量p=[y(n-1)y(n-2)u(n-1)u(n-2)d(n-1)d(n-2)]，學習速率l=0.005，采樣時間間隔為1s。通過對網絡訓練可以得到對應的輸出。

本文采用7組實測數組對以上兩種方法進行比較，其中兩組數據（數據長度分別為4500s和7200s）的仿真輸出和實測輸出的曲線圖見圖1和圖2所示。從圖中可以看出，通過BP神經網絡辨識得到輸出與實際輸出曲線變化趨勢更一致。

通過比較7組數組的仿真輸出與實際輸出的匹配度，以及仿真時長如表1所示。

從表1可以看出，對于同一組數據，使用BP網絡進行系統分析得到的輸出匹配度明顯高于ARX方法，并且分析的速度也比ARX要快。隨著數據長度的增加，ARX分析時間呈線性增長，而BP網絡分析時間并不簡單的隨時間增長而增長，而是可能與數據的復雜度有關。

4 結論

本文通過ARX和BP神經網絡兩種方法，對火電廠AGC汽機主控回路實測數據進行了仿真分析，結果表明：BP神經網絡能夠更準確地分析和預測系統輸出，并且分析速度快；ARX系統模型的分析時間隨著數據長度的增加而呈線性增加；BP神經網絡在進行系統分析時，其時間隨著數據長度的增加而略微增加，甚至出現下降的情況，說明BP神經網絡系統分析的時間除了和數據長度有關外，可能還與數據本身的復雜度有關。

綜合以上，可以得出火電廠主控回路的數據分析使用BP神經網絡這一非線性分析方法精度高、速度快，說明火電廠主控回路存在明顯的非線性特性，使用二階慣性延遲系統能夠更好地描述火電廠AGC汽機主控回路的特性，在進行火電廠控制回路設計時應充分考慮其非線性。