Co、Ni和Ga合金化對DO19-Ti3Al彈性性能影響的第一性原理研究

張超彥 , 張麗霞 , 侯 華

(1. 徐州工業職業技術學院，徐州 221100; 2. 中北大學，太原 030051)

1 引 言

在可持續發展戰略下，航空及汽車等行業廣泛關注輕量化技術，對材料的比強度要求日益增加[1]. 全層片狀TiAl合金具有良好的高溫強度、比強度及比剛度等特點在輕量化設計中潛力巨大，研究者在成分設計、表面處理和加工方式等領域開展了廣泛的研究. 截至目前，室溫塑性較低依然制約其應用范圍，室溫塑性差的主要原因為γ相中的電荷方向性較強及α2相變形中晶界應力由于滑移系較少不能釋放產生脆性斷裂[2, 3]. 合金化被廣泛應用于TiAl合金的性能改善，對γ相，合金元素加入可以消弱其晶體內的電荷方向性從而改善其塑性；對α2相則主要是降低Ti-Ti鍵的強度從而改善其非基面滑移的阻力[4, 5].

隨著計算材料機技術的發展，采用計算方法研究材料的性能越來越普及，第一性原理研究被廣泛應用于TiAl合金. Liu[6]等采用第一性原理對α2-Ti3Al晶體的電子結構和彈性性能進行研究，并解釋了其變形機制；Music等[7, 8]研究了V、Nb和Ta對γ-TiAl晶體化學鍵的影響，發現這些元素可以改善其彈性性能，并且對V、Nb、Ta、Cr、Mo、W和Mn元素在α2相中的固溶體進行計算，得出其彈性常數并分析其電子結構，發現合金元素可以降低晶體中的共價鍵強度，從而提高合金的塑性；王海燕[9]通過不同濃度的固溶體模型研究了Mo元素濃度對γ-TiAl合金的性能影響，發現Mo元素濃度為12.5at.%可以顯著改善合金的塑性；Zhang等[10]的第一性研究發現Nb和Ta元素固溶降低α2-Ti3Al的塑性，但可以顯著提高其硬度.

合金元素對層片狀TiAl合金中主相的性能影響的研究已廣泛開展，但主要集中在γ相中，對于α2相的研究相對薄弱，合金元素種類也較少，截至目前未見Co、Ni和Ga元素對Do19結構的α2-Ti3Al的彈性性能和電子結構的相關報導. 由于Co元素做為常見的合金元素廣泛應用于高硬度合金和高溫合金，Ni元素做為合金元素通常改善材料的塑性及抗腐蝕性，Ga元素置換Al元素可以改善NiAl基合金的室溫塑性，故對此3種元素對Do19-Ti3Al的性能影響研究，為實驗提供理論基礎.

2 計算模型與方法

DO19-Ti3Al的晶體結構為密排六方結構，空間群No.194，其單胞模型由6個Ti原子和2個Al原子組成，原子坐標分別為(1/6,5/6,3/4) 和(1/3,2/3,1/4). 由于Ti和Al原子與M(M=Co、Ni和Ga)原子的半徑之比分別為1.05、1.06、0.94和1.13、1.15、1.0，均大于0.59，在Ti3Al晶體中M原子以置換原子的形式固溶[11]. 固溶體的計算模型采用1×1×2的Ti3Al超晶胞，其中包含12個Ti原子和4個Al原子，M原子置換其中的一個Ti原子(Al原子)，得到濃度6.25 %的Ti11Al4M(Ti12Al3M)晶體，如圖1所示.

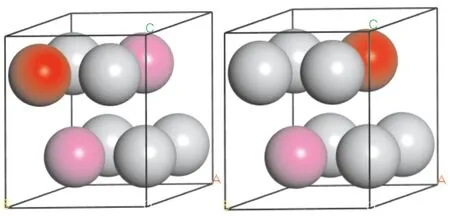
圖1 Ti11Al4M(Ti12Al3M)(M=Co、Ni和Ga)的晶體結構(其中：灰色球Ti原子，紫色球Al原子，紅色球M原子)Fig. 1 The crystal structure of Ti11Al4M (Ti12Al3M) (M=Co, Ni and Ga)

采用基于密度泛函理論的第一性原理MS程序包中CASTEP模塊，贗勢選取為超軟(Ultrasoft)贗勢，計算在倒易空間中的進行，勢能函數選擇廣義梯度近似的PBE和PW91兩種形式進行對比. 平面波截斷能Ecut和K點網格數的選取通過總能量收斂測試[12]，分別確定為410.0 eV和6×6×3. 計算收斂條件設置為：能量波動小于5×10-6eV/atom，作用力小于0.01 eV/?，應力小于0.02 GPa，位移小于5×10-4?.

3 計算結果與分析

3.1 幾何結構

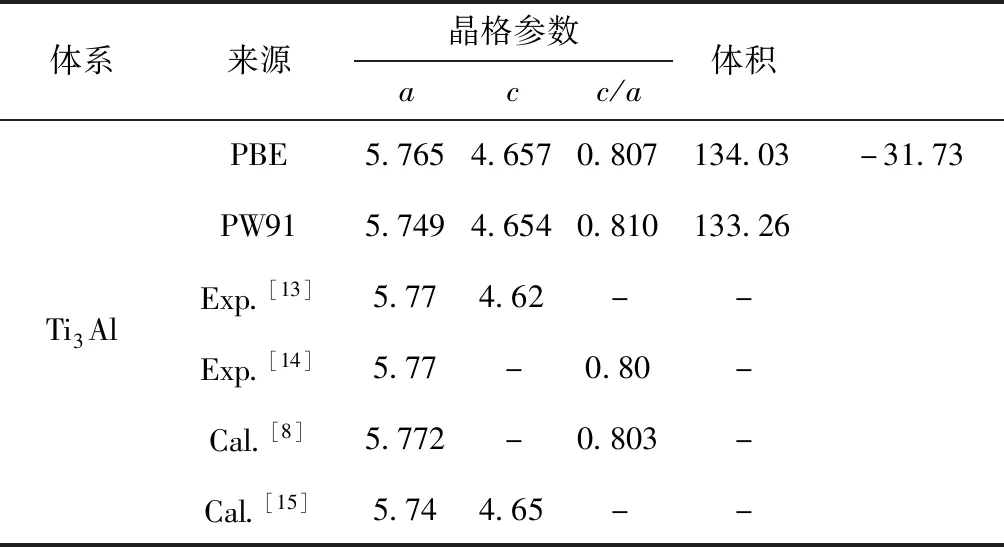
通過對晶格的弛豫計算，得到Ti3Al晶體及其固溶體的平衡結構，計算所得的晶格參數和體積列于表1. 通過對表1中的計算數值與實驗值和其它理論計算值的對比可以發現，采用勢能函數PBE形式的平衡晶格常數誤差更小，均在0.8%以內，故在后續的計算中選擇PBE形式.

表1 Ti3Al的晶格常數(?)和晶胞體積(?3)

Tab.1 The lattice constant (in ?) and the cell volume (in ?3) of Ti3Al

體系來源晶格參數acc/a體積Ti3AlPBE5.7654.6570.807134.03-31.73PW915.7494.6540.810133.26Exp.[13]5.774.62--Exp.[14]5.77-0.80-Cal.[8]5.772-0.803-Cal.[15]5.744.65--

溶質原子取代溶劑原子得到的固溶體的形成焓可以反映其占位傾向，為此計算了固溶體的形成焓(ΔH)，計算公式為：

(1)

Ti3Al晶體及其固溶體中M原子不同占位的形成焓ΔH計算值同樣列于表1，可以看出，純Ti3Al和M原子取代Ti(Al)的固溶體的形成焓均為負值，表明Co、Ni和Ga元素的置換固溶均放熱，可以自發形成，且固溶體結構穩定不易分解. 比較形成焓的數值可以發現，Co和Ni原子占據Ti位時其形成焓較占據Al位小，Co和Ni更傾向于占據Ti；而Ga原子占據Al位時形成焓更小，Ga原子則傾向于占據Al位.

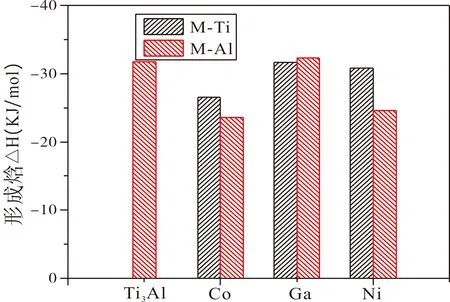
圖2 Ti3Al-M合金體系的形成焓Fig. 2 The enthalpy of formation of the Ti3Al-M system

合金元素M固溶前后Ti3Al晶體的平衡晶格參數a、c及體積見表2，可知，Co、Ni和Ga元素在Ti3Al晶體中固溶均引起了平衡晶格常數和體積變小，原因為3種合金原子的半徑均小于其置換原子，符合置換理論；密排六方結構的Ti3Al晶體c/a值約為0.807，Co、Ni和Ga元素固溶后合金體系的c/a值均發生變化，主要是由于合金原子半徑的不同及成鍵特征的改變引起.

表2 Ti3Al-M(M=Co、Ni和Ga)的晶格常數(?),晶胞體積(?3)

Tab. 2 The lattice constant (in ?) and the cell volume (in ?3) of Ti3Al-M (M=Co, Ni and Ga)

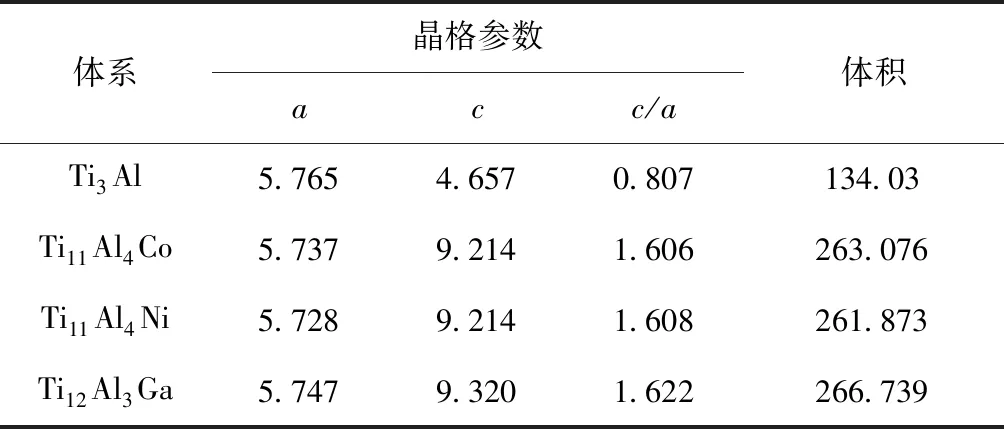
體系晶格參數acc/a體積Ti3Al5.7654.6570.807134.03Ti11Al4Co5.7379.2141.606263.076Ti11Al4Ni5.7289.2141.608261.873Ti12Al3Ga5.7479.3201.622266.739

3.2 電子結構

材料的力學性能與其內部的電荷分布和原子間的成鍵特征等聯系緊密[16]，本文對Ti3Al晶體及其固溶體的電子結構進行了計算分析.

合金體系的總態密度圖(DOS)見圖3，圖中虛線表示費米能級(設置為0)，由圖3可知，在純凈的Ti3Al晶體中，費米能級附近的成鍵峰分布在0.8 eV、-0.5 eV和-1.8 eV附近，其中0.8 eV和-0.5 eV附近的成鍵峰為Ti(d)-Ti(d)鍵，而在-1.8 eV附近的成鍵峰則來自雜化鍵Ti(d)-Al(p). Co、Ni和Ga元素在Ti3Al晶體中固溶均未明顯改變總態密度形狀，說明合金體系的基本物性與純凈Ti3Al保持一致，但可以發現，Co和Ni元素固溶后合金體系在0.8 eV、-0.5 eV和-1.8 eV附近的三個成鍵峰趨于平緩，可以推測Co和Ni元素的固溶能夠削弱三個成鍵峰的電子雜化效應，降低成鍵強度；而Ga元素的固溶后成鍵峰變化不大.

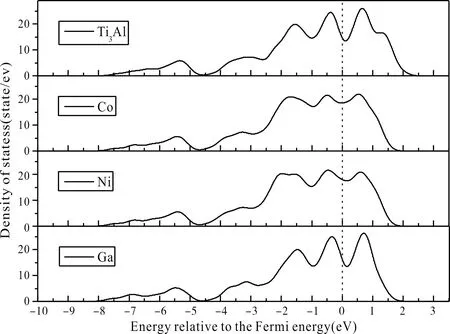
圖3 Ti3Al-M合金體系的態密度(M=Co、Ni和Ga)Fig. 3 The density of states of Ti3Al-M (M=Co, Ni and Ga) alloys

為了更直觀的了解晶體內部的成鍵情況，繪制了Ti3Al晶體固溶前后的差分電荷密度圖，如圖4所示，電荷范圍為-0.1至0.1 e/?3. 由圖4可知，純凈的Ti3Al中，層片間的Ti-Al-Ti原子中Ti原子的周圍出現高密度電荷區域，其中間區域出現少量電荷聚集，表明層片間Ti-Al-Ti之間的成鍵主要為共價鍵和弱金屬鍵；層片間Al-Ti-Al三原子中間區域電荷大量聚集，成鍵主要形式為強金屬鍵；而層內的三個Ti原子附近均出現高密度電荷區域，三者之間的成鍵以強共價鍵形式為主. Co和Ni元素取代Ti原子后，Al-Co(Ni)-Al三原子之間的電荷聚集密度較Al-Ti-Al則明顯降低，表明Co和Ni原子與Al原子之間的金屬鍵強度下降，其中Co元素的作用更加明顯；Ga原子取代Al原子后，Ti-Ga-Ti三原子間成鍵的強度較Ti-Al-Ti變化不大，原因為Ga原子與Al原子具有相同的成鍵電子數.

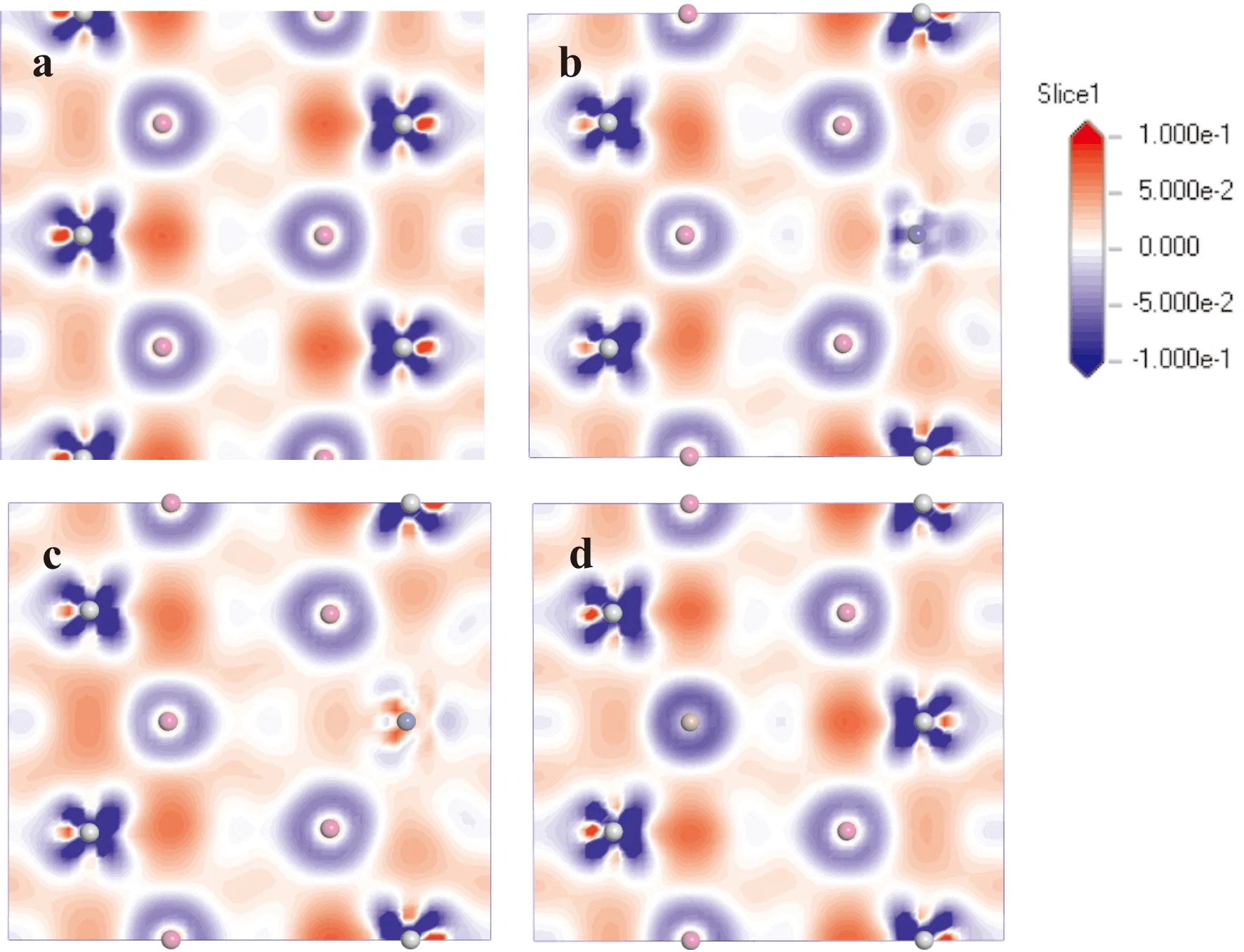
圖4 Ti3Al-M晶體(110)晶面的電荷差分密度(a. pure; b. M= Co; c. M=Ni; d. M=Ga)Fig.4 The charge density density of the (110) plane on the Ti3Al-M crystal(a. pure; b. M= Co; c. M=Ni; d. M=Ga)

3.3 彈性性能

通過晶體的彈性常數的計算可以得到表征材料宏觀力學性能的體模量、剪切模量及楊氏模量等性能指標[17]，本文計算了Ti3Al晶體固溶前后的彈性常數列于表3. 合金原子的置換引起Ti3Al晶體的對稱性改變，對于Ga元素取代Al原子后晶體仍為六方晶系，而Co和Ni原子取代Ti原子后晶體為正交晶系.

對于六方晶系和正交晶系，利用Voigt-Reuss-Hill方法可以通過其彈性常數計算得到體模量B、剪切模量G、楊氏模量E和泊松比υ，計算公式如下：

(2)

(3)

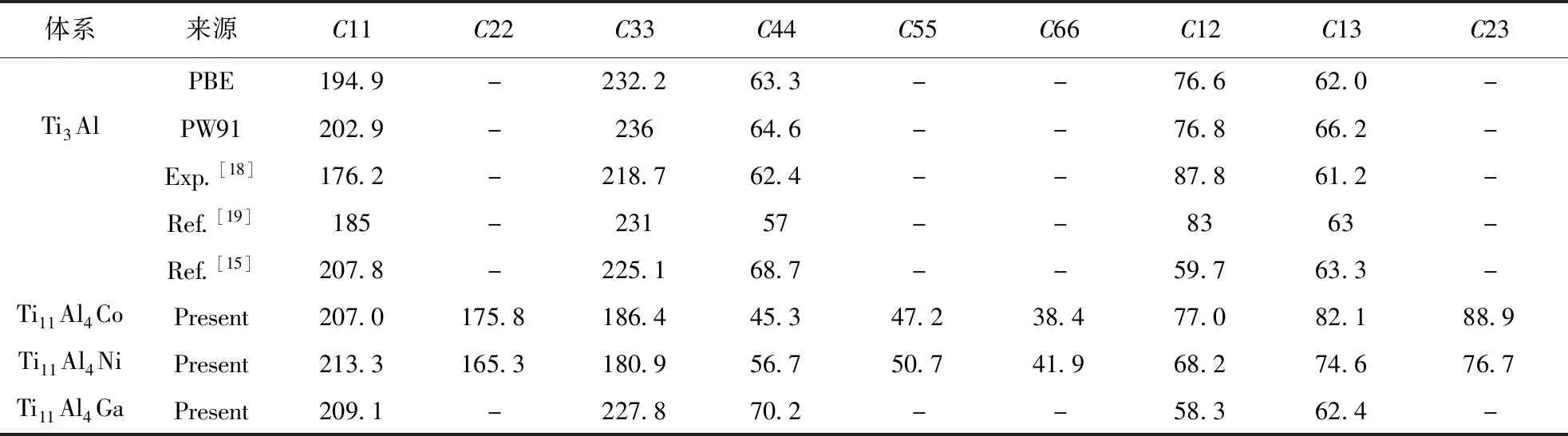
表3 Ti3Al-M晶體彈性常數(GPa)(M=Co、Ni和Ga)

(4)

(5)

(6)

對于六方晶系：

(7)

BR=C2/M

(8)

(9)

M=C11+C12+2C33-4C13

(10)

(11)

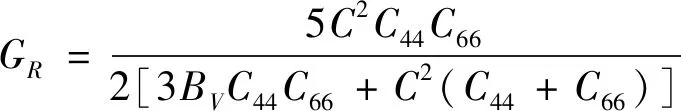
(12)

C66=(C11-C12)/2

(13)

對于正交晶系：

(14)

C33+3(C44+C55+C66)]

(15)

C23(C12C23-C23C11)+C33(C11C22-C122)

(16)

(17)

Δ=C11(C22+C33-2C23)+C22(C33-2C13)-

2C33C12+C12(2C23-C12)+

C13(2C12-C13)+C23(2C13-C23)

(18)

Δ1=C11(C22+C33+C23)+

C22(C33+C13)+C33C12-C12(C23+C12)-

C13(C12+C13)-C23(C13+C23)

(19)

合金體系的相關計算結果列于表4，可以看出：Co元素固溶后合金體系的體模量B增大，則合金體系的抗體積變形能力提升，而Ni和Ga元素固溶則導致體模量降低，其中Ni元素的降低作用更加明顯；對于剪切模量G，Ga元素的提升效果明顯，Co和Ni元素則降低作用明顯；3種合金元素對晶體的楊氏模量E的影響與其對剪切模量G的影響相似，即Ga元素的固溶提升剛度，Co和Ni元素則降低剛度. 一般來說，材料的楊氏模量E和剪切模量G越大，其硬度越大，由表4可知，Ga元素固溶后合金體系的硬度將增大，而Co和Ni元素固溶將顯著降低材料的硬度. 由于材料的彈性模量是由其晶體內原子間成鍵狀態決定，由上節的電子結構分析可知，Co和Ni元素可以減弱電子雜化效應，成鍵的強度下降，故材料的硬度下降.

通過晶體的模量數值可以預測其本征塑性，常用的衡量指標有G/B和泊松比υ兩種[20, 21]. 對于G/B的數值越小則材料的延性越好，本征塑性越高，反之，其數值越大材料的脆性越大，本征塑性越差，常用的區分材料延性和脆性的分界值為0.57. 對于純凈的Ti3Al晶體，其G/B值約為0.57，其處于延性和脆性的分界值，本征塑性較低. Co和Ni元素固溶后，Ti11Al4Co和Ti11Al4Ni晶體的G/B值分別下降為0.398和0.470，表明Co和Ni元素固溶后材料呈延性，Co和Ni元素合金化有利于提高合金體系的本征塑性. 對于Ga元素固溶后晶體的G/B值增大明顯，合金體系的脆性更加明顯. 泊松比υ的數值越大，材料的塑性越好. 對于純凈的Ti3Al晶體，其泊松比υ計算結果約為0.260，與實驗結果吻合較好. Co和Ni元素固溶后合金體系的泊松比均增大，晶體的塑性有所提高，其中Co元素固溶后晶體的泊松比數值增大效果更加明顯，其值達到0.324，表明Ti11Al4Co晶體的塑性較純凈Ti3Al晶體提高顯著；而Ti11Al4Ga的泊松比數值下降較多，Ga元素固溶將降低晶體的塑性.

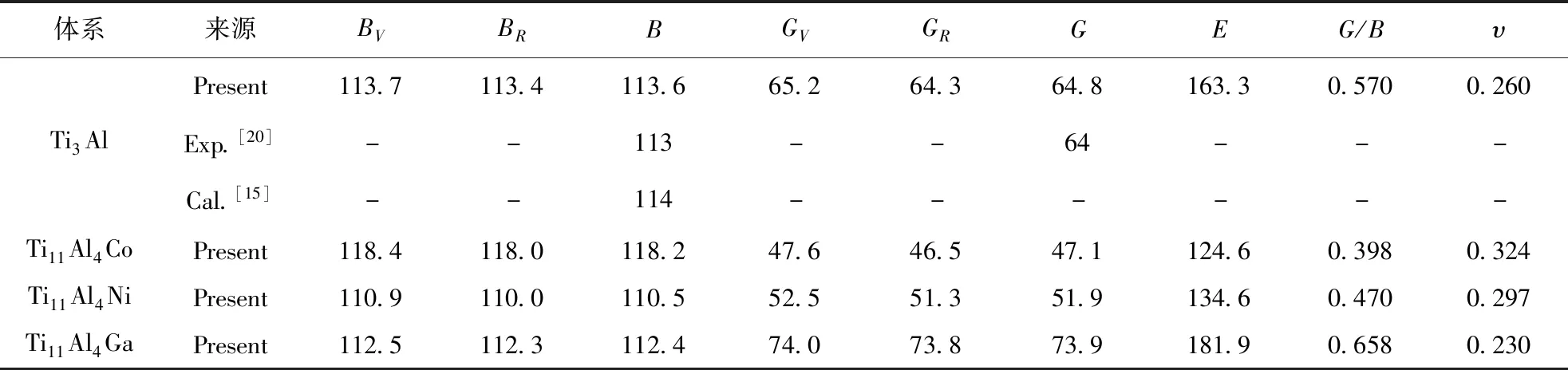
表4 Ti3Al-M晶體的模量(GPa)、G/B和泊松比

3.4 德拜溫度

德拜溫度ΘD與固體材料中共價鍵強度關系密切，共價鍵的成鍵越強越高，德拜溫度的數值越大[21]. 利用德拜準諧模型，晶體的德拜溫度可以由晶體的彈性系數進行估算.

計算所得的德拜溫度列于表5，可知，Co、Ni和Ga元素后晶體的德拜溫度均發生變化，其中Co和Ni元素導致晶體的德拜溫度由純凈Ti3Al晶體的506 K下降為430 K和450 K，而Ga元素固溶后晶體的德拜溫度上升為523 K，由德拜溫度的計算結果可以推測晶體內部成鍵的共價性由強到弱以此為：Ti11Al4Ga、Ti3Al、Ti11Al4Ni和Ti11Al4Co，推測結果為電子結構分析結果一致. 對比彈性模量計算結果可以發現，Ti11Al4Co和Ti11Al4Ni德拜溫度下降主要原因為其剪切模量和楊氏模量均較純凈Ti3Al降低.

表5 Ti3Al-M合金的德拜溫度ΘD(K)

Tab. 5 The Debye temperature of (in K) of the Ti3Al-M alloys

晶體Ti3AlTi11Al4CoTi11Al4GaTi11Al4Ni德拜溫度506430523450

4 結 論

采用第一性原理對合金元素Co、Ni和Ga在Do19-Ti3Al的固溶體進行研究，通過對晶體結構、電子結構和彈性常數的分析得出以下結論：

1)Ga元素傾向于置換Ti3Al晶體中Al原子，Co和Ni元素則更傾向于置換Ti原子；

2)Ga元素固溶后與Ti原子成鍵強度升高，而Co和Ni元素原子與Al原子之間的金屬鍵強度下降.

3)Ga元素固溶強化效果顯著，晶體的強度和硬度均提升；Co和Ni元素固溶導致合金體系的塑性顯著提升，其中Co元素的效果更佳.