防空制導炮彈的指令控制模式分析

姚鴻鶴,盧發興,許俊飛

(海軍工程大學兵器工程學院,湖北 武漢 430033)

指令制導彈上設備少、重量輕的優點使其成為用于近程防空的防空制導炮彈優先選擇的制導方式[1-3],根據控制指令形成方式的不同,指令制導又可以分為多種指令控制模式,不同的模式,其制導系統的組成有差異,對系統各環節的精度要求也不同,因此開展指令控制模式的研究是一個亟待解決的問題,這對防空制導炮彈指令控制模式的選擇具有重要意義。

制導精度是影響指令控制模式選擇的重要因素,而制導精度主要與跟蹤雷達、慣導器件、數據鏈等硬件設備的精度緊密相關。近年來,國內外學者對相關問題做了如下研究:文獻[4]對精密跟蹤設備的跟蹤精度進行了建模分析,介紹了國內外跟蹤雷達系統的性能指標;文獻[5]研究了指令制導系統中,目標、導彈跟蹤設備的系統誤差和隨機誤差,并對其進行了仿真分析;文獻[6]針對傳統的指令制導方式,對指令的制導回路以及指令的形成和控制原理進行了研究;文獻[7-8]對制導系統中各誤差源的隨機誤差進行了建模,并運用伴隨法分析了各誤差對制導系統制導精度的影響;文獻[9-10]分別研究了角速度零位誤差和隨機風誤差對比例導引制導率制導精度的影響,并對復雜的制導回路進行了分析;文獻[11]以某型導彈為例,分析了目標跟蹤誤差和慣導設備誤差對導彈制導精度的影響,并提出了一種分析導彈制導系統硬件設備精度要求的方法。可見上述文獻主要針對制導系統誤差、制導精度以及制導系統硬件設備的精度開展研究,但從指令控制模式選擇的角度,對在不同條件下哪種模式更為合適的問題并未做深入研究。

針對以上問題,本文對指令控制模式中涉及的誤差進行了建模,并運用蒙特卡洛打靶法分析了不同模式中各誤差對制導精度的影響,初步得到了各指令控制模式的適用條件。

1 指令控制模式分析

指令制導系統是以防空制導炮彈為控制對象的閉環回路,圖1給出了指令制導回路[6]的框圖。

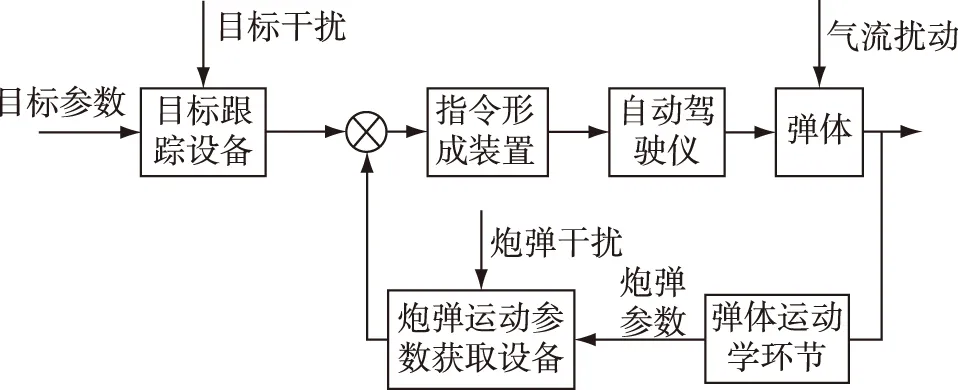
圖1 指令制導回路

根據炮彈運動參數的獲取方式以及指令形成裝置的載體的不同,采用指令制導的防空制導炮彈的指令控制模式一般分為6種,如圖2所示。

記6種指令控制模式分別為Ⅰ型、Ⅱ型、Ⅲ型、Ⅳ型、Ⅴ型、Ⅵ型。其中，Ⅰ型、Ⅱ型、Ⅲ型的指令形成裝置安裝在彈體上,Ⅳ型、Ⅴ型、Ⅵ型是在艦面制導站形成控制指令,然后由指令發射裝置向炮彈發送指令來控制炮彈飛行。但對于炮彈運動參數的獲取,Ⅰ型和Ⅳ型通過融合炮彈慣導設備和炮彈跟蹤設備提供的炮彈運動參數來得到;Ⅱ型和Ⅴ型通過炮彈慣導設備提供的炮彈運動參數來得到;Ⅲ型和Ⅵ型則通過炮彈跟蹤設備提供的炮彈運動參數來得到。

圖2 防空制導炮彈指令控制模式

2 誤差模型

誤差是影響防空制導炮彈制導精度的主要影響因素,在炮彈制導過程中,誤差源主要有目標跟蹤設備誤差、炮彈運動參數獲取設備誤差、指令延遲誤差、起控點散布誤差和大氣擾動誤差等[3,11]。為方便分析問題,本文只分析6種指令控制模式涉及的誤差,包括目標跟蹤誤差、炮彈定位誤差、慣導設備誤差、起控點散布誤差及延時誤差,且在發射坐標系下建立誤差模型。

2.1 目標觀測誤差模型

現役的武器裝備中,雷達是主要的觀測設備,首先建立發射坐標系OXYZ,如圖3所示,O為炮彈的發射原點,OX軸在水平面內,指向水平面內某一指定方向,OY軸垂直于當地水平面向上,OZ與OX、OY軸構成右手系。

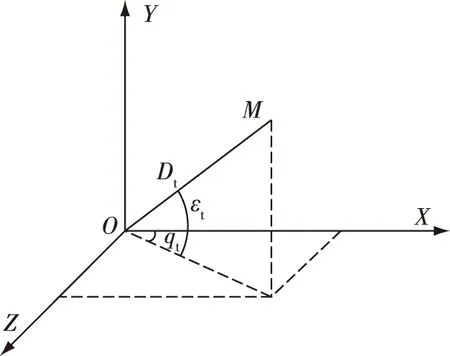
圖3 球坐標向發射坐標系轉換

圖3中,M點為目標,Dt、εt、qt為目標的距離、高低角、方位角。

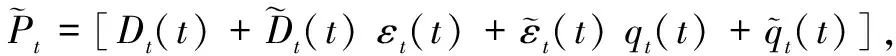
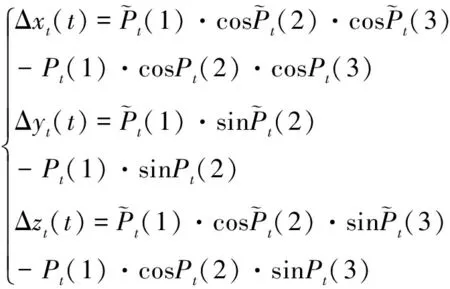
(1)

2.2 慣導設備的誤差模型

慣導設備的定位誤差主要是陀螺和加速度計的漂移造成的,陀螺和加速度計的漂移又可分為常值漂移和隨機漂移[13]。

對于常值漂移,可以用誤差累計的速率來表征慣導設備定位性能的優劣[11],則慣導設備的常值漂移造成的定位誤差δg=[ΔgxΔgyΔgz]可表示為

(2)

對于隨機漂移,假設漂移量δn=[ΔnxΔnyΔnx]為平穩隨機過程,其特性可以用一維指數型的自相關函數來表示[7]

(3)

式中,σni為隨機漂移造成的誤差均方差;pi為自相關系數。

有色噪聲可以用一個功率譜為φni的高斯白噪聲通過一個傳遞函數為Hi(s)的成形濾波器來表示,經過數學推導可得[10]

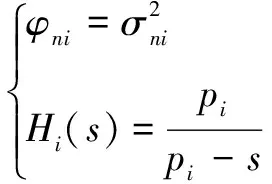
(4)

將常值漂移和隨機漂移用方和根法合成得到慣導設備誤差δgn,有

(5)

2.3 起控點散布誤差模型

起控點散布誤差主要是由于初始段擾動導致的[14],一般情況下,可以用服從正態分布的隨機變量來表示,即

(6)

式中,δr為起控點散布誤差;μ為起控點散布誤差的數學期望;σr為起控點散布誤差的均方差;xj為正態分布的隨機數,即xj～N(0,1)。

2.4 延時模型

制導系統中的延時環節是不可避免存在的,它們也是影響防空制導炮彈制導精度的重要因素[15],在本文分析的這6種制導模式中,涉及的主要延時有

1)制導指令由艦面制導站形成,然后發送到彈上而產生的指令傳輸延時T1;

2)炮彈的慣導設備測得的炮彈運動參數需要發送到艦面制導站而產生的數據鏈傳輸延時T2;

3)炮彈和目標跟蹤設備測得的運動參數需要發送到彈上而產生的數據鏈傳輸延時T3、T4。

假設艦面制導站向彈體發送的制導指令為N,慣導設備、炮彈和目標跟蹤設備提供的炮彈運動參數分別為M1、M2、M3(包括炮彈位置、速度等運動要素),建立延時模型,有

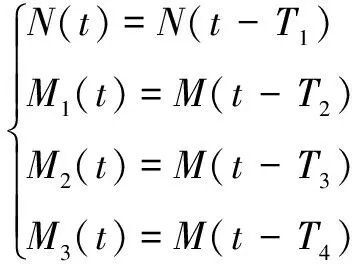
(7)

各指令控制模式涉及的延時如表1所示。

表1 不同指令控制模式的延時

2.5 炮彈定位誤差模型

炮彈主要通過炮彈跟蹤設備、慣導設備或兩者信息融合實現定位,要建立炮彈定位誤差模型,首先要對炮彈跟蹤設備的觀測誤差進行建模,其原理與目標跟蹤設備相同,這里不在贅述,直接給出炮彈跟蹤設備的觀測誤差模型,有

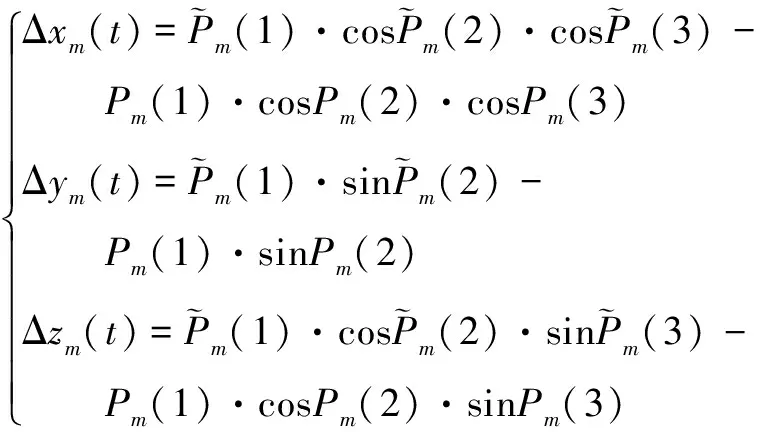
(8)

(9)

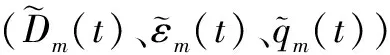
其次,建立慣導設備誤差模型,如上文所示。

最后,針對六種指令控制模式中炮彈定位的特點建立炮彈定位誤差模型。記δp為炮彈定位誤差,I型和IV型中需要根據誤差融合模型[16]建立炮彈定位誤差模型,有

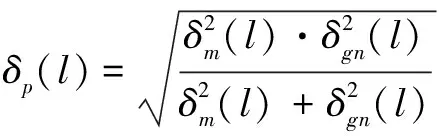
(10)

式中,l=1,2,3。

Ⅱ型和Ⅴ型中炮彈定位誤差模型與慣導設備的誤差模型相同,即

δp=δgn

(11)

Ⅲ型和Ⅵ型中炮彈定位誤差模型與炮彈跟蹤設備的誤差模型相同,即

δp=δm

(12)

3 誤差對制導精度影響模型

蒙特卡洛法(Monte Carlo)、協方差分析函數描述法(CADET)、統計線性化伴隨法(SLAM)是分析制導彈藥制導精度的主要方法[17]。Monte Carlo法是一種統計實驗法,它利用計算機數值模擬來代替具體實驗,通過多次模擬打靶仿真研究系統統計意義下的特性,因此相對于其他兩種方法,Monte Carlo法的計算結果更為穩定和精確[17]。因此本文應用蒙特卡洛打靶法建立誤差對制導精度的影響模型。基本步驟如下:

1)建立彈道仿真模型

防空制導炮彈的彈道方程包括動力學方程、質心運動學方程、繞質心轉動的剛體運動方程、坐標系轉換方程及導引方程[18],假設炮彈采用比例導引制導律[10],其外彈道建模詳見文獻[18],文中不在贅述。

2)確定炮彈飛行過程中的隨機干擾因素,確定其分布律

影響炮彈制導精度的隨機干擾主要有三類:

第一類是炮彈結構參數誤差,主要包括質量偏差Δm和質心偏差Δc;

第二類是發射過程中的干擾。主要包括發射仰角干擾Δε、發射方位角干擾Δβ、發射速度干擾ΔV、彈道傾角干擾Δθ、彈道偏角干擾Δψv、俯仰角干擾Δ?、偏航角干擾Δψ、阻力系數干擾ΔCx、升力系數干擾ΔCy、側力系數干擾ΔCz等;第三類是隨機風的影響,隨機風主要為彈道橫風干擾ΔWz和彈道縱風干擾ΔWx。

以上隨機干擾因素均服從正態分布,其變化范圍如表2所示[14]。

表2 隨機干擾變化范圍

其中，第一類和第二類可通過調整模型參數和改變仿真初值來實現,但對于第三類隨機干擾,首先將隨機風與炮彈速度V合成得到炮彈的相對速度Vr,設炮彈速度在發射坐標系為V=(Vx,Vy,Vz),隨機風速在發射坐標系為W=(ΔWx,0,ΔWz),則

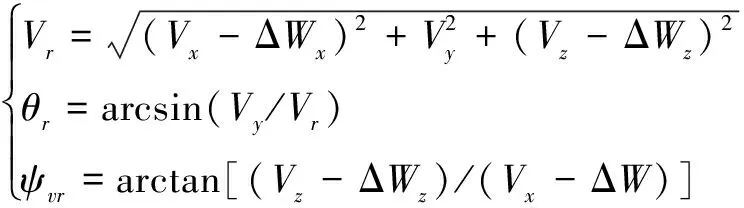
(13)

式中,θr為相對彈道傾角;ψvr為相對彈道偏角。

然后利用Vr、θr、ψvr代替炮彈速度V、彈道傾角θ、彈道偏角ψv進行彈道仿真。

3)將隨機干擾和第2節中的誤差加到炮彈六自由度彈道仿真模型中(對于起控點散布誤差,將其加到炮彈的起控距離上;對于延時誤差,利用Simulink工具箱中的Variable Time Delay模塊來實現),進行n次打靶實驗,得到炮彈在發射坐標系的彈著點(x,y,z)樣本(xk,yk,zk)和制導精度zm樣本zmk。其中zmk的計算公式為

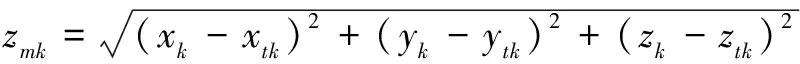
(14)

式中,(xtk,ytk,ztk)為仿真結束時目標在發射坐標系的位置,k=1,2,…n。

4)對蒙特卡洛打靶結果進行統計分析,計算zmk的數學期望,并將其作為炮彈的制導精度,即

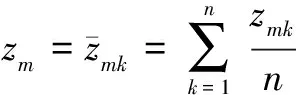
(15)

4 仿真分析

假設利用防空制導炮彈打擊運動目標,且目標做勻速直線運動,初始位置為(15 000 m,20 m,0 m),速度為(-300 m/s,10 m/s,10 m/s),仿真步長取0.02 s,將每一時刻炮彈和目標的理想軌跡點作為其真實位置,仿真初始條件如表3所示[18]。

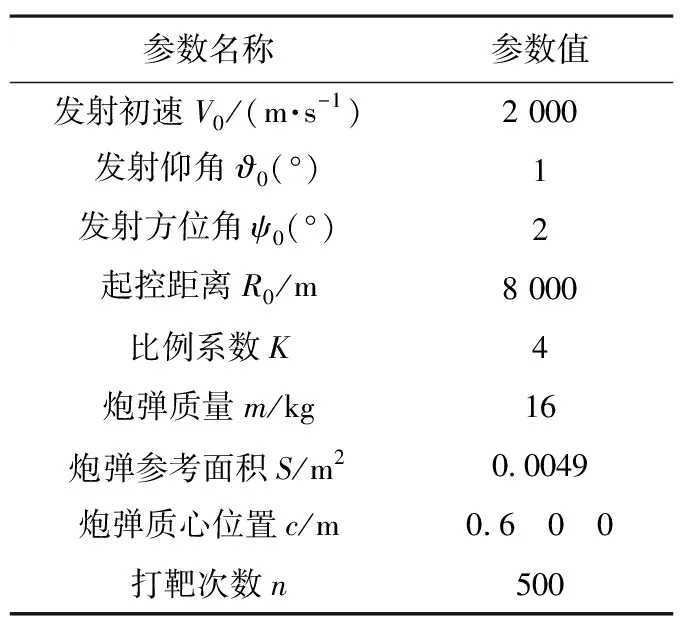
表3 仿真初始參數

表4 誤差參數仿真初值

把各參數的中間取值定為基準值,即在每次計算中,參數中最多只有一個誤差因素的初值取非基準值,而其他的參數均取基準值。

1)以Ⅰ型為例,當各參數取基準值時,炮彈彈著點分布情況如圖4所示,制導精度分布圖如圖5所示;取制導時間T=12 s,Ⅰ～Ⅵ型制導精度隨制導時間的變化曲線如圖6所示。

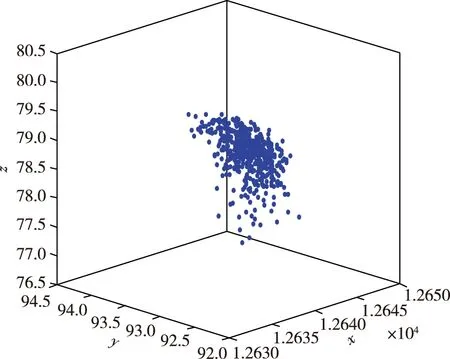
圖4 炮彈彈著點散布三維圖

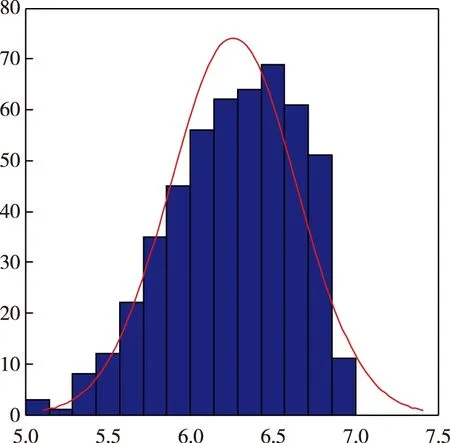
圖5 制導精度分布圖

圖6 炮彈位置誤差曲線

2)在給定初值條件下計算制導精度zm,結果如表5-7所示。

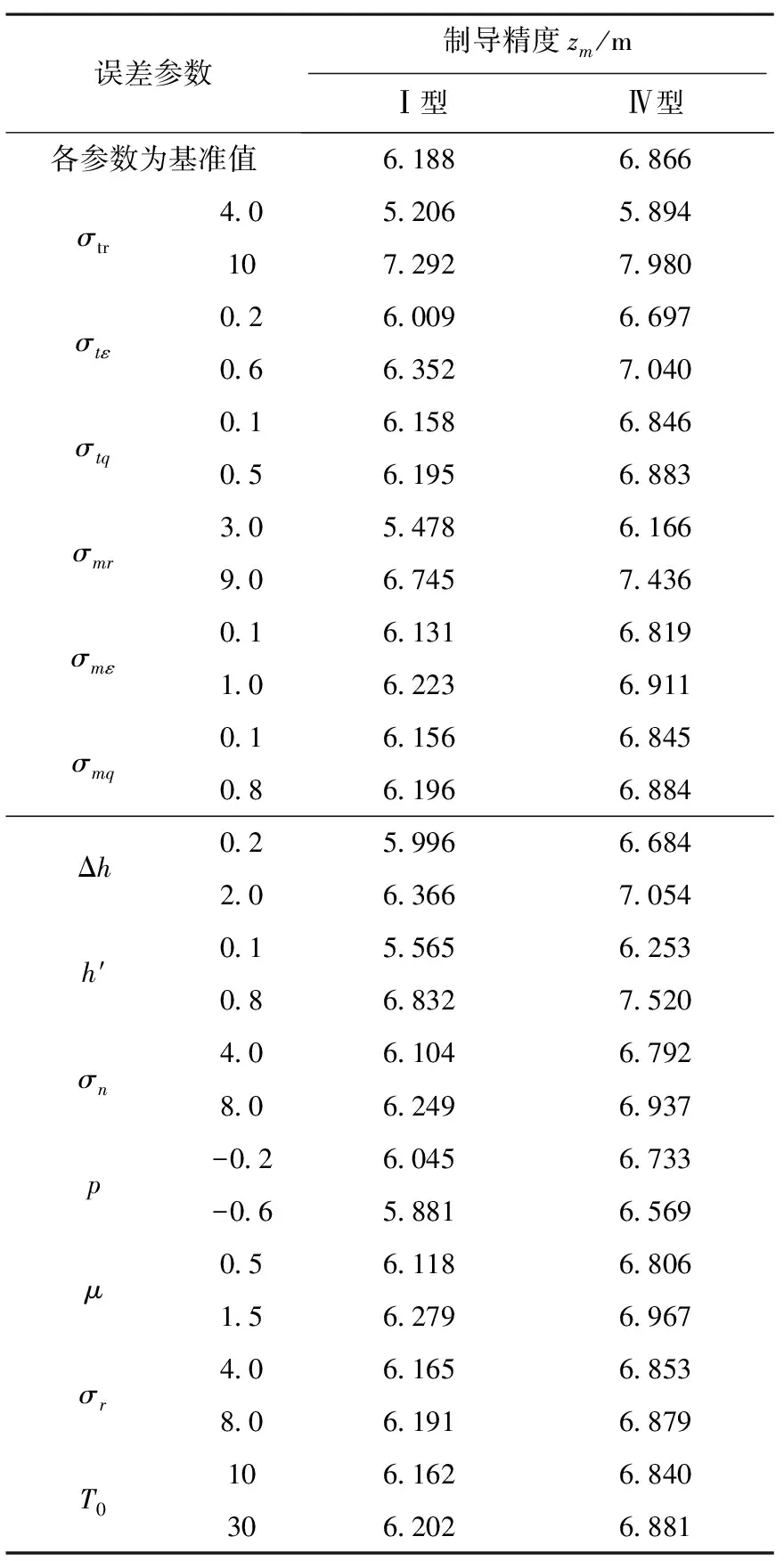
表5 各誤差參數對制導精度的影響(Ⅰ型和Ⅳ型)

表6 各誤差參數對制導精度的影響(Ⅱ型和Ⅴ型)

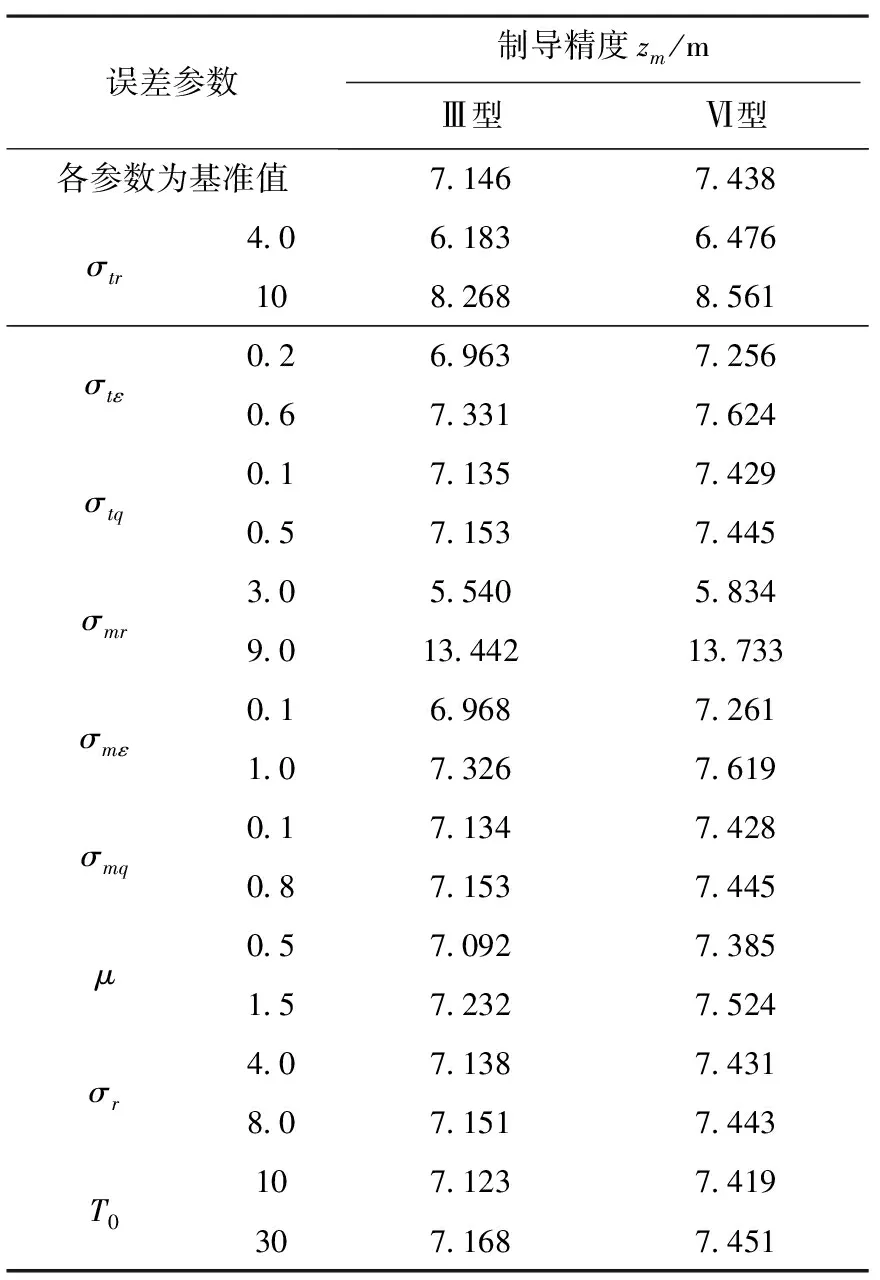
表7 各誤差參數對制導精度的影響(Ⅲ型和Ⅵ型)

根據仿真結果可以得到以下結論:

1)蒙特卡洛打靶結果表明,炮彈彈著點隨機分布,且無異常落點,制導精度近似滿足正態分布,從而驗證了本文采用蒙特卡洛打靶法建立的誤差對制導精度影響模型的正確性;

2)在6種指令控制模式中,炮彈位置誤差隨制導時間的增大而增大,且任意一個誤差參數增大(減小),炮彈位置誤差也隨之增大(減小);

3)對6種不同的指令控制模式比較可得出,延時對指令在艦面形成的Ⅳ型、Ⅴ型、Ⅵ型影響較大,尤其是對Ⅳ型、V型,這是由于在Ⅳ型和Ⅴ型中,既存在指令傳輸延時,又存在炮彈和目標運動信息的傳輸延時。因此在數據鏈性能較好時,可優先考慮采用Ⅳ型、Ⅴ型、Ⅵ型,較差時,則應優先考慮采用Ⅰ型、Ⅱ型、Ⅲ型;

4)當炮彈跟蹤設備精度較低或慣導設備的漂移較大時,Ⅰ型和Ⅳ型的制導精度明顯高于Ⅱ型、Ⅲ型、Ⅴ型和Ⅵ型,即當炮彈采用跟蹤雷達和慣導設備融合定位的方式時,制導精度會明顯提高。但當炮彈跟蹤設備精度較高或慣導設備的漂移較小時,I型和Ⅳ型制導精度提高的相對較小,因此從成本考慮,此時Ⅱ型、Ⅲ型、Ⅴ型和Ⅵ型較為合適。

5 結束語

本文從制導精度出發,對防空制導炮彈的6種不同的指令控制模式進行了分析。根據指令控制模式的特點,建立了誤差分析模型,并基于典型的誤差參數,通過仿真詳細研究了6種指令控制模式下誤差對制導精度的影響,初步得到了各指令控制模式的適用情況。該分析方法能為不同條件下防空制導炮彈指令控制模式的選擇提供依據,具有一定的工程應用價值。