基于區間相離度的異步航跡抗差關聯算法
周 威,衣 曉,楊衛國
(海軍航空大學,山東 煙臺 264001)
在雷達組網系統中,由于雷達開機的異步以及雷達采樣周期不同,導致航跡是異步的;同時系統誤差也會對算法性能造成一定程度的影響。因此,研究在雷達異步,帶有系統誤差的情況下,如何進行精準的航跡關聯是有必要的[1-4]。
目前,異步航跡關聯的一般算法是需要將異步航跡經過時域配準到同一時刻,再采用經典的航跡關聯算法進行關聯。文獻[5]提出了基于最小二乘法的異步航跡關聯算法;文獻[6]提出了通過構造偽點跡來實現航跡同步化的算法;文獻[7]提出了一種改進蟻群算法。上述的算法均是通過時域配準得到估計值,而由于估計而帶來的誤差在這一過程中是無法估量的。文獻[8]提出了一種基于OSPA距離的算法,但只能解決航跡生命周期不同情況時的異步航跡關聯問題。文獻[9]提出了一種無須配準的基于區實序列的異步航跡關聯算法,但需要預知雷達采樣頻率比。文獻[10-11]提出了將系統誤差對航跡的影響看成是航跡的旋轉和平移,利用傅里葉變換理論對航跡進行補償,進而實現航跡關聯。文獻[12]將系統誤差對航跡的影響用灰區域來描述,并提出了一種基于區間相離度的航跡灰關聯算法。
針對雷達采樣異步、系統誤差的影響等問題,本文以灰關聯理論為基礎,綜合分析目標機動的性能,提出了一種無須時域配準,抗系統誤差的航跡灰關聯算法。
1 模型建立
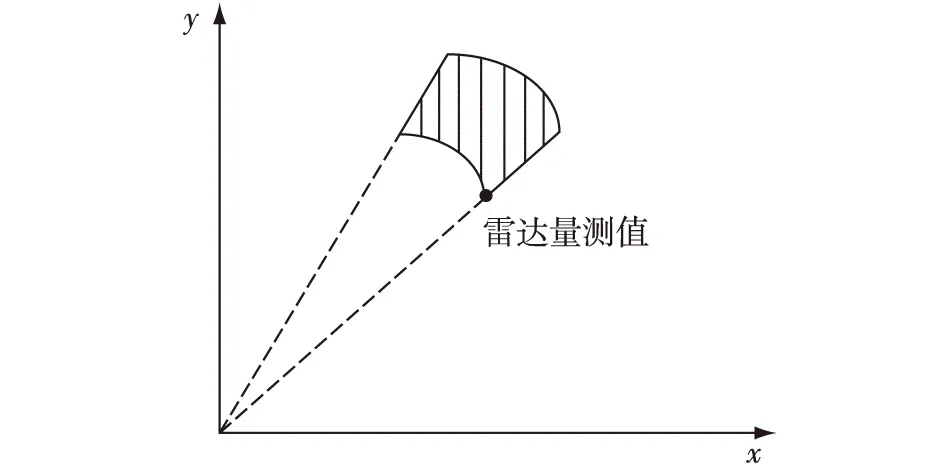
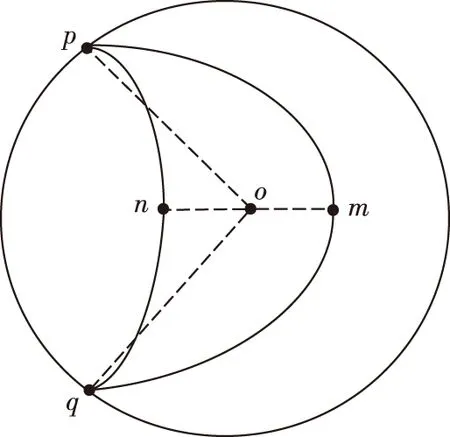
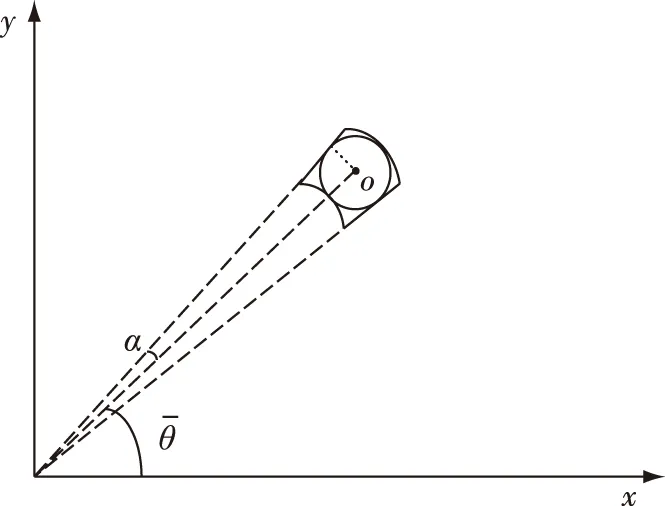
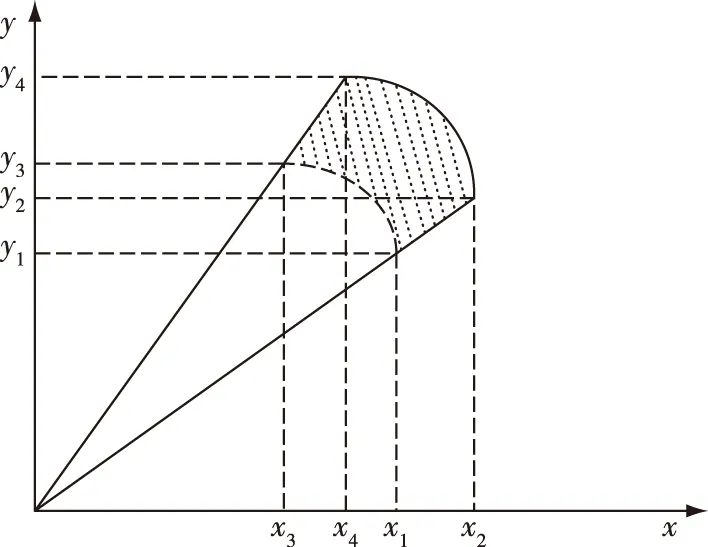
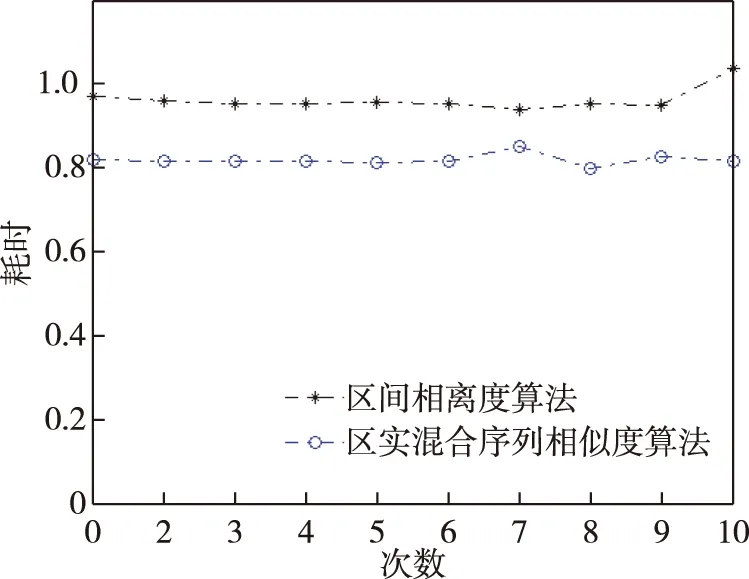
假設異地配置的兩部2D雷達A、B同時對目標區域進行監測。以雷達A為原點建立笛卡爾坐標系,雷達B的坐標為(xs,0)。雷達A的探測周期為Ta,雷達B的探測周期為Tb,且Ta 雷達A探測目標區域形成的航跡集合為Γb(k),即 (1) 雷達B的目標航跡集合為Γb(h), (2) 圖1 航跡異步示意圖 以探測周期較大的雷達B的量測值為基準,推算出雷達A的目標航跡量測值在雷達B探測時刻的目標位置區域。目標在運動時,受到機動性能的限制,可以推斷目標位置下一時刻可能存在的區域。 飛機轉彎過程較為復雜,本文簡化考慮飛機轉彎過程,大體上飛機轉彎的飛行狀態可分為三種,依次為:進入狀態、勻速盤旋狀態、改出狀態。 分析飛機機動時受力情況,如圖2所示。 圖2 飛機受力示意圖 圖2中,L是飛機飛行的升力,W是飛機本身的重力,γ是飛機升力與地面垂直線的夾角。 飛機處于勻速盤旋時,此時飛機的受力處于平衡狀態,如式(3)所示: (3) 式中,P是飛機推力,D是飛機阻力,v是目標運動速度,r是目標轉彎半徑,m是目標重量。 飛機油門產生的推力與阻力、飛機本身重力與拉力在垂直線上的分力相互抵消,僅剩拉力水平方向的分力為飛機轉彎提供向心力。此時飛機做勻速圓周運動。 飛機處于轉彎進入狀態時,飛機增大油門,速度增大,同時飛行坡度不斷增大,隨之升力與垂直線的角度不斷增大,提供飛機轉彎的向心力不斷增大。此時飛機飛行速度不斷變大,飛機轉彎半徑不斷減小。 飛機處于轉彎改出狀態時,飛機減小油門,速度減小,同時飛行坡度不斷減小,隨之升力與垂直線的角度不斷減小,飛機轉彎的向心力不斷減。此時飛機飛行速度不斷減小,飛機轉彎半徑不斷增大。 在T時刻,雷達B探測到目標,而雷達A探測的時刻距T最近為T-Δt時刻。根據目標本身性能,推斷T時刻雷達A探測目標位置區域。在這Δt時間內,目標運動可能處于勻速飛行、加速、減速、轉彎等情況。如圖3所示。 圖3 目標位置區域示意圖 圖3中,m為飛機以最大加速度直線運動到達的點,n為飛機以最大減速度直線運動到達的點;而p、q為飛機已經處于穩定狀態,以最小轉彎半徑轉彎所能到達的點。 邊界pmq上的點是飛機處于進入狀態,馬上進入平穩盤旋狀態所到達的位置,處于進入狀態時間越長,越靠近m點;邊界pnq上的點是飛機脫離平穩盤旋狀態,已經處于改出狀態所到達的位置,處于改出狀態時間越長,越靠近n點。 飛機處于進入狀態時,飛機的速度不斷增大,并且提供轉彎的升力分支還比較小,因此飛行路線必定在飛機直線行駛路線的附近,如圖3中線fs。 當飛機處于改出狀態時,飛機的速度減小。因此其運動軌跡與處于穩定轉彎狀態下的運動軌跡相比,必定在最小轉彎半徑路徑以內,如圖3中線fh。 (4) (5) 根據目標機動性能以及雷達A的航跡集合Γa(k)與雷達B的航跡集合Γb(h),推算出同一時刻雷達A探測目標的灰區域集合Γa(h),即 (6) 雷達在探測目標時,存在系統誤差以及隨機誤差等多種誤差。實際應用中系統誤差的范圍是可知的,可以通過量測值和系統誤差反推出目標真實位置存在的區域。 假設雷達B的測距和測角系統誤差范圍為(0,Δrb),(0,Δθb),量測值距離和角度分別為rb、θb。 (7) 由此可以反推出雷達B量測值的目標真實位置灰區域,即 (8) 目標真實位置灰區域如圖4所示。 圖4 目標真實位置灰區域示意圖 (9) (10) (11) 覆蓋圓灰區域如圖5所示。 圖5 目標位置區域覆蓋圓示意圖 根據覆蓋圓灰區域相對雷達A的位置以及自身的形狀,將其放大表示為扇形區域: (12) (13) (14) (15) 放大扇形灰區域如圖6所示。 圖6 扇形灰區域示意圖 假設雷達A的測距、測角系統誤差范圍為(0,Δra)、(0,Δθa)。根據目標位置灰區域和雷達系統誤差范圍,可以推算出目標真實位置灰區域。 (16) 二度放大灰區域如圖7所示。 圖7 二度放大灰區域示意圖 圖7中,陰影區域表示目標真實位置灰區域,T時刻目標的真實位置必定在該灰區域內。 航跡異步和系統誤差對算法性能的影響隨著時間的推移不斷擴大。對此,以基準航跡為準,根據本文上述對目標機動性能的分析,推算下一時刻雷達探測得到的目標位置所在區域;然后根據系統誤差對航跡的影響,將航跡推算得到系統誤差灰區域。通過這種方法減小由于時域配準而帶來的誤差以及由于系統誤差造成的航跡位置偏移給算法帶來的影響。 以雷達B的航跡集合Γb(h)為基準,根據雷達A的航跡集合Γa(k),推算出航跡Γa(k)在航跡Γb(h)時刻的目標所在位置灰區域,即將Γa(k)轉化為Γa(h)。 按上文算法,推算出航跡集合Γa(h)、Γb(h)的目標真實位置所在區域,并將目標真實位置灰區域分解到x、y軸上,轉化為兩個區間(min(Xa),max(Xa))、(min(Ya),max(Ya))。如圖8所示。 圖8 灰區域分解示意圖 雷達A:Γa(h)經過二度放大得到的灰區域四個點坐標為 Xa=Ra·Φa1、Ya=Ra·Φa2 (17) 雷達B灰區域分解與雷達A灰區域分解相似,這里不再贅述。 從雷達B集合Γb(h)中選取一條航跡作為待識別航跡,將雷達A的航跡集合Γa(h)作為已知航跡,判斷航跡集合Γa(h)中哪條航跡和待識別航跡來自同一目標。 將k時刻的來自雷達B的一條待識別航跡與雷達A的所有航跡組成決策矩陣Ψ,即 (18) 式中(min(Xb),max(Xb))j、(min(Ya),max(Ya))j為雷達B的第j條待識別航跡,(min(Xa),max(Xa))、(min(Yb),max(Yb))為雷達A的所有航跡集合,即已知航跡。 將第Ns+1行與前Ns比較,分別求其航跡灰關聯度,即 (19) (20) (21) 區間相離度表示兩個區間的相對距離遠近,區間相離度越小,兩個灰區域越近,同時兩個航跡點來自同一目標的概率也就越大。ρ為分辨系數,這里取0.5。 設閾值σ=0.97,若航跡對關聯正確且γij≥σ,則認為關聯正確;若航跡對關聯正確且γij<σ,則認為漏關聯;否則認為關聯錯誤。 為了方便評估算法的性能,引入航跡正確關聯率,即 (22) 式中N是每次仿真的目標數,M是蒙特卡洛仿真次數,Eci(k)是每次仿真正確關聯的航跡對數。 雷達A的坐標為(0,0),雷達B的坐標為(100 km,0)。假設目標的起始速度方向和大小分別為0~2 πrad、200~400 m/s,起始區域位為40 km×40 km的矩形區域,目標批次為20。假設目標最小轉彎半徑為700 m,最大轉彎角速度為 21.7°/s,最小最大加速度均為5 m/s2。 算法性能受很多因素影響,包括密集度、系統誤差、距離、方位角等方面,下面就上述因素對本文算法與文獻[9]算法進行比較分析。 場景一:雷達A的測距系統誤差、測角系統誤差為100 m、0.5×π/180 rad,雷達B的測距系統誤差、測角系統誤差為-100 m、-0.5×π/180 rad;兩雷達均具有50 m、0.5°的量測隨機誤差。目標在40 km×40 km的矩形區域內做勻速直線運動,目標的運動速度在200 m/s~400 m/s之間。 場景二:雷達B的測距系統誤差、測角系統誤差為200 m、1.5×π/180 rad,雷達B的測距系統誤差、測角系統誤差為-200 m、-1.5×π/180;兩雷達均具有50 m、0.5°的量測隨機誤差。目標在40 km×40 km的矩形區域內做變速直線運動,目標的運動速度在200 m/s~400 m/s之間。 圖9 場景一下兩種算法航跡正確關聯率對比 圖10 場景二下兩種算法航跡正確關聯率對比 通過比較分析圖9和圖10得,在系統誤差較小的情況下,本文算法以及區實混合序列算法都有較高的正確關聯率,在20步時正確關聯率均能達到95%以上。當系統誤差變大時,本文算法性能變化較小,其抗差性能較好;區實算法亦對系統誤差具有一定抗性。 算法性能亦可能受到方位角、距離等因素的影響。目標區域中心以兩部雷達連線的中垂線以北為0°,逆時針旋轉180°,觀察航跡正確關聯率隨角度變化的影響。目標區域中心位于兩部雷達連線中點,此時記距離為0 km,不斷向北移動目標區域,觀察其隨著距離增加航跡正確關聯率的變化。 圖11 場景一下距離對兩種算法正確關聯率的影響對比 通過綜合分析圖11得,距離對區間相離度算法影響較大,而其他兩種算法受距離影響較小;隨著距離的增大,目標真實位置灰區域不斷變大,由此導致錯誤關聯的概率增大;區間相離度算法的正確關聯率下降,在100 km時正確關聯率為90%。 圖12 場景一下方位角對兩種算法正確關聯率的影響對比 通過分析圖12得,方位角對本文算法的性能影響較大,隨著方位角變化,正確關聯率有一定程度的減小,在90°時灰關聯算法的正確關聯率最低,約為80%左右;而區實混合序列相似度算法受方位角影響不大。 分析表1得,在任意周期比情況下,本文算法均能保持很高的正確關聯率;隨著目標運動速度的增大,正確關聯率減小。 表1 不同雷達采樣周期、目標速度大小對算法性能的影響 仿真采用蒙特卡洛方法,下面就每次算法關聯過程耗時進行仿真分析。 圖13 場景一下兩種算法耗時對比 分析圖13得,本文算法與區實混合序列相似度算法相比,算法耗時有一定程度的提高。 本文研究分析了雷達采樣時間差以及雷達系統誤差對航跡量測值的影響,結合對目標機動能力的分析,提出了一種無須時域配準且具有一定抗差能力的異步航跡關聯算法。并將本文算法與文獻[9]中的區實混合序列算法就系統誤差、密集度、距離、方位角、算法耗時等方面進行了仿真比較分析,得到以下結論: 1)在抗系統誤差方面,本文算法與無須時域配準的區實序列相似度算法相比,更為優異,在大系統誤差時,本文算法仍能達到95%。 2)區實混合序列相似度算法需要預知雷達采樣速率比,導致算法適用性較低,而本文算法無須預知速率比,在任何情況下均可適用。 3)本文算法耗時較長,稍高于區實混合序列相似度算法,這也將是下一步研究的重點。


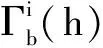

2 航跡異步分析
2.1 目標運動特性分析


2.2 目標位置灰區域描述



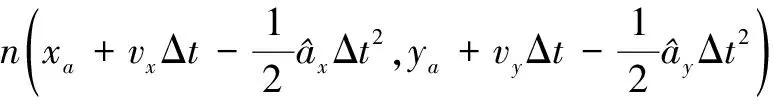
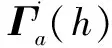
3 系統誤差表示
3.1 航跡點系統誤差表示

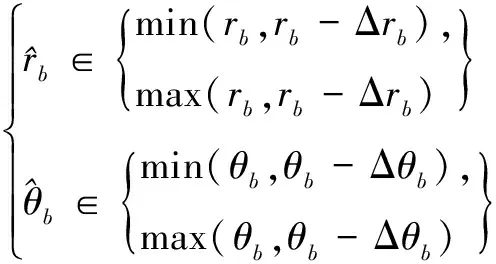
3.2 目標機動區域系統誤差表示
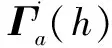


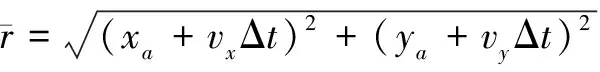



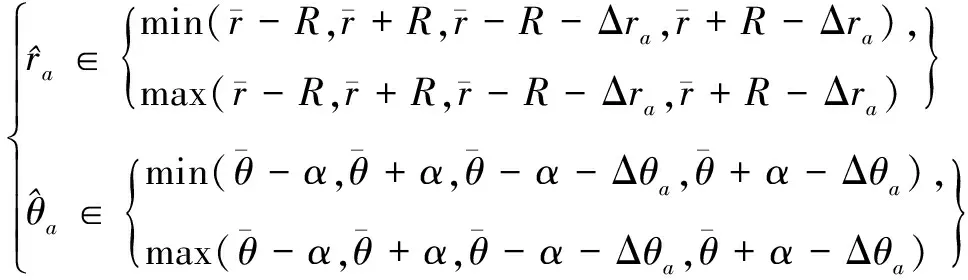

4 算法步驟

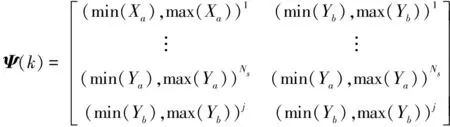




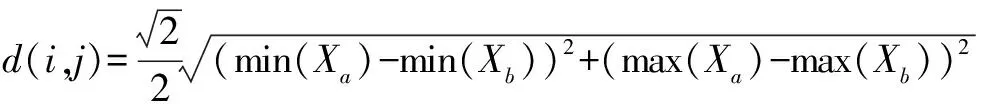
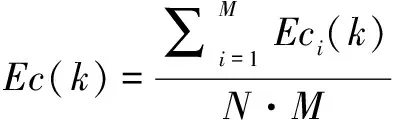
5 仿真分析





6 結束語

