基于先驗信息的彈藥消耗量統計推斷方法*
趙汝東,史憲銘,姜廣勝,2,李正映,李 康
(1.陸軍工程大學石家莊校區裝備指揮與管理系,河北 石家莊 050003;2.陸軍步兵學院石家莊校區,河北 石家莊 050003)
目前彈藥消耗預測主要依賴于對歷史作戰數據的運用,而新型彈藥卻面臨著試驗數據不足的問題,即缺少真實彈藥消耗數據。因此,對新型彈藥進行消耗預計只能借助由歷史數據衍生出的專家經驗值、試驗仿真數據等先驗信息。如何利用現有數據更精確地確定不同毀傷等級下的彈藥消耗量是當前亟須解決的軍事問題,也是彈藥精確保障的關鍵。
現有的彈藥消耗預測方法主要有基于數理模型,如任務量推算法[1]、時間序列分析法[2]、支持向量機[3]等,上述方法都要求有大量的數據支撐,其數據在可信性上需進一步探究;基于作戰模擬,如蘭徹斯特方程[4]、系統動力學[5]、作戰仿真法[6]等,該類方法只能粗糙預測彈藥消耗情況,準確性較低;基于智能算法,如BP神經網絡[7-8]等,同樣需要大量的彈藥消耗數據,對統計數據的可靠性依賴大,上述方法均未考慮新型彈藥消耗數據可信性驗證的問題。如何保證現有彈藥消耗數據在可信范圍之內,以盡可能準確地預計達到各毀傷等級所需彈藥量是當前研究的重點。
為了解決統計數據估計值可信性問題,學者們進行了區間估計,引入置信區間將其限定在一定范圍內。趙洪寶[9]等利用數理統計理論對巖樣單軸抗壓強度置信區間、置信度等問題進行了系統的分析研究,整理并推導出了巖樣單軸抗壓強度“區間估計指標”的理論計算公式;王娟[10]等研究了極大似然估計的漸近正態性法和輪廓似然函數法,求解了Pareto分布中尺度參數的置信區間。徐曉嶺[11]等在全樣本、定數截尾樣本以及缺失數據場合下,分別研究了位置參數、刻度參數的點估計與區間估計問題。
針對新型彈藥歷史消耗數據不足、預測精度較低等問題,本文利用先驗信息對不同毀傷等級下彈藥消耗量總體均值進行極大似然估計,得到確切的彈藥消耗量值;并結合彈藥消耗量分布情況對其均值進行區間估計,確定不同毀傷等級下彈藥消耗量合理的置信區間,進一步縮小范圍擴大精度,檢驗了極大似然估計值的可信性。應用分析驗證了該方法是有效的。
1 基于截尾樣本的最大似然估計
為了滿足彈藥精確保障要求,需預計出不同毀傷等級下彈藥具體消耗情況,故對不同毀傷等級下彈藥消耗量θ進行合理點估計。專家數據、試驗仿真數據等先驗信息經初步處理后,構建不同毀傷等級下的彈藥消耗量置信總體Θ,對其樣本進行極大似然估計[12],取到樣本η1,η2,…,ηn的概率L(θ)最大,此時不同毀傷等級下彈藥消耗量θ的估計值較為合理。
樣本η1,η2,…,ηn的聯合概率密度為
(1)
樣本的似然函數表示為

(2)

(3)
(4)

(5)
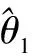
(6)
(7)
2 彈藥消耗量的區間估計指標
2.1 先驗信息下的彈藥消耗分布規律

2.2 確定置信區間
根據數理統計原理,將置信度為1-α時不同毀傷等級下彈藥消耗量總體均值μσi的置信區間[15]定義為
μδi=[δi-low,δi-high]
(8)
其中i代表不同毀傷等級,δi-low為不同毀傷等級下彈藥消耗量總體均值的置信下限,δi-high為不同毀傷等級下彈藥消耗量總體均值的置信下限。

(9)
由t分布的分位數定義知
(10)
即
從而可以確定不同毀傷等級下彈藥消耗量總體均值μσi的一個置信水平為1-α的置信區間為
(11)
其中,不同毀傷等級下彈藥消耗量樣本標準差Si的計算公式為
(12)
3 應用分析
通過咨詢相關領域專家,查閱文獻資料得到了以下數據資料:表1是根據以往彈藥實彈試驗數據獲得的專家經驗值,6個目標裝備達到輕度毀傷L1、中度毀傷L2、重度毀傷L3、報廢L4時的彈藥消耗量,取其均值作為單個目標達到不同毀傷等級下的彈藥消耗量。認為零毀傷即目標未被命中,故不考慮零毀傷的情況。

表1 目標裝備在不同打擊強度下的戰損率對比
在表1專家數據的基礎上,對單個目標達到不同毀傷等級下的彈藥消耗量進行仿真模擬,數據樣本如表2所示,并展開統計推斷研究。

表2 目標裝備達到各級毀傷時的彈藥消耗情況

(13)


表3 目標裝備達到各級毀傷
毀傷等級為零毀傷L0時,目標裝備的作戰效能損失不足5%。根據上述數據借助Origin8.0軟件可以擬合出目標達到不同毀傷等級時的彈藥消耗量曲線,如圖1所示,更直觀看到不同毀傷等級下的彈藥消耗量變化趨勢。

圖1 不同毀傷等級下的彈藥消耗量曲線
4 結束語
本文從數理統計原理出發,借助極大似然估計確定了不同毀傷等級下的彈藥消耗量,并利用彈藥消耗量總體均值的區間估計確定合理的置信區間,檢驗了不同毀傷等級下彈藥消耗量的可信性。通過應用研究對此方法進行了驗證,擬合出了目標達到不同毀傷等級時的彈藥消耗量曲線,可為彈藥保障決策提供指導,具有重要軍事意義。接下來的研究需探索一種能在數據較少條件下進行彈藥需求預計的方法,為新型彈藥消耗預計提供新思路。

