復(fù)合材料曲梁力學(xué)性能研究

朱冬梅 馬濤 劉海平 楊陽

摘 ? 要：設(shè)計一種用于航天發(fā)射臺高剛度組合件中的復(fù)合材料曲梁結(jié)構(gòu)，并對其力學(xué)特性進行試驗及數(shù)值計算研究. 利用微機控制電子試驗機對其進行靜力加載試驗，得到曲梁的載荷-位移特性曲線，并計算得到等效彈性模量. 基于ABAQUS有限元軟件，建立了曲梁的有限元模型，進行不同位移載荷下的數(shù)值模擬計算，利用試驗數(shù)據(jù)對數(shù)值計算結(jié)果進行驗證，計算結(jié)果與實測結(jié)果吻合良好，誤差均在10%以下. 在此基礎(chǔ)上利用有限元模型計算不同載荷下的曲梁縱向和橫向位移，得出曲梁的縱向位移小橫向位移大，橫縱位移比大于10，并研究曲梁厚度、間隙寬度以及中部直梁長度對曲梁力學(xué)性能的影響，得出不同幾何參數(shù)變化對等效彈性模量的影響規(guī)律. 本研究對曲梁應(yīng)用于減隔振裝置提供一定參考.

關(guān)鍵詞： 曲梁;彈性模量;有限元;試驗;載荷-位移特性

中圖分類號：TQ342.94 ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標(biāo)志碼：A

Study on Mechanical Performance of Composite Curved Beam

ZHU Dongmei？覮，MA Tao，LIU Haiping，YANG Yang

（School of Mechanical Engineering，University of Science & Technology Beijing，Beijing 100083，China）

Abstract： In this paper， a composite curved beam structure used in high stiffness components of space launch platform is designed，and its mechanical properties are studied experimentally and numerically. Firstly， the static loading test of the curved beam is carried out by a computer controlled electronic testing machine. The load-displacement characteristic curves of the curved beam are obtained， and the equivalent elastic modulus is calculated. Based on ABAQUS finite element software， the finite element model of curved beam is established， and the numerical computations under different displacement loads are carried out. The experimental data are used to verify the numerical results. The calculated results are in good agreement with the measured results， and the errors are less than 10%. Then， the finite element model is used to calculate the longitudinal and transverse displacements of curved beams under different loads. It is concluded that the longitudinal displacement of curved beam is small， the transverse displacement is large， and the ratio of transverse displacement to longitudinal displacement is greater than 10. The effects of thickness of curved beam， width of clearance， and length of central straight beam on the mechanical properties of curved beam are studied， and the rules of the influence of different geometric parameters on the equivalent elastic modulus are obtained. This study provides a reference for the application of curved beams in the vibration isolation devices.

Key words： curved beam;elastic modulus ;finite element;test;load-displacement characteristics

曲梁是一種結(jié)構(gòu)簡單，具有承載能力、強度和剛度高以及耐疲勞等優(yōu)點，在航空航天、汽車、建筑等領(lǐng)域獲得了廣泛應(yīng)用[1-5]. 目前研究曲梁的方法主要有數(shù)值計算、近似計算和試驗研究. 近年來，國內(nèi)外許多學(xué)者對曲梁的性能做了大量的研究. Ranz等[6]通過試驗研究了具有可變厚度的碳/環(huán)氧樹脂層壓彎曲梁的層間拉伸強度，分析了碳/環(huán)氧樹脂層壓彎曲梁對最大層間拉伸應(yīng)力以及層離演變的影響;馬麗婷等[7]通過四點彎曲試驗和落錘沖擊試驗，研究了復(fù)合材料層合曲梁沖擊前后四點彎曲強度及其破壞模式;Liu等[8]基于譜分解法的線性二次型最優(yōu)控制器的設(shè)計來對作為分布參數(shù)模型的曲梁結(jié)構(gòu)的振動抑制進行了研究;Ghuku等[9]對各種荷載作用下的初始彎曲懸臂梁的大撓度特性進行了理論和試驗研究;黃修長等[10]利用Bloch定理和波向量法分別研究了其阻帶特征和輸入輸出導(dǎo)納特性，分析了周期數(shù)和尺寸參數(shù)對導(dǎo)納的影響，利用傳遞矩陣法研究了曲梁周期結(jié)構(gòu)在基礎(chǔ)為彈性板的單自由度系統(tǒng)中的應(yīng)用;吳曉等[11]用彈性理論研究了拉壓等效彈性模量不同曲梁的平面應(yīng)力及位移的問題，推導(dǎo)出了拉壓等效彈性模量不同曲梁的應(yīng)力及位移表達(dá)式;Poortabib[12]分析了彎曲復(fù)合材料夾層擬層梁在均布荷載作用下的臨界屈曲荷載，研究了各種參數(shù)對梁的臨界屈曲荷載的影響;魯書濃等[13]利用有限元方法對復(fù)合懸臂曲梁進行了數(shù)值分析，求得了復(fù)合懸臂曲梁的正應(yīng)力和切應(yīng)力;Musial等[14]通過測量混凝土和鋼筋混凝土梁的本征頻率的動態(tài)測定方法來確定混凝土的彈性模量;Fraternali等[15]提出了一種復(fù)合曲梁的幾何非線性有限元模型，該模型考慮了截面比較大的旋轉(zhuǎn)、比較大的剪切應(yīng)變、小軸向應(yīng)變以及材料在拉伸和壓縮時的不同彈性響應(yīng);Kumar等[16]提出基于有限元法的組合梁部分分層建模，得到了分層梁在拉伸彎曲、拉伸扭轉(zhuǎn)和扭轉(zhuǎn)彎曲耦合項均質(zhì)截面剛度;郝扣安等[17]研究了彈性地基曲梁的內(nèi)外徑之比對層間正應(yīng)力和平面內(nèi)正應(yīng)力的影響及不同材料對其力學(xué)性能的影響;王元清等[18]利用ANSYS有限元分析曲梁局部參數(shù)（變化翼緣、腹板、加勁肋數(shù)量）對曲梁的承載性能的影響.

本文設(shè)計一種M40碳纖維曲梁結(jié)構(gòu)，其受力時，縱向保持剛度輸出，維持小變形，橫向位移放大，具有良好的減振和抵抗變形的能力. 首先利用試驗得出初始結(jié)構(gòu)參數(shù)下曲梁截面的載荷位移曲線和等效彈性模量，并利用ABAQUS有限元軟件，對曲梁受力過程進行數(shù)值模擬，利用試驗數(shù)據(jù)對有限元模型進行檢驗和修正. 在此基礎(chǔ)上，計算研究曲梁不同幾何參數(shù)對截面等效彈性模量的影響.

1 ? 試 ? 驗

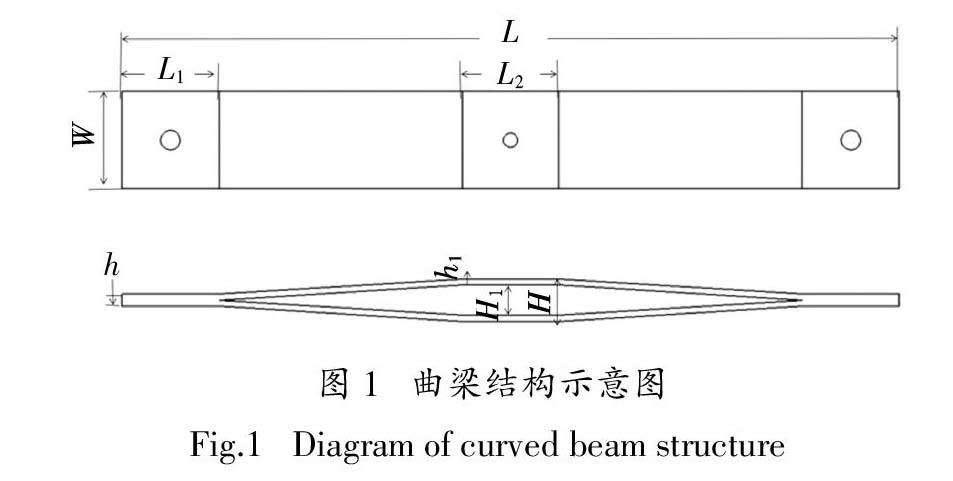
根據(jù)所需曲梁的使用設(shè)計要求和規(guī)格尺寸要求，確定曲梁形狀與尺寸，曲梁的結(jié)構(gòu)示意圖如圖1所示. 曲梁長度L = 400 ?mm，寬度W = 50 mm. 曲梁兩端長度L1 = 50 mm，厚度h = 6.25 mm的直梁，分為上梁下梁兩部分，上梁和下梁厚度均為h1 =3.125 mm;曲梁中部上梁和下梁長度均為L2 = 50 mm的直梁，曲梁中部上下兩梁上端面之間距離為H = 21.8 mm. 上梁與下梁之間留有填充阻尼介質(zhì)的間隙，間隙最大寬度為H1 = 15.55 mm.

■

圖1 ? 曲梁結(jié)構(gòu)示意圖

Fig.1 ? Diagram of curved beam structure

1.1 ? 試驗過程

使用微機控制電子萬能試驗機WDW-100對試驗件進行拉伸試驗，設(shè)備量程為100 kN，精度0.5級，獲得試驗件載荷-位移特性曲線;用AFT1861應(yīng)變調(diào)理器（穩(wěn)定性：0.1%/2 h）和YSV8016動態(tài)信號采集儀（測量精度0.3%）測量記錄應(yīng)變的大小. 應(yīng)變片位置如圖2所示，試驗工裝如圖3所示.

■

圖2 ? 曲梁應(yīng)變片位置

Fig.2 ? Position of the curved beam strain gauge

曲梁的兩端與萬能試驗機相連，試件4點處貼單臂電阻應(yīng)變片，組成4個單臂電橋回路與應(yīng)變儀和動態(tài)信號采集儀相連，采用位移控制，施加靜載荷，實時記錄采集數(shù)據(jù). 試驗加載工況如表1所示，試驗加載過程及數(shù)據(jù)采集系統(tǒng)照片如圖4所示.

■

（a）曲梁 ? ? ? ? ? ? ? ? ? ? ? ? ?（b）試驗工件 ? ? ? ? ? ? ?（c）工裝組合

圖3 ? 試驗工裝

Fig 3 ? Test tooling

表1 ? 曲梁試驗加載工況

Tab.1 ? Load case of the curved beam for test

■

■

（a） 數(shù)據(jù)采集系統(tǒng) ? ? ? ? ? ? ? ? ? （b）曲梁試驗加載

圖4 ? 試驗系統(tǒng)

Fig.4 ? Testing system

1.2 ? 試驗結(jié)果

對試驗數(shù)據(jù)進行處理，得到各工況條件下加載時的載荷-位移特性曲線，如圖5所示.

■

位移/mm

（a）300 N

■

位移/mm

（b）600 N

■

位移/mm

（c）900 N

■

位移/mm

（d）1 200 N

圖5 ? 加載不同載荷下的載荷-位移曲線

Fig.5 ? Load-displacement curves under different loads

從圖5可以看出，試驗件在拉伸時，載荷-位移曲線近似呈線性，加卸載曲線重合性都較好，載荷-位移曲線的線性度和回零情況都較好.

1.3 ? 等效彈性模量

曲梁是對稱結(jié)構(gòu). 對于試件，測點1和測點3以及測點2和測點4其橫截面幾何尺寸相同，如表2所示. 在軸向力（拉伸或壓縮）的作用下，其受力狀態(tài)相同，分別觀察測點3、測點2和測點4的應(yīng)變值，如表3所示，可知應(yīng)變值基本相同. 說明試驗數(shù)據(jù)可靠，可用于曲梁截面I和截面Ⅱ處等效彈性模量的測量.

令εi，j = （εi + εj）/2，其中εi，j表示同一截面不同測點的平均值，i，j表示測點編號.

表2 ? 曲梁截面幾何尺寸

Tab.2 ? Geometry of curved beam section

■

表3 ? 不同力下各測點的應(yīng)變

Tab.3 ? Strain of the measured points

under different forces ? ? ? ? ? ? ? ? με

■

由表3得，Δε1，3的平均值為135.93 με，由公式 E1 = ΔP/Δε1，3 A1得截面I等效拉伸等效彈性模量為7.06 GPa;同理可得Δε2，4的平均值為77.51 με，由公式EⅡ = ΔP/Δε2，4 AⅡ得截面Ⅱ等效拉伸等效彈性模量為24.77 GPa.

2 ? 有限元模型建立及驗證

2.1 ? 模型建立

在ABAQUS中建立曲梁的有限元模型，設(shè)置材料參數(shù)：密度ρ = 1 630 kg/m2;彈性模量E1 = 320 GPa，E2 = 6 200 MPa，E3 = 6 200 MPa;泊松比ν1 =0.30，ν2 = 0.30，ν3 = 0.35;剪切模量G12 = 4 100 MPa，G13 = 4 100 MPa，G23 = 3 500 MPa. 創(chuàng)建50層復(fù)合層，以旋轉(zhuǎn)角為45°/O3 /-45°/O3 /-45°/O3 /45° 的方式鋪層，單層厚度0.125 mm，材料為M40. ?在曲梁上下兩端10 mm處建立參考點RP-1和參考點RP-2，采用八結(jié)點線性六面體單元進行網(wǎng)格劃分，如圖6所示. 采用ABAQUS動力顯示分析方法，設(shè)置接觸和邊界條件，參考點RP-1和參考點RP-2和梁上下兩端側(cè)面剛性耦合，在參考點RP-1處施加y方向拉伸載荷（300 N、600 N、900 N、1 200 N），參考點RP-2處為完全約束.

■

圖6 ? 曲梁有限元模型

Fig.6 ? Finite element model of curved beam

2.2 ? 計算結(jié)果分析

將載荷分別設(shè)置為300 N、600 N、900 N、1 200 N，得到不同載荷下的應(yīng)力云圖，如圖7所示，圖中單位為MPa;載荷-位移曲線如圖8所示.

■

（a）300 N

■

（b）600 N

■

（c） 900 N

■

（d）1 200 N

圖7 ? 不同載荷下的應(yīng)力云圖

Fig.7 ? Stress nephogram under different loads

■

位移/mm

（a）300 N

■

位移/mm

（b） 600 N

■

位移/mm

（c） 900 N

■

位移/mm

（d） 1 200 N

圖8 ? 不同載荷下的載荷-位移試驗與仿真對比曲線

Fig.8 ? Comparison curves of load-displacement

test and simulation under different loads

由圖8可以得出，在載荷分別300 N、600 N、900 N、1 200 N時，對應(yīng)的位移大小分別為0.084 mm、0.14 mm、0.184 mm、0.212 mm，經(jīng)對比計算得出與試驗數(shù)據(jù)誤差分別為5%、6.1%、12.4%、15.2%. 通過圖7應(yīng)力云圖得到對應(yīng)各個測點的應(yīng)變值如表4所示.

表4 ? 曲梁仿真應(yīng)變數(shù)據(jù)

Tab.4 ? Simulation strain data of curved beam

με

■

根據(jù)1.3節(jié)等效彈性模量的計算方法，得到曲梁I截面等效拉伸彈性模量為7.41 GPa，與試驗數(shù)據(jù)誤差為4.9%;Ⅱ截面等效拉伸彈性模量為26.13 GPa，與試驗數(shù)據(jù)誤差為5.5%. 可以看出I、II截面誤差均在10%以下，說明利用ABAQUS數(shù)值分析結(jié)果和試驗實測結(jié)果吻合良好.

2.3 ? 不同載荷下橫縱位移分析

根據(jù)2.1節(jié)設(shè)置的條件，在如圖9所示中梁的a表面和b表面分別建立點集，并歷程輸出位移，分別在300 N、600 N、900 N、1 200 N拉伸載荷作用下，分析歩時間為1 s，隨機選取曲梁上端面a面上節(jié)點的最大位移取平均值，a面上節(jié)點的位移即為縱向位移.同理隨機選取曲梁外側(cè)面端面b面上節(jié)點的最大位移，求出平均值. 由于曲梁是對稱結(jié)構(gòu)，從仿真結(jié)果得出b面關(guān)于YOZ對稱面c面和b面位移相同，故b面上的節(jié)點在橫向上的兩倍位移即為梁的橫向位移. 計算出的結(jié)果如表5所示.

■

圖9 ? 橫縱面的示意圖

Fig.9 ? Schematic diagram of horizontal and vertical planes

表5 ? 不同載荷條件下曲梁橫縱向位移

Tab.5 ? Longitudinal and transverse displacement

of curved beam ?under different loads

■

從表5可以得出，曲梁在受拉伸載荷條件下，縱向維持小變形，而橫向位移較大，橫縱位移比大于10，體現(xiàn)了縱向保持剛度輸出、維持小變形、橫向位移放大的特點.

3 ? 曲梁各參數(shù)對曲梁性能的影響

3.1 ? 曲梁厚度

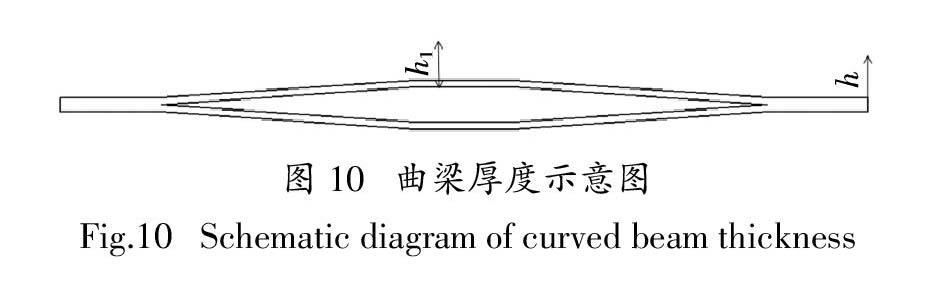
曲梁的厚度h是曲梁重要的參數(shù)之一，也是對曲梁性能尤其是彈性模量有著重要影響的因素之一. 根據(jù)曲梁的設(shè)計要求，曲梁中部寬度為設(shè)計基準(zhǔn)，改變厚度時梁的寬度不應(yīng)發(fā)生變化，仍保持H = 21.8 mm. 為得到較為精確的數(shù)據(jù)，曲梁厚度變化位置如圖10所示.

■

圖10 ? 曲梁厚度示意圖

Fig.10 ? Schematic diagram of curved beam thickness

設(shè)置曲梁的厚度h1分別為5.75 mm、6 mm、6.25 mm、6.5 mm、6.75 mm，分別對不同厚度的曲梁加載，載荷分別為300 ?N、600 N、900 N、1 200 N，利用有限元仿真得到位移變化值，如表6所示. 根據(jù)1.3節(jié)等效彈性模量的計算方法得到等效彈性模量如圖11所示.

表6 ? 不同曲梁厚度下的位移

Tab.6 ? Displacement of curved beams with

different thicknesses ? ? ? ? ? ? ? ? ? ? ? ?mm

■

■

厚度/mm

圖11 ? 不同厚度截面等效彈性模量

Fig.11 ? Elastic modulus curves of different thickness sections

從表6可以得出，當(dāng)曲梁厚度發(fā)生變化時，曲梁在載荷較小時位移差別較為明顯，但隨著載荷的增加，位移差逐漸減小，可以認(rèn)為曲梁厚度對曲梁的拉伸位移影響較小. 從圖11可以看出，Ⅰ截面、Ⅱ截面和等效彈性模量變化趨勢一致，等效彈性模量均隨著厚度的減小而增大，呈現(xiàn)于曲梁厚度相反的變化趨勢. 產(chǎn)生上述變化的原因可能是曲梁厚度的增加，而梁的受載不變，增厚的橫截面面積遠(yuǎn)大于應(yīng)變減小后的應(yīng)變量，由公式Ex = ΔP/Δεi，j Ax可知，彈性模量隨著厚度的增大而減小;從仿真結(jié)果可以看出，隨著厚度的增大，Ⅰ截面和Ⅱ截面的應(yīng)力和名義應(yīng)變都減小，但截面的應(yīng)力值與名義應(yīng)變值之比是減小的，故兩截面的等效彈性模量不斷減小.

3.2 ? 曲梁間隙寬度H1對曲梁性能的影響

本曲梁作為發(fā)射平臺隔振的關(guān)鍵零件，以阻尼填充的間隙寬度為設(shè)計基準(zhǔn)，故曲梁間隙寬度也是重要的參數(shù). 改變曲梁間隙對曲梁的性能影響進行仿真數(shù)據(jù)分析，根據(jù)曲梁的設(shè)計要求，曲梁厚度保持不變，仍保持h = 6.25 mm. 為得到較為精確的數(shù)據(jù)，曲梁間隙寬度變化位置如圖12所示.

■

圖12 ? 曲梁間隙寬度變化位置示意圖

Fig.12 ? Sketch of curved beam gap width

設(shè)置曲梁的間隙寬度H1分別為13.75 mm、14.75 mm、15.75 mm，16.75 mm、17.75 mm，分別對不同間隙寬度的曲梁加載，加載載荷分別為300 N、600 N、900 N、1 200 N，利用有限元仿真得到位移變化值，如表7所示;根據(jù)1.3節(jié)等效彈性模量的計算方法得到等效彈性模量如圖13所示.

表7 ? 不同曲梁間隙寬度下的位移

Tab.7 ? Displacement of curved beams with

different clearance widths ? ? ? ? ? ? ? ? ? mm

■

■

寬度/mm

圖13 ? 不同間隙寬度下截面等效彈性模量

Fig.13 ? Elastic modulus curves of different clearance widths

根據(jù)表7可以得出，當(dāng)曲梁的間隙寬度發(fā)生變化時，曲梁拉伸位移隨載荷的增減而變化較為明顯，隨間隙寬度的增加，曲梁的拉伸位移增大. 由圖13得出Ⅰ截面、Ⅱ截面的等效彈性模量呈相反的變化趨勢，Ⅰ截面等效彈性模量隨曲梁間隙增大而減小，Ⅱ截面等效彈性模量隨曲梁間隙增大而增大. 從仿真結(jié)果可以得出，當(dāng)間隙增大時，I截面名義應(yīng)變值變大而橫截面面積不變，由Ex = ΔP/Δεi，j Ax得出等效彈性模量減小;截面Ⅱ由于間隙增大，名義應(yīng)變值減小，則等效彈性模量增大.

3.3 ? 中部直梁長度L2對曲梁性能的影響

曲梁上梁和下梁的夾角α也是影響阻尼間隙面積大小的因素，在不改變曲梁間隙寬度H1的條件下，可以通過改變中部直梁的長度L2來實現(xiàn)，如圖12所示. 根據(jù)曲梁的設(shè)計要求，曲梁厚度保持不變，仍保持h = 6.25 mm，曲梁中部上下兩梁上端面之間距離保持不變，保持H = 21.8 mm. 曲梁中部直梁長度變化位置如圖14所示.

■

圖14 ? 中部直梁示意圖

Fig.14 ? Schematic diagram of central straight beam

設(shè)置曲梁的中部直梁長度L2分別為30 mm、40 mm、50 mm、60 mm、70 mm，分別對不同中部直梁長度的曲梁加載，加載載荷分別為300 N、600 N、900 N、1 200 N，利用有限元仿真得到位移變化值如表8所示;根據(jù)1.3節(jié)等效彈性模量的計算方法得到等效彈性模量如圖15所示.

表8 ? 不同曲梁中部直梁長度下的位移

Tab.8 ? Displacement of curved beams different length

of the middle straight beam ? ? ? ? ? ? ? ? ? ? ?mm

■

■

長度/mm

圖15 ? 中部直梁長度不同時截面等效彈性模量

Fig.15 ? Elastic modulus under different lengths

of the middle straight beam

由表8和圖15可以得出，當(dāng)曲梁的中部直梁長度發(fā)生變化時，曲梁拉伸位移隨載荷的增減而存在較為微小的變化. 隨直梁長度的增加，曲梁的拉伸位移增大;由于其他條件不變，中部直梁長度的增加，Ⅰ截面、Ⅱ截面的名義應(yīng)變都有變大的趨勢，兩截面的橫截面積不變，由Ex = ΔP/Δεi，j Ax得出Ⅱ截面的等效彈性模量減少顯著，Ⅰ截面等效彈性模量雖然減小但變化不大，這是由于截面的名義應(yīng)變值增加不大的緣故.

4 ? 結(jié) ? 論

本文對一種隔振曲梁進行力學(xué)性能研究，研究其主要截面的等效彈性模量和不同載荷下拉伸位移的變化趨勢. 采用試驗研究與有限元數(shù)值模擬相結(jié)合的方法，通過多組數(shù)據(jù)的對比分析得到變化規(guī)律. 本文研究的主要結(jié)論如下：

1）使用微機控制電子萬能試驗機WDW-100對試驗件進行拉伸試驗，梁在拉伸載荷下縱向出現(xiàn)微變形，在載荷分別為300 N、600 N、900 N、1 200 N時，對應(yīng)的位移大小分別為0.084 mm、0.14 mm、0.184 mm、0.212 mm，經(jīng)對比計算得出與試驗數(shù)據(jù)誤差分別為5%、6.1%、12.4%、15.2%. 曲梁的Ⅰ截面等效拉伸彈性模量為7.41 GPa，與試驗數(shù)據(jù)誤差為4.9%;Ⅱ截面等效拉伸彈性模量為26.13 GPa，與試驗數(shù)據(jù)誤差為5.5%.Ⅰ、Ⅱ截面誤差均在10%以下，說明利用ABAQUS數(shù)值分析結(jié)果和試驗實測結(jié)果吻合良好，驗證了有限元仿真的有效性.

2）通過ABAQUS對曲梁的縱向和橫向的位移仿真，得出曲梁的縱向位移較小，橫向位移放大，橫縱位移比大于10，很好地體現(xiàn)了梁在縱向剛度輸出橫向位移放大的特點.

3）通過對曲梁厚度的仿真結(jié)果分析，可以計算出梁的重要截面的等效彈性模量，隨著曲梁厚度的增加，曲梁拉伸位移逐漸減小. 重要截面的等效彈性模量變化趨勢一致，等效彈性模量均隨著厚度的減小而增大，呈現(xiàn)于曲梁厚度相反的變化趨勢.

4）通過對曲梁間隙寬度的仿真結(jié)果分析可以發(fā)現(xiàn)，當(dāng)曲梁的間隙寬度發(fā)生變化時，曲梁拉伸位移隨載荷的增減其變化較為明顯，隨間隙寬度的增加，曲梁的拉伸位移增大. 重要截面的等效彈性模量呈相反的變化趨勢，Ⅰ截面等效彈性模量隨曲梁間隙增大而減小，Ⅱ截面等效彈性模量隨曲梁間隙增大而增大.

5）通過對曲梁中部直梁長度的兩組數(shù)據(jù)分析可以發(fā)現(xiàn)，當(dāng)曲梁的中部直梁寬度發(fā)生變化時，曲梁拉伸位移隨載荷的增減而存在較為微小的變化，隨直梁長度的增加，曲梁的拉伸位移增大. 重要截面的等效彈性模量具有相同變化趨勢，等效彈性模量均隨直梁長度增大而減小.

參考文獻

[1] ? KURKIN E I，SADYKOVA V O. Application of short fiber reinforced composite materials multilevel model for design of ultra-light aerospace structures[J]. Procedia Engineering，2017，185：182—189.

[2] ? ?TAN E L，UY B. Experimental study on curved composite beams subjected to combined flexure and torsion[J]. Journal of Constructional Steel Research，2009，65（8）：1855—1863.

[3] ? ?關(guān)天發(fā)，袁鴻. CFRP加固鋼筋混凝土曲梁的抗彎性能試驗研究[J].中山大學(xué)學(xué)報（自然科學(xué)版），2008，47（S2）：109—113.

GUAN T F，YUAN H. Experimental study on bending properties of RC curved beams strengthened with CFRP[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni，2008，47（S2）：109—113. （In Chinese）

[4] ? ?李威，郭權(quán)鋒. 碳纖維復(fù)合材料在航天領(lǐng)域的應(yīng)用[J]. 中國光學(xué)，2011，4（3）：201—212.

LI W，GUO Q F. Application of carbon fiber composites in cosmonautic fields[J]. Chinese Optics，2011，4（3）：201—212.（In Chinese）

[5] ? ?俞璦權(quán)，盧朕. 碳纖維復(fù)合材料在汽車行業(yè)的應(yīng)用[J]. 上海汽車，2013（7）：48—52.

YU A Q，LU Z. Application of carbon fiber composites in automobile industry[J]. Shanghai Automobile，2013（7）：48—52.（In Chinese）

[6] ?RANZ D，CUARTERO J，MIRAVETE A，et al. Experimental research into interlaminar tensile strength of carbon/epoxy laminated curved beams[J]. Composite Structures，2017，164：189—197.

[7] ? ?馬麗婷，陳新文，王翔，等. 碳纖維復(fù)合材料曲梁沖擊后四點彎曲強度及損傷失效模式研究[J]. 玻璃鋼/復(fù)合材料，2017 （3）：17—20.

MA L T，CHEN X W，WANG X，et al. Study on the post impact beam strength and failure mode of carbon/epoxy laminates [J]. Grp/Composite，2017 （3）： 17—20. （In Chinese）

[8] ? ?LIU F S，JIN D P，WEN H. Optimal vibration control of curved beams using distributed parameter models[J]. Journal of Sound and Vibration，2016，384：15—27.

[9] ? ?GHUKU S，SAHA K N. A theoretical and experimental study on geometric nonlinearity of initially curved cantilever beams[J]. Engineering Science and Technology an International Journal，2016，19（1）：135—146.

[10] ?黃修長，徐時吟，華宏星，等. 曲梁周期結(jié)構(gòu)動力學(xué)特性和隔振性能[J]. 上海交通大學(xué)學(xué)報，2013，47（2）：173—179.

HUANG X C，XU S Y，HUA H X，et al. Research on dynamic properties and vibration isolation performance of curved beam periodic structure. [J] Journal of Shanghai Jiao Tong University，2013，47（2）：173—179.（In Chinese）

[11] ?吳曉，楊立軍. 拉壓等效彈性模量不同曲梁的彈性理論解[J]. 工程力學(xué)，2013，30（1）：76—80.

WU X，YANG L J. The elastic theory solution for curved beam with difference elastic modulus in tension and compression[J]. Engineering Mechanics，2013，30（1）：76—80. （In Chinese）

[12] ?POORTABIB A. Critical buckling load of curved sandwich beams with composite skins subjected to uniform pressure load[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering，2016，38（6）： 1805—1816.

[13] ?魯書濃，虞愛民，朱金龍，等. 復(fù)合懸臂曲梁力學(xué)性能的研究[J]. 實驗室研究與探索，2008，27（5）：26—30.

LU S N，YU A M，ZHU J L，et al. Research on mechanical performance of composite cantilever beams[J]. Research and Exploration in Laboratory，2008，27（5）：26—30. （In Chinese）

[14] MUSIAL M，GROSEL J. Determining the young's modulus of concrete by measuring the eigenfrequencies of concrete and reinforced concrete beams[J]. Construction and Building Materials，2016，121：44—52.

[15] ?FRATERNALI F，SPADEA S，ASCIONE L. Buckling behavior of curved composite beams with different elastic response in tension and compression[J]. Composite Structures，2013，100：280—289.

[16] KUMAR S K， GANGULI R， HARURSAMPATH D. Partial delamination modeling in composite beams using a finite element method[J]. Finite Elements in Analysis and Design，2013，76： 1—12.

[17] ?郝扣安，王振清，周利民，等. 彈性地基復(fù)合曲梁抗彎力學(xué)性能研究[J]. 哈爾濱工程大學(xué)學(xué)報，2014，35（5）：552—557.

HAO K A ，WANG Z Q ，ZHOU L M，et al. Flexural behavior of composite curved beams on an elastic foundation [J]. Journal of Harbin Engineering University， 2014， 35（5）： 552—557.（In Chinese）

[18] ?王元清，劉莉媛，丁大益，等. 合肥新橋國際機場柱計算長度及曲梁參數(shù)分析[J]. 沈陽建筑大學(xué)學(xué)報（自然科學(xué)版），2011，27（3）：474—479.

WANG Y Q，LIU L Y，DING D Y，et al. Colum effective length factor and girder parametric analysis for the components of Xing Qiao international airport terminal[J]. Journal of Shenyang Jianzhu University（Natural Science）， 2011， 27（3）： 474—479. （In Chinese）