基于偏置比例導引的垂直攻擊滑模制導律
穆忠偉,吳 劍,韓秀楓
(南昌航空大學信息工程學院,南昌 330063)
0 引言
導彈自第二次世界大戰問世以來,受到各國普遍重視,得到很快發展。導彈的使用,增大了戰爭的突然性和破壞性,擴大了戰爭的規模和范圍,且加快了戰爭進程,從而改變了過去常規戰爭的時空觀念,給現代戰爭的戰略戰術帶來巨大而深遠的影響[1]。隨著精確制導武器的不斷改進,除了命中精度這項基本要求外,還需要在命中時刻具有垂直攻擊角度,以提高戰斗部的毀傷效能。
自從Kim和Grider首次在機動彈頭再入制導的研究中引入落角約束問題以來,一些學者根據不同的應用背景及不同的理論方法提出了多種具有終端角度約束的制導律,主要包括最優制導律、滑模變結構制導律、改進的比例制導律以及其他類型的制導律[2-4],并取得了豐富的成果。文獻[5]設計了帶終端角度約束的變結構制導律,在目標不機動和隨機機動的情況下都能滿足攻擊角度的要求,同時給出了制導律的收斂性證明;文獻[6]介紹了一種新導引律的設計方法,改善了彈道特性和制導系統的魯棒性,但仍無法提供對終端狀態的保證;文獻[7]針對導彈以一定角度攻擊特定目標的問題,提出了基于多項式函數的落角約束制導律方法;文獻[8]針對導彈要求限制末端攻擊角度的作戰要求,基于滑模變結構控制理論,面向機動目標,設計了一種滿足脫靶量及攻擊角度約束的制導律;文獻[9]對彈目相對運動作線性近似后,基于二次型最優控制理論給出了俯沖擊頂制導律,但其缺點是需要估計剩余時間,以及求解比較復雜的微分方程兩邊的邊值問題;文獻[10]針對遠距離攔截高速、大機動目標的攔截弧度長的問題,在滿足攻擊角度的約束條件下,通過引入分段線性和指數兩種形式的阻尼,使得導彈在攔截高速高加速目標時,對目標機動的敏感度隨彈目距離變化,從而達到能量管理的目的;文獻[11]針對臨近空間高超聲速巡航飛行器攔截所面臨的制導策略,提出了采用高拋彈道攔截的設計方法。
本文針對空地導彈攻擊地面固定目標的問題,在傳統的比例導引律的基礎上,增加了一個角度偏置項,并結合滑模變結構的控制理論,設計了一種新型垂直攻擊目標的制導律。該制導律克服了終端角度無法約束的問題,并詳細地對比了其與傳統比例制導律在攻擊地面目標時的不同,驗證了本文中所設計制導律的優越性能。
1 彈目相對運動建模與分析
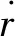
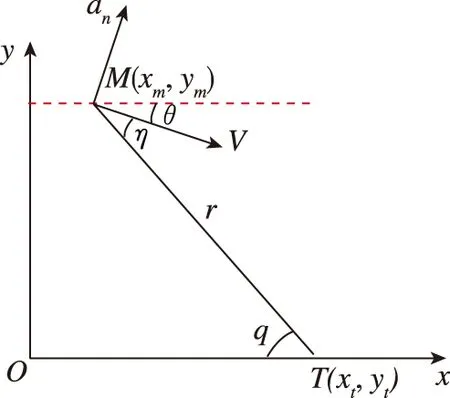
圖1 導彈-目標相對運動關系Fig.1 Missile-target relativemotion relation
根據導彈與目標的相對關系得出了相對運動方程為
(1)
2 導引律設計
2.1 導引律推導
由于末制導段多采用響應速度較快的過載駕駛儀,常以法向加速度指令作為指令信號,因此假定導彈采用具有如下結構的偏置比例導引的制導律形式為
(2)
式中,K≥2,u為偏置項。
對式(1)第二項求導可得
(3)
進而可得
(4)
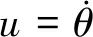
(5)
2.2 自適應垂直攻擊結構項的設計
要保證導彈最終以期望角度攻擊目標,并以零化視線角速度完成攻擊任務,令
x1=q(t)-qf
(6)
(7)
式(6)中,qf為落點處的期望視線角度。若使狀態x1趨于0,則可實現以期望的攻擊角度接近目標的任務;若使狀態x2趨于0,則能夠以保持固定的角度攻擊目標,提高了擊中目標的性能。
式(6)、式(7)的終端約束條件為
首先需要選擇設計一個滑模切換平面,以迫使系統在一定特性下沿規定的狀態軌跡做小幅度、高頻率的上下運動,即滑模運動。為了在制導過程中使狀態x1和x2逐漸趨于0,同時滿足零化脫靶量和末端落角的要求,故設計切換函數[14]為
S=x2+λVx1/r
(8)
其中,λ為大于0的常數。當S=0時,系統處于滑模運動狀態,此時x1=x2=0,導彈可以按照期望落角命中目標。
當系統在有限時間內到達切換平面后進入滑動模態,系統要滿足可達性條件
(9)
可達性條件保證了系統運動在有限時間內到達切換平面,但對這段時間內具體的狀態軌跡沒有約束。為了改善這段運動的動態品質,通過設計趨近律來加以控制。選取具有自適應特性的指數趨近律
(10)
式中:w>0,ε>0。
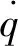
現將式(8)求導可得
進而
(11)
將式(10)與式(11)聯合求得
進而可得
(12)
將式(12)代入式(5)中可得
u=
進而可得
u=
(13)
將式(13)代入可得
(14)
2.3 穩定性分析
應用Lyapunov方法對系統穩定性進行分析。選擇Lyapunov函數為
(15)
則有
(16)
即得系統在Lyapunov意義下是漸近穩定的。
2.4 基于連續切換的滑模控制變結構制導律
在滑動模態控制系統中,如果控制結構的切換具有理想的開關特性,則能在切換面上形成理想的滑動模態,這是一種光滑的運動,漸近收斂于原點。但在實際工程應用中,由于存在時間上的延遲和空間上的滯后等原因,使得滑動模態呈現抖振形式,即在光滑的滑動模態上疊加有抖振。抖振問題是影響滑動模態控制的主要問題。
為了削弱抖振,需要引入繼電特性連續化的方法代替符號函數sgn(s),實現準滑模動態控制,即在邊界層外采用正常的滑模控制,在邊界層內采用連續狀態反饋控制[16-18],旨在避免或削弱抖振影響
(17)
其中,δ是很小的正常數。將式(17)代入導引律式(14)中得
(18)
可見式(18)基于偏置比例導引的滑模制導律主要由兩項組成,第一項為與視線角速度成正比的比例導引項;第二項為根據落角約束確定的滑模變的偏置項。
3 仿真分析
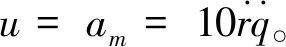
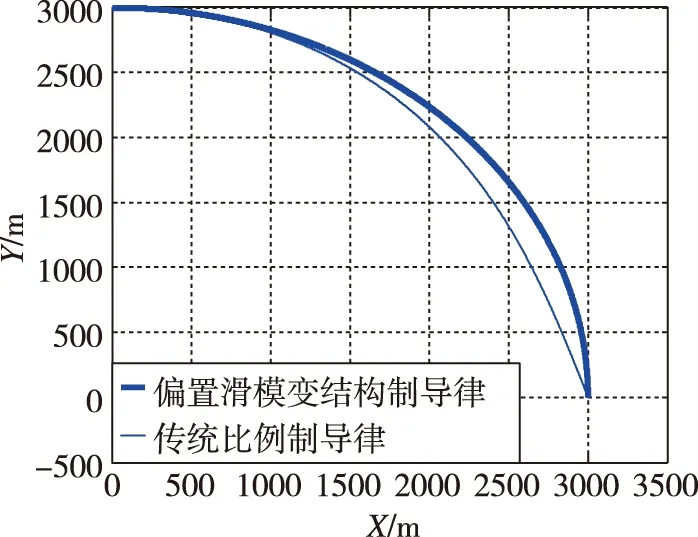
圖2 兩種制導律的彈道軌跡曲線Fig. 2 Trajectories of two guidance laws
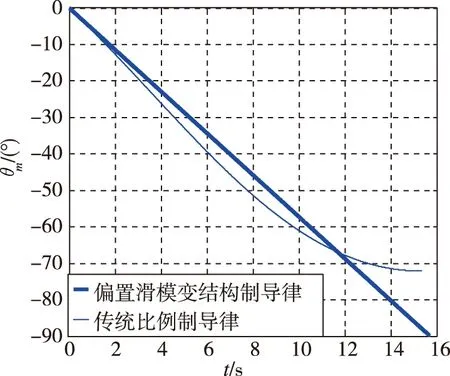
圖3 兩種制導律的彈道傾角曲線Fig.3 Trajectory inclination angle curves of two guidance laws
圖4 兩種制導律的加速度曲線Fig.4 Acceleration curves of two guidance laws
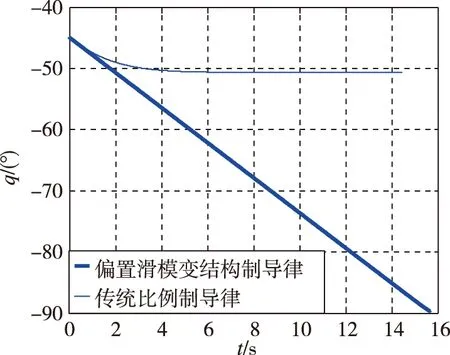
圖5 兩種制導律的視線角曲線Fig.5 Line of sight of two guidance laws
由表1可以看出,偏置滑模結構制導時間是15.7100,大于比例導引的制導時間15.3300,故帶偏置比例導引滑模制導律的制導時間比傳統比例導引律的制導時間稍長。這是由于傳統比例導引的彈道曲線較低,而偏置滑模結構導引的彈道曲線較高(如圖2所示)的緣故。但是這對導彈進行低空突防是非常有利的,尤其是在實際情況中,較高的彈道可以為導彈提供更快的攻擊速度,增大毀傷效果。從仿真結果可知,變結構制導律脫靶量更小,具有更高的制導律精度。
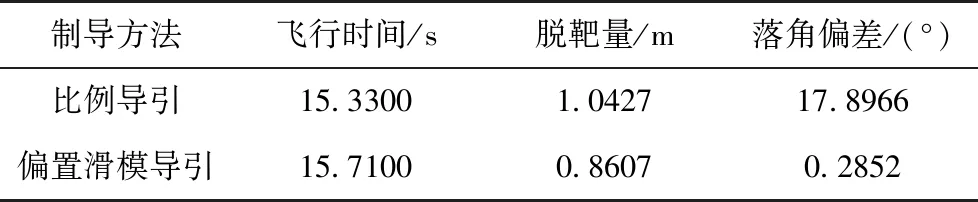
表1 兩種導引律制導效果的比較
由圖4可以看出,在導彈制導過程中,兩種方法的加速度都在增大,但偏置變結構制導律的最大過載比傳統比例導引律的最大過載要小得多。隨后二者過載都開始減小,偏置變結構制導律的過載最后趨向于0,然而傳統比例制導律的過載變小,后又再次增大,所以前者的過載趨于零變化,降低了對導彈執行機構的要求,更易于應用在實戰中。
結合表1與圖3可知,偏置比例的滑模制導律的落角偏差是0.2852,而傳統比例導引的落角偏差是17.8966。從中可以看出,偏置比例滑模的方法要比傳統導引攻擊的角度更加接近90°,幾乎以垂直的方式攻擊地面目標,提高了攻擊目標的毀傷效果;而傳統比例導引偏差過大,無法以90°角攻擊目標。
4 結束語
本文通過建立縱向平面內彈目相對運動學模型,在傳統比例導引律的基礎上,利用落角和脫靶量的約束條件,結合滑模變結構理論設計了一個落角約束偏置項,推導得到了滿足垂直攻擊落角的導彈制導律,并與傳統比例導引律進行了對比仿真。通過選取合理的制導律參數,可以使導彈的法向過載在攻擊目標的過程中逐漸趨向于0,這是傳統比例制導律所不能達到的,并通過仿真驗證了該制導律的有效性和優越性。

