基于龕深及其上覆土層穩定性的崩壁崩坍形成條件研究

馬鵬飛，許文年，夏 棟，夏 露，嚴雨潔1，，鄧羽松

（1.三峽大學 生物與制藥學院，湖北 宜昌443002；2.三峽大學 三峽庫區地質災害教育部重點實驗室，湖北 宜昌443002；3.三峽大學 三峽地區地質災害與生態環境湖北省協同創新中心，湖北 宜昌443002；4.華中農業大學 資源與環境學院，湖北 武漢430070）

崩崗作為中國南方低緩丘陵山區特有的一種自然災害，用來描述一種紅壤區山坡土壤或花崗巖巖石風化殼地表在地貌地形（如坡向、坡形、高程）、地層組合、水力特性、干濕效應、重力、人類活動等影響因子耦合疊加下，不斷地被剝離、崩坍（塌）、陷蝕、堆積后形成深切圍椅狀崩口崖壁地理實體的廣泛存在的土侵蝕現象［1-4］，其子系統包括集水坡面、崩壁、崩積堆、沖刷溝道及沖積扇［5］。崩崗是水土流失中極端的一種侵蝕狀態，是溝谷侵蝕和生態系統退化的高級階段，亦是土壤侵蝕的最高表現形式，有學者形象地視崩崗景觀為“爛山”、“潰瘍”、“劣地”［6-8］。崩壁是風化殼土體在重力與水力的作用下發生滑塌、傾倒等變化而產生的極不穩定的陡壁［9］（坡度多＞60°），是集水區與崩溝系統的交界面，是崩崗再次發生后續侵害的基礎［5，10-11］。崩壁在坡面某處因地表徑流侵蝕而內凹，其凹陷的區域就稱為龕，龕的孕育與形成是崩崗形成的初級階段［12-13］，當龕出現并擴大后，其上覆紅黏土層失去支撐，使崩壁處于欠穩定狀態，才為崩壁崩塌及后退創造條件。

長期以來，國內學者一直致力于崩崗成因及其侵蝕規律的研究，并主要從地質地貌、坡向、植被覆蓋、土壤理化特性（機械組成、分形特征、微結構、土水特征參量等）、抗蝕性、花崗巖不同層次巖土特性（包括抗剪強度、可塑性能、崩解特性、脹縮特質）與崩崗發育之間的聯系等方面展開［8，14-16］，且取得了較好的成就。可是在某些方面，諸如，有關崩壁幾何因素與崩崗成因之間的關系及崩壁防治方法多為定性描述，定量模型的建立較為欠缺［9，17-18］；其次，數值方法具有可重復性、直觀性、數據容易提取等優點［19］，但涉及崩崗侵蝕領域的研究多集中于監測或試驗手段［20］，缺乏嚴謹的數學力學理論基礎，在數值研究方面鮮有探討，難以清晰地揭示崩壁失穩滑移面的漸進擴展過程；再者，土層抗剪強度是土壤含水量的函數，可直接表達崩壁土體的穩定程度，故崩壁的穩定性系數可表示為土抗剪強度的泛函，然而將抗剪強度引入對崩崗穩定性的研究嚴重稀少［5］，以至于無法定量地分析水分與崩壁崩坍之間的聯系；最后，目前崩崗研究側重于事后治理工作，但傳統崩崗綜合防治措施沒有嚴謹的理論支撐，不僅治理工程周期長、成效低，有時反而會在一定程度上促使崩崗的發展，這恰恰增加了對預測預報崩崗土壤侵蝕及崩壁崩坍幾率的需求［5，21-22］。野外調查證實［10］，龕形態的變化（主要表現為其凹陷深度的增加）能有效反映崩崗發展強度的大小，對揭示崩壁溯源侵蝕規律有直接意義。然而在過去［23-24］對崩壁龕的研究多停留在對龕下定義、龕發育歷程及其形成原因的描述等層面，對龕形態的演化進行多年測量統計的工作［10］少有報道。龕的發育程度與崩壁失穩崩塌之間的定性關系較明確，但對二者之間定量關系研究仍處空白，二者定量研究可作為崩崗成因機理研究、崩崗防治的理論基礎，可用來預測預報崩壁崩落時機。為此，有必要建立崩壁—龕分析模型，在前人的既有成果基礎上開展進一步地深入研究。

在天然狀態下，當且僅當龕的發育規模（或龕深）足夠大，崩壁才會發生明顯的崩塌后退破壞［10］；退一步講，如龕深較小時，若崩崗壁各層次土壤含水量足夠大是否也會觸發明顯崩坍呢？基于此，本文以湖北省咸寧市通城縣內的一處崩壁剖面為范例，依托Abaqus軟件平臺，建立崩壁連同龕的有限元分析概念模型。采用對砂土層由外向內分級開挖的方式來模擬龕深的時空演變，計算觸發該范例崩壁明顯崩塌所需的龕臨界深度值。通過設計9組正交有限元試驗方案，改變算例的原始參數，對影響崩壁崩坍難易度的崩壁坡度、崩壁高度、龕高所占砂土層厚度的比例、水分含量進行了因素主次評價；針對正交試驗得出的最優解（使崩壁處于最穩定狀態的解析解），進一步尋找若干較小的龕深與引起崩壁崩坍所需的龕上覆土層最小含水量之間的定量關系，以期為崩崗失穩的預測提供數理依據。

1 研究區概況及數據處理

1.1 研究區概況

鄂東南通城縣崩崗侵蝕區是湖北省崩崗集中分布的典型地區，其崩崗的發生規律在南方具有很好地示范性，因此選擇該縣境內五里社區為供試土樣采集地。阜山北麓通城地區屬北亞熱帶季風氣候區，溫暖濕潤，年內降雨量時空分配不均，光照適中，四季分明，雨熱同期，東南西三面環山，北面平坦，地勢南高北低，海拔高程142 m，全縣土地面積共計1 172 km2［25］，土壤類型為紅壤。多年平均氣溫約16.3℃，日最高氣溫39.7 ℃，極端最低氣溫－15.2 ℃，＞10 ℃的積溫為5 058℃，多年平均降水量1 550 mm，年平均徑流深795 mm，無霜期260 d。據遙感顯示，全縣有大小崩崗1 102個，年土壤流失量達1.20×106t，占通城侵蝕總量的58.4%。在該地崩崗發生造成工民建筑、良田、湖庫溝渠、交通路線等遭到嚴重損毀，導致較大經濟損失。

本研究選取的崩壁仍處于發展狀態，其剖面結構自上而下被劃分為：表土層A（有機質和游離Fe2O3含量高，土粒細膩，偶有大顆粒石英，長石、云母已完全風化，厚0.5 m）、紅土層B（土質均勻，土粒細膩緊實，長石、云母已完全風化，黏粒含量高，厚4.5 m）、砂土層C（高嶺石含量高，有機質和游離Fe2O3含量低，脹縮性弱，原狀土結構較松散，粒徑較紅黏土明顯增大，由石英、半風化或未風化徹底的長石和云母構成，厚2.5 m）和未出露碎屑層D（保持花崗巖原生構造）。受燕山運動劇烈的南北向擠壓力及地應力場等影響，鄂東南花崗巖土體內發育了多組節理和裂隙。尤其是垂直節理的強烈發育，利于崩壁崩坍發生［26］，主要節理產狀為320°∠77°，48°∠75°［12］。采樣點處崩壁坡面平均傾角經勘察為70°。

差異性風化改造使崩壁形成獨特的巖土分層結構，具有一定的土壤退化特性，不同層位性質（如礦物成分、孔隙度、力學強度、物質遷移、導水率）空間分異懸殊，使得各土層抗水流、抗侵、抗崩解、抗崩坍等能力差異較大。砂土層C 是崩壁崩塌的關鍵層次，它強度較低，崩解速率高且抗沖蝕能力極低，受水力影響較大，遇水弱化性極強。地表徑流從集水坡面流下，在上層土體形成造崖層的小型瀑布，進而轉化為瀑流，下部砂土體被不斷淘蝕并剝落后極易形成濺蝕坑，進而擴大成侵蝕龕［4，23］（見圖1）。

圖1 研究區崩壁侵蝕龕現場實景圖片

崩壁坡體由龕上覆紅黏土邊坡SP1（由土層A 和土層B 構成）和砂質土邊坡SP2（由土層C 和土層D構成）組合為復合邊坡［27］。SP1土體抗沖蝕性較強，持水能力大易吸濕增重，當含水率較低時堅硬易開裂，強降雨期飽和度大時減壓膨脹呈塑性［28］。SP2遇水易解體掉塊，土壤結構穩定性小，其水穩性指數IPSP2?IPSP1。因龕的存在，SP1易與下覆土層配合形成懸空面，同時上黏下砂的土層界面，巖土體充水時崩壁內力表現為“上重下輕、內重外輕（在同一高程內層的擠壓應力和膨脹潛勢能均大于坡面地表應力）［27］”，造成崩壁不穩而有向下向外崩落的趨勢。

1.2 主要數據來源與處理

現實中尤其是夏季高溫高濕環境下，經過若干次干濕效應（亦稱干濕水平，命為Θ）交替變化，SP1土體因水分屢次進出，SP1土體的抗剪切強度τ值及其重量也隨之改變。為了在數值計算時能反映這種現象，將現場采集的崩壁原裝土樣搬回實驗室做不同程度的浸水或風干處理，共設置6種Θ。不同Θ 對應的崩壁各土層含水率ω通過鋁盒法測定（見表1），各層次土體在不同含水率ω下的重度γ可由γ＝ρdg（1＋ω）求出，土壤干密度ρd 由環刀法標定（見表2），不同ω 下的黏聚力c、內摩擦角φ值通過應變控制式不排水剪切試驗獲取（如表3）。因碎屑層在地表以下采樣很困難，其各種基本參數均無法通過試驗獲得，但考慮到碎屑層礦物成分風化較弱，相互結合較緊密，保持花崗巖原生紋理構造，碎屑層以下為球狀風化花崗巖基巖層，故可將該層和其下的基巖歸并為同一土層（命名為弱風化花崗巖土層，記作D*）以簡化分析。崩壁塑性破壞區一般不會出現在地表以下，本研究僅關心龕上覆土層處于極限狀態時的破壞區，因此土層D*的原始參數取值對崩壁整體研究意義不大，可假設其γ 和τ在各Θ 下為恒定值。又因碎屑層土粒的c和φ 值隨ω 的變化又很微小，故認為土層D*的c和φ 在各種Θ下不變，其取值通過參數反演并依經驗綜合判斷，最終確定分別恒取19.250 k Pa，38.140°，γ 值則列于表2。變形模量E 和泊桑比μ 則結合工程地質手冊選用合理的數值。

表1 崩壁不同土層在不同干濕效應Θ 下的含水率ω

表2 崩壁不同土層的主要物理力學參數建議值

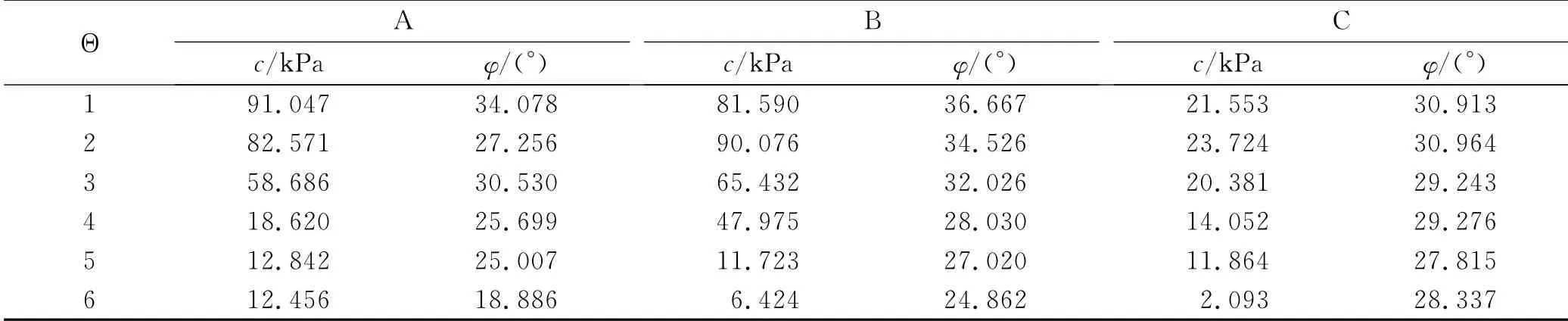
表3 崩壁不同土層的黏聚力c和內摩擦角φ

2 問題的提出、研究方法及分析模型

2.1 擬解決的問題

首先對相關概念進行闡釋。隨著龕在砂土層內沿水平方向凹陷深度d 的增加，其結果是啟動龕上覆紅黏土邊坡SP1崩坍所需能量越來越小，因此必有一個龕深值致使SP1土層恰好發生大幅度崩坍（失穩），為便于敘述，將這個龕深值命名為龕臨界（極限）深度D0（注：下標“0”非數字0，僅表示一個記號，下文可類似理解）。從另一角度試想，若龕深d＜D0時，但SP1土層的含水率高于天然含水率ω*時崩壁尚處于穩定狀態，設想繼續增加SP1土層的含水率（如遇強暴雨），因SP1土層被通過裂（孔）隙入滲的雨水弱化導致其力學特性（τ 值）連續劣化，且紅黏土吸濕增重，故也必有一個含水率值觸發邊坡SP1恰好崩落，將這個含水率值命為SP1的臨界水分含量ˉω0（ˉω0＞ω*）。

若在某T0時刻的前幾天內沒有遭遇明顯降雨，溫度也不太高（水分蒸發量可不計），則將T0時刻崩壁所處的狀態命為天然狀態（記為δ，對應Θ＝4）。對于不同d 值與崩崗侵蝕（或崩壁穩定性）之間的關系，本研究關心兩個廣義問題。①對于長期處于δ狀態的崩壁，d 為何值時崩壁會發生崩坍？龕在演變歷程中，崩壁的破壞區隨著d 的增加有何發展規律？②雖小于D0值的一系列d 值d1，d2，…，D0－1的 崩壁在ω*下未崩坍，但若虛擬增加崩壁土層的含水率ω 直到ˉω0時，崩壁可能會突然大體積解體崩塌。此問題旨在求出d1，d2，…，D0－1值下使龕上覆邊坡SP1恰好形成崩坍時與d1，d2，…，D0－1相對應的ˉω0（ˉω0＞ω*）。

2.2 擬采用的基本求解思路與方法

（1）問題1。將崩壁所有土層的ω 取為各自的ω*，隨機取若干龕深d1，d2，…，d0－1，d0，d0＋1，…，dn組成｛dn｝，滿足Δd＝di－di－1＝0.50 m（i＝3，4，…，0，…，n）且d2＝2.00 m。為模擬現實中龕的孕育是從坡面邊緣開始的，限定d1值的計算（式（1））中龕的圓弧上切點是從紅土層與砂土層的接觸線與坡面的交點起算。隨著砂土層被水蝕風化程度的增加（表現為d 值變大）龕向砂土層內部擴展的過程利用Abaqus軟件接觸對算法中的“生死”單元功能呈現（詳見圖2）。具體操作過程中，軟件將欲開挖掉單元的剛度矩陣乘以一個無窮小因子，則單元荷載變為零，從而不對荷載向量生效［29］。主要計算分析步設置如下：在Initial初始分析步后添加Geostatic分析步，并規定允許的位移容限進行初始地應力平衡，計算崩壁在自身重力下的彈性變形和應力作為初始狀態；之后在Geostatic步后插入n個靜力通用Remove分析步r1，r2，…，r0－1，r0，r0＋1，…，rn，分別開挖（“殺死”）圖2的r1，r2，…，r0－1，r0，r0＋1，…，rn區域，以實現龕深逐步增加的動態歷程。當Abaqus／Standard提交作業后計算進行到某一開挖步r0時，塑性變形范圍或屈服區從內部連通，就認為此時崩壁已崩塌，但分析步r0－1塑性區并未貫通，就認定分析步r0對應的龕深d0為龕的粗略臨界深度。若計算進行到分析步rn結束時塑性區還未連通，則需在rn后插入一系列開挖分析步并重新試算；如r1結束后塑性區就已貫通，則需在r1前插入一系列開挖分析步試算，但此時龕末端圓弧須改為普通弧線，等差Δd須作相應減小。

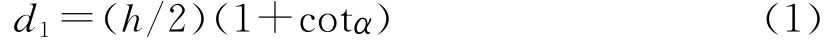
式中：h——龕的高度（m）；α——崩壁的平均坡度（°）。

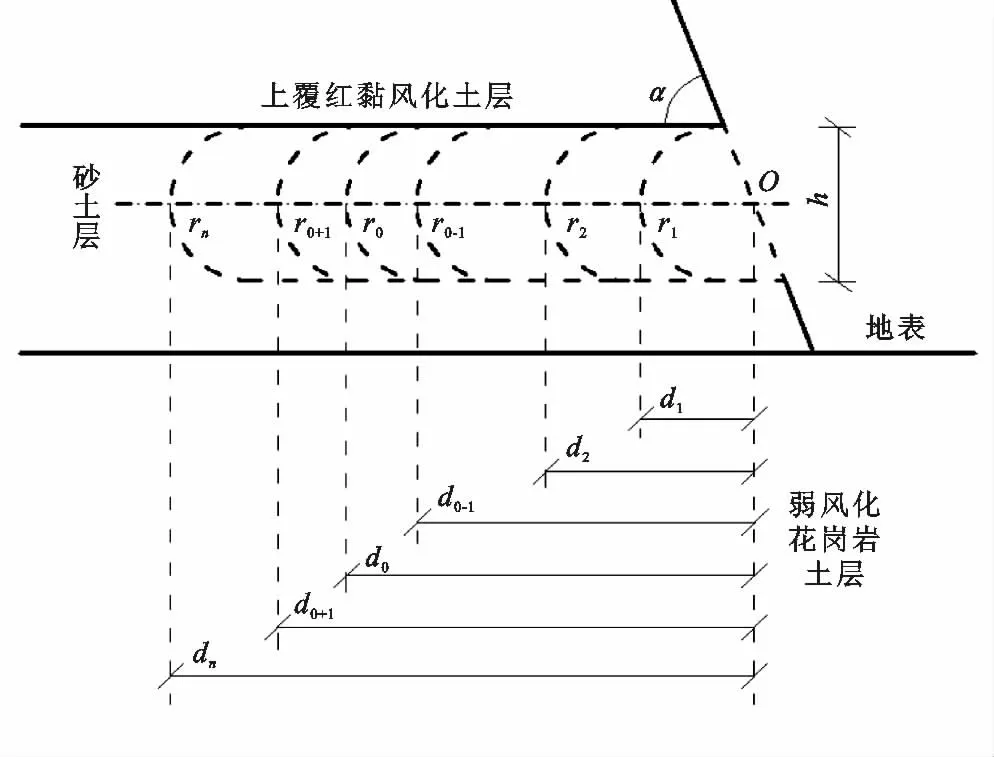
圖2 分步挖除（殺死）動態過程模擬（生死單元）法示意圖

為了提高D0的求解精度，設｛dn｝中d0的緊鄰上一個龕深為d0－1，應用計算數學“二分法”的思想，取d⊕＝（d0＋d0－1）／2。在開挖步r0－1之后，分析步r0之前另插一個開挖步r⊕（對應d⊕），查看龕深為d⊕時塑性區是否連通，如是，在區間（d0－1，d⊕］用二分法重復上述步驟；否則在（d⊕，d0］上用二分法重復計算，直至絕對誤差限（距離）ε＝｜d0－1－d⊕｜或ε＝｜d⊕－d0｜小于1.250 cm 時停止計算，由于“二分法”總是收斂的，此時對應的d⊕值就定為龕精確的臨界深度D0。筆者將以上算法叫做思路1。

（2）問題2。在問題1求解終止后，為敘述方便，假設算出的D0為D0δ，預取小于D0δ的m 個d 值構成數列｛dem｝，并任取尾項dem使其接近D0δ，且｛dem｝滿足Δde1＝dei－de（i－1）＝0.50 m（i＝6，7，…，m）。首項de1＝0.00 m 且Δde2＝de（i－1）－dei＝－0.25 m（i＝2，…，5）。之所以在｛dem｝中設2個不同的Δde，是由于現實中d 的目測值一般小于1.00 m，在［0.00，1.00］上適當加密龕深計算點更符合實際。當在｛dem｝中取某一值如1.00 m 時，在δ下崩壁未崩坍，但在雨水通過表土層下滲過程中紅黏土層的ω 會逐漸增加，若ω 繼續增大至某一值ˉω0時，崩壁塑性區剛好貫通而達到極限破壞狀態。再人為預取若干含水率ω1，…，ˉω0－1，ˉω0，ˉω0＋1，…，ωm組成新數列｛ωm｝。其中，等差Δω＝ωi－ωi－1＝0.50%（i＝2，3，…，m），且ω1取比ω*稍大的任意值?ω1。計算中令砂土層與土層D*的含水狀態恒定在Θ＝4（依據是：砂土層和紅土層交界線附近入滲系數明顯小于SP1土體的入滲系數，在崩壁剖面紅土層偏下部存在一弱透水層［30］，故在暴雨作用下SP2的含水量變化微小），只增加紅黏土層的ω，直至ˉω0時崩壁崩坍，運用二分法求出與龕深為1.00 m 對應的臨界含水率ˉω0（使允許誤差限ε 在0.05%內）。對于｛dem｝中的每一個dei值按上述方法都能求出相應的ˉω0，將求解數據用平滑曲線連接，觀察dei與ˉω0之間的變化趨勢，并擬合出二者之間的函數關系式ˉω0（dei）。為計算方便，不計同一土層在各個方向上的含水率變化梯度gradω（x，y）。

2.3 有限元模型的建立

崩崗與一般滑坡類似［4］，崩崗侵蝕關鍵因子分析可參考邊坡、泥石流等較成熟的定量研究方法［31］。參照前人崩崗模擬的做法［32］，本文作者視崩壁為一理想化的邊坡，為節省計算資源，采用二維數值模擬技術，按照崩壁實際地層的分布情況，利用Abaqus建立如圖3所示的崩壁崩坍前概化實體模型，為方便計算，將坡面簡化為直線。固然崩崗崩壁不是無限長，但對于離開崩崗兩端面相當遠的剖面受端面的影響可不計，且由于崩壁形狀沿一定長度范圍內無明顯起伏，故可按平面應變問題進行分析計算，上述簡化方式可獲得精度意義下的解答。考慮到邊界效應會對計算精度帶來影響，根據Saint-Venant原理，計算域范圍取崩壁坡腳處向右延伸1倍崩壁高度H，坡頂左延1.5H，模型上下邊界相隔2.0H。數值模型中大部采用4節點CPE4四邊形完全積分等參網格單元形式，龕所占區域采用3節點CPE3三角常應變單元進行局部加密。巖土體采用經典莫爾—庫倫彈塑性本構模型，邊界條件為：模型底部二向約束，左右側法向約束，地表及崩壁頂面無約束。

為進一步簡化，結合實地踏勘情況，對崩壁－龕模型進行了如下必要的合理假定：①各土層等厚、連續、且為彈塑性各向同性均質體；②土層之間交界面單元的c和φ 相同，且崩壁各層既不互相脫離也不相對滑動；③將溫度變化導致各土層力學性質的異變性歸結為模量E 的差異［33］，計算中不考慮裂隙的影響；④龕末端圓弧與紅土層和砂土層的交界面相切（如圖2）；⑤不計地下泉水對崩崗底部的侵蝕作用。

3 計算結果與分析

3.1 龕的臨界凹陷深度D 0 分析及因素敏感性評價

3.1.1 “開挖模擬法”數值算例、D0分析 以1.1節中所描述的處于δ（Θ 為4）下的崩壁剖面（幾何參量為：H 為7.5 m，α為70°，h為2.0 m）為例，闡明利用“開挖模擬法”求D0的明細。崩壁巖土體的破壞區范圍及位移隨著d 的增加也隨之改變，通過觀察不同d下崩壁塑性屈服區的貫通過程圖及位移等值云，可了解砂土層被淘空到一定進深時崩壁崩坍面的位置及土體單元破壞后的狀態。

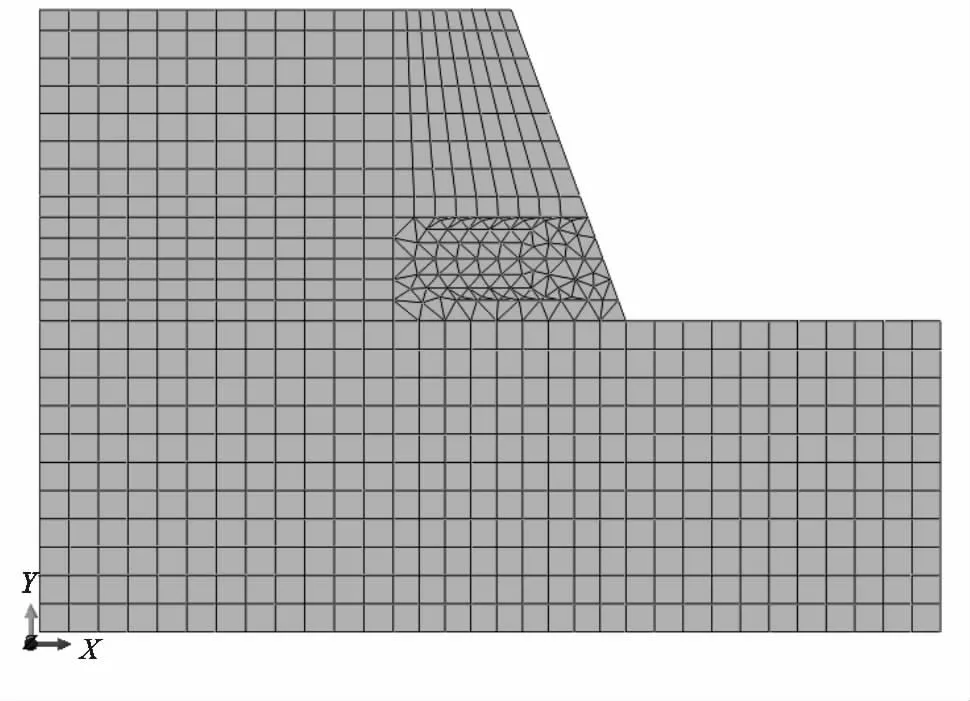
圖3 崩壁連同龕二維整體模型及網格剖分

等效塑性應變與屈服區分布情況隨著d 增加產生動態變化，塑性區與屈服區的發展變化情況基本同步。由Abaqus等值云得知，在龕形成過程中，土體單元首先在崩壁坡腳出現剪應變集中；當d 發展到3.50 m 時，隨d 的增大，在后緣（即坡頂）開始出現以拉張為主的屈服破壞區；當砂土層被水蝕至4.00 m，后緣屈服區斜向下延伸，同時坡腳屈服區也在向上擴展，兩部分屈服區連通直至形成貫通帶，表明此時控制性結構面已逐步貫通，崩壁已達到臨界破壞狀態，龕上覆土體崩坍啟動，崩坍后的產物將堆積在坡腳成為崩積堆（由崩坍后的變形網格圖可知）。綜合此時的應力云，崩壁頂部全是拉裂破壞區，意味著在野外會加速垂直縱張裂隙的產生，而坡腳形成壓剪破壞區，龕末端位置處因砂土層被開孔受到擾動，出現極大的孔邊Mises應力集中，使得圓孔附近的應力與變形狀態完全改觀，這一切共同促使崩壁快速形成滑移式崩坍面。同時結合計算云圖也能較清晰地評判出崩坍臨界滑裂面出現的大體位置（由于1個在滑動面兩側附近，且連續貫通的局部屈服破壞單元集合中必然存在一個滑動面［34］，故可認為等值云中塑性滑帶的中弧線即為滑裂面出現位置）和形狀（呈直線）。

由以上結果可理解崩壁崩落機制：坡度較大的崩壁地形陡峭，為形成崩塌奠定了基礎。砂土層風化松散，Mise應力集中，發生壓剪破壞，加之跌水作用下易坍塌形成龕，不利于崩壁穩定的結構面。在邊坡SP1自身重力和外營力作用下，裂隙易擴張貫通，崩塌受外傾結構面控制，紅黏土體重心前移，導致鎖固端逐漸破壞，使臨空土體脫離母質土而墜落。

上述計算過程是按數列｛dn｝的項數n 取7進行的，但在開挖步r7之前的分析步r6迭代進行到t＝0.959 9時，有限元迭代計算已不收斂，即崩坍面特征點位移有無限增長趨勢，而Remove步r5迭代結束時屈服區未貫通，說明龕深極限值D0不大于r6對應的龕深d6＝4.00 m，故考慮在d∈（3.50，4.00］上反復運用“二分法”查看開挖到區間中點的龕深d⊕時對應的屈服區是否貫通。逐步鎖定精確值D0所在的區間，直到搜索出滿足研究需求精度ε的D0時停止計算，最終求出該算例龕的D0值為3.68 m（為偏保守預測D0，此處四舍五入時逢五不進一）。

為更準確地剖析d 對龕上覆危巖體穩定性的影響程度，凡｛d7｝中已有的d 值以及用“二分法”求解過程中牽涉到的d 值，筆者對每一d 值都單獨建模，應用有限元強度折減法計算相對應的崩壁穩定性系數Fs，其結果匯總于表4。當d 為3.688 m 時Fs→1（崩壁到達極限狀態），從而檢驗了“生死單元法”求解D0的科學合理性。將表4中數據點在坐標紙中描點發現，Fs與d 之間服從很好的線性負相關規律，采用最小二乘法得到二者之間存在形如Fs＝2.043 3－0.279 2 d 的擬合表達式，若另Fs＝1.000 可得出d＝3.737 m，取D0＝3.73 m，與上述得出的3.68 m 比較接近。這里須要指出，現實中砂土層幾乎不可能被掏蝕如此深才崩坍，而是強降雨時邊被掏空，在下次陰雨連綿時邊形成崩坍，崩坍后d 趨于零，砂土層重新被掏蝕。由此看來，D0≈3.70 m 似乎與實際有出入，但以上計算是在未考慮降雨條件（即自始至終都處于δ狀態）下分析的。

表4 崩壁的Fs 與龕凹陷深度d 的關系

3.1.2 影響崩壁崩坍或崩崗侵蝕的因素主次分析 正交試驗設計是一種可以研究多因素多水平條件的重要設計方法，可挑選少數具有代表性的組合處理進行試驗，具有均衡分散性（在空間直角坐標系上均衡排列，不偏不倚）、綜合可比性等優點［35］。本文在研究不同d 與崩壁崩坍的關系及其敏感性因素時，遵循“盡量少選因素和水平、考慮對試驗指標影響大的因素、在不增加試驗次數前提下，可多選因素少選水平”的原則，經全面考慮，最終確定H，α，h 與砂土層厚度之比（命為h＾）及Θ作為本正交試驗的4個試驗因素，依次以A，B，C，D 表示。通過多次野外調研和地質分析成果知，δ狀態下，通城五里社區H 一般集中在7.0～9.0 m，啟動崩壁直線狀崩坍失穩所需的α約在60～80°（當α＜60°，崩壁失穩時產生圓弧狀滑裂面，本研究不考慮此情形），h＾的目測值一般在0.52～0.80，并將供試土樣通過浸水處理使Θ 控制在合理范圍內。選取的試驗因素水平（表5），研究因素A 時假設各土層厚度隨H 改變按原各土層厚度之比均勻變化（如H為8.5 m 時，表土層厚為（0.5／7.5）×8.5 m。

因上述各因素的水平數都相等、因素間交互作用均可忽略且易量化，滿足選用4因素3水平標準正交表L9（34）進行設計的基本條件，正交試驗方案如表6。在表6中9種試驗條件下，根據“開挖模擬法”，D0的計算值統計于表7。可以看出，在選定的正交組合范圍內，使崩壁恰好形成崩坍的D0在區間［0.005，5.172］內變化，在δ 狀態及風干或高溫失水狀態（Θ為3）下D0較大，但當龕上覆土層略微增濕（Θ 為5）時，D0迅速減小。

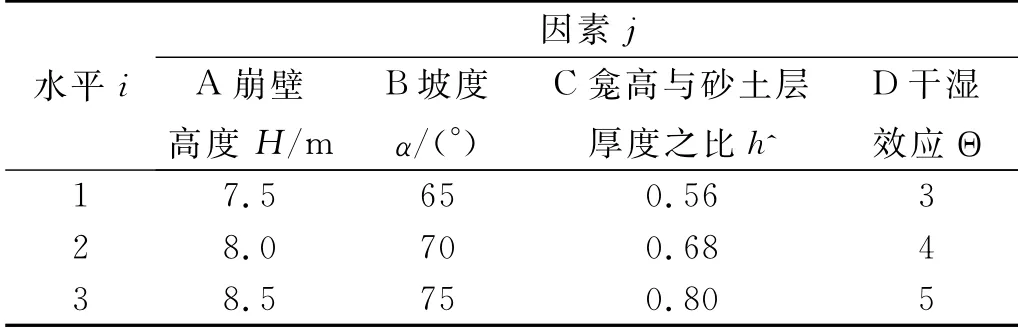
表5 試驗因素水平表

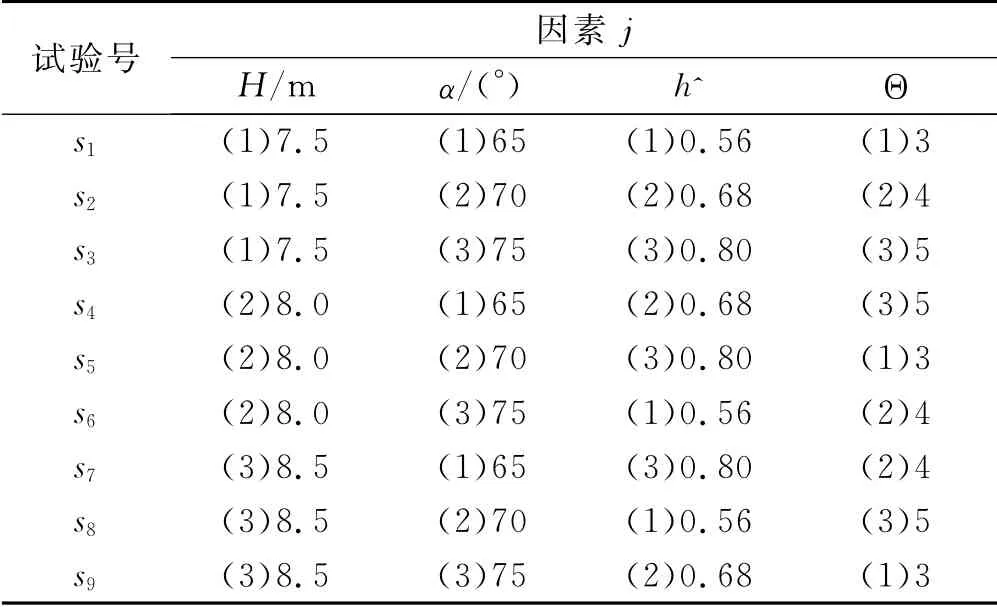
表6 正交試驗方案

表7 各正交有限元方案下龕深極限值D 0 的計算值匯總

處理正交試驗結果一般通過R 法來綜合評判因素的主次和最優組合，用R 法進行數據分析直觀形象、簡單易行。一般地，命Yji（j＝A，B，C，D，i＝1，2，3）為第j 因素i 水平所對應的試驗指標（本文即指D0）之和，ˉyji為Yji的平均值。ˉyji的大小反映了因素j的i水平對試驗指標的影響程度，據此可判斷j因素的優水平，各因素優水平的組合即最優組合。命Rj為第j 因素的極差，其計算式見式（2），Rj表征了第j因素水平變動時試驗指標的變動幅度，Rj越大，說明該因素對試驗指標的影響越大，因此也就越重要。Rj最大的因素可認為是最主要的因素，反之是較次要的因素，于是依據Rj的大小可以進行因素敏感性分析。分別對表7中9組試驗D0的求解值進行R 法計算和判斷（如表8）。

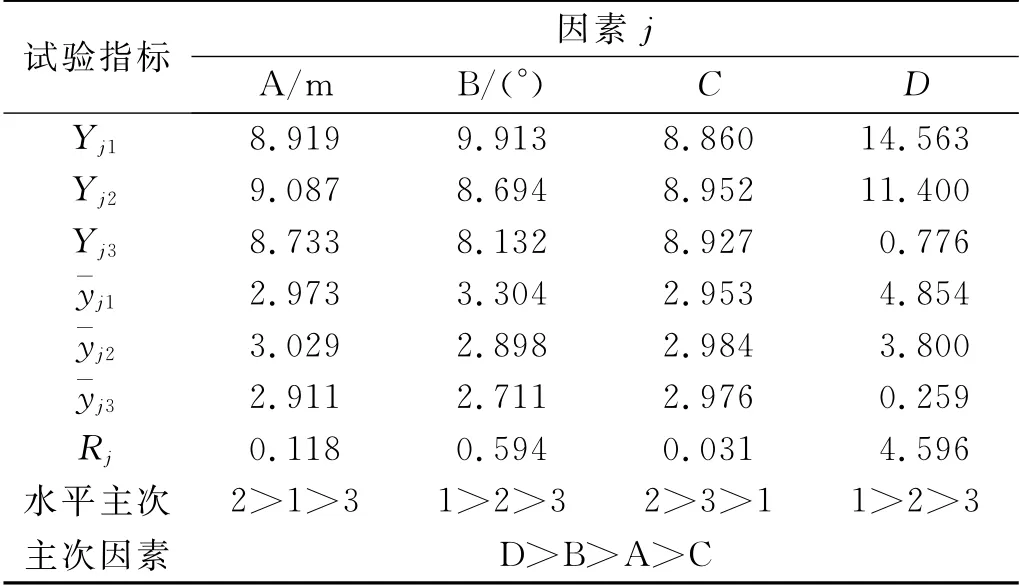
表8 多因素敏感性R 法分析結果

為更直觀明了地揭示各試驗指標Yji隨各因素水平i的變化規律，現以i為橫軸變量，Yji為縱坐標，繪制因素與指標趨勢圖（參見圖4）。

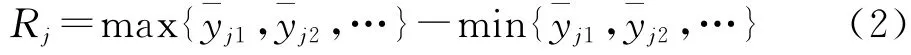
通過比較各因素的極差Rj可以得出，4因素對試驗指標D0的影響程度由大到小依次為D，B，A，C。Θ的變動造成崩壁穩定性受龕深d 的影響程度遠大于其他因素，是最顯著的影響因素，而Θ 明顯增加往往是由于雨水入滲引起的，故崩壁崩塌多發生在集中強降雨期；α對D0也有較大的影響，H 的影響程度較小，而h＾的變動對D0影響最小或者說幾乎無影響。從主次水平分析，崩壁土體含水量和坡度越小，龕上覆土邊坡SP1穩定性受d 的影響也越小，這是符合常理的；但H 和h＾卻存在這樣的一個臨界值（奇異點），使崩壁啟動崩坍所需d 的最小值最大（見圖4）。究其可能原因，當因素C 取值較小（h＾小于0.68）時，雖然龕的體積較小，但龕進深最大處孔端Mises應力集中較大且占主導地位，導致邊坡SP1穩定性降低，致使崩壁明顯崩坍的D0相對較小，試想若命h＾→0，則龕的存在相當于一細微裂紋，根據Griffith 強度理論，材料的破壞往往始于裂縫端，而崩壁土體受力后使裂紋尖端附近應力明顯升高，這對龕上覆土體強度和穩定性極為不利；當h＾達到0.68（即因素C 的2水平）時，孔端Mises應力減小，D0達到極大值；當h＾繼續增大，雖Mise應力集中現象繼續減弱，但此時龕體積較大（龕上部臨空面相對零勢面的重力勢增大）且居主控地位，換言之，龕體積的增大引起D0的減小值掩蓋了Mise應力效應減弱引起D0的增大值，故D0反而減小。根據常識H 越大就越不穩定，但模擬試驗結果表明，H 也存在一個使崩壁穩定性受龕深d 影響最小的臨界值，筆者認為當H 增大時，砂土層的厚度也在增大，在h＾一定的條件下，從而h 也在增加，可見研究因素A 時不能單純從崩壁高度角度解釋，還應考慮h變化導致Mise應力效應變化對D0的綜合影響。綜上所以，因D0（或ˉyji）越大崩壁崩坍的概率就越小，故四因素優水平的組合便是本試驗的最優組合A2B1C2D1，即崩壁最穩定狀態。若命組合A2B1C2為最穩定條件IF，可以計算，在同時滿足條件IF和崩壁Θ 為3的附加約束條件下，D0的理論值為5.295 m。

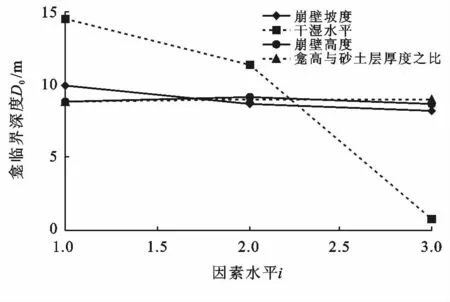
圖4 因素水平與龕侵蝕臨界深度趨勢間的關系

3.2 觸發崩壁崩坍的臨界水分含量分析

研究問題2需用到紅黏土層的c，φ 值與土含水量ω 之間的映射關系，由于只對很有限的6種Θ 下土層的抗剪強度τ值進行了實測（詳見表3），仍無法滿足科研需求。若用Excel表格擬合c，φ 與ω 之間的算子關系，不僅擬合的函數式有時光滑度較差（不能保證二階導數連續），甚至在某自變量取值區間上目標值與真實值偏差較大，故在浸水試驗有效數據基礎上，可采取插值法手算，將有限的離散實測值變換為一連續的能描述c，φ 值與水分含量ω 之間關系的定量表達式，這樣任取一較高的ω 值帶入表達式求出對應的τ 值，并將其植入ABAQUS軟件中便可模擬龕上覆土層吸水連續軟化的真實狀態。

因崩壁剖面各土層的ω 隨時間空間改變而改變，而本文僅對通城縣某一地理坐標的崩壁展開研究，加上影響崩壁崩坍因素的復雜性與不確定性，成果未必很好地適用其它地域的崩壁，故若將表土層和紅土層在6種Θ 下的ω 用式（3）轉化為各自的飽和度Sr顯得更有實際意義，換言之，問題2的著落點轉移到探索觸發龕上覆紅黏土崩塌所需的臨界（最小）飽和度S*r0在什么范圍內，似乎價值更大。為此，命表土層A和紅土層B的飽和度分別為SrA，SrB，當雨水下滲到SP1土層時，在同一Θ 下SrA與SrB并不等，在求解問題2時是以SrA為準還是以SrB為準呢？注意到表1中紅土層與表土層在同一Θ 下的ω 差別不算大（故猜測Sr也差別不大），可對兩土層的飽和度取平均進行簡化處理，命土層A 和土層B 按土層厚度加權的平均（或整體）飽和度為S*r（按公式（4）計算），計算結果如表9所示。為節省篇幅，文中僅以條件IF（H 為8.0 m，α為65°，h＾為0.68）為例分析問題2。在條件IF下，當崩壁處在δ狀態時，應用“開挖模擬法”得出D0δ（為避免前后混淆，將此處的D0以符號D0δ代替）為4.119 m，固定若干小于D0δ的龕內蝕深度dei，探索在降雨天氣下SP1土層吸濕增重時的S*r增加到何值時崩壁突然啟動大幅度崩坍。

式中：n——孔隙率（%）；ρw（取為1 g／cm3）——純水在4℃的密度；hA，hB——表土層和紅土層的厚度（m）。

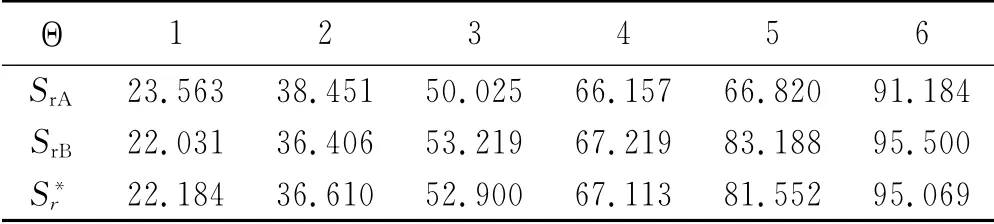
表9 龕上覆紅黏土層的平均飽和度S*r 與Θ 的關系 %

下面以強度指標c和φ 值為因變量，紅黏土層的S*r為自變量，求4個簡單插值多項式近似替換表3。為避免舍入誤差積累帶來的病態問題，在進行插值計算時至少保留小數點后五位。由于只研究龕上覆土邊坡吸濕增重過程中飽和度的變動對崩壁崩塌的影響，并不考慮自然蒸干過程中水分含量降低對崩壁穩定性的影響，故而忽略Θ 為1，2的情況，但為保證可靠度，保留Θ為3的情形，并取S*r3＝0.529 00，…，S*r6＝0.950 69為插值節點。對Θ 為3～6下的S*r與表3中相應的表土層粘聚力cA進行3次拉格朗日插值（公式（5）），同理，得出紅土層黏聚力cB與S*r的3次Langrange插值多項式（式6）。從表3 可知cA應為S*r的減函數，但對式（5）求一階導發現cA′（S*r5）大于0（≈13.615），在插值點S*r5附近的鄰域δ（S*r5）內及區間（S*r5，S*r6）上式（5）嚴重失真。通過進一步求導得出cA′（S*r4）≈－127.3，并觀察到在區間［S*r5，S*r6］上cA變化很小，故可另cA′（S*r6）＝0作為第一類邊界條件，在區間［S*r4，S*r6］上進行三次分段樣條插值以保證所求分段多項式二階導數連續可微，結果見式（7），可驗證，式（7）具有很好的適用性。用類似方法得出cB與S*r的樣條插值函數式（8）。對Θ為3到6下的S*r與表3中的表土層內摩擦角φA 進行3次牛頓插值（式（9）），同理，得出φB 與S*r的3次Newton插值多項式（式10）。公式（9）和（10）的精度能得到滿足本文近似程度要求的結果，無需再進行樣條插值，在不同的S*r下SP1土層的容重γ按式子（11）計算。至此，有了公式（7）—（11）就可以在［S*r3，S*r6］上?S*r，求出其對應的所有計算參數，從而可分析該飽和度下崩壁當前的穩定程度或崩坍的幾率。下面將計算數列｛dem｝中各數項dei對應的使SP1崩坍的臨界飽和度S*r0。

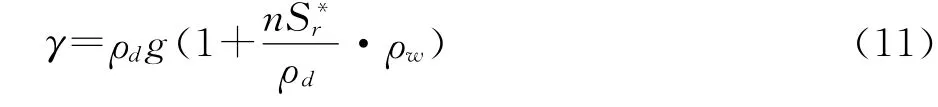
鑒于前文算出的D0δ為4.119 m，故取｛dem｝的項數m＝11比較理想，令尾項de11為4.00 m 以使其靠近D0δ。求解方法沿用求解問題2的思路2，只是將｛ωn｝換成S*r組成的數列。但判斷崩壁崩坍（失穩）的標準不是沿用“單元生死法”塑性區是否貫通，而是利用有限元強度折減法，計算某一龕深dei（i＝1，…，11）下的崩壁在紅黏土取不同飽和度S*r時的Fs，若某次試取的S*r使Fs接近1，則采用“二分法”思想，縮小S*r的取值范圍繼續試算，直至試取的S*r使Fs無限逼近于1且誤差限不超過0.05%，則認為該龕深度dei下的崩壁恰好形成崩坍，此時的S*r即為所求的臨界飽和度S*r0。限于篇幅，表10只給出了計算結果。命（S*r0－S*r4）為邊坡SP1相對天然飽和度S*r4的增量臨界飽和度ΔS*r0，ΔS*r0＞0對應紅黏土降雨期吸水軟化，ΔS*r0＜0對應紅黏土水分蒸發。為更準確地發現自然規律，現利用表10中的數據點以及之前算出的數據點（4.119，67.113）和（5.295，52.900），繪制條件IF 下龕上覆土層的平均臨界飽和度增量ΔS*r0與dei的擬合關系曲線，結果如圖5所示。

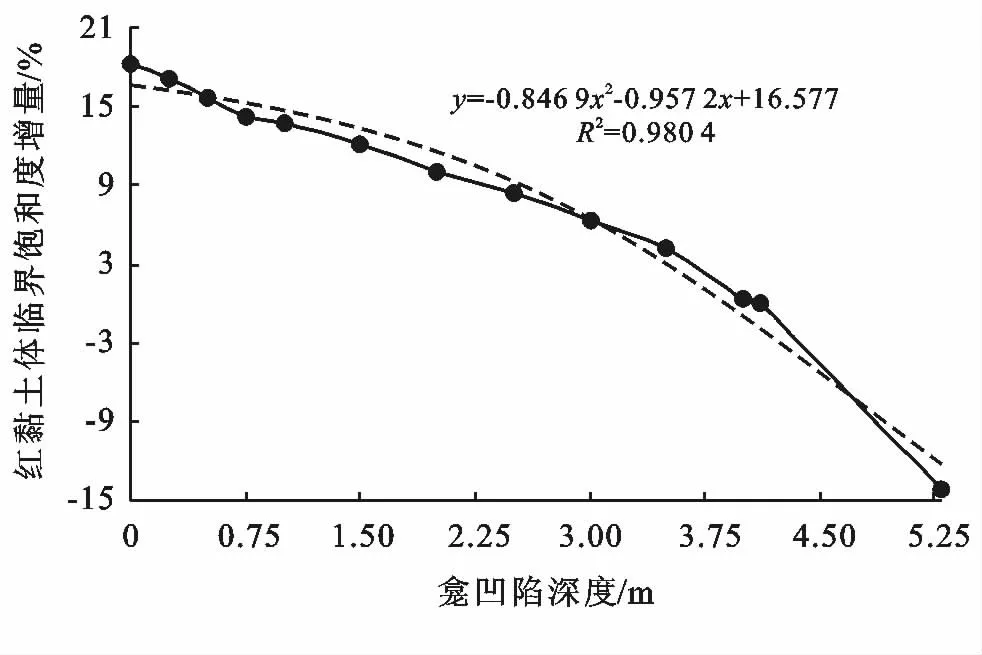
圖5 龕上覆土層ΔS*r0隨dei的變化規律（命為崩坍預測跡線）

表10 ｛de11｝中龕深度dei與龕上覆邊坡土層S*r0的映射關系

據任兵芳等［10］對龕形態資料的記載：通城縣五里鎮和程鳳村龕深觀測值分別在0.02～0.45 m 和0.20～1.00 m 范圍內，由于H 及h 對崩壁崩坍事件發生的影響程度相比d 而言很小，故可近似認為致使通城崩壁形成崩坍的S*r0與H 和h 無關，也就能使得以采樣點處的崩壁為研究對象所得的結論可近似適用于通城縣其它地理坐標類似地質環境下的崩壁。將龕深觀測值代入圖5 中經驗擬合公式ΔS*r0≈16.577－0.957 2dei－0.846 9d2ei，可得到五里鎮和程鳳村α在65°附近的崩壁，其臨界飽和度預測值的區間范圍分別為［83.088%，83.671%］和［81.886%，83.465%］。對于非65°的崩壁可按思路2提供的算法重新推導對應坡度下的臨界飽和度經驗公式，并可重新對S*r0的大致范圍進行估算。

4 討論與結論

4.1 結果討論

4.1.1 對問題1與問題2的幾點反思及討論 查看圖5中曲線的走勢，龕深與ΔS*r0近似滿足二次函數變化規律，且顯著負相關（其擬合決定系數R2為0.980，表明龕深與ΔS*r0之間的函數關系式真實存在）。由此可推出龕越發育（即dei越大）崩崗發育越快（圖5中曲線斜率在增長，即SP1的飽和度S*r與致使崩壁崩坍災害發生所需的極限值S*r0之間差值的絕對值的減小速率在增加），這與任兵芳［10］等人研究結果一致。

設某地按時間先后順序遭遇N 次降雨，每次降雨總量依次命為Q1，Q2，…，QN。既然龕的形成與擴大由降雨或爆流引起［36-37］，而崩崗壁的大量崩塌也是在強暴雨期土體飽和度增加、增重和軟化等一系列過程后發生的［24］，那么崩壁在經歷一次降雨過后，究竟是發生龕的擴大還是啟動崩壁崩坍呢？問題2的解答提供了一種有理論支撐的回答：若一次降雨過程使得邊坡SP1的飽和度S*r達到或超過對應此龕深的S*r0，它將發生崩坍；反之，倘若一次降雨量Qi（i＜N）沒有使得SP1的S*r達到S*r0，則它將促使龕的萌芽或d 值增加（崩壁不會啟動明顯崩塌，但可能會有坡面淺層土體局部流滑）。而龕擴大的結果使得崩壁的Fs降低，就意味著下次促使崩塌的臨界雨量Q（i＋1）0（或臨界飽和度）小于之前與使龕擴大相對應的臨界雨量Qi0（Qi＜Qi0），若Qi＋1還沒達到Q（i＋1）0，則結果是d 繼續加大，Fs繼續下降。如此反復，直到d 達到某一較大值，相應的臨界雨量達到一較小值，此時SP1也許稍微吸水（雨量不大）就會發生崩塌。這種思考提醒我們，因龕形成的危害小于崩壁崩塌的危害，若某崩壁龕的形態用肉眼能明顯識別，那采用填充龕的方式就意味著提高了SP1的極限飽和度（或雨量閾值），間接降低了其崩坍破壞的可能性。

在強降雨或持續中小雨環境下，命崩壁崩坍為事件1，龕的孕育或龕深d 增加為事件2，事件1與事件2發生的概率分別為P1，P2。若假設一場強雨過后，事件1與事件2對立，且事件1與事件2發生足夠長時間后崩壁處于δ（即含水狀態恢復到Θ 為4），則每逢降雨時事件1或事件2的發生與否，完全取決于相應的龕深下降雨后紅黏土體的S*r是否從天然飽和度S*r4增加到臨界值S*r0。在侵蝕龕未出現前，強降雨時因雨水入滲量及紅黏土吸水有限，S*r一般達不到de1＝0.00 m 對應的臨界值0.853 29，P1幾乎為0，P2幾乎為1，換言之，崩壁只有先出現龕等微地貌再崩坍。若下次雨強還未使紅黏土壤的飽和度達到相應龕深下的臨界值（此臨界值小于龕未出現前的飽和度臨界值），則事件2發生，d 加大。d 加大的結果是S*r0越來越小，且減小速率也在增加（對圖5中的預測曲線擬合式求導便可知），這意味著以后的降雨中P1越來越大，P2越來越小，即崩壁崩坍的幾率快速增大，直到某一次降雨使事件1 發生，發生的結果是SP1崩坍后龕深重新歸零。重復上述步驟，如此循環不息，最終結果是致使崩崗進一步發育，這與任兵芳等［10］的論斷“龕的不斷形成（對應龕深增加）致使溯源侵蝕（對應崩壁穩定性降低直到崩坍形成，進而龕消失）最終導致了崩崗發育”相吻合。

以上分析在一定程度上緩解了問題1中計算的D0可達3.50～5.30 m 的矛盾，而如此深的龕在現實中是找不到的。問題1 的解答是在一種長期處于δ狀態或（半）干旱狀態（Θ 為3）的理想狀態下分析的，而現實中崩壁土體一般是處于干旱—δ 狀態—近飽和交替變化的環境，崩崗發育的過程也是崩壁邊形成龕邊經歷崩坍的過程，故現實中所看到的龕深一般較小（屬0.3～0.6m 范圍）。從廣義問題1 的研究分支—正交試驗結果來看：當SP1的含水率ω 從ω*開始增加（Θ由4變到5）時，D0明顯變小，即崩壁土體稍一濕潤就可能引發崩坍破壞，這符合崩壁崩塌多發生在接連降雨期的一般事實；據圖4，坡度與崩壁高度對崩壁穩定性的敏感性程度相比，明顯是前者高于后者，這與季翔等［20］研究結果（崩崗侵蝕溝外擴主要受坡度的影響，坡面高度的規律性較低）相容。綜合表7和圖4可知，D0與土體含水狀態密切相關，這也解釋了崩壁常出現陰雨連綿時大量崩坍的特征最為重要的原因。顯然，做好排水措施，減少集雨面積以減少雨水的下滲對穩定崩壁有重要意義。

總而言之，若沒有前幾次降雨在崩壁土體中使龕規模擴充的累積效應，一次降雨后紅黏土層平均飽和度S*r很難達到無龕崩壁啟動崩坍所需要的最小飽和度。伴隨著降雨持時的增加或降雨間隔較短時，S*r的實時值S*r（t）與S*r0的差值有所減小，而崩壁土體中在一次降雨前初始含水量的多少，決定該次降雨時飽和度所能到達的峰值，該峰值與臨界飽和度的相對大小決定了崩坍的發生與否。因此，崩崗形成與前期土體含水量相關，前期降雨在紅黏土體中的水分累積效應對崩崗的發育起到重要作用，那么陰雨連綿時（即使雨強不太大）SP1土層飽和度的積累（量變）很可能會引起崩壁失穩（質變），這與王彥華［38］等觀點（若沒有前期降雨在土體中的累積效應，一次降雨的濕潤前鋒很難達到崩崗所需要的臨界深度，當前降雨之前坡體中的含水量決定當前降雨的濕潤前鋒深度，是影響坡體穩定性的重要因素）非常一致。綜上所述，前期降雨在崩壁體內具有累積效應，一方面使砂土層剝落并退去后形成龕，另一方面增加當前較深層土體的飽和度，減小抗剪強度，增加紅黏土容重并產生動水壓力，改變了崩壁的極限平衡狀態，造成了崩壁失穩及崩崗的發育與發展。

4.1.2 崩崗治理新思路 對數值結果的分析，可啟迪我們轉換崩崗治理技術：應依據龕深值及龕上覆土層的增量飽和度ΔS*r雙重指標對每個崩壁的穩定態勢進行實時預測預警，以對出現的龕能及時進行綜合處置，如對龕進行清除或用高聚物膠凝材料填充；對龕上覆臨空欠穩定土體可采取柱支撐、網攔擋、石灰土加固等聯合措施，并可結合實際制訂崩坍應急預案，唯有如此才能有效遏制崩崗的后續侵害。對于崩崗嚴重區段，在處理龕的同時也可對崩壁其他要素采取一定措施如：對崩壁斜坡面補栽植物以截流，并可配合修建谷坊、攔砂壩等措施，必要時對坡頂裂隙，可采取封閉、埋置擁有一定抗拉強度的三維復合土工格柵，以最大化降低崩崗災害的風險。

在崩崗防治工作中，實時預測其崩坍發生與否方法如下：對某次降雨后某t1時刻崩壁（α 為65°）的d進行人工量測，將量測值帶入崩坍預警公式ΔS*r0≈16.577－0.957 2dei－0.846 9d2ei，得到t1時刻的臨界飽和度預測值S*r0｜t＝t1。對土層A 和土層B分別插入濕度傳感器進行ω 的實時監控，利用式（3）將ω 的監測值換算為飽和度實時監測值，將土層A 和土層B的飽和度實時監測值按厚度加權平均得到S*r｜t＝t1，若S*r｜t＝t1接近于S*r0｜t＝t1，則崩壁在t1時刻有崩塌失穩的跡象，必須對龕及時補救以防患于未然。

4.2 結論與未解決的問題

基于ABAQUS程序及數學近似處理思想，建立有較強預測和適應能力的崩壁—龕數值模型，在此基礎上提出了與龕演化相仿的“開挖模擬法”及崩壁穩定性的定量分析方法。研究了通城縣龕深對其上覆紅黏土體穩定性的影響，并探索了一系列較小的龕深與導致崩壁崩坍時紅黏土層所理應具備的最小（極限）飽和度之間的定量關系式，且試算結果良好，得出幾點重要認識如下：

（1）崩崗崩壁坡度足夠大時，潛在崩坍面呈直線或折線狀，崩壁后緣形成拉張破壞區，易產生垂直拉裂隙。崩崗形成流程為：崩壁陡坡形成—下部土體被水蝕掉塊—龕形成—紅黏土層臨空—解體崩落—堆積坡腳—崩崗產生。

（2）龕的形態對其上覆紅黏土層穩定性的影響主要表現為深度增加對其的不利影響。崩壁在未降雨工況下一般是自穩定的，只有龕深達到一很大值時，才會啟動崩坍；而龕上覆土層含水量從天然值開始增加時，龕臨界深度驟減。

（3）崩壁高度H，坡度α，龕高與砂土層厚度之比h＾，飽和度相對天然飽和度的增量ΔS*r的變化均會改變龕深對崩壁崩坍概率的影響程度，四因素的敏感性由大到小依次排列為：ΔS*r，α，H，h＾，且ΔS*r的影響權重遠大于其他各因素。在所設計的試驗因素一定范圍內，H 與h＾的變動對紅黏土層穩定性的影響非常小，這也揭示了在預測或計算崩壁的穩定性系數時，可以忽略掉H 對計算結果的影響。換言之，可以只根據崩崗的坡度和含水量來預報崩壁當前的穩定程度。依照感性認識，對于未出現龕的崩壁，H 越大越不穩定，但龕出現后，存在一臨界高度H0使崩壁最不易崩坍，當H＞H0時，此認識才能精確成立。

（4）抗剪強度在風干和増濕階段明顯不同，插值變換公式具有較精確解析解的性質，故可根據不同土壤含水量通過插值函數式預測土體抗剪強度，進而計算崩壁安全系數，從而為評估崩壁穩定性鋪墊道路。

（5）一場暴雨后崩壁失穩與否，由降雨量是否達到使紅黏土層的平均飽和度達到極限值的門檻值決定，而崩壁后退是由崩坍引起的，故可進一步得知，降雨量越大崩壁后退就越發明顯。龕深與使具有這一龕深的崩壁恰好崩坍所需的龕上覆土體最小含水量之間呈二次函數遞減趨勢。

（6）結合有限元理論計算值，利用崩壁崩坍預測擬合公式ΔS*r0≈16.577－0.957 2dei－0.846 9d2ei，對促使通城崩壁剖面形成崩坍的臨界（極限）飽和度范圍進行了合理預測，其結果具有一定的參考意義。

風干階段崩崗巖土體的強度主要受裂隙性控制，當紅黏土體含水率極低時也會引起土強度降低，尤其是粘聚力減小較多，從而崩壁穩定性也會受到影響，故紅黏土邊坡飽和度處于低水平時龕的存在及裂隙的伸展與崩壁穩定性的關系尚待進一步深入研究，從而擴充成果的崩坍預測范圍。本文也未能解決裂隙主控結構面的存在對崩壁崩坍的影響，但考慮到龕上覆臨空土層可看做疊合構成的懸臂梁，梁的一端固定另一端自由的模式，因此龕深對紅黏土穩定性的影響規律尚待從斷裂力學和損傷力學計算方法及材料力學理論角度進一步去挖掘。此外，崩崗土體實際上并非完全均質、連續、各向同性，而由于軟件的局限性，本次有限元模擬將其看做理想彈塑性體并認為土體符合摩爾—庫侖本構，故后續有待根據崩壁土層的顆粒級配建立本構模型，采用PFC3D離散元軟件從細觀上定義顆粒之間的接觸關系也許會更好地再現崩崗坡體崩塌的全過程，進而搜索出裂紋的產生位置。