基于FLUENT的90°彎管內水環流動特性研究*

吳君強 蔣文明 楊娜 張倩 杜仕林 劉楊 陳義美 來興宇

1山東省油氣儲運安全省級重點實驗室

2中國石油大學（華東）儲運與建筑工程學院

3長慶油田公司生產運行處

4中國石油管道局工程有限公司

目前，人們對于稠油的需求越來越高，而稠油由于其黏度過高，傳統的輸送稠油方法（主要有加熱、稀釋和乳化）均存在一些問題[1]。而水環輸送不僅可以節約能量，還可以減少原油對管壁的污染，因此水環輸送稠油正受到越來越多的關注。

國內外對水環輸送高黏原油的研究最早可以追溯到20 世紀初，DOVE 等[2]最初提出可以使用特殊的油水混合裝置形成水環輸送原油。屠大燕等[3]通過對水環同心流動進行分析，發現由于管壁附近的高剪切區被低黏相的水所占據，因而流動時摩阻能大幅度下降，甚至可能實現管道輸送接近凝固點的原油。馬祥琯[4]對水環輸送的效益、水環液體的選擇、水環流量比的選擇三個方面進行了研究，認為水環輸送的經濟效益主要取決于流量增加比和能耗降低比。并且層流水環流量增加比遠高于湍流水環，因此水環輸送對高黏液體、低雷諾數流動狀態效果最好。劉天佑[5]進行了黏稠油偏心水環輸送的研究，且導出了偏心率的計算公式。該研究不僅給出了適用于任意厚度的層流水環流態判據，同時又得到了光滑區湍流水環流態判據和層流核心流態判據。JIANG 等[6]為獲得水環在Π 型管道中的流動特性，運用VOF 方法對油水兩相流進行了模擬。國外學者BANNWART[7]對水環在水平、豎直、傾斜管中均有研究，通過研究發現，界面張力在油水環狀流中起著重要的作用。GHOSH 等[8]對水環通過水平、向上和向下的U形管進行了研究，在研究條件下，U 形管在向上流動的過程中最不容易污染壁面。PARK 等[9]對彎管中的油水兩相流和單相流進行了比較，結果發現，二次流對水環通過彎管影響顯著。

由于在輸送稠油的過程中不可避免地經過彎管，且水環通過彎管時流動參數對其影響較大，而前人對此研究又較少，因此系統地研究流動參數對水環通過彎管時的穩定性具有實際意義。本文通過FLUENT詳細分析了90°彎管中不同流速、不同密度比和不同黏度比對水環結構的影響，可為將來水環的現場應用提供理論參考。

1 模型的建立

為了充分反映水環在彎管中軸向和切向的流動情況，采用三維模型對彎管建模分析。圖1為彎管結構示意圖，油相沿管道中心射入，水相沿環形區域射入[10]。

彎管的幾何尺寸為：管道直徑9.52 mm，進油口直徑7.48 mm，管道的曲率半徑28.56 mm，曲率比1/6，直管段長度20 mm。

1.1 控制方程

假設油水互不相溶，為了捕捉油水界面的位置，選擇FLUENT求解器中的VOF模型對水環在彎管中的流動進行模擬[11-12]。模擬涉及到的公式如下：

連續性方程

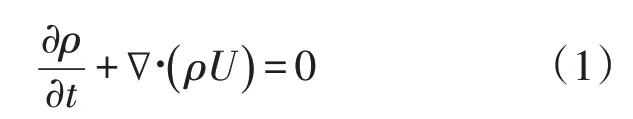
式中：ρ為密度，kg/m3；U為速度，m/s；t為時間，s。

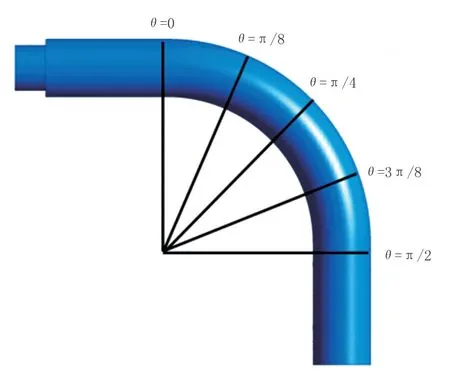
圖1 彎管結構示意圖Fig.1 Structural diagram of elbow

動量方程

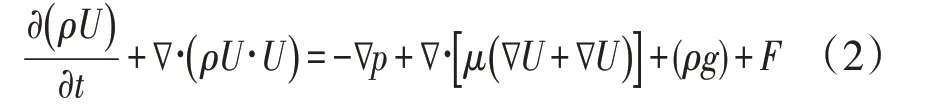
式中：p為流場中的壓力，Pa；g為重力加速度，m/s2；F為作用于系統的力，kg/(m2·s)；μ為流體的黏度，Pa·s。

標準k-ε模型的基本運輸方程為[13-14]

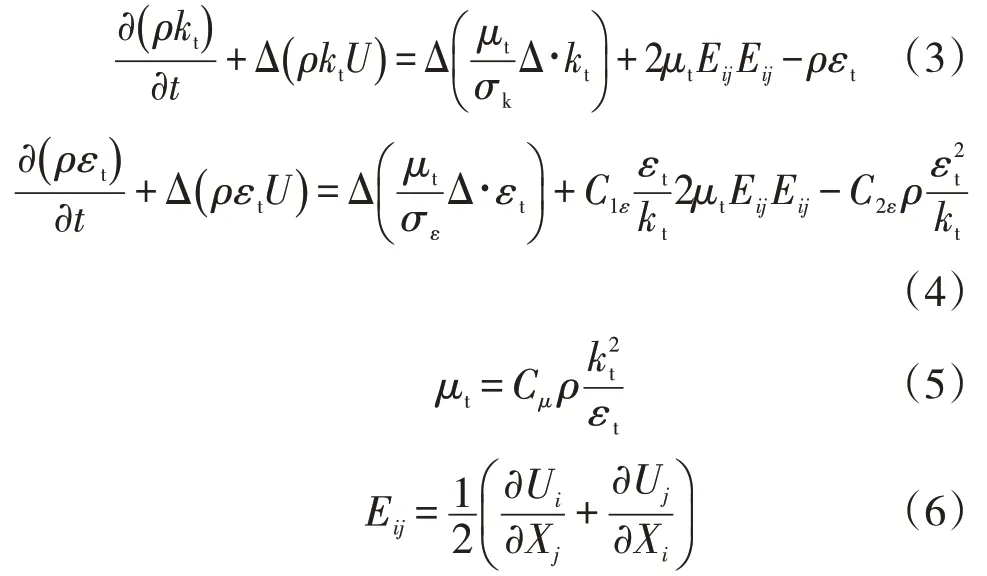
式中：kt為湍流動能，m2/s3；εt為耗散速率，m2/s3；μt為渦流黏度，Pa·s。

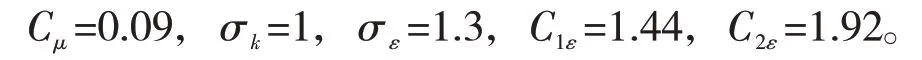
1.2 模型驗證

為驗證模擬結果的準確性，與Ghosh論文的結果進行驗證[15]。采用與GHOSH S 模型中相同的參數，觀測段長480 mm，直徑12 mm，油相進口直徑8 mm，油水速度分別為0.53 m/s和0.3 m/s，油水黏度分別為0.2 Pa·s 和0.001 Pa·s，油水密度分別為960kg/m3和1000kg/m3，模擬條件下的重力加速度g=-9.8m/s2。采用本文的數值模擬方法對其模型進行計算，實驗與模擬結果對比如圖2和圖3所示。

由圖2 和圖3 可見，采用本文的數值計算方法與Ghosh S 模型結果基本一致，油水分布與文獻中相同，壓力變化趨勢一致，誤差在20%以內。說明本文的計算結果可靠，可以用于模擬水環在管道中的流動。

圖2 稠油體積分數云圖Fig.2 Cloud chart of heavy oil volume fraction

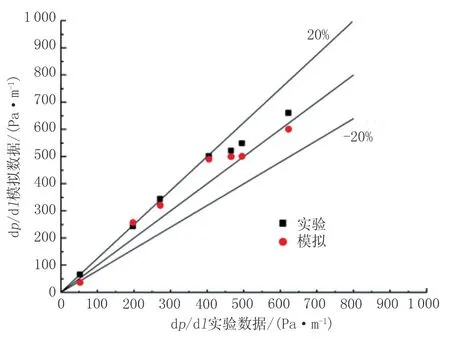
圖3 模擬結果與實驗數據對比Fig.3 Comparison between simulation results and experiment data

2 數值模擬

2.1 參數設置

研究條件下初始時刻油水入口采用速度進口邊界條件（vo=vw=0.3 m/s），出口為壓力出口（p=0.1 MPa），壁面為無滑移邊界條件。油水性質如表1所示。

2.2 網格獨立性檢驗

為了較全面地獲得彎管內部的流動情況，采用三維非結構網格對模型進行網格劃分，網格數目分別為3 219 433、3 461 662、4 527 931。如圖4 所示，為使油水界面清晰，并同時滿足網格獨立性要求，最終網格數目選擇為3 461 662。

表1 油水物性Tab.1 Oil and water properties

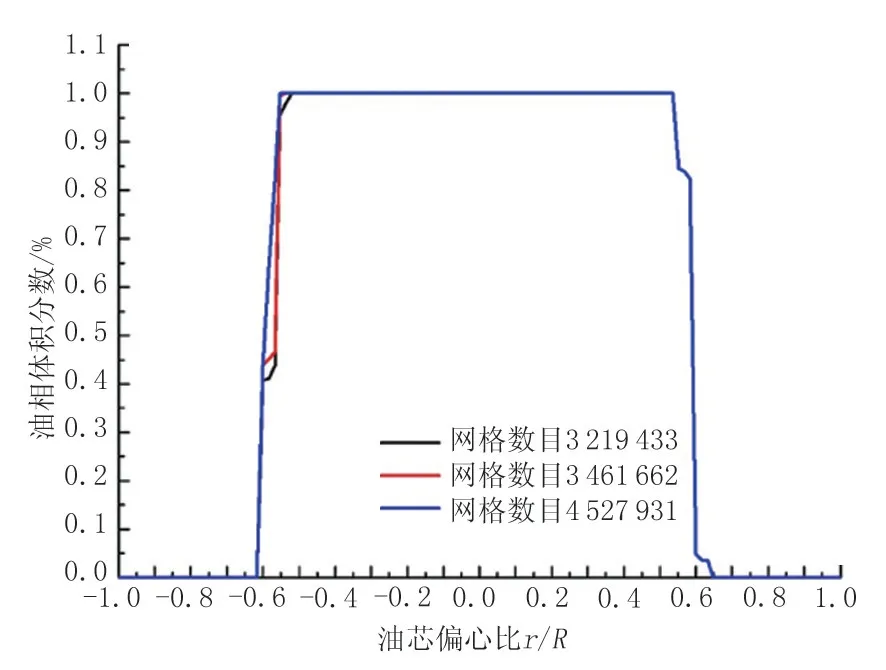
圖4 模擬結果對比Fig.4 Comparison of simulation results

3 結果與討論

水環在彎管中流動時并不能一直保持穩定流動，與水平管中不同，水環在彎管中流動時不僅受到浮力的影響，離心力對其穩定性影響也不可忽略。如圖5所示，隨著彎曲角度的增加，水環核心逐漸向管壁一側偏移，并且彎曲角度越大，偏移越明顯。因此，研究流動參數對水環在彎管中的影響具有一定的現實作用。

3.1 流速對彎管水環的影響

為研究彎管中流速對水環流場的影響，保持表面張力為0.2 N/m不變，出口壓力為0.1 MPa，忽略重力的影響，分別設置流速為0.3、0.6、0.9 m/s，分析流速對彎管中水環的影響規律。

從圖6 和圖7 可知，隨著流速的增加，核心油流向管道外側偏移程度增加。當流速為0.3 m/s時，隨著彎管偏轉角度的增加，彎管內部的核心油流仍保持在管道中心，向管壁偏轉的程度較小。當流速為0.9 m/s 時，隨著彎管偏轉角度的增加，彎管內部的核心油流向管壁偏移的程度較大，且核心油流的形狀在水層的擠壓下變形，經過彎管后核心油流保持向管壁一側偏移的狀態向前流動。其原因在于流速增大導致水環經過彎管帶來的離心力增大，水和油的密度差導致彎管帶來的離心力大小不同，進而發生核心油流偏移的現象。

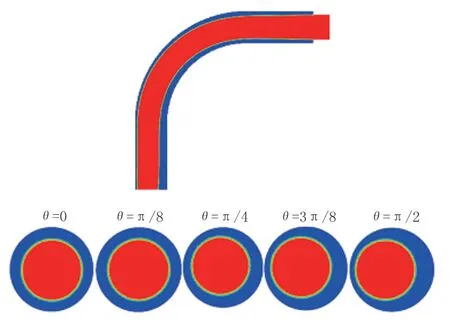
圖5 稠油體積分數在彎管中的分布Fig.5 Neavy oil volume fraction distribution in the elbow

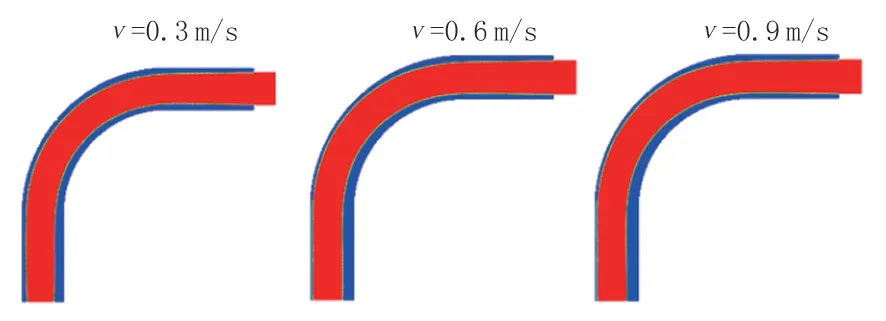
圖6 不同流速下水環在管道中的油水體積分數分布Fig.6 Oil and water volume fraction distribution of water ring oil in the pipeline under different flow rate

圖7 不同流速下水環在管道內的五個模型截面位置處油水體積分數分布Fig.7 Oil and water volume fraction distribution of five model section in the pipeline under different flow rate

3.1.1 界面油水體積分數分布

圖8為入口流速為0.9 m/s時彎管不同截面處的油相體積分數分布曲線，從圖8 中可以看出，當θ=0時，油芯主要聚集在管道的中心，隨著彎管角度的增大，水環向彎管外側偏心的幅度增大。在離心力的作用下，油相逐漸靠近彎管外側管壁。

3.1.2 界面速度分布

入口流速為0.9 m/s 時彎管不同截面處的軸向速度分布曲線如圖9所示。當θ=0時，在油芯偏心比為-0.7～0.7區域，中心油速基本保持不變，環形水層區域速度梯度很大，剪切強烈。而隨著彎管角度增大，彎管外側速度梯度增大，剪切區域變小，內側速度梯度減小，剪切區域變大。這說明在0.9 m/s流速的條件下，隨著彎管角度的增大，由于離心力的作用增大導致核心受到擠壓偏心嚴重，最終導致水膜失穩。

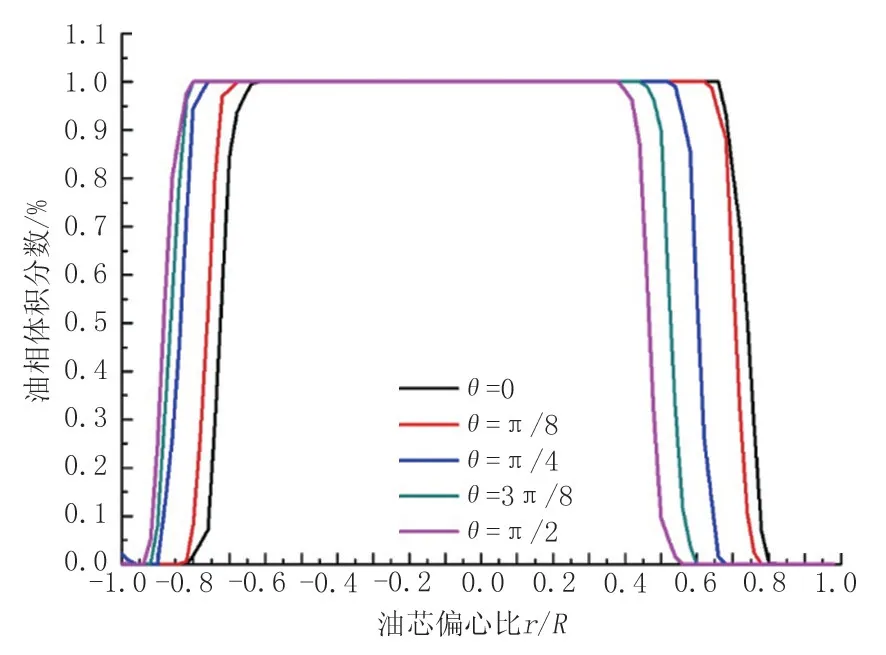
圖8 入口流速為0.9 m/s時彎管中各截面的油相體積分數分布Fig.8 Oil phase volume fraction distribution of each section in the elbow with the inlet flow rate of 0.9 m/s

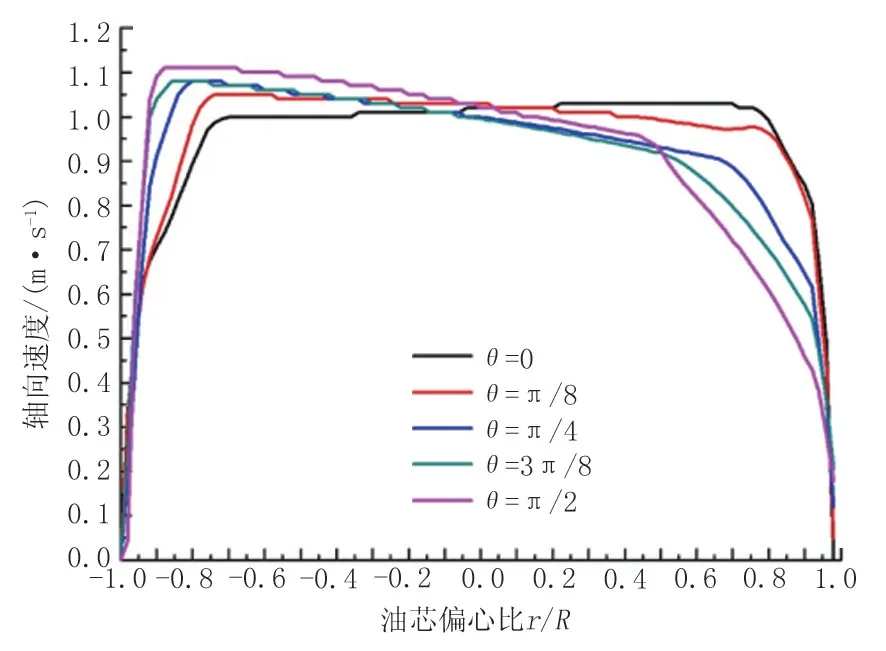
圖9 流速為0.9 m/s時水環在彎管不同位置處的軸向速度分布Fig.9 Axial velocity profile of water ring at different locations of elbow with the flow rate of 0.9 m/s

3.1.3 界面壓力分布

入口流速為0.9 m/s 時彎管不同截面的壓力分布如圖10 所示。從圖10 可以看出，彎管截面壓力分布呈現為水層區彎管外側壓力高、內側壓力低，油芯壓力高于水層壓力。

3.2 密度對彎管水環的影響

圖11 為入口流速為0.3 m/s、表面張力為0.15 N/m時，不同油品密度下水環在彎管內部的油水體積分數云圖，圖12 為彎管在不同油品密度下、不同界面位置處的油水體積分布相圖。

從圖中可以看出，彎管內部核心油流的偏移程度隨著油水密度比的減小而增大。油的密度越小，核心油流越向上偏移，當油品的密度為700 kg/m3時，經過彎管所帶來的離心力已經不是導致水膜失穩的主要因素。原因是隨著油品密度的降低，彎管離心力減小，油芯在離心力作用下向管壁外側偏移程度減小，而此時水油密度差較大，導致核心油流在水膜中所受的浮力增大，油芯上浮靠近上壁面。雖然此時彎管內部油芯同時受到浮力和離心力作用，但此時浮力占主導因素。

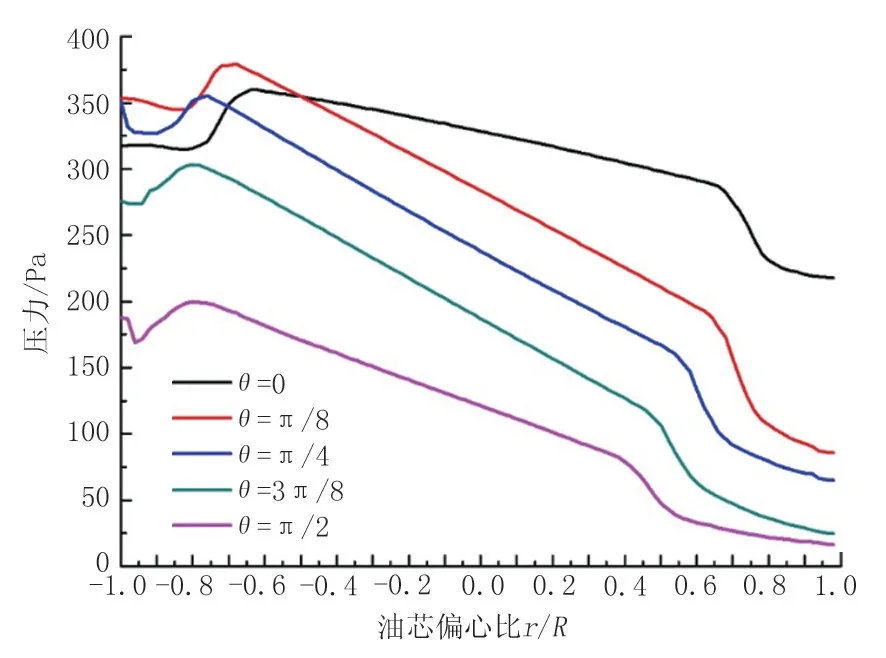
圖10 入口流速為0.9 m/s時彎管不同截面處的壓力分布Fig.10 Pressure distribution at different sections of elbow with the inlet flow rate of 0.9 m/s

圖11 不同油品密度下水環在管道中的油水體積分數切向分布Fig.11 Tangential distribution of the oil and water volume fraction in the pipeline with different oil density

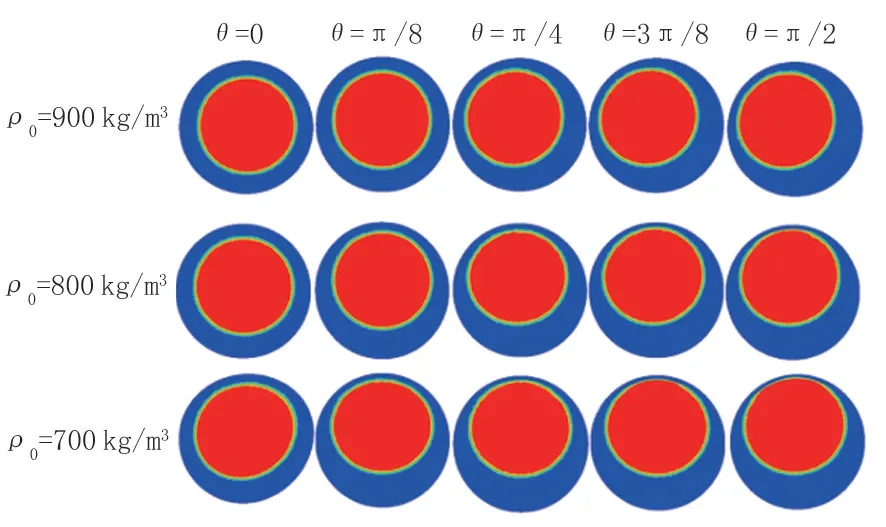
圖12 不同油品密度下水環在管道內的5個橫截面位置處油水體積分數分布Fig.12 Oil and water colume fraction distribution of five section in the pipeline with diferent oil density

3.2.1 界面油水體積分數分布

圖13 為油相密度為700 kg/m3時彎管不同截面處的油相體積分數分布曲線，從圖中可以看出，當θ=0時，油芯主要聚集在管道的中心，具有輕微的向上偏移的趨勢，隨著彎管角度的增大，水環向上偏心的幅度增大。在浮力的作用下，油相逐漸上浮靠近上側管壁。

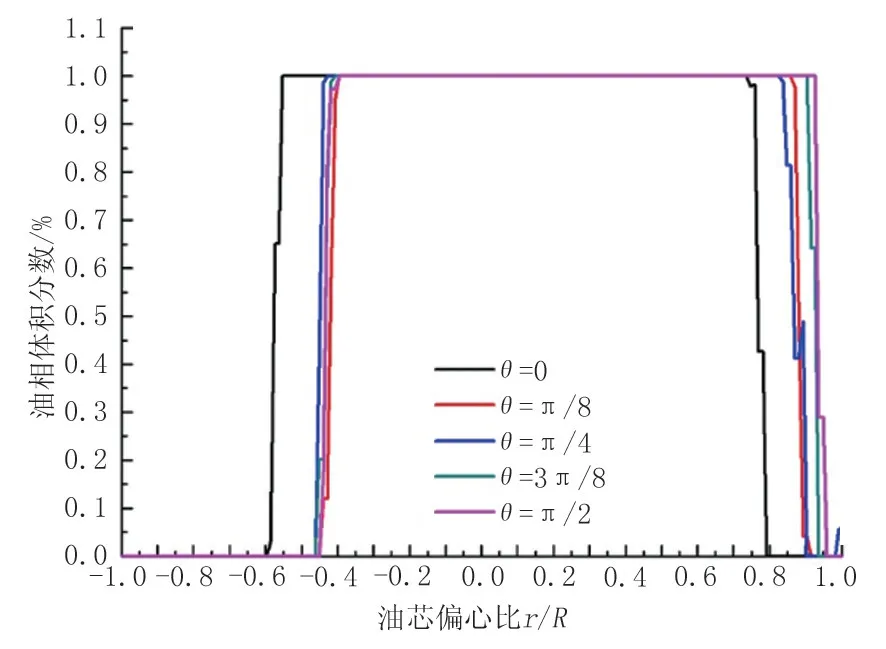
圖13 油相密度為700 kg/m3時彎管中各截面的油相體積分數分布Fig.13 Oil phase volume fraction distribution of each section in elbow with oil phase density of 700 kg/m3

3.2.2 界面速度分布

油水密度比為0.7 時彎管不同截面的軸向速度分布如圖14 所示，在此條件下軸向速度基本不隨彎管截面角度變化而變化。當θ=0 時，在油芯偏流比-1～-0.5 區域，中心環狀流流速逐漸由0 增加到0.38 m/s；在油芯偏流經-0.5～0.75 的區域，中心環狀流流速基本持平，保持在0.38 m/s。在油芯偏流比0.75～1 區域，速度由0.38 m/s 驟降到0。這說明，核心油流區流速基本保持不變，水層區速度梯度很大，剪切主要發生在水層區。且在油芯偏流比0.75～1區域剪切最強烈，剪切區厚度較小，這說明彎管上側的水膜在浮力的作用下受到核心油流的擠壓而變形，管道上側水膜厚度變小，管道下側的水膜厚度變大。

圖14 油水密度比為0.7時水環在彎管不同位置處的軸向速度分布Fig.14 Axial velocity distribution of water ring at different locations of elbow with the oil-water density ration of 0.7

3.2.3 界面壓力分布

油水密度比為0.7 時，彎管不同截面的壓力分布如圖15 所示。從圖中可以看出，彎管截面壓力分布呈現為水層區彎管外側壓力高、內側壓力低，油芯壓力高、水層壓力低。

圖15 油水密度比為0.7時彎管不同截面處的壓力分布Fig.15 Pressure distribution at different sections of elbow with the oil-water density ratio of 0.7

3.3 黏度對彎管水環的影響

當入口流速為0.3 m/s 且表面張力為0.2 N/m、油品密度為900 kg/m3時，水相黏度保持0.001 Pa·s不變，通過改變油品黏度改變兩相黏度比，水環在不同黏度比下的油水體積分數如圖16 和圖17 所示。當黏度比為200∶1 時彎管外側的水膜在離心力的作用下受到核心油流的擠壓而變形，同時彎管上側的水膜在浮力的作用下受到核心油流的擠壓而變形，管道上側水膜厚度變小，管道下側的水膜厚度變大。黏度比增大或減小，水膜在管道中的油水體積分布基本無變化，油品黏度在一定范圍內對水膜的穩定性未產生明顯影響。

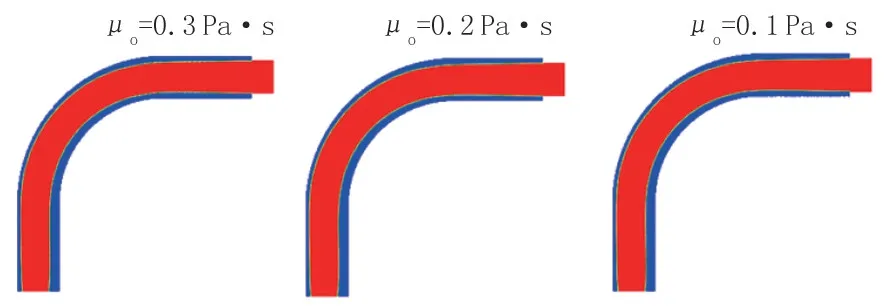
圖16 不同黏度比下水環在管道中的油水體積分數切向分布Fig.16 Oil and water volume fraction tangential distribution in the pipeline with different viscosity

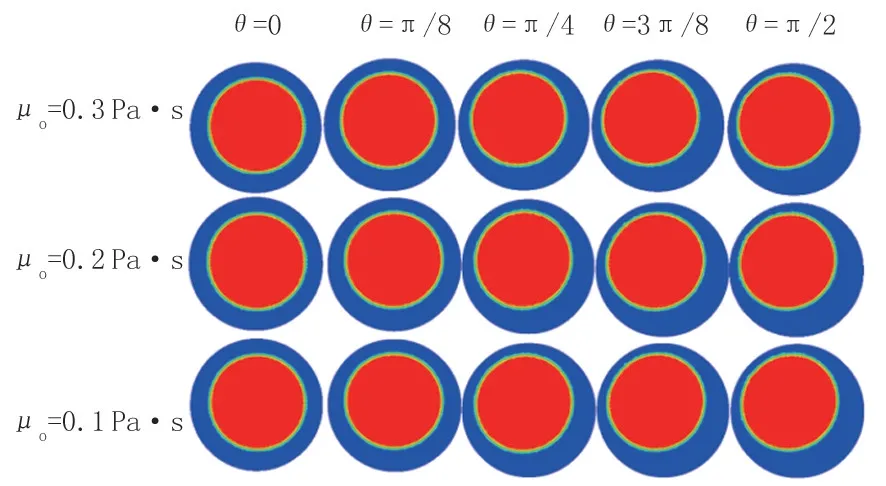
圖17 不同黏度比下水環在管道5個模型橫截面位置處油水體積分數分布Fig.17 Oil and water volume fraction distribution of water ring at five model section locations of pipeline with defferent viscosity

4 結論

借助FLUENT 軟件研究了不同工況下水環在90°彎管中的流動情況，得出以下結論：

（1）流速過大時，由于離心力的作用增大，核心油流向彎管外側偏移嚴重，在討論條件下當流速為0.3 m/s時，水環的穩定性最好。

（2）油水密度比較小時，由于浮力作用增大，核心油流向彎管上側偏心嚴重，在討論條件下當油水密度比為0.9時，水環的穩定性最好。

（3）油品的黏度對彎管中水環的穩定性影響較小，在一定范圍內，油品黏度增大或減小，水環在管道中的油水體積分布基本不變。