基于最優預瞄的智能車變道控制

邱少林 錢立軍 陸建輝

合肥工業大學汽車與交通工程學院，合肥,230009

0 引言

智能車主動變道主要涉及變道決策機制、變道軌跡規劃和變道軌跡跟蹤三方面的關鍵技術。在智能車自主變道軌跡跟蹤方面，人們期望在未來的控制研究中能夠充分利用優秀駕駛員的駕駛控制方法和習慣[9]。文獻[10]提出了一種基于改進的預瞄跟隨駕駛員模型的電動汽車智能轉向控制策略。針對自動駕駛車輛的大曲率轉向控制問題，文獻[11]研究了擬人轉向控制模型，并設計了并聯的模糊控制器；文獻[12]提出了一種動態雙點預瞄策略，設計了橫縱向模糊控制器。但上述文獻中的模糊規則難以建立，高控制精度條件下控制器的實時性難以保證。

為充分考慮智能車變道過程中道路的動力學特性, 本文建立了車輛二自由度簡化模型及道路模型；基于“預瞄-跟隨”理論建立了智能車自主變道過程中多點最優預瞄軌跡跟蹤控制模型，并利用線性二次型調節器(linear quadratic regulator,LQR)理論設計了軌跡跟蹤控制器，以實現智能車變道過程中的轉向控制；在MATLAB/Simulink中建立了自主變道的決策模塊、參考軌跡模塊及軌跡跟蹤控制模塊，在CarSim中建立了駕駛場景與傳感器模型，并設置了仿真工況，從而實現了基于MATLAB/Simulink和CarSim的智能車自主變道的聯合仿真，且結合實車測試結果驗證了所設計控制器的控制效果。

1 車輛動力學建模

構建一個精確且能夠反映車輛運動學與動力學特性的模型是進行智能車變道軌跡跟蹤控制的前提。由于車輛是一個非常復雜的非線性時變系統，建立一個可完整地反映各方面特性的動力學模型既不現實也沒有必要。為使汽車橫向換道模型計算不至于過于復雜，將汽車簡化為二自由度模型進行研究[13]。在分析的過程中作了如下的假設：①忽略懸架的影響，認為汽車的運動在一個平面上；②汽車縱向速度恒定；③汽車只有沿y軸的橫向運動和繞z軸的橫擺運動兩個自由度。

在進行智能車變道軌跡跟蹤的控制中，實際上是通過控制轉向盤實現對車輛行駛軌跡的控制。所以，考慮車輛橫向與橫擺運動兩個自由度的車輛動力學模型就可滿足要求，如圖1所示。

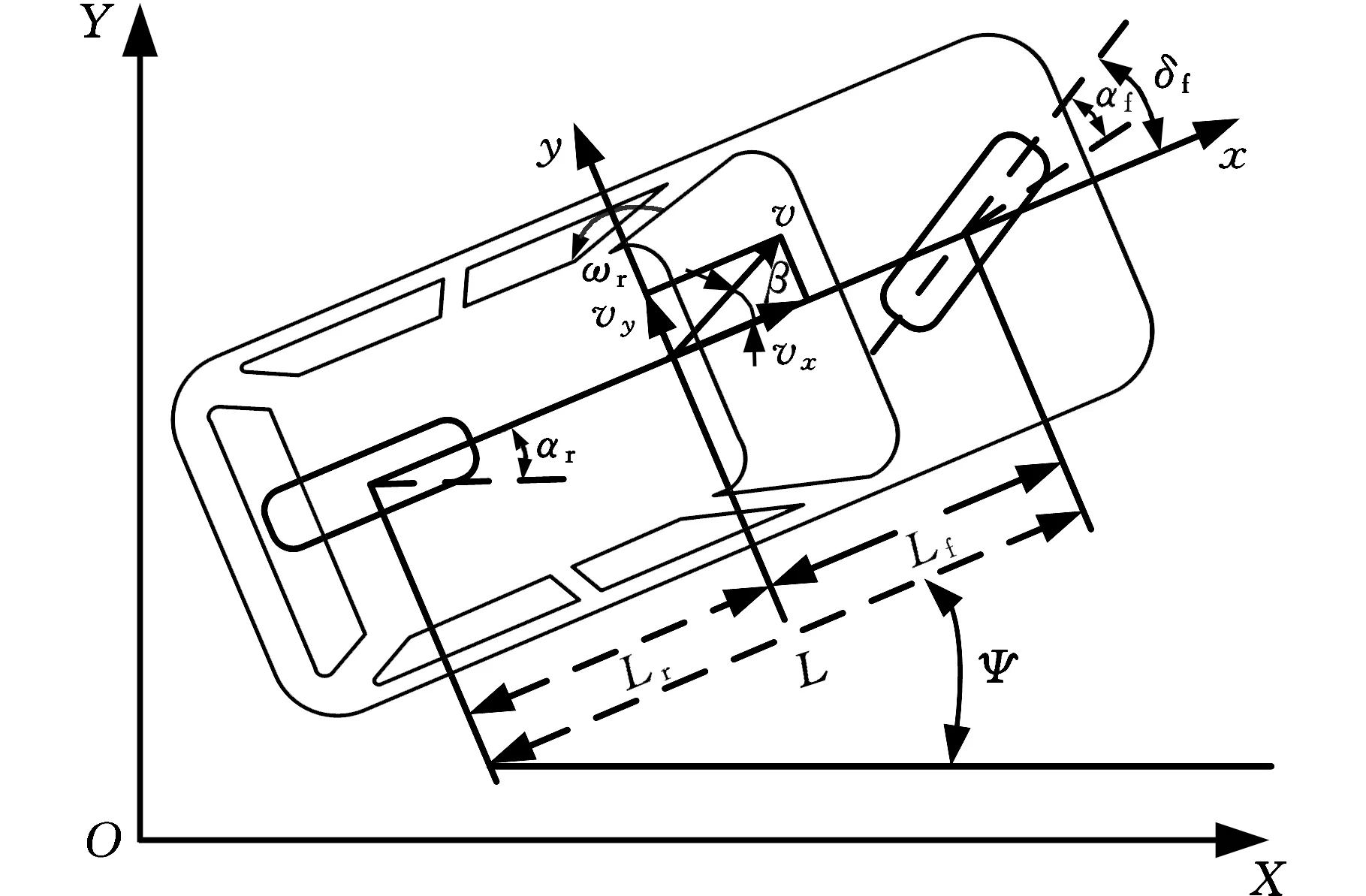
圖1 車輛動力學模型Fig.1 Vehicle dynamics model

二自由度車輛模型狀態空間方程為

(1)

式中，MCG為整車質量；vx為汽車縱向行駛速度；vy為汽車的橫向速度；β為汽車質心側偏角；ωr為汽車橫擺角速度；δf為汽車前輪轉角；L為軸距；Lf為質心到前軸的距離；Lr為質心到后軸的距離；Iz為車輛繞z軸橫擺轉動慣量；Cf、Cr分別為前后輪胎的側偏剛度。

式(1)表示的車輛模型狀態空間方程是以車輛坐標系為參考坐標系建立的,而在變道軌跡跟蹤過程中，期望的路徑是以大地坐標系為參考的，所以為得到車輛位置在大地坐標系下的坐標(圖1)，應對其坐標系進行轉換：

(2)

(3)

式中，X、Y為大地坐標系下車輛的位置坐標；Ψ為大地坐標系下車輛的實際航向角。

綜上，可得到以轉向盤轉角θ為輸入，以車輛橫向速度vy、橫擺角速度ωr、橫向位移y和航向角Ψ為狀態變量的狀態空間方程：

(4)

式中，n為轉向盤到車輪的傳動比。

將狀態空間方程(式(4))寫成標準形式，并離散后得到：

x(k+1)=Adx(k)+Bdθ(k)

(5)

x(k)=[vy(k)ωr(k)y(k)Ψ(k)]

式中，x(k)為狀態變量；θ(k)為控制變量；Ad為系統矩陣；Bd為控制矩陣。

2 軌跡跟蹤控制器設計

2.1 “預瞄-跟隨”理論

“預瞄-跟隨”理論描述了系統中參考未來輸入信息而進行的控制方法，從系統構成而言可理解為預瞄器和跟隨器兩者串聯組成的系統。最優預瞄的理論依據是駕駛員開車過程中，通過對道路前方信息進行預估，使得車輛實際軌跡與理論軌跡的偏差最小，從而得到一個最優的轉向盤轉角輸入[14-16]。

2.2 道路預瞄模型

在建立道路預瞄模型時，通過采樣將連續的道路中心線轉換為離散形式。其具體的轉換過程類似于“隊列”：選擇N個離散點，并將其作為系統的狀態變量。新的離散點繼續進入系統，先進先出，然后重復上述方式，直到所有道路采樣點逐漸進入系統[17]。隨著時間的推移，這些離散點將逐漸靠近車輛，如圖2所示。

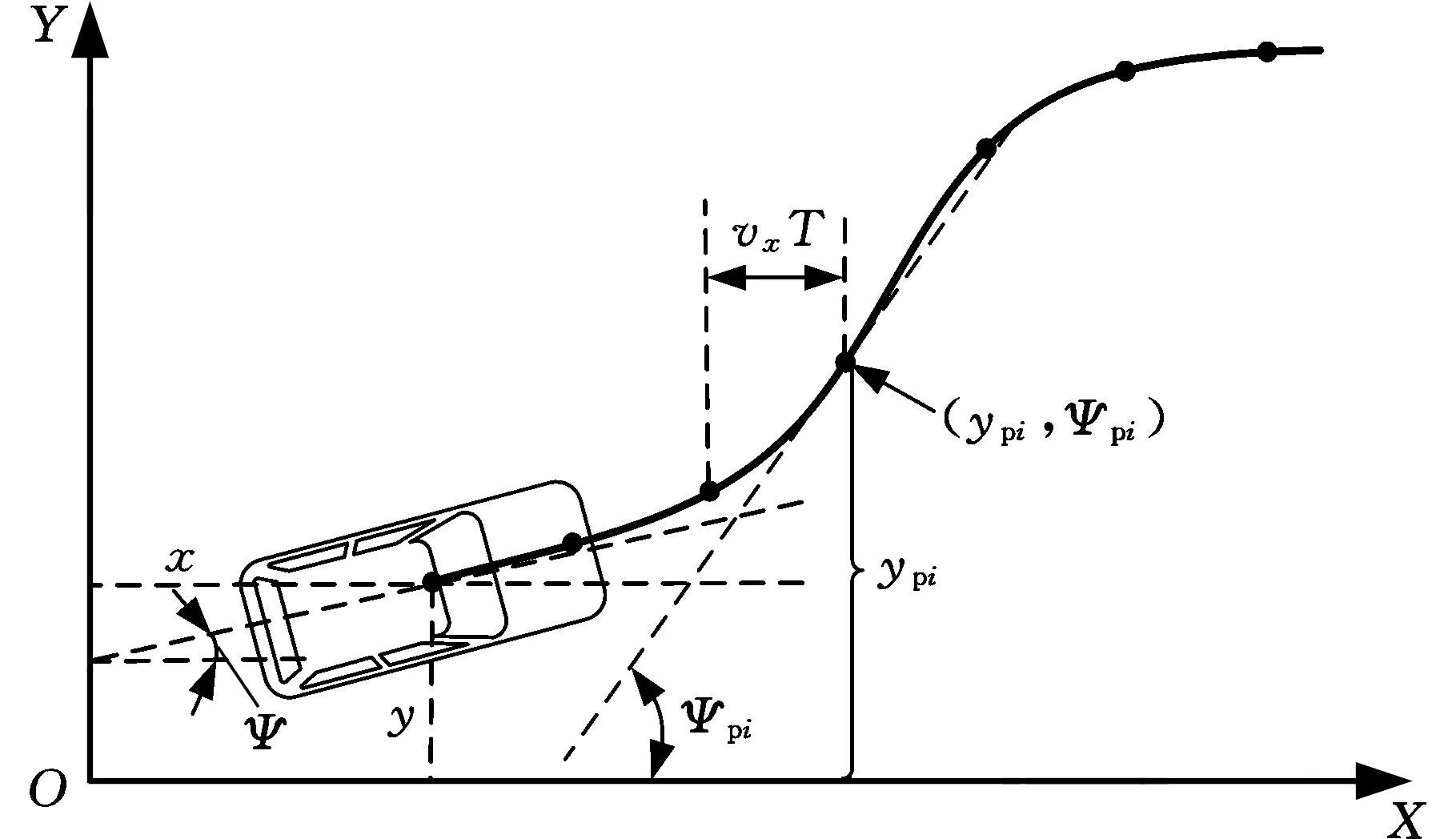
圖2 大地坐標系下的道路預瞄模型Fig.2 Road preview model in geodetic coordinate system

圖2中，T為時間步長，ypi為大地坐標系下道路點i的橫向位置，Ψpi為大地坐標系下道路點i上的期望航向角。假設前面的道路被分成N個等距點(即共有N個道路點)，則道路預瞄模型可表示為

y(k+1)=Dy(k)+Eyp(k)

(6)

yp(k)=[yp1(k)yp2(k) …ypN(k)]T

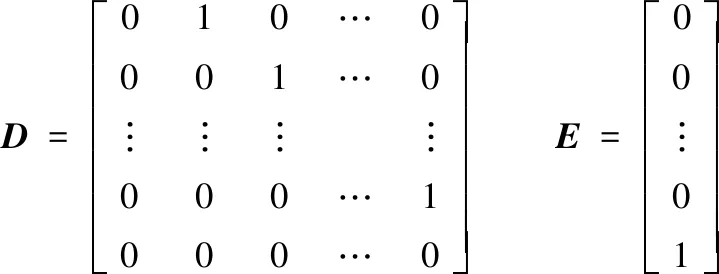
式中，yp(k)表示道路輸入；D、E為道路預瞄模型的系統矩陣。

在實際情況下，駕駛員在決策時使用的信息是基于車輛坐標系觀察到的，如圖3所示，其中Ψri為車輛坐標系下道路點i上的期望航向角。駕駛員獲得的道路信息是車輛坐標系下的觀測值yri(k)(即駕駛員使用車輛與預瞄道路之間的相對誤差)，而不是大地坐標系中的觀測值ypi(k)。

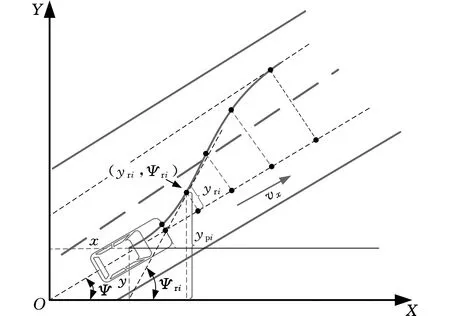
圖3 車輛坐標系下的道路預瞄模型Fig.3 Road preview model in vehicle coordinate system

假定航向角非常小，在大地坐標系中，車輛橫向位移可定義為

ypi(k)=y(k)+yri(k)+ivxTΨ(k)

(7)

2.3 控制器設計

本文基于上述“預瞄-跟隨”理論和“車輛-道路”模型，提出了最優預瞄軌跡跟蹤控制模型。基于LQR理論，充分考慮道路信息，設計了軌跡跟蹤控制器，可將車輛與道路整合為一體[18]。圖3顯示了“道路-車輛”系統，其狀態空間方程如下：

(8)

構造的代價函數可表示為

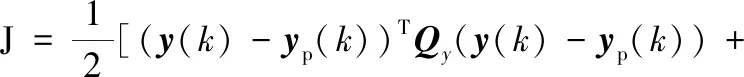
(9)

Ψe(k)=Ψri(k)-Ψ(k)

式中，Qy、QΨ和Qθ分別為橫向位移偏差、航向角偏差和轉向盤轉角輸入誤差的權重矩陣。

當代價函數J達到最小值時，可獲得狀態反饋增益矩陣：

KG=[kxkp]

(10)

其中，kx=[k1k2k3k4]為與車輛狀態變量x(k)=[vy(k)ωr(k)y(k)Ψ(k)]相關的狀態增益矩陣，kp=[kp1kp2…kpN]為與道路信息相關的預瞄增益矩陣。從而可得到最優的轉向盤轉角控制輸入：

(11)

其中，大地坐標系下最優轉向盤轉角可表示為

(12)

車輛坐標系下的最優轉向盤轉角可表示為

(13)

由式(12)和式(13)可得

3 仿真分析

3.1 仿真模型的建立

為驗證所設計控制器的有效性，本文采用聯合仿真對所構建的控制模型進行仿真驗證。CarSim仿真軟件可方便靈活地定義試驗環境和試驗過程，詳細地定義整車各系統的性能參數與特性文件，且CarSim與MATLAB/Simulink可實現無縫連接。目前，CarSim軟件已在國內外各大汽車制造廠和零部件公司得到了廣泛的應用，并已成為汽車行業的標準軟件。

本文的仿真過程主要涉及如下5個步驟：

(1)交通環境仿真建模。建立智能車及交通參與車輛的模型，其中智能車模型的參數見表1；單車道寬度為3.5 m的五車道道路示意圖見圖4。

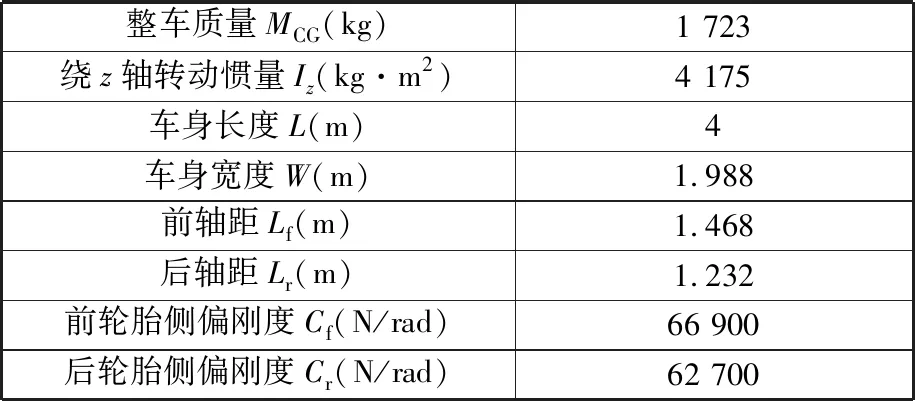
表1 整車參數Tab.1 Vehicle parameters

圖4 仿真環境模型Fig.4 Simulation environment model

(2)傳感器仿真建模。該模型包括1個前向測距雷達傳感器和4個角雷達測距傳感器。

(3)控制系統仿真建模。基于MATLAB/Simulink軟件建立控制系統仿真模型，包括變道決策模塊、變道參考軌跡模塊和軌跡跟蹤控制模塊，如圖5所示。

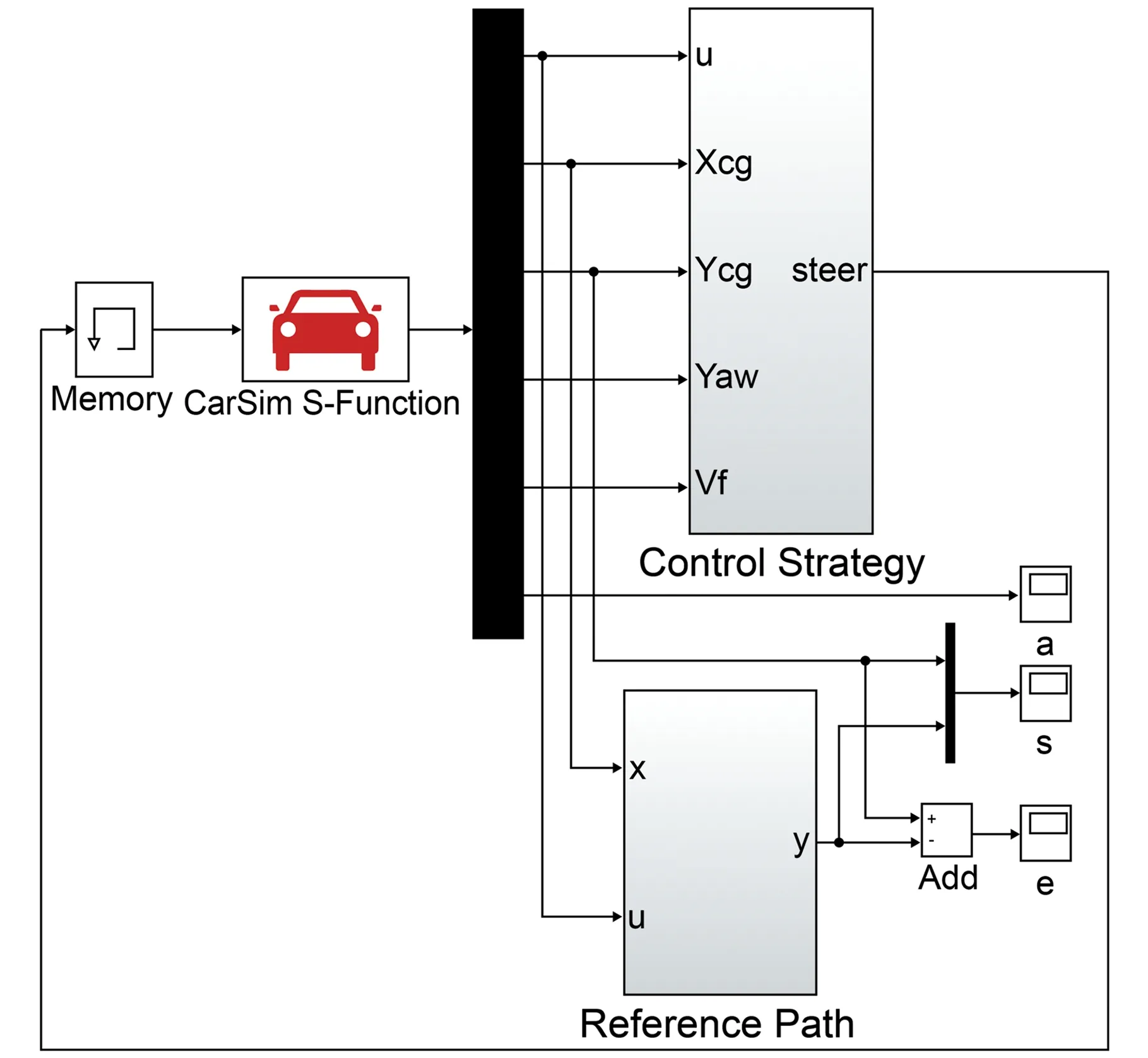
圖5 控制系統仿真模型Fig.5 Control system simulation model

(4)運行仿真工況。仿真工況的參數包括智能車與交通參與車輛的行駛狀態參數、仿真時間等。

(5)仿真結果后處理。依據仿真結果生成仿真動畫與曲線。

3.2 變道軌跡的選取

建立智能車主動變道跟蹤控制過程中的仿真系統時，需選擇一條合適的實際車道變換軌跡作為智能車變道控制過程中的參考軌跡。本文采用基于sin函數的變道軌跡作為智能車換道的參考軌跡，其數學表達式如下：

(14)

式中，S為變道結束時的橫向距離；d為變道結束時的縱向距離。

3.3 仿真結果分析

在MATLAB/Simulink環境中，將上述所建立的智能車變道控制過程中的系統模型與CarSim和MATLAB/Simulink連接時生成的S-Function模塊相連接，以完成仿真模型的建立。在本研究過程中，假設智能車是勻速行駛的，分別設置智能車在30 km/h、50 km/h和70 km/h的速度下勻速行駛，設定變道橫向距離為3.5 m，并對控制模型的性能進行了仿真驗證。將仿真得到的變道行駛軌跡與依據式(14)得到的參考變道行駛軌跡進行了對比，上述3種速度下的變道軌跡見圖6，橫向偏差見圖7，橫擺角速度見圖8。

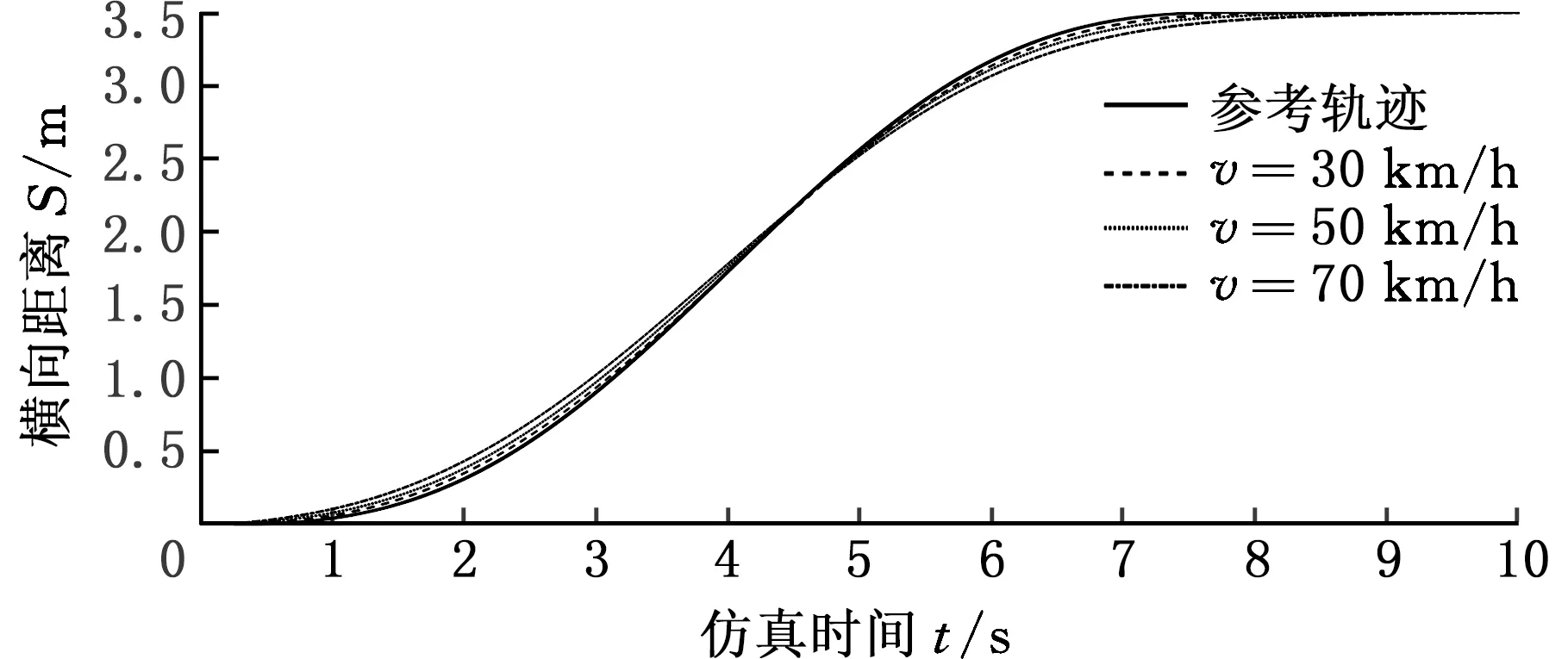
圖6 變道軌跡Fig.6 Lane-change trajectory

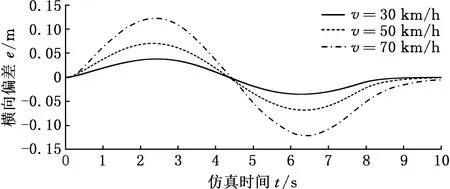
圖7 橫向偏差Fig.7 Lateral deviation

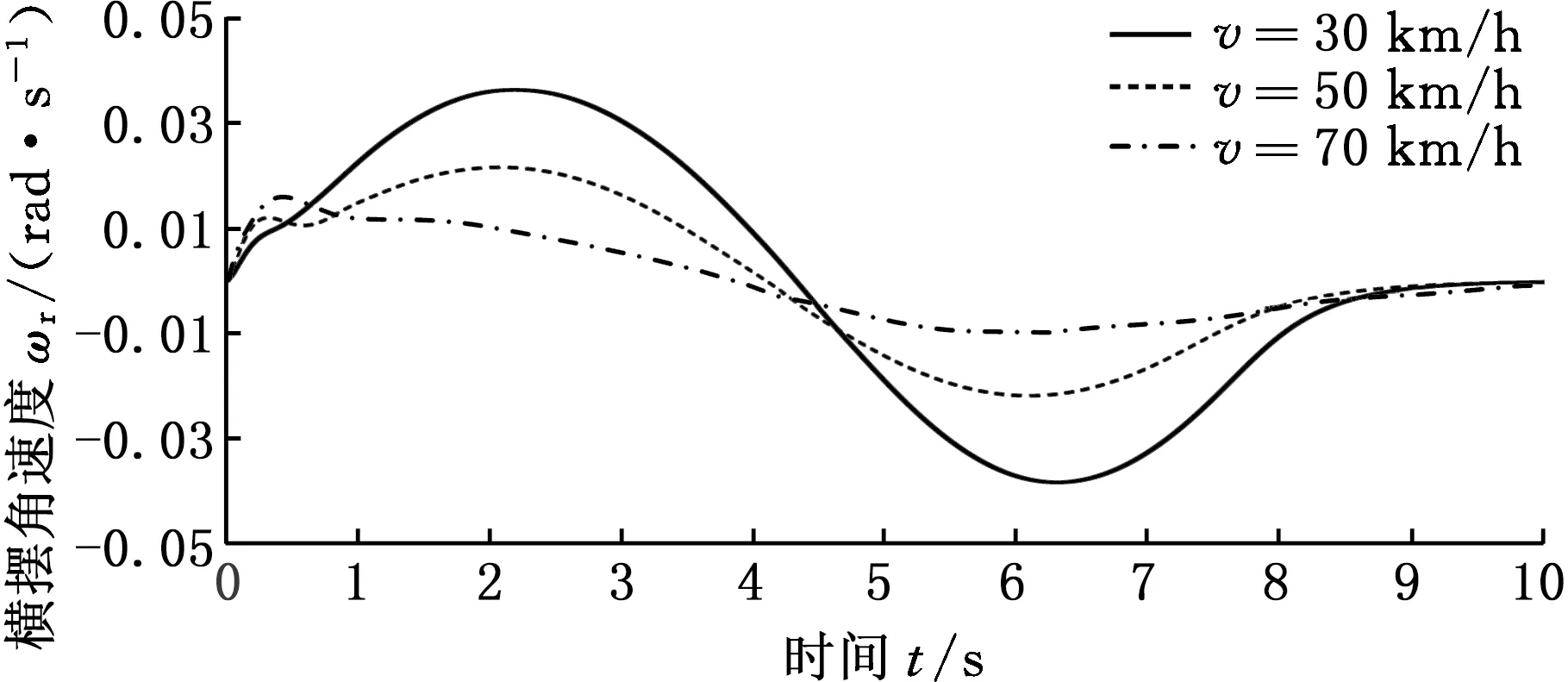
圖8 橫擺角速度Fig.8 Yaw rate

由圖6和圖7可以看出，智能車變道過程中，仿真得到的變道行駛軌跡與參考變道行駛軌跡的偏差呈先變大、再變小、再變大、再變小的變化趨勢；當智能車車速為30 km/h時，仿真得到的變道軌跡與參考變道軌跡基本重合，可很好地跟蹤參考軌跡行駛；當智能車車速為70 km/h時，仿真得到的變道軌跡與參考變道軌跡在變道過程中的偏差變大，兩者變道軌跡的最大偏差為0.15 m；變道過程中，隨著速度的增大和仿真過程的進行，變道縱向距離也在增大，控制模型隨著速度的變化而進行了調整，具備很好的魯棒性。

由圖8可以看出，仿真過程中智能車的最大橫擺角速度約為0.04 rad/s。根據文獻[19]可計算出本研究設置的3種速度下車輛期望橫擺角速度的最小約束值約為0.4 rad/s，所以本研究中3種工況下智能車的橫擺角速度均滿足條件，在變道過程中車輛具備良好的穩定性。

4 實車測試

為更好地驗證所設計控制器的控制效果，本文將所設計的控制器部署到樣車上并進行實車測試，測試系統如圖9所示。試驗過程中撥動轉向燈操縱桿來觸發變道指令。試驗具體過程如下：①采集試驗環境下的基線位置信息;②測試車輛在車道線清晰且平坦的直道上分別以30 km/h、50 km/h和70 km/h的速度勻速行駛;③當目標車道無車時觸發變道，并采集變道時測試車輛的位置信息;④對每個速度值分別向左和向右變道測試5次;⑤對試驗數據進行處理，并得到測試車輛的變道軌跡。以30 km/h速度下向左變道的變道軌跡為例，其處理結果見圖10。

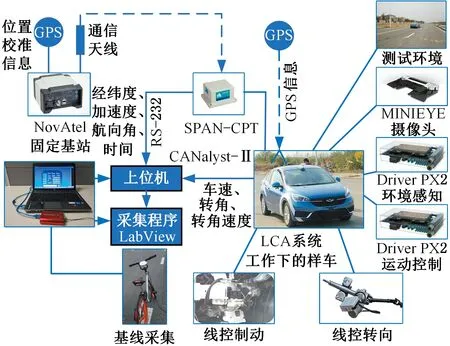
圖9 測試系統原理圖Fig.9 Schematic diagram of test system

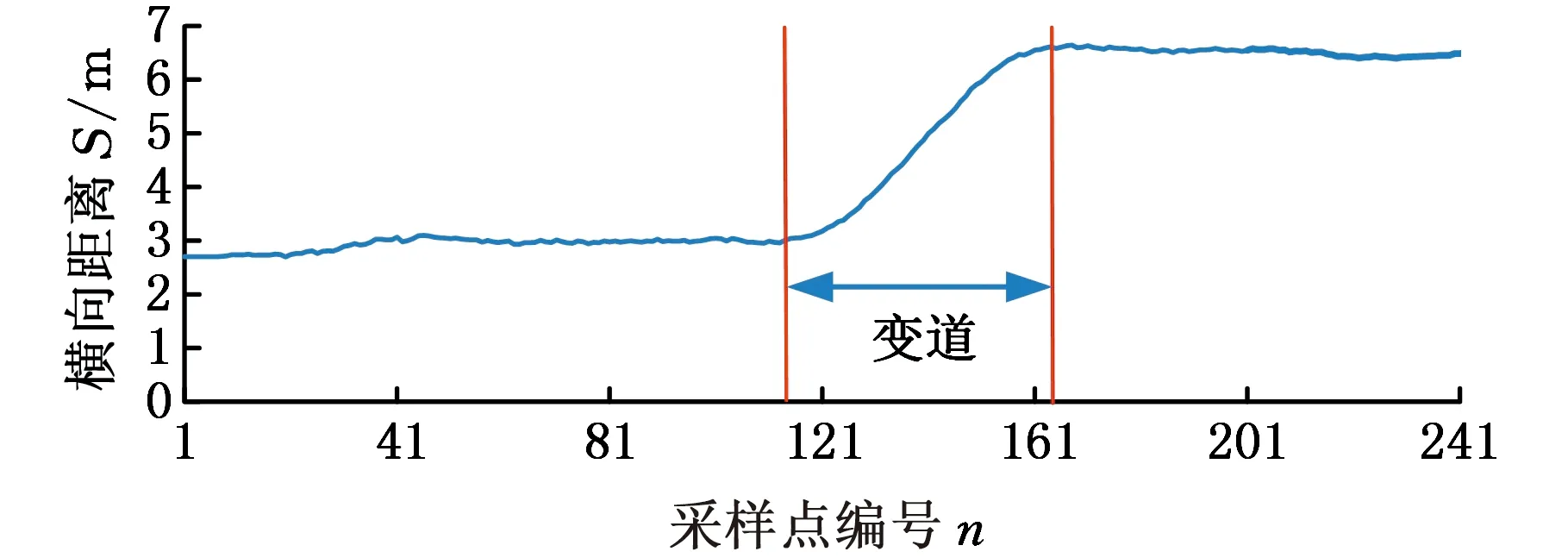
圖10 30 km/h向左變道Fig.10 Lane-change to left at 30 km/h

圖11為30 km/h、50 km/h和70 km/h速度下的仿真結果與實車測試結果的對比曲線。

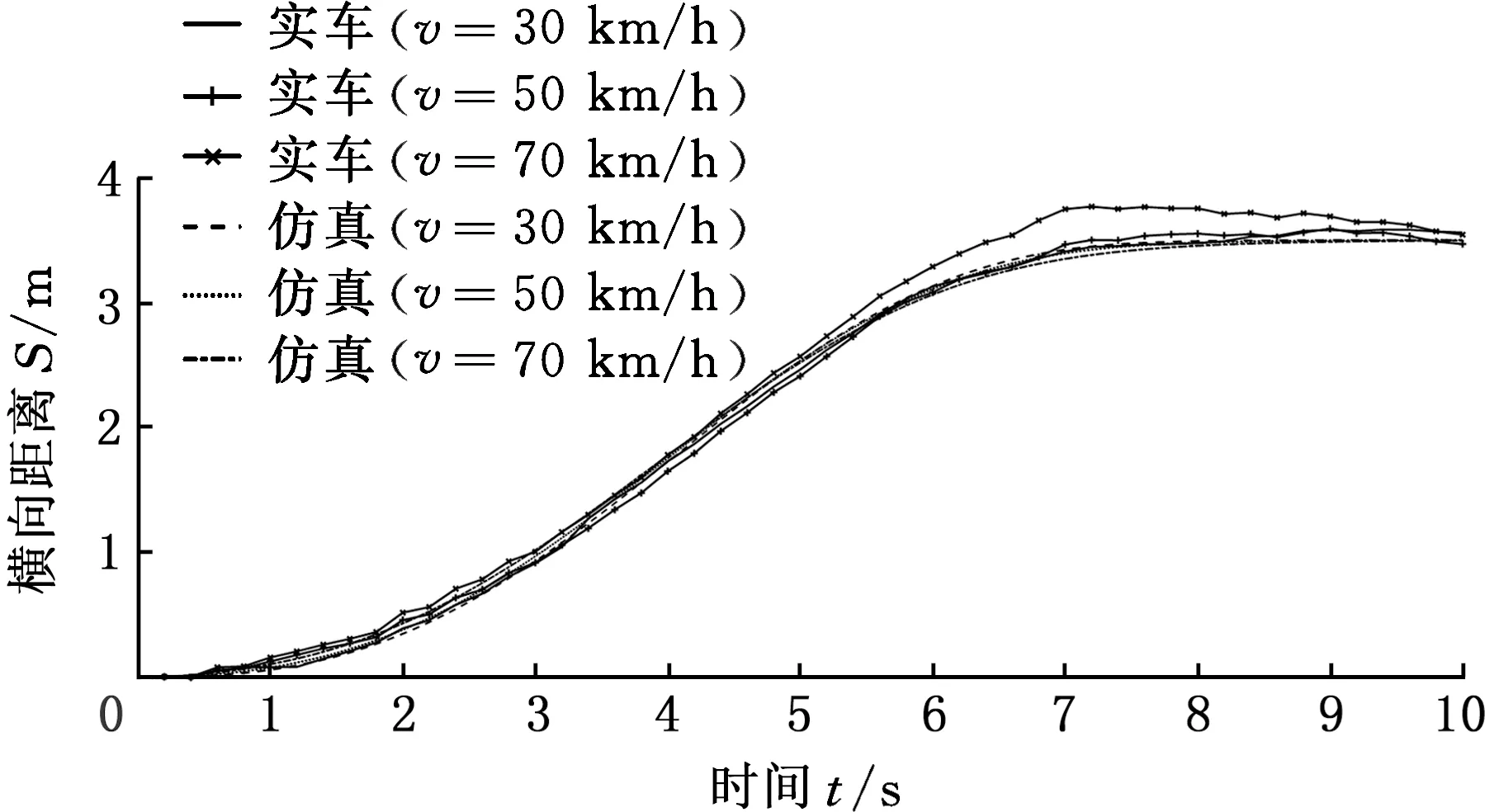
圖11 仿真與實車測試的對比Fig.11 Comparison of simulation and vehicle test

總體而言，雖然不同車速下的仿真結果存在一定差異性，但與實車變道測試相比較，本文所建立的仿真模型能夠正確控制智能車的橫向運動過程，仿真得到的橫向運動軌跡值與實測變道軌跡值較為接近，仿真曲線與實測曲線走勢相同，且總體比較接近，這表明本文所設計的智能車變道控制器具有較好的精確度。

5 結論

(1)基于“預瞄-跟隨”理論建立了智能車輛在變道過程中的最優預瞄軌跡跟蹤控制模型，并依據LQR理論設計了軌跡跟蹤控制器。

(2)在MATLAB/Simulink和CarSim的聯合仿真環境下，建立了智能車變道過程中的變道策略模塊、變道參考軌跡模塊和軌跡跟蹤控制模塊。分別對智能車在30 km/h、50 km/h、70 km/h勻速運行下的變道軌跡進行了虛擬仿真和實車測試，結果表明：虛擬仿真軌跡與實車變道軌跡的變化趨勢接近，且大部分的虛擬仿真軌跡與實際軌跡相重合，從而驗證了所設計的軌道跟蹤控制器具有較好的精確度，適用于智能車的自動變道控制功能。

(3)該控制模型的建立過程以實際車道變換軌跡為參考對象，并基于實車進行了相應工況下的測試驗證，因此基于該控制模型所設計的智能車自動變道控制器可體現駕駛員的真實駕駛行為，這將在很大程度上提高智能車的行駛穩定性。