智能車隊跟車縱向控制算法設(shè)計及仿真驗證

葉 心,魏勁鵬,楊杰星, 葉 明, 呂 強

(1.重慶理工大學 a.車輛工程學院；b.汽車零部件先進制造技術(shù)教育部重點實驗室，重慶 400054；2.重慶美萬新能源汽車科技有限公司，重慶 401121)

智能汽車是一個集外部環(huán)境感知、行駛路徑?jīng)Q策、車輛輔助控制等功能于一體的綜合系統(tǒng)，車輛的縱向控制技術(shù)是智能汽車最終“落地”的關(guān)鍵技術(shù)之一，目前已成為汽車領(lǐng)域研究的熱點及重點。將車輛縱向控制技術(shù)應用到智能車隊自動駕駛上，在緩解道路擁堵、保證交通安全以及駕駛節(jié)能等方面有重要意義[1]。

車輛縱向控制算法是連接上層跟車決策層和下層車輛執(zhí)行機構(gòu)的橋梁。上層控制器以車路相對位置為參照，規(guī)劃車輛的期望運動狀態(tài)，如駕駛?cè)四Ｐ蚚2-3]和人工勢場法[4-5]；下層控制器利用上層控制器的輸出設(shè)計車輛控制器，如LEE等[6]應用參數(shù)自整定模糊PID控制，通過模糊規(guī)則對PID的3個參數(shù)進行調(diào)節(jié)，實現(xiàn)汽車縱向控制。Hedrick等[7]提出三狀態(tài)模型，忽略發(fā)動機動態(tài)特性、液力變矩器特性、輪胎滑移，以進氣量、發(fā)動機轉(zhuǎn)速和制動力矩3個狀態(tài)進行車輛控制。部分學者采用直接式控制方式[8]和分層式控制方式[9-10]，建立并開發(fā)了參數(shù)自適應型速度控制策略,適用于強魯棒性控制系統(tǒng)，但未考慮車輛隊列行駛時的應用。在車輛隊列控制方面，張向南等[11-13]研究了車輛隊列縱向控制的基本理論、控制方法和實驗手段，未考慮領(lǐng)航車模型，但為車輛隊列系統(tǒng)控制提供理論基礎(chǔ)和技術(shù)支撐。

本文將車輛縱向動力學建模方法、模糊智能控制應用在車隊縱向跟車控制中，建立包括領(lǐng)航車模型、車隊縱向動力學模型、跟車模型等，為達到提高車隊通行效率以及安全行駛的目的，保證車隊車輛速度差小于5 km/h，車車間距差值波動率在靠近時小于20%，遠離時小于30%，最后通過仿真分析，驗證模型和控制器的性能和可行性。

1 領(lǐng)航車縱向動力學模型及仿真分析

領(lǐng)航車是車隊中位于首位的車輛，并按照給定的城市循環(huán)工況ECE中規(guī)定的車速、加速度以及減速度的指令行駛。本節(jié)首先建立領(lǐng)航車縱向動力學建模，包括駕駛員模型、發(fā)動機模型、變速器模型、換擋模型、制動系統(tǒng)模型以及整車驅(qū)動模型，這些模型在建立過程中進行了如下假設(shè)：

1) 假設(shè)在路況良好的平路上行駛，無坡度；

2) 汽車輪胎與地面有良好的接觸，并且地面有充足的附著力，不存在輪胎相對地面滑移之類的非線性因數(shù)；

3) 發(fā)動機的工作狀態(tài)為理想工作狀態(tài)下的瞬態(tài)修正。

與真實的道路情況相比，ECE只對道路車速、加減速、紅綠燈等因素進行了理想的模擬，考慮真實的道路存在打滑、彎道以及通訊延遲等實際情況，為了避免車輛隊列行駛時出現(xiàn)安全隱患，在車間距保持方面引入安全系數(shù)ζ。

1.1 研究對象

車隊中的車輛全部為國產(chǎn)某車廠的同一款前置前驅(qū)AMT轎車，其整車及動力系統(tǒng)參數(shù)如表1所示。

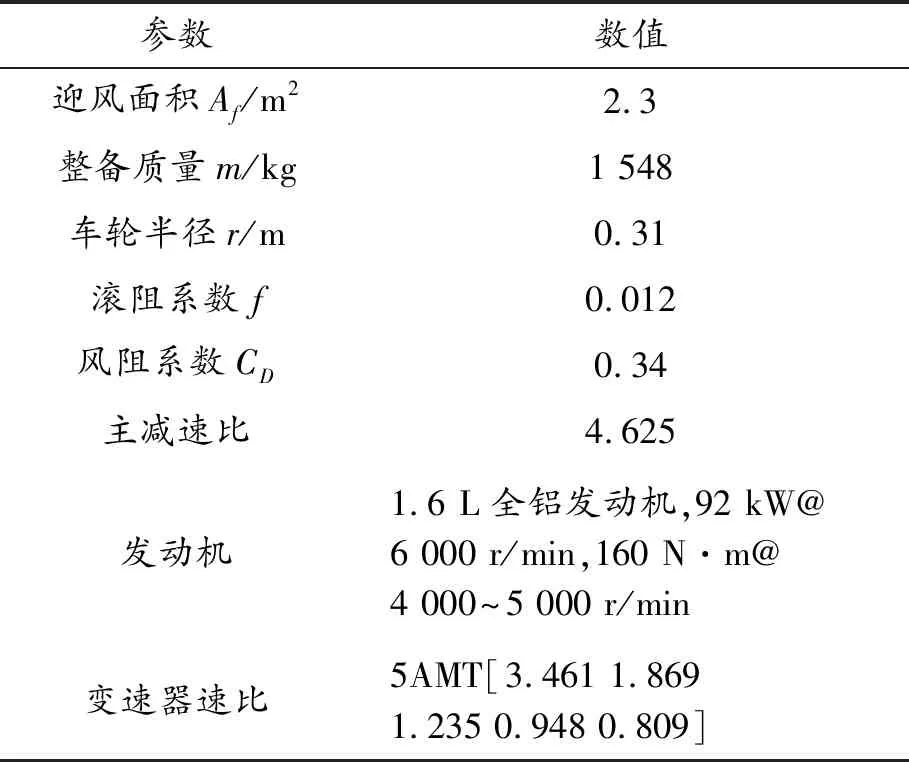
表1 整車及動力系統(tǒng)參數(shù)

1.2 領(lǐng)航車縱向動力學模型

領(lǐng)航車的縱向動力學模型，包括駕駛員模型、發(fā)動機模型、變速器模型、驅(qū)動橋模型(主減速器、差速器)以及制動系統(tǒng)模型5個部分，基于車輛動力學領(lǐng)域的研究成果以及經(jīng)驗數(shù)據(jù)，各個部分通過力矩、轉(zhuǎn)速的傳遞關(guān)系連接，建立單個車輛整車縱向動力學模型，如圖1所示。

1) 駕駛員模型

駕駛員模型提供整車模型的輸入信號，包括油門踏板開度以及制動踏板開度。為了使駕駛員模型接近真實的情況，采用具有強魯棒性的模糊邏輯智能算法，通過對比實際車速與期望車速的差值，以及該差值的變化率，將車速需求轉(zhuǎn)化為油門踏板或者制動踏板的開度，建立駕駛員模型，如圖2所示。

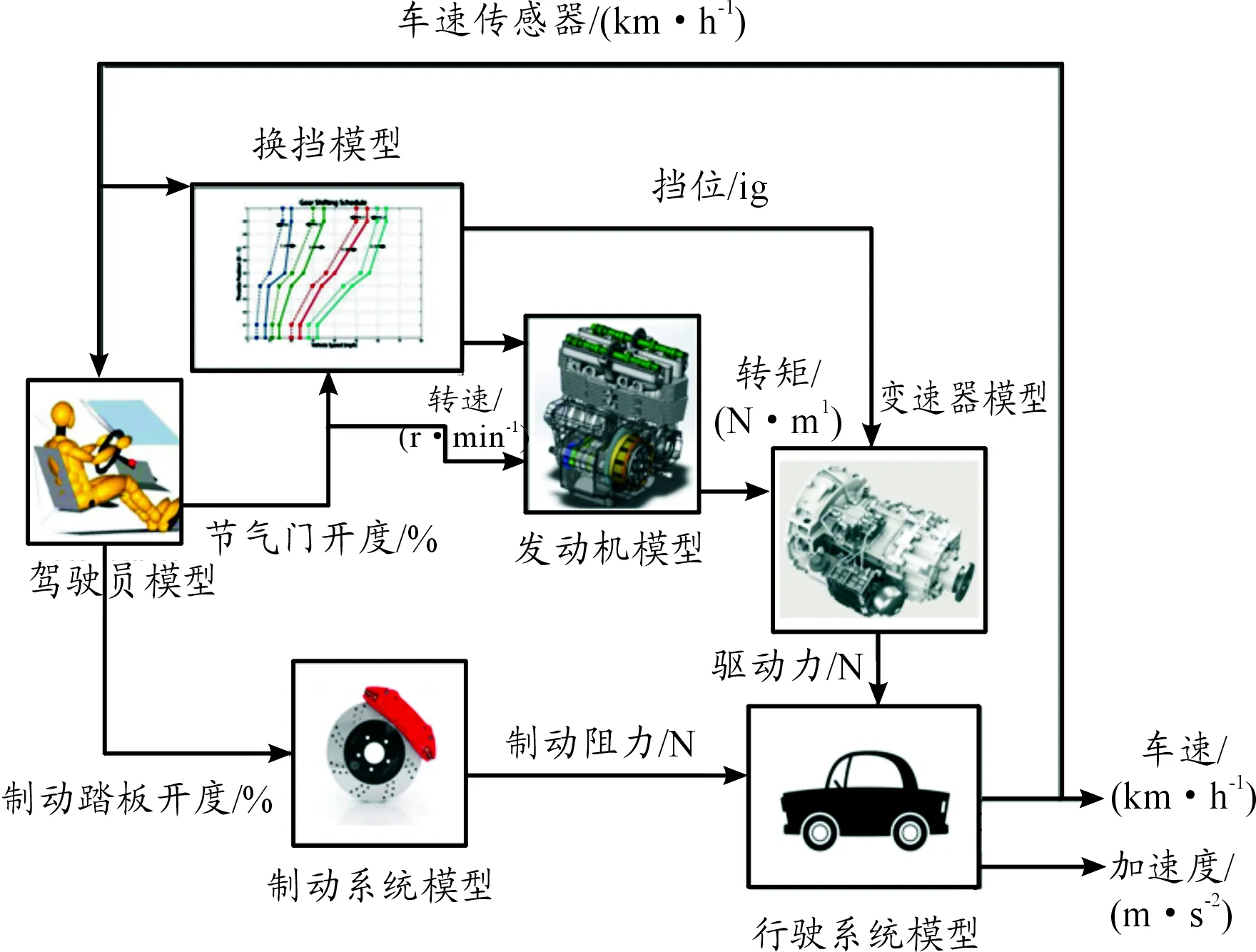
圖1 領(lǐng)航車縱向動力學系統(tǒng)模型

2) 發(fā)動機模型

由于發(fā)動機有動態(tài)工作負載，導致其常處于一種不穩(wěn)定的運行工況中。本文采用發(fā)動機穩(wěn)態(tài)數(shù)據(jù)擬合并動態(tài)修正的方法來建立發(fā)動機模型。根據(jù)內(nèi)燃機的工作原理可知，發(fā)動機所輸出的轉(zhuǎn)矩與曲軸的轉(zhuǎn)角、進入汽缸的混合氣體質(zhì)量、空燃比以及其他因素有關(guān)，在進行發(fā)動機系統(tǒng)動態(tài)建模過程中，基于發(fā)動機穩(wěn)態(tài)實驗數(shù)據(jù)，通過動態(tài)修正，搭建1階惰性發(fā)動機模型來補償動態(tài)誤差，如式(1)所示。

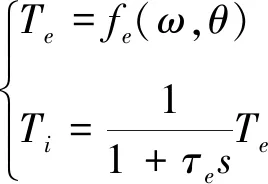
(1)

式中:Te為理想的發(fā)動機輸出轉(zhuǎn)矩(N·m)；θ為油門的開度；ω為發(fā)動曲軸轉(zhuǎn)速(r/min)；τe為發(fā)動機扭矩階躍響應時間常數(shù)；Ti為發(fā)動機實際輸出扭矩(N·m)。

3) 變速器模型

本文研究對象為5擋AMT自動變速器，可根據(jù)當前車速和節(jié)氣門開度選擇合適擋位。變速器輸入軸與發(fā)動機輸出軸通過離合器連接起來，起到減速增矩的作用，因此自動變速器的輸出軸扭矩Tg及轉(zhuǎn)速ng計算如式(2)所示。

(2)

式中ig為當前擋位傳動比。

基于式(2)及AMT綜合性換擋規(guī)律，在Matlab/Simulink/Stateflow仿真平臺搭建變速器換擋模型，如圖3所示。

圖2 領(lǐng)航車駕駛員模型

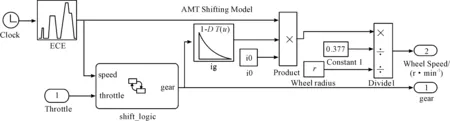
圖3 AMT換擋模型

4) 制動系統(tǒng)模型

制動系統(tǒng)模型是確保車輛按照預期的車速行駛，以及與前車保持安全距離的重要手段。駕駛員制動意圖可通過制動踏板力與期望制動減速度關(guān)系來表示，制動踏板力與期望制動減速度之間的關(guān)系如式(3)所示。

(3)

式中：Fb為估算出的制動踏板力(N);Pm、Am分別為人力制動主缸的壓力(Pa)及活塞有效面積(m2)；Ks為彈簧剛度(N·m-1);Rpedal為制動踏板杠桿比;Pb為制動踏板位移(m)，一般可以通過實車場地實驗的數(shù)據(jù)擬合等獲得。

5) 車輛行駛系統(tǒng)模型

假定車輛在良好路面行駛，且只考慮汽車的縱向受力情況，汽車行駛系統(tǒng)承受來自傳動系統(tǒng)輸出的轉(zhuǎn)矩轉(zhuǎn)化的驅(qū)動力Fx、空氣阻力Fw、滾動阻力Ff、加速阻力Fj以及制動阻力Fb，汽車受力平衡如圖4所示。

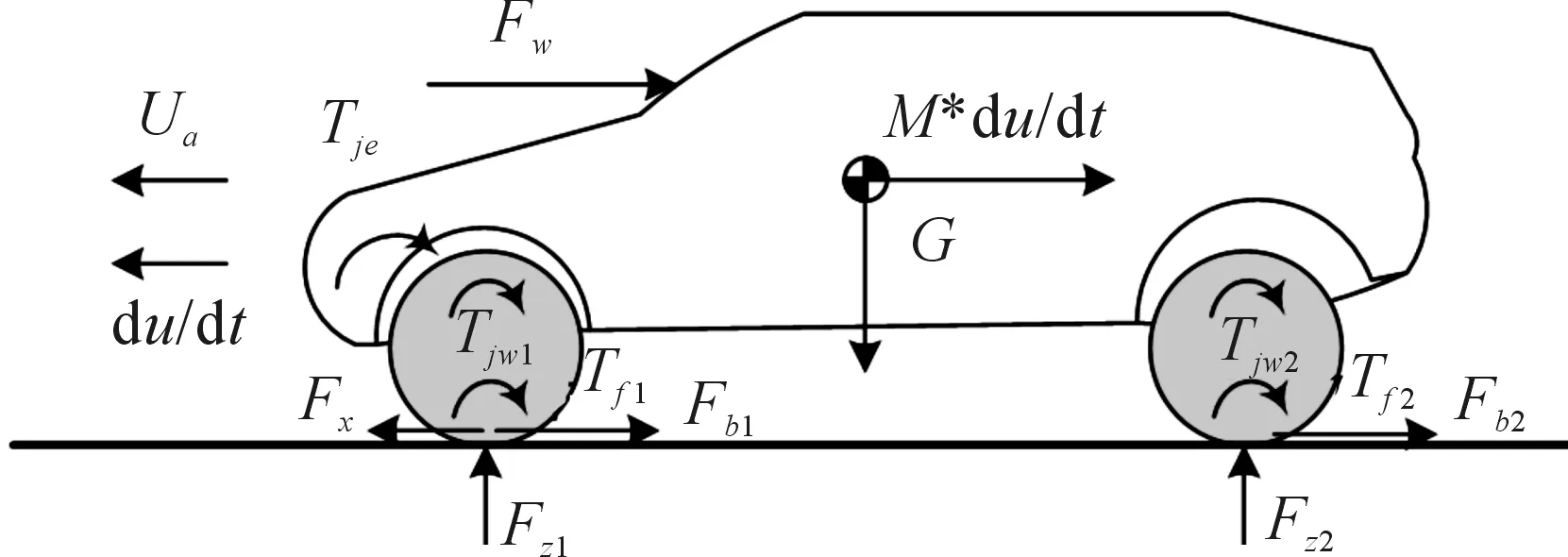
圖4 汽車受力平衡圖

根據(jù)圖4，得到汽車在行進過程中的受力平衡方程式：

Fx=Fw+Ff+Fb+Fj

(4)

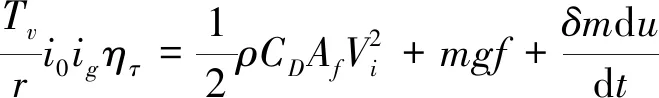
(5)

式中：δ為汽車的旋轉(zhuǎn)質(zhì)量轉(zhuǎn)換系數(shù)(根據(jù)經(jīng)驗數(shù)據(jù)δ>1，且在1.1～1.4之間，本文研究對象為C級轎車，故δ=1.3)；ρ為空氣密度(g/cm3)；CD為空氣阻力系數(shù)；Af為迎風面積(m2)；Vi為第i輛車的縱向速度(km/h)，忽略風速；Td為車輪處驅(qū)動轉(zhuǎn)矩(N·m)；Te為發(fā)動機飛輪處輸出轉(zhuǎn)矩(N·m)；m為汽車質(zhì)量(kg)；f為道路摩擦因數(shù)；du/dt為車輛縱向加速度(m/s2)；r為車輪半徑(m)；i0為主減速器傳動比；ig為變速器當前工作檔位速比；ητ為傳動系傳動效率。

1.3 領(lǐng)航車駕駛模型仿真分析

基于Matlab/Simulink/Stateflow仿真平臺，對上述小節(jié)中的領(lǐng)航車模型進行仿真分析，以ECE道路循環(huán)工況為目標車速，仿真結(jié)果如圖5所示。

圖5 領(lǐng)航車行駛車速與ECE車速對比

圖5中，虛線為ECE道路循環(huán)工況目標車速，實線為領(lǐng)航車的實際車速。通過仿真結(jié)果可知，領(lǐng)航車行駛車速與ECE循環(huán)工況的車速最大差值不超過2 km/h，較好地實現(xiàn)了領(lǐng)航車按照預定的車速，加速、減速行駛要求的目的。

2 智能車隊跟隨控制器設(shè)計及仿真分析

車輛的隊列行駛是指2輛以上的汽車，在以相同的車速行駛的基礎(chǔ)上，兩兩車輛之間按相近的車間距離保持有序行進的方式，可以確保交通安全，提高交通通行率。

傳統(tǒng)車隊間車距控制取決于駕駛員豐富的經(jīng)驗以及熟練的車輛控制技能，以確保車輛間的相對距離以及行駛的車速，而智能車車隊通過先進的傳感器(機器視覺、磁、雷達)來感知和獲取前方車輛的距離以及速度。本文根據(jù)該信號建立車隊跟隨控制器，確保車輛與車輛之間的安全距離，使其構(gòu)成一個不可分割的整體，如圖6所示。

假設(shè)車身長度均為L，Sdk為第k-1輛車與第k輛車之間的允許安全車距，Sdk+1為第k輛車與第k+1輛車之間的允許安全車距。ua和α為領(lǐng)航車車速和加速度，uak和αk為第k輛車的車速與加速度，uak+1和αk+1為第k+1輛車的車速和加速度。

圖6 車輛隊列行駛簡易模型圖

2.1 車間間距的控制策略

合理控制車車間距是車隊按一定通行率安全行駛的保障。目前，車距算法可分為固定間距算法和可變間距算法，后者又可分為固定車頭時距算法和可變車頭時距算法[14-15]。本文從安全角度出發(fā)采用可變車頭時距法，考慮以下幾種影響因素：① 所確定的車車間距必須考慮車隊當前車速、最大制動減速度等因素；② 兼顧車輛隊列行駛的穩(wěn)定性和交通的通暢性，密度合理，不會造成交通擁堵。

領(lǐng)航車按照給定的ECE城市工況為目標車速行駛，跟隨車輛則根據(jù)前車的車速以及車輛間的相對距離來控制本車的車速，使得前后車輛車速相近，為了保持車輛隊列行駛時的穩(wěn)定性，要求車車間距的波動率在遠離時不超過30%。由于汽車的縱向動力學模型存在很多的不確定性以及非線性因素，本文基于強魯棒性的智能模糊控制方法，建立車隊中各個車輛的跟隨控制算法，以實現(xiàn)車輛隊列行駛中車車間距的保持，詳見2.2節(jié)。

另外，車車間距控制策略中被控對象車距的確定對車隊穩(wěn)定性有重要影響，考慮到智能車隊車車之間有通訊，因此車車之間的安全距離與當前車速和加/減速度有關(guān)系，上述三者之間關(guān)系如式(6)所示。車速越大，安全距離越大；加速度越大，安全距離越大；減速度越大，安全距離越小。

Sdk=f(uak，αk)=tuak+ξdbk

(6)

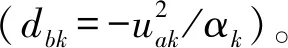
考慮到道路模型的復雜性，隊列中第k輛車與前車的實際距離可定義為：

di=Sdk+L

(7)

2.2 基于模糊智能控制的智能汽車跟隨模型

針對非線性控制系統(tǒng)，模糊控制策略有良好的魯棒性，因此根據(jù)上述智能汽車車隊的車車間距以及車速控制策略，建立智能車隊跟隨模型。把車速差(Δu)以及距離差(Δd)作為跟隨控制器的輸入，油門踏板開度以及制動踏板開度作為該控制器的輸出。

1) 模糊智能控制器輸入輸出量以及隸屬度函數(shù)的選擇

根據(jù)輸入量的特性，其隸屬函數(shù)選擇的是控制效率高、變化快的三角形隸屬函數(shù)。經(jīng)過多次調(diào)試模型，最終確定了車速差Δu(前一輛車的車速與后一輛車的車速的差值)最佳的論域范圍[-1 1]，其模糊子集分為7級，分別為：正大(PB)、正中(PM)、正小(PS)、零(Z)、負小(NS)、負中(NM)、負大(NP)。同理，經(jīng)過調(diào)試，距離差Δd(前一輛車的車頭到后一輛車車頭的距離)的論域為[0 1]，模糊子集分為4級，分別是：危險(N)、小(S)、中(M)、大(B)。該控制器的輸出分別為油門踏板開度和制動踏板開度，論域為[-1 1]，它們的模糊子集分為7級，分別是：正大(PB)、正中(PM)、正小(PS)、零(Z)、負小(NS)、負中(NM)、負大(NP)。當輸出值范圍為(0.1，1]，表明油門踏板信號輸出，當輸出值范圍為[-1，-0.1)，則表明制動踏板信號接入。考慮到減小油門和制動之間的切換次數(shù)，當輸出值為[-0.1，0.1]時，則表明踏板維持原來的狀態(tài)。考慮到輸入輸出量的特點，在模糊子集范圍內(nèi)，無明顯峰值，因此選擇正態(tài)分布型隸屬函數(shù)。

2) 模糊智能控制器控制規(guī)則

根據(jù)本文2.1節(jié)對跟車控制策略的描述，采用Mamdani’S(min-max)決策法，建立跟隨模型的控制規(guī)則，如表2所示。

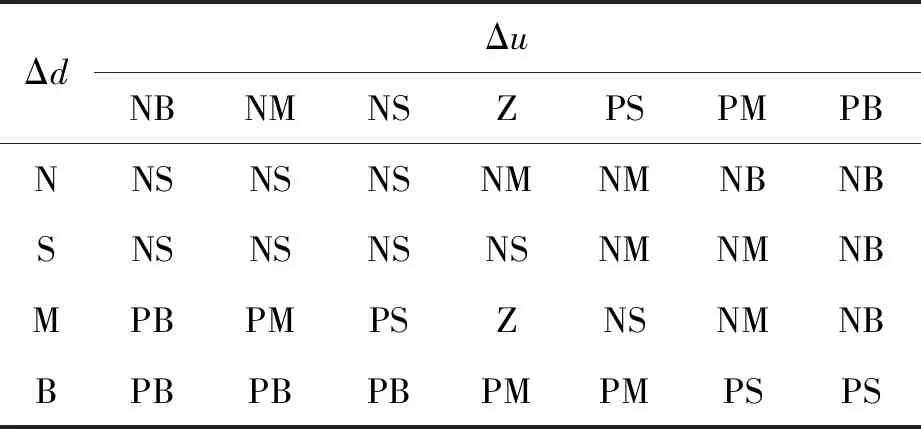
表2 規(guī)則變化

3 基于Matlab/Simulink/Stateflow建模以及仿真分析

3.1 智能車隊跟隨模型

基于上述對領(lǐng)航車的模型和跟車模型的分析，基于Matlab/Simulink仿真平臺下，搭建了有3輛車所組成的隊列行駛模型，如圖7所示。

本研究是由3輛同一款式的汽車構(gòu)成的車隊，其中領(lǐng)航車的駕駛員模型是根據(jù)自身的車速與目標車速的差值，以及差值的變化率，通過智能模糊控制方法(詳見第1節(jié)的結(jié)論)來判斷領(lǐng)航車的加速程度或者制動大小。1號跟隨車的駕駛員模型則需根據(jù)和領(lǐng)航車的速度差值以及和領(lǐng)航車的位移差值來判斷1號跟隨車的油門和制動踏板開度，1號跟隨車跟車模型如圖8所示。同理，2號跟隨車則是根據(jù)和1號跟隨車的相對速度以及相對距離來控制2號跟隨車的油門以及制動踏板的開度。

圖7 智能車隊跟隨模型

圖8 跟隨車駕駛員模型

3.2 仿真結(jié)果分析

在Matlab/Simulink搭建好模型后，車隊各個車輛之間車頭與車頭之間的初始間距為15 m，根據(jù)式(6)可知，車隊之間的安全距離隨著車速的增加而增加。領(lǐng)航車以ECE城市道路巡航工況的目標車速起步，ECE循環(huán)工況仿真時長為196 s。

車隊中各個車輛行駛速度隨時間的變化如圖9所示，圖中實線為領(lǐng)航車車速變化趨勢，點線為1號跟隨車車速變化情況，虛線為2號跟隨車車速變化情況。

分析圖9可知，車輛行駛速度變化曲線相似，2號跟隨車在某些時間節(jié)點出現(xiàn)了速度差異，分別是30、90、161.32和181.96 s，將該時間節(jié)點的車速進行對比，如表3所示。

圖9 隊列行駛車輛的速度變化

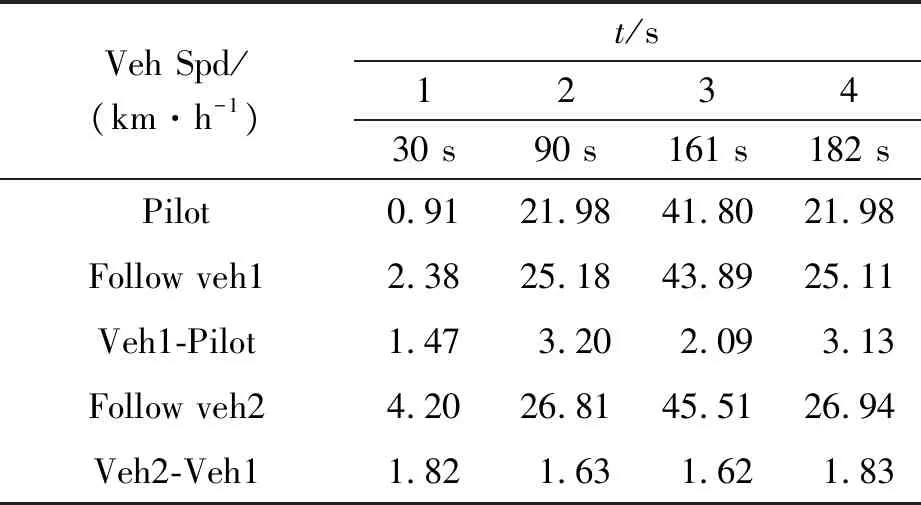
表3 車隊行駛特殊節(jié)點速度對比

通過表3的數(shù)據(jù)分析可知，在ECE城市道路循環(huán)工況下，最大車速差為3.2 km/h，小于車隊行駛車速差的要求，符合車輛隊列行駛的跟車車速目標范圍。

智能車隊在t=0時刻，各個車車頭間距以15 m為安全距離，在經(jīng)過ECE城市道路循環(huán)工況后，每輛車行駛距離隨時間的變化如圖10所示，圖中實線、點線和虛線分別為領(lǐng)航車、1號跟隨車、2號跟隨車的行駛距離變化曲線，可知在ECE城市道路工況下，車隊中的各個車輛間距保持較為一致，滿足了車隊通行效率的要求，其中在98.2、100、118、144.7 、190.2和191 s時間節(jié)點車車間距值較大。

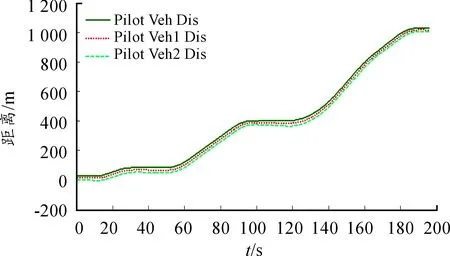
圖10 隊列行駛車輛的距離變化

記錄3輛車在上述6個節(jié)點所對應的行駛距離，詳細變化如表4所示。

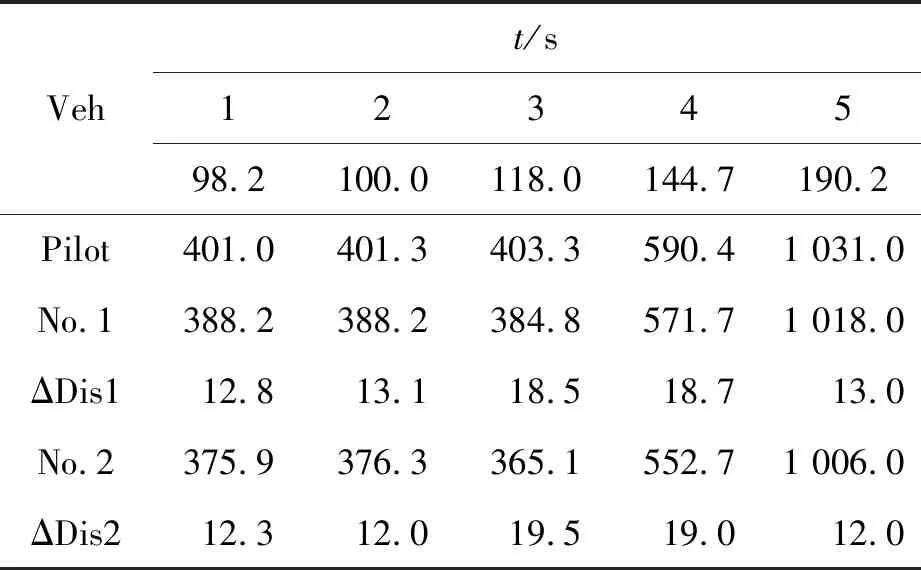
表4 隊列行駛車輛的距離(d)變化

表4中，ΔDis1代表領(lǐng)航車與1號跟隨車之間的距離差，ΔDis2代表1、2號跟隨車之間的距離差值。在ECE道路循環(huán)過程中，在98、100、190 s時刻，車隊兩兩車頭間距均有所減小，最近的情況保持在12 m。在118 s和114.7 s時刻，車車間距有所增加，最大車距保持在19.5 m。為了更好地描述車隊間距保持情況，計算了車車間距波動率，如表5所示。

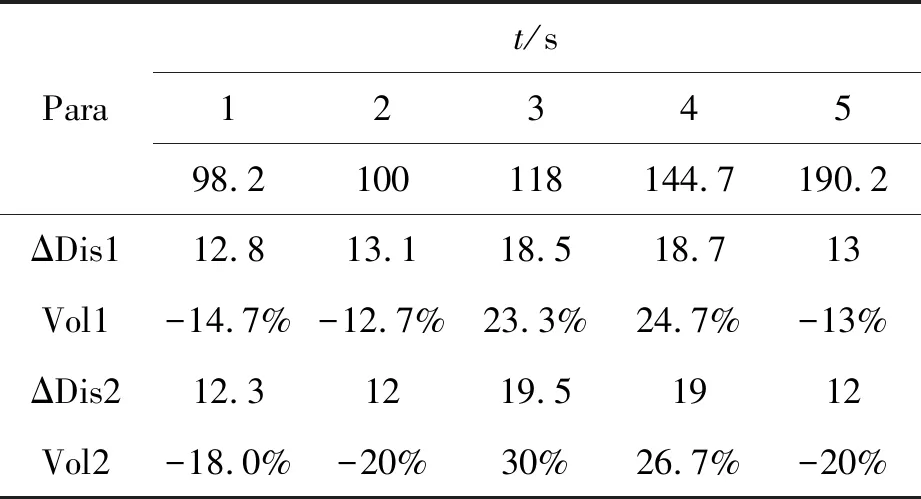
表5 隊列行駛車輛的距離(d)波動率

表5中，Vol1代表的是領(lǐng)航車與1號跟隨車間距的波動情況，Vol2代表的是1、2號跟隨車間距的波動情況，負值代表車車間距在靠近程度，正值代表車車間距在增加程度。

由表5可知，在ECE循環(huán)工況下，車車間距在靠近時的最大波動率為20%，在遠離時的最大波動率為30%，均小于或等于目標值，滿足車隊行駛時車車間距的要求。

4 結(jié)論

為了提高車隊行駛過程的安全和通行率，本文建立了車隊車輛跟隨模糊控制器、領(lǐng)航車駕駛模糊控制模型以及換擋模型模糊控制模型，并完成車隊縱向動力學建模，在給定的ECE城市道路循環(huán)工況下，基于Matlab/Simulink/Stateflow仿真平臺，對其進行了仿真分析，結(jié)果可知，車隊中的車輛行駛速度與領(lǐng)航車車速誤差值為3.2 km/h，行駛中各車間的距離保持在安全距離，在12～19.5 m。從仿真結(jié)果來看，2號跟隨車車速與1號跟隨車存在差值的原因有以下幾點：① 道路模型、車輛各系統(tǒng)模型的建立是采用的理想化的模型；② 模糊邏輯控制策略依賴大量的經(jīng)驗數(shù)據(jù)進行決策判斷，因此會導致結(jié)果誤差；③ 系統(tǒng)響應滯后，造成跟車反應遲滯；④ 未控制油門變化率，未考慮車輛隊列行駛時的能耗優(yōu)化。

基于以上分析，后續(xù)研究工作開展方向為：① 本次設(shè)計中未考慮復雜的實際環(huán)境以及非線性的動態(tài)特性，未來可以考慮。② 未來可以考慮深度學習等控制方法。③ 下一步針對混合動力汽車車隊能耗、通過率以及安全性綜合研究。