基于模糊集合理論的數(shù)學(xué)游戲設(shè)計(jì)

李宗雙，袁 華

1 模糊集合理論的概念及內(nèi)涵

集合是描述人腦思維對(duì)整體性客觀事物的識(shí)別和分類的數(shù)學(xué)方法，模糊集合論要求其分類要遵從模糊中聚排律的相關(guān)要求，在模糊集合對(duì)象的全體中，所有的集合元素必有一個(gè)特殊的屬性，屬A不含B，屬B不交A，要求這其中必有一個(gè)集合歸宿.所以，模糊集合理論的總體描繪特點(diǎn)是對(duì)一般概念的抽象概括，是對(duì)概念本身外延與歸納的高度整合，也可以說是要將其外化為具體的模糊概念，并借助MATLAB語言或編程來編輯概念及模型，最終在處理計(jì)算機(jī)語言中建立客體與概念的相關(guān)聯(lián)系，構(gòu)建一個(gè)模糊數(shù)學(xué)模型體系［1-2］.

模糊數(shù)學(xué)產(chǎn)生的直接動(dòng)力，與系統(tǒng)科學(xué)的發(fā)展有著密切的關(guān)系.在多變量、非線性、時(shí)變的大系統(tǒng)中，復(fù)雜性與精確性形成了尖銳的矛盾.LA扎德教授從實(shí)踐中總結(jié)出這樣一條互克性原理：“當(dāng)系統(tǒng)的復(fù)雜性日趨增長(zhǎng)時(shí)，我們作出系統(tǒng)特性的精確而有意義的描述的能力將相應(yīng)降低，直至達(dá)到這樣一個(gè)閾值，一旦超過它，精確性和有意義性將變成兩個(gè)幾乎互相排斥的特性.”這就是說，復(fù)雜程度越高，有意義的精確化能力便越低.復(fù)雜性意味著因素眾多，時(shí)變性大，其中某些因素及其變化是人們難以精確掌握的，而且人們又常常不可能對(duì)全部因素和過程都進(jìn)行精確的考察，只能抓住其中主要部分，忽略掉所謂的次要部分.這樣，在事實(shí)上就給系統(tǒng)的描述帶來了模糊性.“常規(guī)數(shù)學(xué)方法的應(yīng)用對(duì)于本質(zhì)上是模糊系統(tǒng)的分析來說是不協(xié)調(diào)的，它將引起理論和實(shí)際之間的很大差距.”因此，必須尋找到一套研究和處理模糊性的數(shù)學(xué)方法.這就是模糊數(shù)學(xué)產(chǎn)生的歷史必然性.模糊數(shù)學(xué)用精確的數(shù)學(xué)語言去描述模糊性現(xiàn)象，“它代表了一種與基于概率論方法處理不確定性和不精確性的傳統(tǒng)不同的思想，……，不同于傳統(tǒng)的新的方法論”.它能夠更好地反映客觀存在的模糊性現(xiàn)象.因此，它給描述模糊系統(tǒng)提供了有力的工具.

模糊集合理論，是指客體與概念之間，難以用具體的標(biāo)準(zhǔn)與規(guī)則來區(qū)分事物的存在狀態(tài).它具有內(nèi)涵和外延兩部分內(nèi)容，在內(nèi)涵中，模糊集合理論是強(qiáng)調(diào)客體間的對(duì)位聯(lián)系，而非強(qiáng)調(diào)事物的模糊性，它所要呈現(xiàn)的是一種對(duì)事物本身的判別與歸納，具有相對(duì)獨(dú)立性與不同步性；二是模糊數(shù)學(xué)的外延部分則產(chǎn)生于對(duì)概念本身及分類過程中所出現(xiàn)的界限與類別，模糊現(xiàn)象本身是客觀存在的，并沒有特定的歸納標(biāo)準(zhǔn)，但對(duì)于客體與概念的分化來講，它是具有分析與判別功能的.

2 利用模糊集合理論設(shè)計(jì)數(shù)學(xué)游戲模型

本文選用的是模糊集合中的二級(jí)模糊評(píng)判模型，需要通過四種反向的評(píng)價(jià)模型進(jìn)行預(yù)判設(shè)計(jì)，并對(duì)其中的每一個(gè)模型進(jìn)行抽樣處理，最終在綜合評(píng)價(jià)數(shù)據(jù)的基礎(chǔ)上進(jìn)行游戲設(shè)計(jì).

評(píng)價(jià)的基本原理是：首先確定評(píng)價(jià)對(duì)象的模型與數(shù)據(jù)集、建立聚合評(píng)判模型與評(píng)價(jià)因素，通過評(píng)價(jià)因素的權(quán)重集，分別確定評(píng)價(jià)的合理矩陣與綜合決斷集，同時(shí)利用運(yùn)算中的有效變量，對(duì)決斷集中的數(shù)據(jù)進(jìn)行權(quán)重分配，建立一個(gè)具體的矩陣集，并將其逐一代入兩邊的行列式，分別確定各個(gè)因素的權(quán)重及它們的評(píng)判矩陣，最后利用SPSS及MATLAB軟件定向處理數(shù)據(jù)，從而完成模糊數(shù)學(xué)模型的構(gòu)建與評(píng)價(jià).以下為具體的游戲模型設(shè)計(jì).

游戲模型一：給出綜合決策模型(h,d,a)，對(duì)權(quán)重分配A∈d(h)，對(duì)應(yīng)的綜合決斷h=a?d.A=(w1,w2,…,wn)，B=(q1,q2,…,qn)，h=(hij)ab，，簡(jiǎn)記為a=(∧?,∨?).其中h為評(píng)價(jià)因素的權(quán)重集，a為評(píng)判矩陣，d為綜合決斷集.

游戲模型二：評(píng)價(jià)因素T(h,d)，則Hi=

游戲模型三：評(píng)價(jià)因素T(a,d)，則Hi=游戲模型四：評(píng)價(jià)因素T(∧,-)，則Hi=

其中，運(yùn)算H為T的有效變量，即a+d=min(1,d+a) ，權(quán) 重 分 配，因此，即運(yùn)算h與普通加法一致.分析：加權(quán)平均模型T(-, +)，則a==1，fkj≤1，因而，其中運(yùn)算-與+一致.

基于上述定義建立模糊綜合評(píng)價(jià)數(shù)學(xué)模型.根據(jù)調(diào)查得出來的因素，采用綜合評(píng)判模型.游戲模型的權(quán)重分配數(shù)據(jù)如表1所示.

第一步，模糊綜合評(píng)價(jià)：按各因素等級(jí)進(jìn)行模糊綜合評(píng)價(jià).根據(jù)表1可以得到因素集和決斷集：T={A1,A2,A3,A4}={- +}.

第二步，確定評(píng)價(jià)因素的權(quán)重集為A=(0.12,0.21,0.3,0.48).

第三步，按四種模型運(yùn)算得模糊評(píng)價(jià)集B1和B2，其中，B1=A?R1，B2=A?R2.

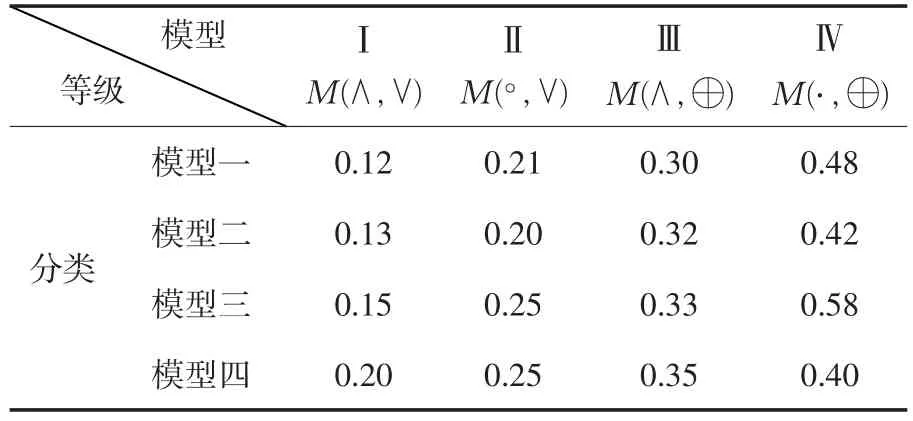
表1 四種模糊游戲模型的權(quán)重分配數(shù)據(jù)

假設(shè)對(duì)上述四種模糊游戲模型構(gòu)建成立，下面證明游戲模型的可行情況.

既然A的順序主子式全大于零，那么A1的順序主子式也全大于零.利用歸納法假定，A1是正定的，則存在可逆的n-1級(jí)矩陣G使G′A1G=En-1，這里En-1代表n-1級(jí)單位矩陣.

則A與E合同，因此，上述四種游戲模型是正定可行的.

第四步，利用MATLAB檢測(cè)數(shù)學(xué)游戲模型.

MATLAB程序如下：

＞＞clc

＞＞clear；

＞＞u=-100：1：100；

＞＞［x，y］=meshgrid（u）；

＞＞z=（2*x-y+11）/3；

＞＞u=0：pi/20：pi；

＞＞v=0：pi/20：2*pi；

＞＞［U，V］=meshgrid（u，v）；

＞＞x1=60*sin（U）.*cos（V）+3；

＞＞y1=60*sin（U）.*sin（V）-5；z1=60*cos（U）-2；

＞＞x2=40*sin（U）.*cos（V）-30；

＞＞y2=100*sin（U）.*sin（V）+20；

＞＞z2=10*cos（U）+100；

＞＞mesh（x，y，z）；

＞＞hold on

＞＞surf（x1，y1，z1）；

＞＞surf（x2，y2，z2）；

＞＞view（-40，16）

利用MATLAB判定空間圖形間的位置關(guān)系，設(shè)計(jì)數(shù)學(xué)建模，運(yùn)行游戲模型，在實(shí)際生活中有著廣泛的應(yīng)用.

3 模糊數(shù)學(xué)游戲模型在數(shù)學(xué)教學(xué)中的意義

模糊數(shù)學(xué)誕生至今已有50多年的歷史，它發(fā)展迅速、應(yīng)用廣泛.涉及計(jì)算數(shù)學(xué)、基礎(chǔ)數(shù)學(xué)、應(yīng)用科學(xué)、社會(huì)科學(xué)等多個(gè)方面［3］.其中，數(shù)學(xué)游戲在數(shù)學(xué)教學(xué)中具有重要的意義，所謂的數(shù)學(xué)游戲其實(shí)就是在游戲中添加一些數(shù)學(xué)知識(shí)，既可以讓學(xué)生在游戲的身臨其境中認(rèn)知數(shù)學(xué)知識(shí)，又可以讓學(xué)生在數(shù)學(xué)游戲的舉一反三中形成初步的數(shù)學(xué)思維與解決實(shí)際數(shù)學(xué)問題的能力.這種數(shù)學(xué)模型的應(yīng)用，不僅涉及數(shù)學(xué)知識(shí)的整合與學(xué)習(xí)，還具有一定的娛樂性和感染力［4］.

模糊數(shù)學(xué)游戲模型的建立具有重要的教學(xué)意義，對(duì)于授課主體的教師而言，模糊數(shù)學(xué)游戲模型的正向應(yīng)用可以促進(jìn)課程教學(xué)內(nèi)容的多項(xiàng)改革，更利于教學(xué)設(shè)計(jì)、課程導(dǎo)入、說課的理念轉(zhuǎn)變，提高學(xué)生課程的參與度與積極性，進(jìn)而促進(jìn)課堂教學(xué)水平與授課內(nèi)容的雙向提升［5］.同時(shí)，學(xué)生思維培養(yǎng)教育的方向會(huì)根據(jù)兒童不同的年齡階段有不同的側(cè)重，教師可以依據(jù)學(xué)生的聽課狀況來確定更加具體的教學(xué)內(nèi)容，科學(xué)合理地運(yùn)用模糊數(shù)學(xué)游戲模型，進(jìn)一步激發(fā)學(xué)生學(xué)習(xí)數(shù)學(xué)知識(shí)的興趣，最終促進(jìn)學(xué)生思維能力與綜合素質(zhì)的提升.