設(shè)計(jì)地震動(dòng)參數(shù)概率分布研究

程紹革　孫魁

摘要：基于地震危險(xiǎn)性理論分析框架，分析各類震源對(duì)地震動(dòng)參數(shù)分布的影響，建立地震動(dòng)參數(shù)分布函數(shù)，并采用蘆山地震動(dòng)傳播規(guī)律驗(yàn)證其工程通用性。基于等超越概率原則，提出不同后續(xù)使用年限設(shè)計(jì)地震動(dòng)參數(shù)計(jì)算方法。結(jié)果表明：地震動(dòng)參數(shù)分布函數(shù)服從極值Ⅱ型分布;地震動(dòng)參數(shù)累計(jì)分布函數(shù)可以用于不同后續(xù)使用年限設(shè)計(jì)地震動(dòng)參數(shù)取值，滿足現(xiàn)行規(guī)范要求。

關(guān)鍵詞：震源;地震動(dòng)參數(shù);極值Ⅱ型分布;后續(xù)使用年限;超越概率

中圖分類號(hào)：P315.91?文獻(xiàn)標(biāo)志碼：A?文章編號(hào)：1000-0666（2019）04-0579-05

0?引言

我國(guó)是一個(gè)地震災(zāi)害嚴(yán)重的國(guó)家，近年來(lái)先后遭遇了汶川8.0級(jí)地震、玉樹7.1級(jí)地震、盈江5.8級(jí)地震、雅安7.0級(jí)地震（溫瑞智等，2017）。2019年6月17日，四川長(zhǎng)寧發(fā)生6.0級(jí)地震（震源深度16?km）;6月18日，日本新瀉發(fā)生6.7級(jí)地震（震源深度10?km）。按照傳統(tǒng)評(píng)估經(jīng)驗(yàn)，日本新瀉地震災(zāi)情應(yīng)比我國(guó)地震災(zāi)情嚴(yán)重，但實(shí)際震害調(diào)查情況顯示四川長(zhǎng)寧地震震害更為嚴(yán)重。陸新征課題組（2019）分析認(rèn)為震害災(zāi)情受震級(jí)、地震動(dòng)強(qiáng)度和地面建筑抗震性能等諸多因素影響，因此僅僅依靠震級(jí)、震源深度和設(shè)防烈度難以進(jìn)行準(zhǔn)確的震害評(píng)估。地上建筑結(jié)構(gòu)損害主要受地面運(yùn)動(dòng)影響，因此研究分析場(chǎng)地地震動(dòng)參數(shù)受震級(jí)和震源距影響的概率分布，對(duì)于工程設(shè)計(jì)地震動(dòng)參數(shù)的取值具有重要參考價(jià)值。

當(dāng)前通用的烈度標(biāo)準(zhǔn)是通過(guò)對(duì)以往震害調(diào)查研究而形成的震害度量標(biāo)準(zhǔn)（胡聿賢，2016;中國(guó)地震烈度表，GB/T?17742—2008;明小娜等，2017），是基于人體感覺或建構(gòu)筑物的宏觀反映，并非可量化的指標(biāo)（非儀器烈度）。隨著社會(huì)生產(chǎn)生活對(duì)于建筑抗震性能需求的提高，結(jié)構(gòu)抗震性能不斷提升，不同時(shí)期烈度表對(duì)應(yīng)的地面運(yùn)動(dòng)參數(shù)也隨之發(fā)生明顯變化。各時(shí)期建筑作為時(shí)代文化的載體以多元化的形式并存，不同時(shí)期結(jié)構(gòu)出現(xiàn)設(shè)防烈度損傷對(duì)應(yīng)的地震動(dòng)參數(shù)存在明顯差異。而目前通用的設(shè)計(jì)地震動(dòng)參數(shù)取值方法是根據(jù)設(shè)防烈度確定的，難以確保抗震設(shè)防“三水準(zhǔn)”目標(biāo)的實(shí)現(xiàn)，尤其是使用年限非50年的建筑，如既有建筑等（周錫元等，2002;馬玉宏，謝禮立，2002;白雪霜，程紹革，2014）。為切實(shí)有效地對(duì)不同時(shí)期、不同類型結(jié)構(gòu)進(jìn)行抗震性能化加固改造，將基于設(shè)防烈度的地震動(dòng)參數(shù)取值轉(zhuǎn)化為直接基于設(shè)防地震動(dòng)參數(shù)的抗震設(shè)計(jì)更為合理，也更容易實(shí)現(xiàn)不同后續(xù)使用年限的性能化設(shè)計(jì)地震動(dòng)參數(shù)量化取值（高小旺，鮑靄斌，1985;雷拓等，2009;劉如山等，2009;馬玉宏，趙桂峰，2009;Zhou，Li，2011;張超，翁大根，2013）。

本文以地震危險(xiǎn)性理論分析框架為基礎(chǔ)（Cornell，1968），假定地震發(fā)生服從泊松分布，根據(jù)通用的震源距、震級(jí)以及重現(xiàn)周期與地震動(dòng)參數(shù)的統(tǒng)計(jì)回歸關(guān)系，建立基于重現(xiàn)期的設(shè)防地震動(dòng)參數(shù)取值計(jì)算公式，為不同后續(xù)使用年限設(shè)計(jì)地震動(dòng)參數(shù)取值提供參考。

1?震源對(duì)地震動(dòng)參數(shù)的影響

地震動(dòng)參數(shù)能夠反映地面運(yùn)動(dòng)的強(qiáng)弱程度，主要包括地震動(dòng)峰值加速度（PGA）、地面峰值速度（PGV）、持時(shí)（DSR）和譜速度（Sa），其中PGA和PGV是衡量設(shè)計(jì)地震動(dòng)強(qiáng)度的重要指標(biāo)，本文主要對(duì)這2個(gè)參數(shù)進(jìn)行研究分析，下文中的地震動(dòng)參數(shù)均指PGA和PGV。震源主要有點(diǎn)、線、面3種，建筑場(chǎng)地周圍可能存在一種或多種類型的震源，為確定周圍震源發(fā)震引起的場(chǎng)地最大地震動(dòng)參數(shù)概率分布，首先對(duì)每種類型震源引起的場(chǎng)地最大地震動(dòng)參數(shù)概率分布進(jìn)行分析。

1.1?點(diǎn)震源

由點(diǎn)震源發(fā)震引起的場(chǎng)地最大地震動(dòng)參數(shù)A與震級(jí)M、震源距R有關(guān)（Esteva，1964）：

式中：b1，b2，b3為擬合常數(shù)。

因此對(duì)于指定場(chǎng)地（即R=r），點(diǎn)震源發(fā)震引起的場(chǎng)地地震動(dòng)參數(shù)A大于設(shè)防地震動(dòng)參數(shù)A的概率P為：

式中：FM為震級(jí)累積分布函數(shù)。

Richter（1959）給出震級(jí)大于m的地震發(fā)生次數(shù)nm與震級(jí)m的關(guān)系：

式中：a，b為待定系數(shù)。由此可得：

式中：m≥m0，m0是一個(gè)極小震級(jí)（對(duì)于建筑抗震設(shè)防可以忽略的震級(jí)）;β=bln10。

將式（4）代入式（2），即為地震動(dòng)參數(shù)A的超越概率分布函數(shù)：

式中：C=exp[β（lnb1）/b2+m0）]，為與震級(jí)相關(guān)項(xiàng);Gp=r-βb3/b2，為場(chǎng)地位置項(xiàng)，p代表點(diǎn)震源;A為m0對(duì)應(yīng)的地震動(dòng)參數(shù)，A=b1eb2m0r-b3為設(shè)防地震動(dòng)參數(shù)下限。

以泊松計(jì)數(shù)過(guò)程作為地震發(fā)生概率模型已經(jīng)廣泛應(yīng)用于地震工程學(xué)研究中。研究表明（高小旺，鮑靄斌，1985;張超，翁大根，2013）：沿地震帶上地震的發(fā)生服從泊松分布，年平均發(fā)生率為v，在時(shí)間t內(nèi)發(fā)生地震次數(shù)為N的概率為：

在時(shí)間t內(nèi)，地震動(dòng)參數(shù)A超過(guò)設(shè)防地震動(dòng)參數(shù)下限A的次數(shù)為N的概率為：

式中：PA=P（A≥A）=CGPA-β/b2，為地震動(dòng)參數(shù)A超過(guò)設(shè)防地震動(dòng)參數(shù)下限A的概率;在時(shí)間t內(nèi)，地震動(dòng)參數(shù)Atmax小于設(shè)防地震動(dòng)參數(shù)下限A的概率等同于在時(shí)間t內(nèi)不發(fā)生大于設(shè)防等級(jí)的地震（N=0），即：

將式（5）代入式（8）可得地震動(dòng)參數(shù)A的累積分布函數(shù)：

假設(shè)點(diǎn)震源年發(fā)生震級(jí)大于4的地震概率為0.09，震源距為216?km。對(duì)于加速度，Esteva（1964）建議b1，b2，b3取值分別為2000，0.8，2;胡聿賢（2016）建議a，b分別取值5.87，0.696。代入式（5）可得C=2.4×109，Gp=4.7×10-10。將C，GP，b2，β=bln10=1.6帶入式（9）可得場(chǎng)地的加速度超越概率函數(shù)和重現(xiàn)周期為：

例如加速度2.25?gal的50年超越概率為63%，其重現(xiàn)周期為50年。當(dāng)然場(chǎng)地周圍潛在震源復(fù)雜，不可能只有一個(gè)。

1.2?線震源

當(dāng)建筑場(chǎng)地周圍存在線性震源時(shí)，如圖1所示，L為斷裂帶長(zhǎng)度，d為斷裂帶中點(diǎn)發(fā)生點(diǎn)源地震時(shí)的震源距，R為場(chǎng)地至斷裂帶端點(diǎn)距離，r為場(chǎng)地至斷裂帶上任意點(diǎn)距離。線震源可以看作是長(zhǎng)度為L(zhǎng)的連續(xù)點(diǎn)震源，斷裂帶上每一點(diǎn)發(fā)生震動(dòng)的概率均相等。因此由線震源發(fā)震引起的場(chǎng)地地震動(dòng)參數(shù)概率分布等于點(diǎn)源地震概率分布沿?cái)嗔褞L(zhǎng)的累積，即：

式中：fR（r）為震源距概率密度分布函數(shù)，可由震源距累積分布函數(shù)FR（r）求得：

式中：d≤r≤R。對(duì)r求導(dǎo)即為震源距概率密度分布函數(shù)：

式中：d≤r≤R。將式（14）代入式（12），則地震動(dòng)參數(shù)A的超越概率分布為：

式中：Gl為場(chǎng)地位置項(xiàng);l代表線震源;γ=βb3/b2-1;A≥b1eb2m0d-b3;C為震級(jí)相關(guān)項(xiàng)，見式（5）。

將式（15）代入式（8）可得地震動(dòng)參數(shù)A的累積分布函數(shù)：

式中：v^=ν/L，為地震帶每延米每年平均發(fā)震概率。

1.3?面震源

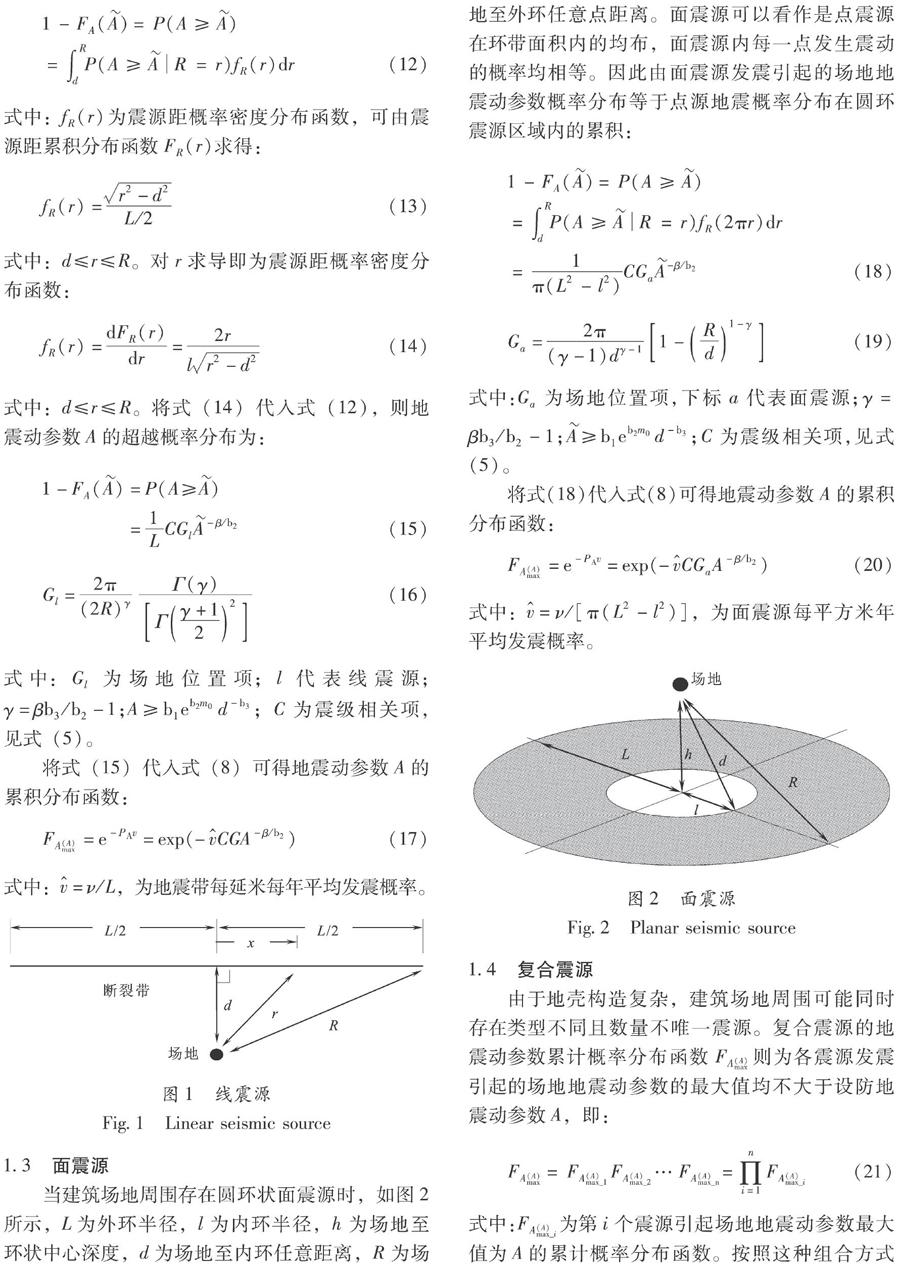
當(dāng)建筑場(chǎng)地周圍存在圓環(huán)狀面震源時(shí)，如圖2所示，L為外環(huán)半徑，l為內(nèi)環(huán)半徑，h為場(chǎng)地至環(huán)狀中心深度，d為場(chǎng)地至內(nèi)環(huán)任意距離，R為場(chǎng)地至外環(huán)任意點(diǎn)距離。面震源可以看作是點(diǎn)震源在環(huán)帶面積內(nèi)的均布，面震源內(nèi)每一點(diǎn)發(fā)生震動(dòng)的概率均相等。因此由面震源發(fā)震引起的場(chǎng)地地震動(dòng)參數(shù)概率分布等于點(diǎn)源地震概率分布在圓環(huán)震源區(qū)域內(nèi)的累積：

式中：Ga為場(chǎng)地位置項(xiàng)，下標(biāo)a代表面震源;γ=βb3/b2-1;A≥b1eb2m0d-b3;C為震級(jí)相關(guān)項(xiàng)，見式（5）。

將式（18）代入式（8）可得地震動(dòng)參數(shù)A的累積分布函數(shù)：

式中：v^=ν/[π（L2-l2）]，為面震源每平方米年平均發(fā)震概率。

1.4?復(fù)合震源

由于地殼構(gòu)造復(fù)雜，建筑場(chǎng)地周圍可能同時(shí)存在類型不同且數(shù)量不唯一震源。復(fù)合震源的地震動(dòng)參數(shù)累計(jì)概率分布函數(shù)FA（A）max則為各震源發(fā)震引起的場(chǎng)地地震動(dòng)參數(shù)的最大值均不大于設(shè)防地震動(dòng)參數(shù)A，即：

式中：FA（A）max_i為第i個(gè)震源引起場(chǎng)地地震動(dòng)參數(shù)最大值為A的累計(jì)概率分布函數(shù)。按照這種組合方式可以計(jì)算出類型、數(shù)量、深度隨機(jī)組合的符合震源影響下場(chǎng)地地震動(dòng)參數(shù)概率分布函數(shù)。上述震源相對(duì)于建筑場(chǎng)地均屬于對(duì)稱震源，對(duì)于非對(duì)稱震源可以采用同種類型反對(duì)稱震源進(jìn)行組合并計(jì)算。

2?地震動(dòng)參數(shù)概率分布

2.1?定性分析

真實(shí)的建筑場(chǎng)地通常位于復(fù)合震源影響范圍內(nèi)，其場(chǎng)地地震動(dòng)參數(shù)累計(jì)分布函數(shù)FA（A）max指數(shù)函數(shù)可以轉(zhuǎn)化為：

式中：地震動(dòng)參數(shù)A的指數(shù)（-β/b2）為負(fù)數(shù)，其中β，b2反映地震動(dòng)參數(shù)與震級(jí)和震源距，均為正數(shù)。可見，在復(fù)雜震源影響下，場(chǎng)地地震動(dòng)參數(shù)累計(jì)分布函數(shù)式（20）屬于極值Ⅱ型分布，極值Ⅱ型分布適用于具有下限、而無(wú)上限的分布，這與地震動(dòng)參數(shù)實(shí)際情況相符合。現(xiàn)有研究表明地震烈度屬于極值Ⅲ型分布，極值Ⅲ型分布適用于有上限的分布，這種分布符合地震烈度實(shí)際情況（人為規(guī)定烈度是有上限）。因此，直接根據(jù)場(chǎng)地地震動(dòng)參數(shù)概率分布函數(shù)和設(shè)防水準(zhǔn)計(jì)算設(shè)計(jì)地震動(dòng)參數(shù)更為準(zhǔn)確合理。

2.2?參數(shù)影響分析

在第一節(jié)各類型震源對(duì)場(chǎng)地地震動(dòng)參數(shù)分布影響分析中，假定了最大地震動(dòng)參數(shù)A與震級(jí)M和震源距R的關(guān)系，即式（1），這一假定可以根據(jù)研究進(jìn)展合理調(diào)整，例如溫瑞智等（2017）分析蘆山地震動(dòng)使用的傳播衰減關(guān)系，即：

式中：A為地震動(dòng)參數(shù);a1，a4為衰減項(xiàng)系數(shù);a2為擬合系數(shù);a3為場(chǎng)地放大系數(shù);ε為殘差;VS30為30?m覆蓋層平均剪切波速。假設(shè)a1是震級(jí)M的直接關(guān)系項(xiàng)，將式（23）帶入點(diǎn)震源式（5），可得：

式（24）中設(shè)防地震動(dòng)參數(shù)A的指數(shù)為負(fù)數(shù)，因此其場(chǎng)地地震動(dòng)參數(shù)累計(jì)分布函數(shù)仍屬于極值Ⅱ型分布，對(duì)于其他傳播衰減規(guī)律或復(fù)合震源同理可得相同結(jié)果。并且在第一節(jié)地震參數(shù)概率分布分析中所有參數(shù)均采用符號(hào)代替，沒有采用具體數(shù)值，避免了數(shù)值化差異，式（22）中地震動(dòng)參數(shù)A的指數(shù)為負(fù)數(shù)是定性結(jié)果，說(shuō)明第一節(jié)的分析結(jié)果具有較好的工程通用性。

3?地震動(dòng)參數(shù)概率分布應(yīng)用

對(duì)于使用年限小于50年的建筑，通常采用先折減烈度再確定設(shè)計(jì)地震動(dòng)參數(shù)的方法，這就難以從概率的角度保證三水準(zhǔn)設(shè)防目標(biāo)的實(shí)現(xiàn)，因?yàn)榱叶群偷卣饎?dòng)參數(shù)的概率分布具有明顯差異。因此，首先根據(jù)設(shè)防水準(zhǔn)和后續(xù)使用年限確定50年等效超越概率，再利用等效超越概率計(jì)算地震動(dòng)參數(shù)取值才是較為合理的計(jì)算方法。第一節(jié)分析結(jié)論顯示地震動(dòng)參數(shù)分布屬于極值Ⅱ型，即：

F（A）=exp-AσK（25）

式中：σ為超越概率為63.2%對(duì)應(yīng)的地震動(dòng)參數(shù)取值;K為形狀參數(shù)。

按照等超越概率原則，即結(jié)構(gòu)在后續(xù)使用年限內(nèi)與新建建筑保持相同的設(shè)防水準(zhǔn)超越概率，則其50年等效超越概率為：

式中：pi/T為抗震設(shè)防水準(zhǔn)i在T年內(nèi)的超越概率;i分別對(duì)應(yīng)小震、中震和大震，相應(yīng)的超越概率為63.2%，10%和2%～3%;將式（26）帶入（25）則可計(jì)算對(duì)應(yīng)的地震動(dòng)參數(shù)：

式中：形狀參數(shù)K可以根據(jù)規(guī)范取值（抗震規(guī)范GB?50010—2010中小震和中震形狀參數(shù)為-2.14）。通過(guò)地震動(dòng)參數(shù)區(qū)劃圖確定σ取值，采用式（27）建立場(chǎng)地地震動(dòng)參數(shù)概率分布函數(shù);以新建建筑為基準(zhǔn)，后續(xù)使用年限為30，40，50年的地震作用折減系數(shù)分別為0.79，0.9和1.0。也可以根據(jù)場(chǎng)地地質(zhì)構(gòu)造和周圍潛在震源分布情況建立合理的衰減關(guān)系并確定形狀參數(shù)K，采用式（21）建立場(chǎng)地地震動(dòng)參數(shù)概率分布函數(shù)。

4?結(jié)論

本文根據(jù)地震危險(xiǎn)性理論分析框架，分析了復(fù)合震源影響下場(chǎng)地地震動(dòng)參數(shù)概率分布，并對(duì)分析參數(shù)的適用性進(jìn)行闡述，采用蘆山地震動(dòng)傳播衰減關(guān)系驗(yàn)證了分析結(jié)果的通用性。基于等超越概率原則，給出了場(chǎng)地設(shè)計(jì)地震動(dòng)參數(shù)的計(jì)算方法，得到以下結(jié)論：

（1）單種或復(fù)合震源影響下，場(chǎng)地地震動(dòng)參數(shù)服從極值Ⅱ型分布，與烈度分布具有較大差別。

（2）場(chǎng)地地震動(dòng)參數(shù)累計(jì)分布函數(shù)可根據(jù)地震動(dòng)參數(shù)區(qū)劃圖采用式（27）建立，該方法計(jì)算簡(jiǎn)單、概念清晰，其可靠度滿足現(xiàn)行規(guī)范要求;對(duì)于具有長(zhǎng)期觀測(cè)統(tǒng)計(jì)資料的場(chǎng)地，也可以采用式（21）計(jì)算。

（3）地震動(dòng)參數(shù)累計(jì)分布函數(shù)可以用于不同后續(xù)使用年限設(shè)計(jì)地震動(dòng)參數(shù)取值;基于等超越概率原則，以新建建筑為基準(zhǔn)，后續(xù)使用年限為30，40，50年的設(shè)防地震動(dòng)參數(shù)折減系數(shù)分別為0.79，0.9和1.0。

參考文獻(xiàn)：

白雪霜，程紹革.2014.現(xiàn)有建筑抗震鑒定地震動(dòng)參數(shù)取值研究[J].建筑科學(xué)，30（5）：1-5.

高小旺，鮑靄斌.1985.地震作用的概率模型及其統(tǒng)計(jì)參數(shù)[J].地震工程與工程振動(dòng)，5（1）：15-24.

胡聿賢.2016.地震工程學(xué)[M].北京：地震出版社.

雷拓，錢江，蘇曉燕.2009.現(xiàn)役結(jié)構(gòu)抗震評(píng)估地震作用確定方法[J].沈陽(yáng)建筑大學(xué)學(xué)報(bào)（自然科學(xué)版），25（4）：620-624.

劉如山，胡少卿，鄔玉斌，等.2009.基于地震動(dòng)參數(shù)的結(jié)構(gòu)易損性表達(dá)方法研究[J].地震工程與工程振動(dòng)，29（6）：102-107.

陸新征課題組.連續(xù)反轉(zhuǎn)三次！我該怎么辦？從617宜賓6.0級(jí)地震和618日本6.8級(jí)地震談起[EB/OL].（2019-06-20）.[2019-06-29].https：//mp.weixin.qq.com/s/OPNfHJzHsVYpEQuwI0R0bA

馬玉宏，謝禮立.2002.考慮地震環(huán)境的設(shè)計(jì)常遇地震和罕遇地震的確定[J].建筑結(jié)構(gòu)學(xué)報(bào)，23（1）：43-47.

馬玉宏，趙桂峰.2009.確定現(xiàn)役結(jié)構(gòu)抗震加固設(shè)計(jì)地震動(dòng)參數(shù)的簡(jiǎn)化方法研究[J].工程抗震與加固改造，31（3）：78-83.

明小娜，周洋，鐘玉盛，等.2017.2017年云南魯?shù)镸S4.9地震房屋震害特征與烈度評(píng)定[J].地震研究，40（2）：295-302.

溫瑞智，任葉飛，王宏偉，等.2017.強(qiáng)震動(dòng)記錄分析與應(yīng)用-蘆山MS7.0地震為例[M].北京：地震出版社.

張超，翁大根.2013.震損建筑抗震鑒定加固中地震作用取值研究[J].建筑結(jié)構(gòu)學(xué)報(bào)，34（2）：61-68.

周錫元，曾德民，高曉安.2002.估計(jì)不同服役期結(jié)構(gòu)的抗震設(shè)防水準(zhǔn)的簡(jiǎn)單方法[J].建筑結(jié)構(gòu)，32（1）：37-40.

Cornell?C?A.1968.Engineering?seismic?risk?analysis[J].BSSA，58（5）：1583-1606.

Esteva?L.1964.Spectra?of?earthquakes?at?moderate?and?large?distances[J].Soc?Mex?de?Ing?Sismica，2：1-18.

Richter?C.1959.Seismic?regionalization[J].Bulletin?of?the?Seismological?Society?of?America，49（2）：123-162.

Zhou?X?L，Li?Y?M.2011.Study?on?Ground?Motion?Parameters?of?Seismic?Appraisal?for?Existing?Structures?Based?on?Residual?Service?Life[J].Advanced?Materials?Research，368-373：2303-2308.

GB/T?17742—2008，中國(guó)地震烈度表[S].

Discussion?on?the?Probability?Distribution?of?Design?Ground?Motion?Parameters

CHENG?Shaoge，SUN?Kui

（China?Academy?of?Building?Research，Institute?of?Earthquake?Engineering，Beijing?100013，China）

Abstract

Based?on?theoretical?analysis?framework?of?seismic?risk，the?probability?distribution?of?ground?motion?parameters?was?analyzed?incorporating?the?influence?of?all?potential?seismic?sources.And?Lushan?motion?was?used?to?verify?the?generality?of?the?analysis?results.Based?on?the?equal?exceeding?probability?principle，an?available?approach?was?proposed?to?determine?the?design?parameters?of?ground?motion?for?different?continuous?seismic?service?life，and?its?probabilistic?reliability?was?content?with?the?current?code.The?results?show?that?the?probability?distribution?of?ground?motion?parameters?was?embodied?by?Extreme?Value?Type?Ⅱ.The?method?for?determining?design?ground?motion?parameters?has?the?characteristics?of?simple?calculation?and?clear?concept.

Keywords：seismic?source;ground?motion?parameters;Extreme?Value?Type?Ⅱ;continuous?seismic?service?life;equal?exceeding?probability