基于混沌量子粒子群BP算法的研究

何曉云，許江淳，陳文緒

(昆明理工大學信息工程與自動化學院，云南 昆明 650500)

0 引言

近年來,反向傳播(back propagation，BP)算法已經成為機器學習理論中應用較為廣泛的網絡之一[1]。該算法采用誤差反向傳播的負梯度下降法，具有較好的非線性函數、自組織能力和泛化能力的特點，為良好預測能力奠定了基礎。但BP算法在預測中存在過度擬合[2]、預測精度不高的問題，當擬合精度越高，預測準確率就越低，即泛化能力差。其主要原因是：傳統的BP算法每次訓練的權值、閾值都不一樣，存在隨機性；然而，權值和閾值對于BP神經網絡的預測能力有很大的影響[3]。為了解決這一問題，國內外許多研究者提出了改進的方法。例如：Srivastava N[4]證明了加入隨機噪聲的數據集會使神經網絡的擬合性能變差，從而可提高泛化能力；防止對網絡學習過度是更有效的方法，即在樣本數據中添加正則項。王林[5]針對BP算法的權值和閾值隨機化、容易陷入局部收斂的特點，設計了一種優化BP神經網絡的自適應差分進化算法，避免了部分過擬合現象，但增大了算法的復雜度。

以上研究者提出的成果對于改進BP算法泛化能力的力度不大，導致BP算法預測模型在應用時出現其他問題[6]。因此，本文提出了一種基于混沌量子粒子群優化的BP(chaotic quantum particle swarm optimization BP，CQPSO-BP)算法。量子粒子群優化算法是用混沌序列來初始化種群的初始角[7]，針對粒子群算法的早熟收斂，引入了變異操作，提高了全局優化能力，從而優化BP神經網絡的權值、閾值。然后將它與BP算法結合，形成一種新的算法——混沌量子粒子群BP算法。最后，通過與改進的附加動量法和BP神經網絡作對比，利用不同的數據集進行預測試驗，將準確率、均方誤差(mean square error，MSE)、均方百分比誤差(mean square percent error，MSPE)作為評價指標[8]。試驗結果表明：CQPSO-BP算法在預測精度、收斂速度、準確率等方面，相對于傳統的BP神經網絡和改進的附加動量法等算法有較明顯的優勢。

1 BP神經網絡

BP神經網絡是一種多層饋型網絡[9]，主要依靠輸入信號的正向傳播和誤差的反向傳播，不斷調試網絡的權值和閾值，達到優化網絡的目的。訓練方法采用的是最速下降法traingd。

全局誤差函數為[9]：

(1)

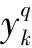
1.1 BP網絡的學習過程

①網絡初始化。設置BP網絡神經元之間的連接權值Wij、Wjk，確定網絡輸入層節點n個、隱含層節點數l個、輸出層節點數m個，以及隱含層和輸出層的閾值α[a1,a2,…,al]和b[b1,b2,…,bm]。

②計算隱含層的輸出。

(2)

式中：f為激勵函數；xi為輸入變量。

③計算輸出層的輸出。

(3)

④更新權值。

ωij(t+1)=ωij(t)+η[(1-β)D(t)+

βD(t-1)]i=1,2,…,n

(4)

ωjk(t+1)=ωjk(t)+η[(1-β)D′(t)+βD′(t-1)]

(5)

⑤更新閾值。

(6)

bk(t+1)=bk(t)+(yk-ok)

(7)

⑥判斷網絡訓練的誤差是否達到要求。若它達到期望的要求或設置的學習次數已用完，就結束網絡的訓練；否則，返回步驟②。

1.2 動量因子的優化算法

傳統的BP神經網絡存在收斂速度慢的問題。這主要是因為優化權值時，只根據某一時刻的負梯度方向進行修正，沒有考慮以前的修正經驗。這里引入了動量因子的方法。當權值陷入局部最小值時，會產生一個繼續向前運動的正向斜率。附加動量法的改進不僅考慮了誤差在梯度方向的作用[10]，還考慮了誤差曲面變化的趨勢。修正公式如下：

Δωij(n)=αΔωij(n-1)+(1-α)ηΔf[ωij(n-1)]

(8)

式中：Δωij(n)為權值修正量，且已經加入了修改的記憶方向；η為學習速率；n為訓練次數；α為動量因子，取值一般是0.1～0.8。

在BP算法中，提出了動量因子的改進后，可以有效改變網絡訓練的步長η，而不再是一個固定的值；同時，也可以改變修正權值的方向，即加入了一個擾動，有自動調節著步長的作用，可以向著平均的方向改變，從而不會產生太大的波動，并使誤差變小。總之，引入動量項可以加快網絡收斂速度，提高了預測的準確性。但是，其收斂速度相對還是太慢，預測效果存在一定的誤差。所以本文提出了混沌量子粒子群算法，以提高算法預測風速的準確性。

2 CQPSO-BP算法

量子粒子群(quantum particle swarm optimization,QPSO)算法容易陷入早熟收斂，即當一個粒子發現一個最優位置時，其他的粒子就會迅速向它靠攏。如果這個位置只是局部最優點，則算法就陷入了局部最優，出現早熟收斂。在QPSO算法中，對粒子的位置采用量子位的概率幅進行編碼，如式(9)所示：

(9)

式中：θ=2π×random,rondom為[0,1]之間的隨機數；i=1,2,…,n，n為種群數量；j=1,2,…,B,B為空間的維數。

粒子的位置移動按式(10)更新：

Δθij(k+1)=ωΔθij(k)+η1r1(Δθ1)+η2r2(Δθf)

(10)

式中:ω為慣性權重；η1、η2為學習因子；r1、r2為隨機數；Δθij為粒子在第j維的相位變化量；Δθ1為個體最優的相位變化量；Δθf為整個算法最優的相位變化量。

(11)

(12)

慣性權重ω的調整公式為：

(13)

式中:ωmax、ωmin分別為權值的最大值、最小值。

由于量子粒子群算法容易使粒子陷入早熟收斂，所以采用量子非門來加入變異操作，增加種群的遍歷性:

(14)

本文針對QPSO算法的遍歷性有限、容易陷入早熟收斂的特點，采用混沌的遍歷性和隨機性來彌補，即混沌量子粒子群優化(chaotic quantum particle swarm optimization,CQPSO)算法。該算法利用隨機性產生B個參數(θ1,θ2,…,θB)，然后產生運動軌跡。每一個軌跡有n個序列，形成n×B個初始角。根據Logistic映射形成的混沌序列為：

x(k+1)=μx(k)[1-x(k)]

(15)

式中:x為混沌變量，x?(0,1)且x≠0.25、0.5、0.75;μ為控制參數。

3 CQPSO-BP算法的預測模型

3.1 數據集描述

由于輸入變量和輸出變量的量綱不統一，為了減小網絡的誤差，歸一化的計算是必要的。它可以使數據之間的關系更容易體現，則預測的風速更準確。這里采用最大值最小值法，使所有變量限定在[0，1]之間。

為了驗證CQPSO-BP算法預測能力的有效性，共選擇3組不同維度的屬于工業、教育和商業等行業的公開的數據集。運行在Windows10，8.00 GB內存，Inter(R) Core(TM) i7-8550U CPU @ 1.80 GHz環境下，基于Matlab R2019a中完成。

3.2 評價指標

為了評價本文建立的3種模型的預測性能，預測正確率至關重要。預測的準確率越高，誤差越小，算法預測性能越好。本文選擇準確率和3種評價指標來評價3種模型的預測性能，分別是準確率、MSE和MSPE。計算公式如下：

(16)

(17)

式中：N為測試樣本個數；αi為第i個測試樣本的實際值；βi為第i個測試樣本的預測值。

3.3 CQPSO-BP算法流程

CQPSO-BP算法的主要流程如下。首先，輸入樣本數據，初始化種群的規模和變量數量，生成混沌初始化種群。其次，根據輸入變量的個數，決定BP網絡的結構，并初始化適應度值——即用 CQPSO-BP算法的粒子位置向量編碼BP算法的權值和閾值中的相關參數，評價函數為網絡的均方誤差的倒數，以計算出網絡的最優適應度值。再次，評價最優適應度值，判斷有沒有達到要求的精度或最大迭代次數。如果達到，則獲得最優的權值、閾值。最后，判斷網絡誤差是否滿足預設要求，滿足則輸出預測值，不滿足則算法繼續迭代。同理，如果最優適度值沒有達到要求，則算法繼續迭代，直到達到預設要求為止。

CQPSO-BP算法流程如圖1所示。

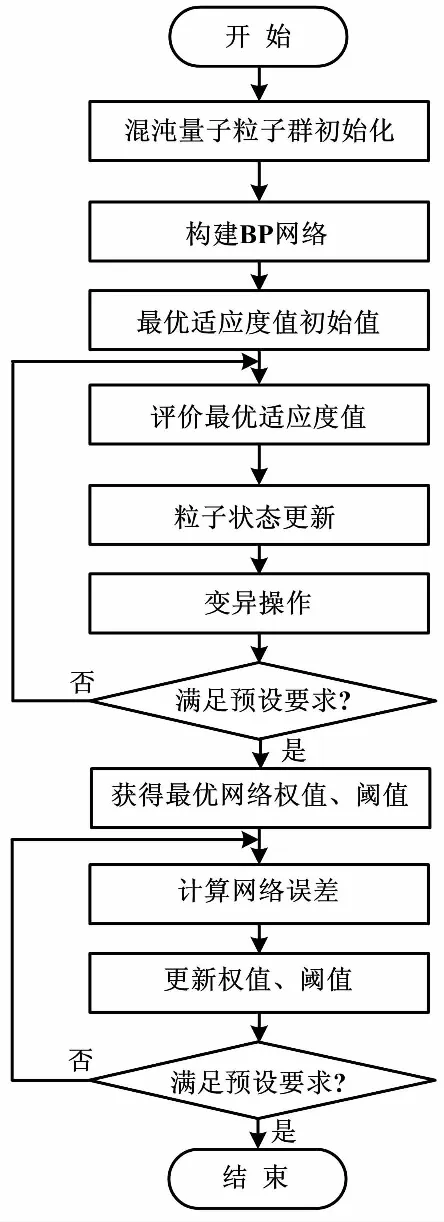
圖1 CQPSO-BP算法流程圖

3.4 仿真結果及分析

本文的數據來源于公開的、不同維度的數據集。在工業領域中，本文選擇電力負荷的公開數據集，根據系統的運行特性、自然條件和社會影響等，預測未來某一時刻的負荷數據。該數據集維度是3。在教育領域中，選擇從印度的角度預測研究生入學率的數據集，入學率就是被承認的機會，影響因素有GRE分數、托福成績、大學評級、SOP、LOR、CGPA、研究成果，該數據集維度是7；在商業領域中，選擇某商店中葡萄酒質量的樣本數據集，影響的因素有顏色、溫度、葡萄品種、土壤等，該數據集維度是11。三個數據集分別有1 200組、960組、1 020組數據，選擇其中的200組、80組、60組數據作為測試樣本。

在BP神經網絡中，預測模型的每個神經元對應的作用函數為Sigmoid型函數，隱含層的作用函數為S型正切函數tansig，輸出層的作用函數采用S型對數函數logsig。在網絡中，訓練的最大次數為1 000；訓練要求的精度為1e-3；訓練的學習速率為0.01。

本文中的輸入變量根據維度選取，所以輸入層設置為維度個數，根據Kolmogorov定理，網絡中間層的神經元可取(2n+1)個，n為輸入層神經元(維度)，輸出變量有1個，所以輸出層個數為1個。混沌量子粒子群算法的種群規模為20，最大迭代次數為60，慣性權重ωmax=0.9、ωmin=0.6,控制參數μ=0.36，學習因子c1=c2=2，變異概率為0.05。在Matlab平臺上建立3種算法模型，然后分別仿真輸出3種模型在電力負荷、研究生入學率、葡萄酒質量等級的預測結果對比。

電力負荷預測和實際電力負荷對比圖、研究生入學率預測和實際入學率對比圖、葡萄酒質量預測和實際葡萄酒質量對比圖，分別如圖2、圖3、圖4所示。

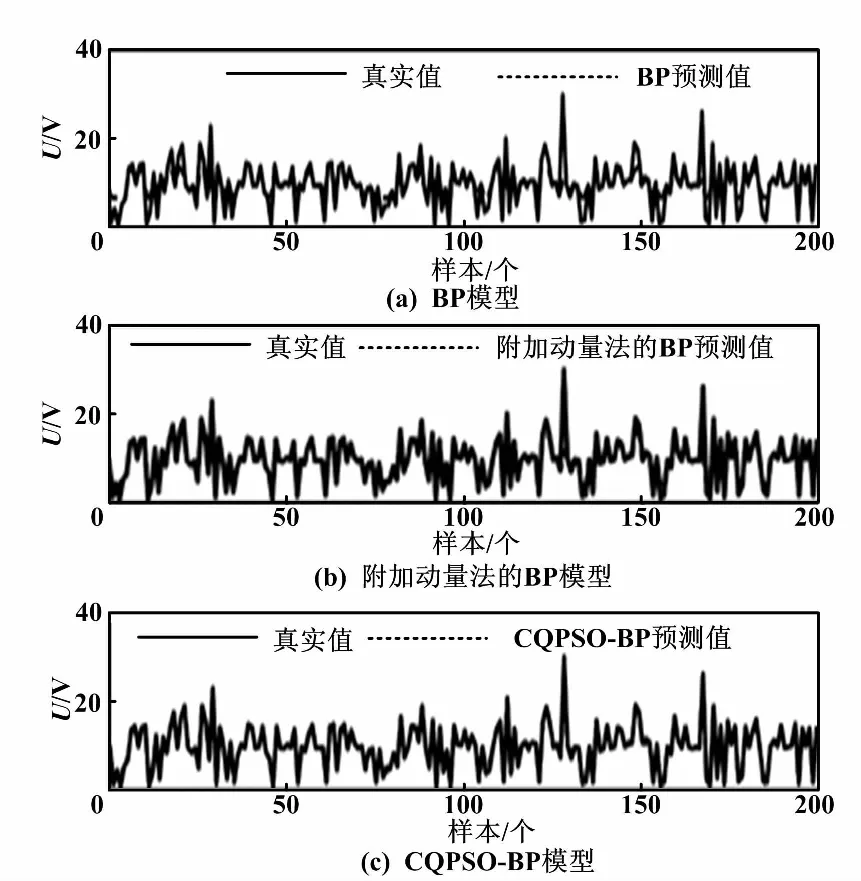
圖2 電力負荷預測和實際電力負荷對比圖

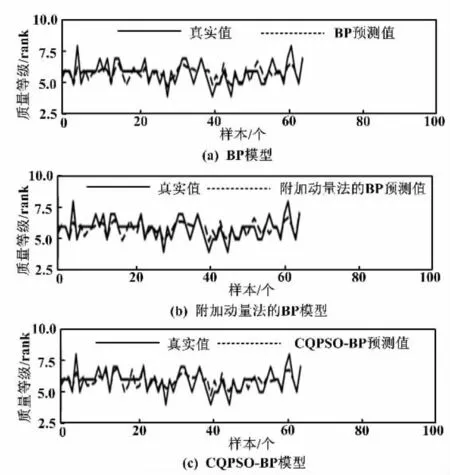
圖3 研究生入學率預測和實際入學率對比圖

Fig.3 Comparison of graduate enrollment rate prediction and actual enrollment rate

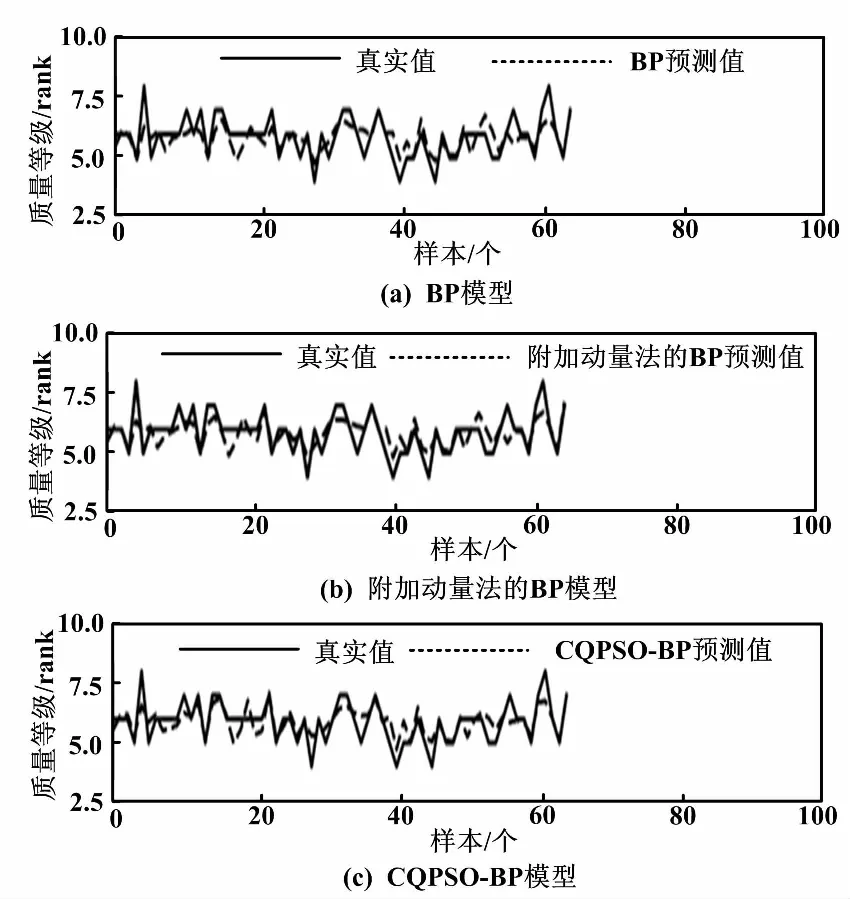
圖4 葡萄酒質量預測和實際葡萄酒質量對比圖

從圖2～圖4可以直觀地看到，相比于傳統的BP神經網絡和改進的附加動量法，CQPSO-BP算法的預測效果有較明顯的優勢，而BP算法的預測效果是相對較差的。CQPSO-BP算法有較強的抗過擬合能力。3種模型在訓練方法上都有所不同，預測的精度都不同。電力負荷預測的維度是3，研究生入學率預測的維度是7，葡萄酒質量預測的維度是11。在不同維度下，相同算法預測精度也不同。因為數據的不同，會影響預測效果。但CQPSO-BP算法的預測效果都是相對較好的，說明CQPSO-BP算法適用于預測模型。

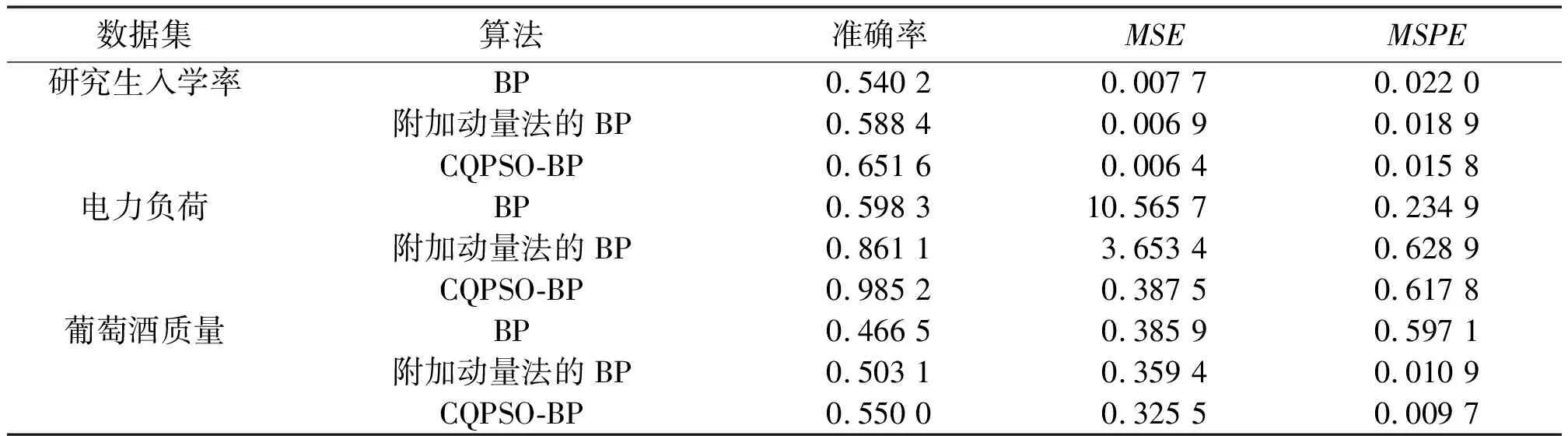
表1 3種算法的預測性能對比分析

表1中：準確率最大值為98.52%；MSE最小值為0.006 4；MSPE最小值為0.009 7。這3個評價指標的最優值都是在CQPSO-BP算法訓練時取得。又因為電力負荷數據集的預測效果相對較好，預測值基本跟蹤實際值，準確率最高。因此，選擇這一組數據集來分析3種算法的的訓練誤差變化。誤差曲線如圖5所示。

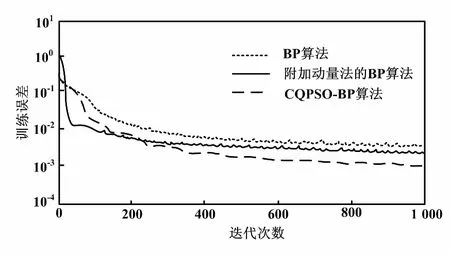
圖5 3種算法的訓練誤差曲線圖

從圖5可以直觀地看到，在電力負荷的預測模型中，當迭代次數最大值設為1 000時，BP算法的誤差曲線圖總體下降得較慢；在200步時開始更緩慢地下降；在1 000步時還沒有收斂。通過附加動量法的BP算法改進后，該算法訓練誤差曲線圖開始下降得較快，整體的訓練誤差比BP算法更接近預設要求。CQPSO-BP算法的訓練誤差相對下降得較快，在接近940步時達到收斂，完成訓練，且此時誤差達到預設要求為0.001。因此，CQPSO-BP算法的收斂速度最快，誤差相對較小。

4 結束語

本文針對傳統BP算法存在的過度擬合和預測精度不高的問題，提出了一種混沌量子粒子群BP算法。該算法將CQPSO算法與BP算法相結合，提高了種群的遍歷性。用混沌序列初始化粒子的初始角位置，并引入變異操作，避免網絡進入早熟收斂，從而對BP神經網絡的權值和閾值進行優化。通過與附加動量法的BP算法和傳統的BP算法進行對比，證明了CQPSO-BP算法的預測效果相對附加動量法和BP神經網絡有明顯的優勢，也說明了CQPSO-BP算法有抗過擬合能力。在測試階段，準確率、MSE、MSPE的最優值都是在CQPSO-BP算法訓練時取得的。CQPSO-BP算法模型是適用于研究預測問題的一種模型，具有實際應用價值。