考慮層間接觸狀態的橫觀各向同性結構動力響應解析解

顏可珍　滿建宏　石挺魏　陳帥　劉能源

摘? ?要：基于線彈性體動力學基本方程，結合坐標變換、Buchwald勢函數，建立了移動荷載作用下層狀橫觀各向同性結構的動力控制方程，利用傅里葉變換及其微分性質得到了在Fourier變換域內單層有限厚度剛度矩陣和半空間無限體剛度矩陣. 考慮層間接觸條件組裝各剛度矩陣得到總剛度矩陣，并根據邊界條件求解總剛度矩陣在變換域內的解. 然后，進行Fourier逆變換將變換域內的解轉化為物理域內的解. 通過與已有文獻結果的對比驗證了本文理論推導的正確性，隨后通過參數的變化來模擬層間接觸狀態的改變，并分析了面層與基層層間接觸狀態對路面結構動力響應的影響. 計算結果表明：基、面層層間接觸狀況越差，路面結構的整體性耐久性越差.

關鍵詞：層間接觸;橫觀各向同性層狀結構;移動荷載;動力響應;Fourier變換

中圖分類號：TU470;TU311? ? ? ? ? ? ? ? ? ? ?文獻標志碼：A

Analytical Solution for Dynamic Response of Transversely Isotropic

Structures Considering the State of Interlayer Contact State

YAN Kezhen，MAN Jianhong，SHI Tingwei，CHEN Shuai，LIU Nengyuan

（College of Civil Engineering，Hunan University ，Changsha 410082，China）

Abstract：Based on the basic equations of linear elastodynamics， combined with the coordinate transformation and Buchwald potential function， the dynamic governing equations for a transversely isotropic multilayered pavement under moving loads are developed. The stiffness matrix for a single layer with a finite thickness and a half-plane are derived by using Fourier transform and its differential properties. Considering the interlayer conditions between layers， the global matrix are assembled with the analytical layer element of each layer. The solutions in the integral transform domain are obtained by combining with the boundary conditions. Then， the corresponding solution in the frequency domain is further recovered by applying inverse Fourier transform. The theoretical derivation of this paper is verified by comparing with the results of the existing literature. The change of interlayer conditions between layers is then simulated by changing parameters. The influence of the interlayer conditions between the surface layer and base layer on the dynamic response of the pavement structure can be calculated and analyzed. The calculation results show that the poor interlayer condition between the adjacent structure layers can cause the poor overall performance and durability of the pavement structure.

Key words：interlayer contact;transversely isotropic multilayered structure;moving load;dynamic response;Fourier transform

在許多工程實例中，以運動形式存在的荷載并不少見，例如行駛中的車輛、運行中的高鐵、地鐵等，它們都會造成接觸面狀態的改變. 此外，我國現行的規范將層狀彈性體系各層間的接觸狀態假設為完全連續狀態，但該假設并不符合層間真實的接觸狀態. 對于兩種完全不同的材料（比如路面結構中瀝青面層和無機結合料基層），它們二者之間的接觸狀態往往處于半連續半光滑的狀態，因此結構設計中假設層間接觸狀態為完全連續是不合理的. 故研究層間接觸狀態對層狀彈性體系的動力響應影響顯得格外重要. 并且，我國現行的《公路瀝青路面設計規范》中是以靜荷載來作為設計荷載，但是眾多學者研究表明以靜荷載作為設計荷載往往高估了路面的使用壽命，且運動荷載更易造成路面結構的破環. 目前，國內外許多學者針對移動荷載作用下的動力響應進行了大量研究. 王春玲等[1]利用Laplace變換和雙重Fourier變換得到了地基在移動荷載下的動力響應;左迎輝等[2]采用傅里葉級數的方法求得了移動荷載下Gibson地基模型中各點的動力響應，并討論了土體的剪切模量、荷載移動速度等對豎向位移的影響;張昀青等[3]利用Duhamel積分和Fourier變換求得了移動荷載作用下半空間無限體動力響應的表達式，為交通荷載作用下的土體動力響應分析提供了一定的理論基礎;司理濤等[4]采用虛擬激勵法和廣義Duhamel求解了移動荷載作用下粘彈性半空間體動力響應的積分形式解，并分析了荷載移動速度對動力響應的影響;周鳳璽等[5]采用半解析的方法求解出了非均勻地基的解答，并討論了荷載移動速度、非均勻參數和剪切模量對動力響應的影響，通過算例表明土體各點豎向位移與非均勻參數和剪切模量成反比，與荷載移動速度成正比;蔣建群等[6]通過Fourier變換求解了移動集中荷載作用下彈性半空間響應的積分形式解，并對其穩態響應進行了數值分析，研究了荷載移動速度、觀測點深度和觀測點距離等參數對動力響應的影響;艾智勇等[7]針對以往求解層狀地基的數值方法，提出了一種新的方法即解析層元法. 該方法不僅大大地提高了計算效率，還有效地避免了計算過程中發生的數值溢出現象，具有較高的計算效率和數值穩定性. 艾智勇等[8-9]采用該方法對層狀地基進行了大量研究，例如荷載移動速度、土層的成層特性和地基的加固效果等對地基動力響應的影響;劉能源等[10]采用有限元數值分析方法分析了層間結合條件對加鋪層受力狀況的影響;宋小金等[11]等研究了行車速度與不同深度下荷載響應持續時間的關系;莊妍等[12]研究了移動荷載作用下結構安定性問題，發現移動荷載對結構有著重大的影響;詹永祥等[13]研究了運動荷載對孔隙水壓力的影響;顏可珍等[14]采用譜元法研究了運動荷載下多層結構的動力響應，通過與靜荷載的對比發現：運動荷載比靜荷載產生更大的動力響應，更易造成結構的不穩定狀態. 因此研究運動荷載下多層結構的動力響應對完善我國設計規范有著重要的參考價值.

上述對于移動荷載作用下地基動力響應的研究都是基于層狀彈性體系各層間的接觸狀態為完全連續狀態，但在實際工程建設中的土基、路面等通常是分層鋪筑，層與層之間由于材料的差異性和施工條件、工藝等因素的影響，層間接觸狀態幾乎不可能做到完全連續狀態，因此分析運動荷載下層狀彈性體系各層間的接觸狀態對結構動力響應的影響更加符合實際，對完善我國《公路瀝青路面設計規范》也有重要的參考價值. 目前，國內已有的解析方法僅能計算層間接觸狀態在完全連續或完全光滑下的動力響應，且容易出現數值溢出的現象. 對于不同層間接觸狀態下的結構動力分析主要依靠Abaqus有限元軟件來計算，雖然計算結果較準確，但是計算一次需要大量的時間成本. 解析解的優點在于計算速度快、便于參數分析，值得注意的是求解層狀彈性體系在不同層間接觸狀態下的動力響應解析解卻鮮有研究. 因此，本文的目的是開發一種快速高效的解析法來研究不同接觸狀態的層狀橫觀各向同性結構在移動荷載作用下的動力響應. 該解析法的指數項為負項，很好地避免了指數溢出的現象，并通過參數的變化來模擬層間接觸狀態的改變，由此分析層間接觸狀態對層狀彈性結構設計的各項指標的影響.

1? ?單層應力和位移分量推導

1.1? ?基本方程

以路表中心為原點建立總坐標系OXZ，以荷載中心為原點建立局部坐標系OiXiZi，如圖1所示. 分布長度為2b的條形荷載P作用在路表面，并以速度c勻速運動，則該問題可簡化為平面問題. 橫觀各向同性彈性體在總坐標系OXZ下的平面問題動力方程、物理方程、幾何方程可參考文獻[8].

引入Buchwald勢函數Φ、Ψ，其中Φ反映等容波勢函數，ψ反映剪切波勢函數. 由兩個勢函數Φ、 ψ表示的位移、應力方程為：

如圖1所示，X-Z為固定坐標系，為了簡化計算，此處將引入移動坐標oxz，其中x = X - ct，z = Z，并分別用ux、uz來表示移動坐標系下水平方向和豎直方向的位移，通過坐標變換得出：

另外，在移動坐標系下勢函數？椎、Ψ對時間t的微分表達式和應力、位移對x、z的微分表達式如下：

式中：σx、σz和τxz為移動坐標系下平面的應力分量.

為了求解方程（4），應用傅里葉變換，實現二階偏微分方程從物理域到積分變換域的轉換. 方程（4）變換后如下所示：

求解微分方程（5）可得：

其中：

χ（ξ）=ν（θξ）2-（1+k2）]2-4k2[k3（θξ）4-（1+k3）（θξ）2]

ν = 1 + k2k3 -k32

式中：ei是對角指數矩陣;θi是待定系數列矩陣;Ki為4×4的已知系數矩陣. 表示如下：

k11 = k13 = iξβ1? ? k12 = k14 = iξβ2? ? k21 = -k23 = -λ1k22 = -k24 = -λ2k31 = k33 = （c33λ21 - c13 ξβ1）k32 = k34 = （c33λ22 - c13 ξβ2）k41 = -k43 = -λ1c44iξ（β1 + 1）k42 = -k44 = -λ2c44iξ（β2 + 1）? ? ?（10）

θi = [Ai? ?Bi? ?Ci′? ?Di′ ]T? ? ? （12）

1.2? ?層間接觸條件

傳統的路面結構分為面層、基層、底基層和土基4個部分，面層又分為上面層、中面層和下面層. 由于施工方法和施工條件的差異會導致層與層之間的接觸有時并非完全連續. Matsui等[15]采用剪切彈簧模擬相鄰層狀結構層之間的界面滑移，并通過Bisar驗證了該方法的正確性. 故本文采用下式來表示層間接觸條件：

（1-αix）{uix（ξ，hi）-ui+1x? ? （ξ，0）} = αixβixτixz（ξ，hi）

（13）

式中：αix為層間滑移系數，其值在0～0.99之間變化.當該值為0時，表示層間接觸狀態為完全連續狀態;當該值為0.99時，表示層間接觸狀態無限接近光滑狀態. b為荷載寬度，βix的表達式如下：

則第i層和第i+1層的狀態分量關系為：

式中：

Ci = 1? ?0? ?0? ?-αixβix/（1 - αix）0? ?1? ?0? ? ? ? ? ? ?00? ?0? ?1? ? ? ? ? ? ?00? ?0? ?0? ? ? ? ? ? ?1

由式（9）和式（15）得：

（Kimi）θi = （CiKi+1ni+1）θi+1? ? ? ?（16）

式中：mi和ni+1分別表示每一層層底和下一相鄰層層頂的對角指數矩陣.

Ki = Ki+1 = K11? ? K12? ? K13? ? K14K21? ? K22? ? K23? ? K24K31? ? K32? ? K33? ? K34K41? ? K42? ? K43? ? K44

1.3? ?邊界條件

假設多層結構表面作用為恒定速度移動的荷載P（x），荷載寬度為b，則：

P（x） = P（x），x≤b/20，? ? ? x≥b/2? ? ? （17）

故邊界條件可寫成

σZ（x，0，t） = P（x）τXZ（x，0，t） = 0? ? ? （18）

對σZ（x，0，t）進行傅里葉變換可以得到：

σZ（x，0，t） = -P（x）sin（ξb）/ξb? ? （19）

多層結構體系的最底層為半空間無限體，即當z→∞時：

uZ（x，z，t）z→∞ = ux（x，z，t）z→∞ = 0Cn（ξ） = Dn（ξ） = 0 Cn′（ξ） = Dn′（ξ） = 0? ? （20）

所以多層結構的最底層（半空間無限體）只有兩個待定系數，即：

θn′ = [An? ?Bn]T? ? ? ? ? ? ? ? ? ? ? （21）

1.4? ?多層結構總剛度矩陣的建立

總剛度矩陣（22）是由式（16）重復組合形成的對角矩陣，該矩陣充分考慮了層間接觸條件：

式中：Dn，Ki，CiKi+1均為與層間條件有關的已知系數矩陣;D0是與層間條件無關的系數矩陣，表達式如下：

D0? = K31? K32? K33? K34K41? K42? K43? K44 z=0，Dn = K11? ? K12K21? ? K22K31? ? K32 K41? ? K42? z=0（23）

總剛度矩陣由4（n-1）+2個矩陣組成，即小矩陣的個數等于待定系數的個數. 由式（22）可以求解每個待定系數，然后可以求得各層在傅里葉變換域內的動力響應解答，最后通過逆變換求得在物理域內的解答.

2? ?數值計算與分析

2.1? ?算法驗證

為了驗證本文解析方法的正確性，算例采用文獻[2]中的結構模型參數和運動荷載參數. 取橫觀各向同性系數n = 1，即橫觀各向同性模型轉化成各向同性均質模型，其中E = 290 MPa，μ = 0.45，ρ = 1 650 kg/m3，h = 5 m，荷載長度2b = 4 m，荷載大小為P =400 kPa，荷載速度c = 20 m/s[2]. 圖2表示在移動荷載中心處，地基中豎向位移隨土體深度變化的曲線，并與文獻[2]的計算結果進行對比. 另外，采用參考文獻[9]的模型計算參數，其中，n = Eh /Ev，m = Gv /Ev，Cr = ，Mr = c /Cr，uz′ = uzGv /pb，取值Mr = 0.5. 算例采用4層結構模型，各層m取值均為0.4，μh和μvh均取值為0.25. Case3各層參數如下：n1 = 3，n2 = n3 = 2，n4 = 1;Case4各層參數如下：n1 = n2 = n3 = n4 = 1. 按照本文的方法進行計算并與文獻[9]的結果進行比較，計算結果如圖3所示. 從圖2、圖3中可以看出，本文算法的計算結果與文獻的結果基本吻合，從而驗證了本文方法的正確性.

為了更好地說明該解析法適用于分析多層彈性體系層間接觸的問題，本文將計算結果與Abaqus的計算結果進行對比. Abaqus模型采用C3D8R單元，模型尺寸取6 m（X向、縱向）×5 m（Y向、橫向）×5 m（Z向、豎向），荷載以恒定速度沿X方向移動，如圖4所示. 邊界條件：與X方向垂直的兩個面的X向位移為0;與Y方向垂直的兩個面的Y向位移為0;模型底部為完全固定. 荷載的大小取0.7 MPa，移動速度為10 m/s，荷載長度為22.78 cm，寬為15.68 cm. 模型各結構層參數如下：Evi = 1 550、1 500、50 MPa;Ehi = 775、1 500、50 MPa;μvi = μvhi = 0.25、0.25、

0.4;ρi= 2 300、2 100、1 800 kg/m3;Gvi= 580、620、20 MPa;hi = 0.18 m、0.38 m、∞ （i = 1，2，3）.

有研究[16-17]表明采用摩擦系數能夠很好地模擬路面各結構層間的接觸狀態. 當摩擦系數f小于0.4時，層間接觸狀態較差;當摩擦系數f接近于1時，層間接觸狀態較好. 故該Abaqus模型僅考慮面層與基層的層間接觸狀態，其他層間接觸狀態為完全連續. 取摩擦系數f = 0.5來表示半光滑半連續的中間接觸狀態，對應的滑移系數為0.5. 表1列出了Abaqus模型模擬結果與本文解析方法的計算結果.

從表1可以看出，2種計算方法在2種接觸狀態下的計算結果分別相差1.72%和2.27%，這種誤差都是在工程誤差的允許以內. 對比2種方法的計算耗時，可以發現本文的解析法大大節約了計算時間，這有利于節約時間成本. 故本文針對層間接觸問題提出的解析方法具有準確、高效的優點.

2.2? ?層間接觸條件的影響

本文建立4層的橫觀各向同性路面典型結構，路面各層厚度及基本材料特性見表2. 假設荷載移動速度為20 m/s，荷載寬度a = 23 cm，荷載大小

P（x）=0.7 MPa. 在橫觀各向同性路面中，面層和基層均考慮為橫觀各向同性體，面層和基層的橫觀各向同性系數（即水平方向的彈性模量Eh與豎直方向的彈性模量Ev的比值）分別為n1和n2，其值均為0.4.

在2017年最新頒布的《公路瀝青路面設計規范》中，將瀝青混合料層層底拉應變、無機結合料穩定層層底拉應力和路基頂面豎向壓應變作為瀝青路面的設計指標，其對應的力學響應分別為行車方向的水平拉應變、行車方向的水平拉應力和豎向壓應變. 另外，路表彎沉是直接反映路面強度的一個重要指標.

本文將著重研究面層與基層的層間接觸狀態對路面動力響應的影響. 另外，其他層與層之間的接觸狀態均考慮為完全連續狀態. 面層與基層的層間接觸狀態用滑移系數α來表示，當α取值為0時，表示完全連續狀態;當α取值為0.99時，表示完全光滑狀態.

2.2.1? ?層間接觸條件對路表彎沉的影響

彎沉是指路面在荷載作用下的豎向變形，它反映了路面結構的整體剛度. 路表彎沉值越小，表明路面結構的整體性越好，剛度越大，路面的抗變形能力越好.

由圖5可知，隨著滑移系數的增大，路表彎沉不斷增大，滑移系數為0.99（即完全光滑）時的路表彎沉明顯大于其他狀態的路表彎沉. 完全光滑時的路表彎沉比完全連續（即滑移系數為0）時的路表彎沉大4.75%. 其他接觸狀態相比于完全連續狀態的路表彎沉分別增大1.39%、1.62%、2.35%和2.96%. 由此可知層間接觸狀態對路面結構的整體性有較大的影響，層間接觸狀態越好，整體性越好，抗壓入能力越強，彎沉值越小. 因此，若將路面結構看做完全連續會高估路面結構的整體性強度，對結構設計不利.

2.2.2? ?層間接觸條件對面層底部應變的影響

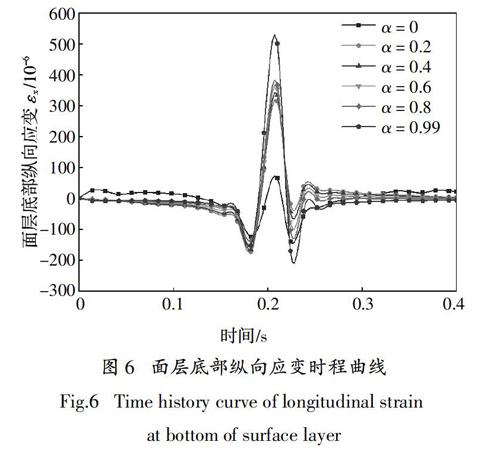
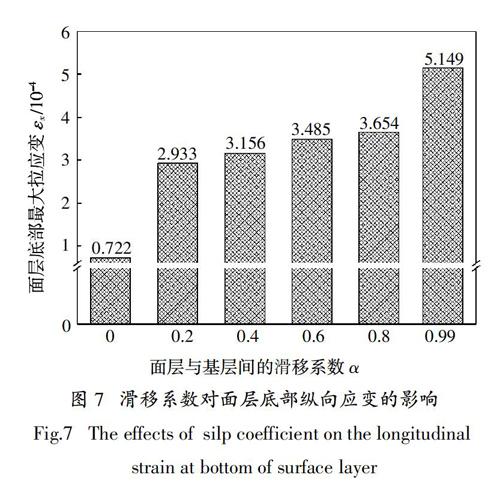
我國《公路瀝青路面設計規范》將瀝青混合料的層底拉應變作為一個重要的設計指標. 瀝青面層層底拉應變與路面結構的使用性能關系密切，過大的層底拉應變可能導致路面產生橫向裂縫，影響路面的正常使用. 不同層間接觸條件對面層層底拉應變的影響如圖6、圖7所示.

由圖6可知，不同接觸條件下面層底部縱向應變時程曲線基本類似，在荷載移動過程中，縱向應變由壓應變慢慢變為拉應變，最后再變為壓應變，最后變為零. 當荷載移動到測點的正上方時，應變值最大且為受拉狀態. 正是由于這種拉壓的反復狀態，使得路面可能產生疲勞開裂. 由圖7可知，隨著滑移系數的減小（接觸狀態逐漸變好），面層底部的縱向應變峰值逐漸減小. 完全連續狀態的縱向應變明顯小于非完全連續狀態，而完全光滑時的縱向應變明顯大于非完全光滑狀態.

2.2.3? ?層間接觸條件對基層底部拉應力的影響

基層底部拉應力是控制基層疲勞開裂的重要指標，我國《公路瀝青路面設計規范》亦將基層底部拉應力作為一個重要的設計指標. 不同層間接觸狀態對基層底部拉應力的影響如圖8所示.

由圖8可知，雖然隨著滑移系數的增大，基層底部的拉應力在變大，但是完全光滑時的基層底部拉應力僅比完全連續時大4.84%，故層間接觸條件對基層底部拉應力影響不大.

2.2.4? ?層間接觸條件對土基頂部壓應變和壓應力的影響

我國《公路瀝青路面設計規范》將土基頂面豎向壓應變作為一個重要的設計指標，它亦是評價路面性能的重要指標，并且土基頂部過大的壓應變會造成車轍、沉陷等路面病害，因此，研究土基頂部的豎向壓應變顯得十分重要. 滑移系數對土基頂部豎向壓應變的影響如圖9所示.

由圖9可知，隨著滑移系數的增大，土基頂部豎向壓應變的峰值逐漸增大. 在非連續狀態下，增大的趨勢并不明顯，增大的幅度均在5%以內. 當結構層為完全連續時，土基頂部豎向壓應變比非完全連續時依次減小38.2%、39.1%、39.4%、40.2%和44%. 可見，在非連續狀態時，層間接觸條件對土基頂部豎向壓應變的影響不大，而在完全連續時，土基頂部豎向壓應變明顯小于非連續狀態. 故在進行路面結構設計時將路面結構看成完全連續狀態可能會導致路面在早期使用階段出現車轍或者沉陷等病害，進而縮短路面的使用壽命.

圖10分析了不同滑移系數下，土基頂部豎向壓應力的變化情況. 從圖中可以看出土基頂部豎向壓應力的峰值和壓應變峰值一樣，均隨著滑移系數的增大而增大. 在非連續狀態下，變化不明顯且增長幅度均在3%以下. 非完全連續狀態下的最大豎向壓應力比完全連續狀態時依次增大了38.8%、39.2%、39.7%、40%和43%，可見，在非連續狀態時，層間接觸條件對土基頂部豎向壓應力的影響不大，而在完全連續時，土基頂部豎向壓應力明顯小于非連續狀態. 因此，層間接觸狀態的變壞會加劇工后長期的變形，導致路面結構的破壞，降低路面使用壽命.

3? ?結? ?論

1）本文依據彈性動力學理論，結合坐標變換、傅里葉變換和層間接觸條件推導出多層橫觀各向同性結構的解析解. 該解析解的總剛度矩陣考慮了層與層之間的接觸狀態，避免了連續剛度矩陣和光滑剛度矩陣的變換，并且Abaqus在計算層間接觸時會耗費大量的時間，而本文的解析解計算速度非常快，大約只需2 min，這大大節約了時間成本，便于實際工程的應用. 本文的理論推導采用剪切彈簧模型來模擬層間接觸狀態，對于層狀彈性體系計算的發展具有重要的參考價值.

2）算例計算表明，層間接觸狀況對路面結構的動力學響應影響顯著. 層間接觸狀況越差，路面結構的整體性越差，抗壓入能力也會越差，導致路表彎沉增大，進而面層底部縱向應變、基層底部拉應力和土基頂部的豎向應變和壓應力也會變大. 因此在路面結構設計時若將路面結構看做完全連續結構會高估路面結構的整體性強度和疲勞壽命，對結構設計不利并減少路面的使用壽命.

3）本文求解移動荷載作用下層狀橫觀各向同性結構動力響應的方法，具有較好的計算效率和數值穩定性，并且很好地避免了解析法在計算時數值溢出的缺點. 因此在以后三維結構及粘彈性結構計算中可以進行考慮.

參考文獻

[1]? ? 王春玲，黃必成，曹彩芹. 移動荷載下彈性半空間地基上矩形薄板的動力響應解析研究[J]. 土木工程學報，2016，49（1）：116—121.

WANG C L，HUANG B C，CAO C Q. Analytical study on dynamic response of rectangular thin plate on an elastic half-space under moving loads[J]. China Civil Engineering Journal，2016，49（1）：116—121. （In Chinese）

[2]? ? 左迎輝，徐長節，蔡袁強. 移動荷載下下臥基巖Gibson地基的動力響應[J]. 振動工程學報，2005，18（3）：351—354.

ZUO Y H，XU C J，CAI Y Q. Dynamic analysis of Gibson soil medium on bedrock under moving load[J]. Journal of Vibration Engineering，2005，18（3）：351—354.（In Chinese）

[3]? ? 張昀青. 移動荷載作用下半無限體的動力響應解[J]. 巖土力學，2004，25（6）：955—957.

ZHANG Y Q. Dynamic response of semi-infinite body under moving loads[J]. Rock & Soil Mechanics，2004，25（6）：955—957. （In Chinese）

[4]? ? 司理濤，趙巖，張亞輝. 移動隨機線源荷載作用下黏彈性半空間體的動力響應[J]. 工程力學，2016，33（6）：98—106.

SI L T，ZHAO Y，ZHANG Y H. Adynamic response of viscoelastic half-space subjected to moving random line loads[J]. Engineering Mechanics，2016，33（6）：98—106.（In Chinese）

[5]? ? 周鳳璽，曹永春，趙王剛. 移動荷載作用下非均勻地基的動力響應分析[J]. 巖土力學，2015，36（7）：2027—2033.

ZHOU F X，CAO Y C，ZHAO W G. Analysis of dynamic response of inhomogeneous subgrade under moving loads[J]. Rock & Soil Mechanics，2015，36（7）：2027—2033.（In Chinese）

[6]? ? 蔣建群，周華飛，張土喬. 彈性半空間體在移動集中荷載作用下的穩態響應[J]. 巖土工程學報，2004，26（4）：440—444.

JIANG J Q，ZHOU H F，ZHANG T Q. Steady-state response of an elastic half-space under a moving point load[J]. Chinese Jounal of Geotechnical Engineering，2004，26（4）：440—444.（In Chinese）

[7]? ? 艾智勇，劉文杰，任廣鵬，等.基于解析層元法的成層半平面地基移動荷載動力響應研究[J].巖土工程學報，2018，40（2）：237—242.

AI Z Y，LIU W J，REN G P，et al. Dynamic response of a multilayered half-plane under moving loads with the analytical layer-element method[J].Chinese Journal of Geotechnical Engineering，2018，40（2）：237—242.（In Chinese）

[8]? ? AI Z Y，ZHANG Y F. Plane strain dynamic response of a transversely isotropic multilayered half-plane[J]. Soil Dynamics & Earthquake Engineering，2015，75：211—219.

[9]? ? AI Z Y，REN G P. Dynamic analysis of a transversely isotropic multilayered half-plane subjected to a moving load[J]. Soil Dynamics & Earthquake Engineering，2016，83：162—166.

[10]? 劉能源，顏可珍，胡迎斌. 基于橫觀各向同性的瀝青路面加鋪層力學分析[J]. 湖南大學學報（自然科學版），2017，44（5）：96—103.

LIU N Y，YAN K Z，HU Y B. Mechanical analysis of asphalt concrete overlay over old asphalt pavements considering cross-anisotropy properties[J]. Journal of Hunan University（Natural Sciences），2017，44（5）：96—103.（In Chinese）

[11]? 宋小金，樊亮. 移動荷載作用下瀝青路面應力響應的持續時間[J]. 湖南大學學報（自然科學版），2018，45（7）：71—76.

SONG X J，FAN L. Durations of stress response in asphalt pavement under moving load[J]. Journal of Hunan University（Natural Sciences），2018，45（7）：71—76. （In Chinese）

[12]? 莊妍，王孟，王康宇. 移動荷載作用下結構彈塑性安定分析方法及其應用研究[J]. 湖南大學學報（自然科學版），2018，45（7）：93—102.

ZHUANG Y，WANG M，WANG K Y. Study on shakedown analysis method of elastic-plastic structures under moving loads structures and its application[J]. Journal of Hunan University（Natural Sciences），2018，45（7）：93—102. （In Chinese）

[13]? ZHAN Y X，YAO H L，ZHANG J B，et al. Dynamic analysis of pavement and multi-layered transversely isotropic saturated ground system subjected to a rectangular moving load[C]//Mechanics and Mechanical Engineering. Chengud：The 2015 International Conference on Mechanics and Mechanical Engineering（MME 2015）， 2015：118—126.

[14]? YAN K Z，SHI T W，YOU L Y.Spectral element method for dynamic response of multilayered half medium subjected to harmonic moving load[J]. International Journal of Geomechanics ，2018，18（12）：04018161.

[15]? MATSUI K，MAINA J W，INOUE T. Axi-symmetric analysis of elastic multilayer system considering interface slips[C]//International Symposium on Maintenance & Rehabilitation of Pavements & Technological Control Segundo Simposio Sobre Manutencao E Rehabilitacao De Pavimentos E Controle Technologico. Auburn，2001：122—129.

[16]? 鄭仲浪. 重載車輛作用下瀝青路面層間力學行為研究[D]. 西安：長安大學工程機械學院，2010：58—78.

ZHENG Z L. Study on interfacial mechanical behavior of asphalt pavement under heavy vehicle loading [D] .Xi'an：School of Engineering Machinery，Chang′an University，2010：58—78. （In Chinese）

[17]? 劉紅坡. 層間接觸對半剛性瀝青路面力學響應的影響[D]. 成都：西南交通大學土木工程學院，2006：35—43.

LIU H P. Aanlaysis on the merchanical response of semi-rigid base pavement with contact model [D] .Chengdu：School of Civil Engineering，Southwest Jiaotong University，2006：35—43.（In Chinese）