活動中探究 探究中思考

錢英 蔣曉鳳

[摘? ?要]復習課是讓學生進行知識梳理歸納、形成思想方法的重要課型.而幾何復習課更是要有積累幾何問題解決的基本圖形、基本思想方法和基本活動經驗的重要功能.

[關鍵詞]平行線;復習課; 活動 ;探究

[中圖分類號]? ? G633.6? ? ? ? [文獻標識碼]? ? A? ? ? ? [文章編號]? ? 1674-6058（2019）32-0005-02

一、教材分析

《平行線》這一章的主要內容是平行線的概念和畫法;同位角、內錯角、同旁內角的概念;平行線的判定和平行線的性質，初步認識圖形平移變換.仍保留實驗幾何的特點，但對推理判斷有了進一步的要求.

二、教學目標

知識與技能：鞏固平行線一章的相關概念;靈活運用平行線的判定和性質解決問題.

過程與方法：在三角板與直線的擺放過程中，解決簡單的數學問題，發現一般規律.

情感態度與價值觀：感受生活中的數學，感受動態中蘊含的規律性東西.

三、教學重難點

教學重點：靈活運用平行線的判定和性質解決問題.

教學難點：在歸納過程中進行由特殊到一般的推理.

四、教學過程

1.創設情境，復習基礎

問題1：怎樣的兩條直線是平行線？你能畫平行線嗎？

活動1：如圖1，已知直線a，過直線a外一點P作直線b，使a//b.

（學生在活動紙上推平行線，請一位學生板演）

問題2：判斷a//b的依據是什么？你能不能和同桌說一說你的作圖依據？

【設計意圖】根據推平行線作平行線，在實際操作中復習平行線的判斷.

問題3：已知a//b，你可以得到什么結論？

生：a與b平行……（支支吾吾說不出）

師：a//b的條件下有很多話想說，可看著這個圖形又說不出來.

生：再添一條直線就好了.

師：說得真好！平行線被第三條直線一截就能發揮出無窮的威力，所以，我們經常添加這樣的輔助線.（畫直線c與a、b相交）現在，你能得到什么？

總結：此刻我們的條件是已知直線平行.而學生脫口而出的是由角的關系得到線的關系，是平行線的判定.而現有條件是a//b，需要由線的關系轉化為角的關系，是平行線的性質.平行線的判定與性質實現了角的關系與線的關系的相互轉化.

【設計意圖】讓學生感受平行線的判定與性質間的關系，從而在解決問題時能根據實際情況選擇使用.

2.動手操作，判定平行

師：這節課我們就運用平行線的性質與判定來解決與三角板有關的問題.（板書課題）來看這副三角板，它有很多的秘密，來說說已經被我們揭曉的秘密有哪些？（先拿出三角板，再說邊、角的特征）

活動2：直線a、直線b與三角板擺放成如圖2和圖3所示.

（1）如圖2，若含30°角的三角板的斜邊與直線a垂直，且∠1=60°，能否說明a//b？

（2）如圖3，若含45°角的三角板的兩條直角邊分別平分了一組同旁內角，能否說明BC//DE？

問題4：通過審題你得到了哪些信息？

問題5：題中告訴我們的都是角的信息，而需要得到的卻是線的關系，我們需要怎么做呢？

問題6：如何得到這些特殊的角的關系呢？

【設計意圖】在三角板背景中，發現問題的本質，熟練運用平行線的判定.

3.動態歸納，運用平行

師：若得到了兩直線平行，那么就能解決更多的問題.

活動3：

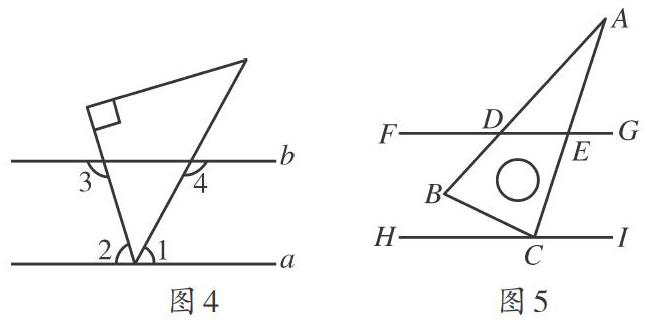
1.已知a//b，用含45°角的三角板擺放成如圖4所示，若∠1=50°，則∠2=_________，∠3=________，∠4=________.

2.已知FG//HI，用含30°角的三角板擺放成如圖5所示，若∠ACI=50°，能否求出圖中出現的部分角的度數，并尋找它們之間的數量關系？

（1） ∠B=________，∠BDF=________，∠BCH=________，關系為________________;

（2）∠B=________，∠BDG=________，∠BCI=________，關系為________________;

（3）∠A=________，∠ADG=________，∠ACI=________，關系為________________;

（4）∠A=________，∠ADF=________，∠ACH=________，關系為________________.

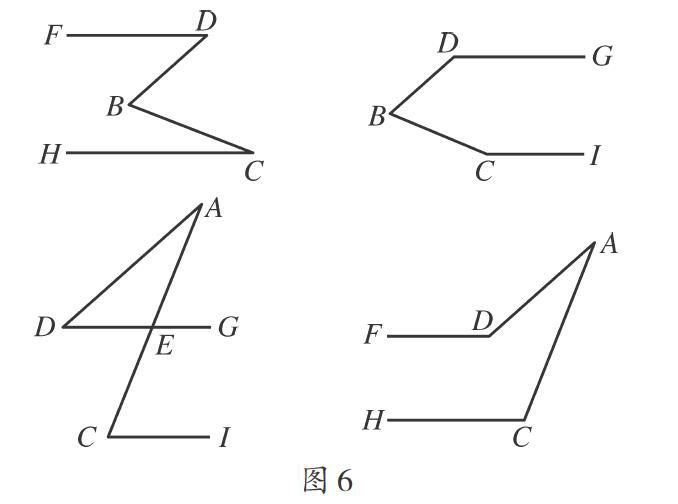
請學生分析完成，嘗試分析得出圖中的各個角的度數，從中抽象出如圖6所示的四個基本圖形，得到此時三個角之間的數量關系.

問題7：改變∠ACI的度數，但要使點B在平行線間，點A在平行線外，得到的結論是否依舊成立？脫離三角板，結論是否依舊成立？選一個基本圖形進行說理.

【設計意圖】在運用平行線的性質時，由題中的特殊情況歸納總結出一般規律，并對猜想進行說理.

4.反思總結，歸納提升

師：本節課我們再認識了平行線，從角的關系與線的關系的轉化角度，再次認識平行線的判定與性質，感受了轉化思想方法和特殊到一般的歸納方法.

5.相互編題，鞏固練習

師：請你利用直線、三角板等素材，編一道與平行線有關的題目考考你的同桌.

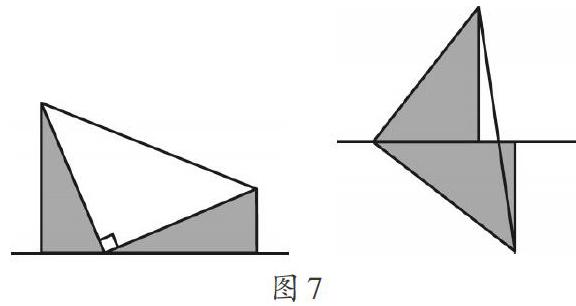
其實，直線與三角板能玩出很多的花樣.如圖7，三角板在擺動過程中，始終有兩個三角形的形狀、大小保持相等，當然這是我們后續要繼續研究的.

【設計意圖】讓學生在探索中發現三角板與平行線之間的無窮妙處，為未來的“全等”學習做好鋪墊.

（責任編輯 黃桂堅）