農業輪式機器人PI魯棒-滑模控制—基于RBF神經網絡

曹 東，閆銀發，宋占華，田富洋，趙新強，劉 磊，王春森，李法德，陳為峰

(山東農業大學 a.機械與電子工程學院/山東省園藝機械與裝備重點實驗室;b. 資源與環境學院，山東 泰安 271018)

0 引言

隨著機器人技術的迅速發展，農業機器人承擔越來越繁重的任務，促使農業輪式機器人機械多體系統逐漸向著柔性機器人方向發展，系統變得越來越復雜，自由度也逐漸變多。這就要求復雜的農業輪式機器人系統建模方法逐漸優化，以提高效率和精度。農業機器人在特定環境執行任務過程中，需要在短時間內躲避障礙物，欠驅動控制運動靈活的特點可以高效地解決這個問題。在實際控制過程中，農業輪式機器人驅動部分含有驅動輪和被動輪，機械臂含有主動鉸鏈和被動鉸鏈，為實現農業輪式機器人的精確控制，該類欠驅動系統廣義動力學的建模顯得尤為重要[1]。

目前，動力學建模有多種分析方法，常見的兩種方法是利用力的動態平衡的牛頓-歐拉方程法和拉格朗日功能平衡法即拉格朗日力學法，還有旋量對偶法及凱恩(Kane)方法等。多體系統分析中，常用的牛頓-歐拉方法對多自由度的復雜系統建模效率比較低。Garrera和Serna等人研究了柔性多體系統動力學建模，但其效率是O(N3)，本文利用空間算子代數理論建立了效率為O(n)階廣義動力學模型，擴展性較強。

機器人逆運動學的解法有多種，如Pieper方法、矩陣分解變換法、數值迭代法、Lee和Ziegler的幾何法及代數方法等。實際應用中，機器人建模精度會因強耦合性、非線性等因素而受到影響，傳統的逆運動學算法已經不能滿足高精度作業要求。本文采用Elman神經網絡[2]擬合非線性的反解問題，其特點是在前饋型神經網絡的隱層中增加了承接層，承接層具有延時和儲存的作用，接收隱層神經元的輸出，儲存隱層神經元前一刻的輸出并且反饋給網絡的輸入。這些反饋回路對網絡的學習能力和網絡性能有著重要的影響，使其能夠以任意的精度逼近非線性系統的映射，可以解決操作臂運動學反解問題。

機械臂系統是一個復雜的非線性強耦合系統，對機械臂的精確控制，建模中的矩陣參數的不確定性等都會給控制帶來影響。本文利用RBF神經網絡對動力學模型中的系數矩陣分別逼近、實時反饋并結合PID魯棒理論設計了RBF-PI魯棒-滑模控制，并利用Lyapunov 穩定性理論證明了設計系統的穩定性和收斂性。

為此，本文針對6自由度機械臂農業輪式機器人設計了一種基于RBF神經網絡的農業輪式機器人PI魯棒-滑膜控制，通過反向運動學算法仿真以及對機械臂末端執行器實時軌跡跟蹤控制仿真驗證了該控制算法的合理性。

1 農業輪式機器人總體設計

本文研究對象為AMR果蔬自動收獲機器人，其詳細介紹可參考文獻[4]。機器人由機械臂和輪式移動平臺兩部分組成，輪式移動平臺由前輪轉向部分、后輪驅動部分和車架組成，機械臂自由度選6，整體機械系統結構如圖1所示。

圖1 研究對象結構簡圖

為了滿足田壟間距和果蔬高度的一般要求，設計自動收獲機器人車輪間距和車體高均為500mm，前后4個車輪采用4個獨立伺服電機單獨控制，前輪采用同步帶傳動，后輪采用鏈傳動。采摘機械臂選用6自由度機械臂，機械臂底部通過機械臂安裝臺與車架相連接，轉向采用同步帶傳動，保證了傳動精度和靈活性。機械臂前3個關節確定位置，后3個關節確定姿態，為了控制計算的方便、減少逆解的計算量、避開關節距離偏置，設計機械臂的6個旋轉關節串聯在同一條直線上。底部腰關節、腰關節上部的大臂和小臂長度分別為600、700、400mm。腰關節、大臂和小臂可旋轉角度分別為360°、270°、270°。對于6自由度機械臂來說，運動學逆解非常復雜且一般沒有封閉解。由文獻[3]可知：如果機械手滿足Pieper準則[3]，則封閉解的問題便可以解決，因此設計在小臂上部依次串聯相互垂直的3個旋轉微關節，保證了Pieper準則中3個關節軸線相交于一點的要求，其旋轉角度依次為360°、270°和360°。

2 農業機器人操作臂運動學反解算法

本文采用Elman神經網絡解決機器人逆運動學問題，運動學分析和樣本獲取方法可參考文獻[4]。

Elman神經網絡結構由輸入層、隱層、承接層和輸出層構成，如圖2所示。承接層的存在構成反饋回路，由具有單位延時算子的特殊分支構成，記為Z-1。網絡輸入矩陣P為?,β,γ,px,py,pz，由已知各關節旋轉角度利用機器人正運動學公式計算得出。輸出矩陣Y為q1,q2,q3,q4,q5,q6，根據各關節允許轉動范圍隨機取數并組合在一起。隱層神經元輸出為

(1)

Elman神經網絡的輸出為

(2)

圖2 ELM神經網絡結構示意圖

3 農業機器人廣義動力學模型

根據文獻[4]，利用空間算子代數理論欠驅動農業機器人系統動力學方程和系統的動力學微分-代數方程組可以表述為

(3)

(4)

詳細參數解釋可以參考文獻[5-6]。

4 機器人RBF-PI魯棒-滑模控制設計

4.1 RBF神經網絡逼近算法

RBF神經網絡是局部映射網絡，對輸入的局部空間做出一些神經反饋繼而做出RBF網絡輸出，RBF神經網絡可以通過存在于隱藏層的足夠數量的神經以任意精度逼近任意的單值連續函數。

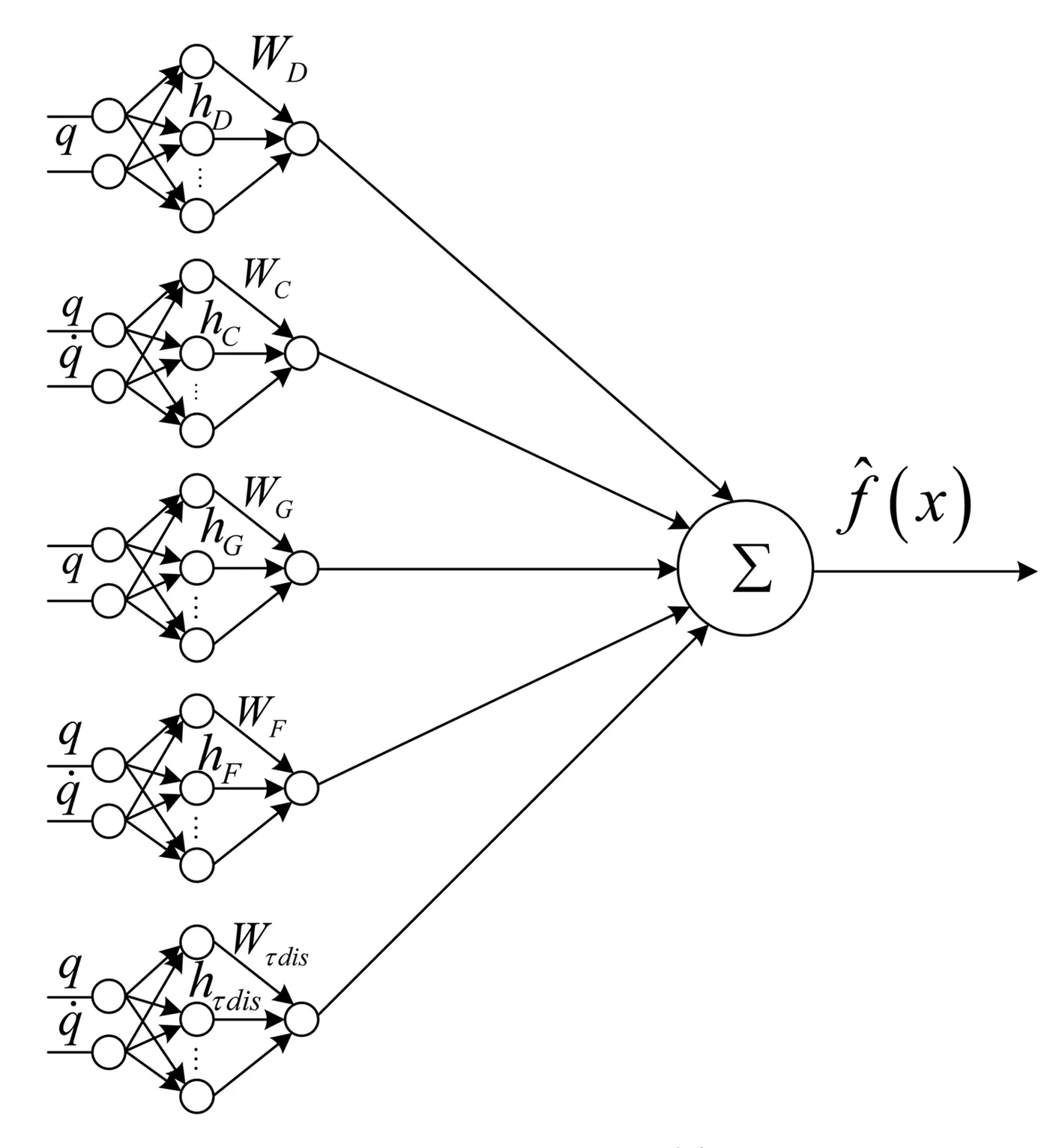
圖3 RBF神經網絡結構示意圖

根據神經網絡的輸出的表達形式，網絡輸入取

x=(q1,q2,q3,q4,q5,q6)

根據文獻[6]中欠驅動農業機器人系統廣義動力學公式，為方便分析，將式(3)簡化成以下二階非線性微分方程，即

(5)

忽略摩擦力矩陣和噪聲，進一步簡化為

(6)

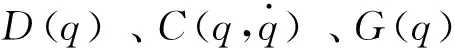
ΔD=Dq-DSNNq

ΔG=Gq-GSNNq

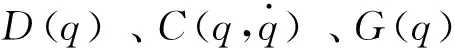
DSNNq=WDT·HDq

GSNNq=WGT·HGq

其中，WD、WC、WG分別為神經網絡隱層到輸出層的連接權值；HDq、HCz、HGq分別為高斯基函數的輸出，則

(7)

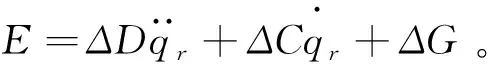
4.2 PI魯棒-SMC控制設計

4.2.1 滑模變結構原理控制分析

根據文獻[7-8]多自由度機械臂的滑模變結構控制公式可以表示為

τs=τg+τl

(8)

其中，τg為動力學系統估計參數，可表示為

(9)

τl可以表示為

τl=ΓssgnS

(10)

代入等式得

τs=τg+ΓssgnS

(11)

由等式(8)～ 式(11)得該機械臂的滑模變結構控制的表達式為

(12)

其中，滑模面S設計為

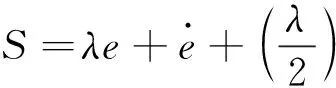
4.2.2 系統控制率設計

本文設計RBF-PI魯棒-滑模控制結構示意圖如圖4所示。設計過程如下：

取qd為指令位置信息，q為實際位置信息，e為位置跟蹤誤差信息。

圖4 六自由度機械臂的構控制示意圖

定義

et=qdt-qt

(13)

(14)

(15)

(16)

(17)

其中，Λ>0。

(18)

(19)

(20)

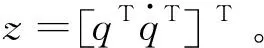
(21)

為提高運動控制精度，本文將PI魯棒控制加入到RBF神經網絡-SMC控制率中。設計τb為

(22)

又

(23)

所以，RBF-PI魯棒-滑模控制控制率設計為

(24)

其中，Kp>0，Ki>0，則

取

τr=Krsgnr

其中，Kr=diagkrii，krii≥Ei。

由

(25)

得

(26)

整理得

(27)

定義自適應律為

(28)

取Lyapunov函數為

V=Vb+Vs

(29)

(30)

其中，ΓDk，ΓCk，ΓGk為正定矩陣，則

(31)

(32)

將式(27)代入式(32)，得

(33)

由于

(34)

同理可知

(35)

(36)

故

(37)

又

(38)

代入自適應律得

(39)

設計Vs部分如下

(40)

則

(41)

(42)

V=Vb+Vs≤0

故本文設計系統是穩定的。

5 仿真分析

5.1 反向運動學仿真

運用第2節中所述方法對農業機器人機械臂逆運動學算法進行仿真試驗，試驗數據準備2 000組，隨機選取100組作為性能檢測數據，其余1 900組為訓練數據。每組數據包括6個輸入矢量和6個輸出矢量，前3個關節的角度誤差曲線如圖5所示。

圖5 機器人前3個關節角度誤差曲線

5.2 控制算法仿真

將滑模變結構控制、PID反饋控制、滑模變結構PID控制分別應用到如圖6所示農業機器人的數學模型中，控制該機器人機械臂末端進行心形軌跡跟蹤。3種控制算法仿真結果如圖7、圖8所示。通過比較可以得出本文采用的控制算法效率較高。

圖6 農業輪式機器人實物圖

圖7 3種機械臂末端軌跡跟蹤控制誤差曲線對比圖

圖8 RBF-PI魯棒-滑模控制機器人末端軌跡

6 結論

1)利用空間算子代數理論建立了機器人O(n)階效率運動學和廣義動力學模型，并運用Elman神經網絡處理運動學反解問題。

2)結合神經網絡控制理論、PID魯棒理論和Lyapunov 穩定性理論設計了農業機器人末端軌跡的RBF-PI魯棒-滑模控制算法，并通過仿真實驗驗證了本設計算法的合理性。

3)找到了一種效率較高的農業機器人機械臂控制方法，提高了實際農業作業過程中的使用效率。控制仿真數據可以作為樣機電機和控制器選型的依據，減少了研發周期，降低了機器人制作成本。