Vine-GAS-Copula模型的統(tǒng)計推斷

(中央民族大學(xué)理學(xué)院 北京 100081)

一、引言

受經(jīng)濟全球化、金融一體化以及人類命運共同體的影響，金融市場之間的相互依賴和相互影響與日俱增，對金融市場之間相關(guān)性的研究已成為現(xiàn)代金融分析的重要內(nèi)容。近年來，由于傳統(tǒng)的金融模型無法滿足金融結(jié)構(gòu)的建模需求，一種研究隨機變量間非線性相關(guān)結(jié)構(gòu)的統(tǒng)計方法——Copula 函數(shù)在經(jīng)濟金融領(lǐng)域得到廣泛應(yīng)用。Copula函數(shù)理論的出現(xiàn)為分析多元金融時間序列提供了一種新的思維模式，與傳統(tǒng)度量相關(guān)性的方法相比，它有以下幾個優(yōu)勢：首先，Copula函數(shù)推導(dǎo)的Spearman相關(guān)系數(shù)ρ和Kendall相關(guān)系數(shù)τ等在嚴(yán)格單調(diào)遞增的情況下保持不變，即在變量存在非線性相關(guān)的條件下，該相關(guān)性指標(biāo)也可以應(yīng)用。其次，Copula函數(shù)可以把分布不同的邊緣分布函數(shù)連接起來構(gòu)造聯(lián)合分布函數(shù)，在實際應(yīng)用時，我們可以分開討論變量的邊緣分布和變量間的相關(guān)性，從而Copula函數(shù)可以與時間序列模型獨立的結(jié)合，故相比其他金融模型運用更靈活。最后，Copula函數(shù)可以有效處理尾部相關(guān)問題。Copula理論對金融時間序列的建模多局限于二維的情況下，對于高維情況的使用也僅限于多元高斯Copula函數(shù)和多元t-copula函數(shù)。而這兩種copula函數(shù)都需假定多元金融時間序列的邊緣分布均為正態(tài)分布或t分布，因此不能很好地估計序列間的相依結(jié)構(gòu)。Bedford和Cooke(2002)首次采用圖形建模工具中“藤”的層疊結(jié)構(gòu)，將高維Copula函數(shù)分解為一系列Pair-Copula函數(shù)，更好的描述了多元金融時間序列間的相依結(jié)構(gòu)。

在實際中，隨著科技發(fā)展的日新月異，金融市場會根據(jù)外部市場環(huán)境的瞬息萬變與國家宏觀經(jīng)濟政策的調(diào)整而改變，因而金融市場之間的相關(guān)關(guān)系會隨著時間的推移而發(fā)生變化，即金融市場之間的相關(guān)性具有顯著的時變特征。時變相關(guān)的Copula模型，其Copula模型的形式是不變的，但模型中的參數(shù)是隨時間變化的。構(gòu)建這種模型關(guān)鍵在于要給出Copula函數(shù)的相關(guān)參數(shù)的演化方程，由于許多Copula函數(shù)的參數(shù)與相關(guān)性度量或尾部相關(guān)系數(shù)有一一對應(yīng)的關(guān)系，因此要構(gòu)建時變相關(guān)的Copula模型，我們可以通過確立Copula函數(shù)相關(guān)性度量的演化過程來建立其參數(shù)的演化方程。在時變 Copula 函數(shù)的理論研究方面，已有文獻主要集中于二維時變 Copula 的建模研究，主要是假設(shè)Copula函數(shù)的參數(shù)是時間的某個確定函數(shù)，進而對時變參數(shù)進行建模，例如Patton(2006)提出二維Copula函數(shù)的當(dāng)前相關(guān)性可以通過歷史相關(guān)性和兩個變量累積概率的歷史平均值來解釋。此外，也有學(xué)者認(rèn)為Copula函數(shù)的參數(shù)是時間的未知函數(shù)，可以通過非參數(shù)估計的方法對時變參數(shù)進行建模，例如龔金國和史代敏提出用經(jīng)驗分布函數(shù)-局部極大似然法(ECDF-LML)來估計Copula函數(shù)中的時變參數(shù)。本文主要借鑒Creal等提出的廣義自回歸得分(GAS)模型的思想，即用似然函數(shù)的比例分?jǐn)?shù)來更新時變參數(shù)，以此建立參數(shù)的時變過程。該理論是一種數(shù)據(jù)驅(qū)動時變參數(shù)的理論建模方法，其為非線性時間序列模型引入時變參數(shù)提供了統(tǒng)一框架。

二、基于GAS理論的時變Vine-Copula模型

由Sklar定理可知：設(shè)F(·)為隨機向量X=(X1,X2,…,Xn)∈Rn的聯(lián)合分布函數(shù)，F(xiàn)i(·)是隨機變量Xi的邊緣分布函數(shù)，i=1,…,n，則存在一個Copula函數(shù)C(·)，滿足：

F(x1,…,xn)=C(F1(x1),…,Fn(xn))

當(dāng)且僅當(dāng)Fi(·)，i=1,…,n連續(xù)時，Copula函數(shù)唯一確定。

(一)Vine-Copula模型

對于n維隨機向量的聯(lián)合分布，由于不同的分解形式會有不同的Pair-Copula結(jié)構(gòu)，為了使選擇的Pair-Copula結(jié)構(gòu)更符合邏輯，Bedford和Cooke(2001，2002)引入了一種圖形建模工具——正則藤(R-vine)，包含節(jié)點、邊和樹結(jié)構(gòu)。常用的R-vine包括C-vine和D-vine。對于Vine結(jié)構(gòu)的選擇，可以通過計算變量之間的Kendall秩相關(guān)系數(shù)來確定使用C-Vine建模還是使用D-Vine建模，也可以通過對比建立Vine結(jié)構(gòu)之后模型的AIC值來確定模型最終采用的Vine結(jié)構(gòu)。

C-Vine中，每棵樹有唯一的節(jié)點連接其他節(jié)點，即主節(jié)點之外的其他節(jié)點僅連接一條邊。對于n維隨機向量X=(X1,X2,…,Xn)，若變量Xi與其他變量的相關(guān)性顯著大，即存在關(guān)鍵變量Xi能引導(dǎo)其他變量，此時用C-Vine建模較為合適。

n維隨機向量X的C-Vine結(jié)構(gòu)的聯(lián)合密度函數(shù)為：

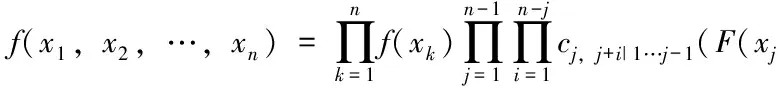
圖1 4維情況下的C-vine Copula結(jié)構(gòu)分解圖

圖1展示的是在4維情況下的C-Vine Copula的結(jié)構(gòu)分解圖，可以看出，它包含3棵樹Tj,j=1,2,3，每棵樹Tj有5-j個節(jié)點和4-j條邊，每條邊都對應(yīng)一個Pair-Copula函數(shù)。圖1對應(yīng)的聯(lián)合密度函數(shù)可分解為：

f(x1,x2,x3,x4)=f1(x1)*f2(x2)*f3(x3)*f4(x4)*c12(F1(x1),

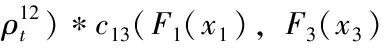
其中：

D-Vine中，每棵樹的任意節(jié)點最多連接兩條邊。對于n維隨機向量X=(X1,X2,…,Xn)，若變量之間的相關(guān)性相差不大，即變量之間相對獨立，此時用D-Vine建模較為合適。

n維隨機向量X的D-Vine結(jié)構(gòu)的聯(lián)合密度函數(shù)為：

F(xj+i|xi+1,…,xi+j-1)

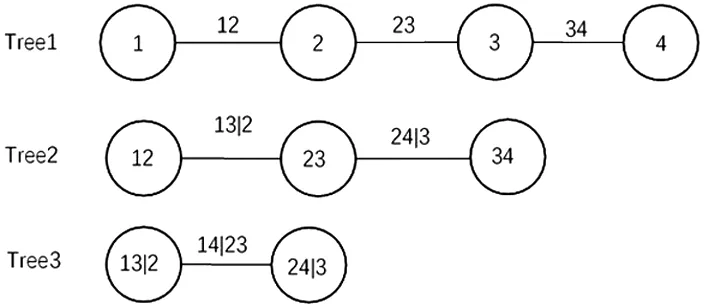
圖2 4維情況下的D-vine Copula結(jié)構(gòu)分解圖

圖2展示的是在4維情況下的D-Vine Copula的結(jié)構(gòu)分解圖，與C-Vine Copula類似，它也包含3棵樹Tj,j=1,2,3，每棵樹Tj有5-j個節(jié)點和4-j條邊，每條邊都對應(yīng)一個Pair-Copula函數(shù)。圖2對應(yīng)的聯(lián)合密度函數(shù)可分解為：

f(x1,x2,x3,x4)=f1(x1)*f2(x2)*f3(x3)*f4(x4)*c12(F1(x1),

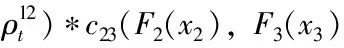
(二)Vine-GAS-Copula模型

本文主要借鑒Creal等提出的廣義自回歸得分(GAS)模型的思想，即用似然函數(shù)的比例分?jǐn)?shù)來更新時變參數(shù)，以此建立參數(shù)的時變過程。該理論是一種數(shù)據(jù)驅(qū)動時變參數(shù)的理論建模方法，其為非線性時間序列模型引入時變參數(shù)提供了統(tǒng)一框架。

二元Copula GAS(p,q)時變參數(shù)的演變模式如下：

其中，αt為Copula函數(shù)在t時刻的參數(shù)向量，Λ(·)為修正的logistic轉(zhuǎn)換函數(shù)，以保證參數(shù)取值落入所屬Copula函數(shù)參數(shù)的定義域內(nèi)；ω為截距向量，Ai、Bj為系數(shù)矩陣，i=1,…,p;j=1,…,q；c(·)為Copula函數(shù)的密度函數(shù)，t是得分向量，即Copula對數(shù)似然函數(shù)關(guān)于參數(shù)ft的導(dǎo)數(shù)；St是比例矩陣，這里定義為Copula對數(shù)似然函數(shù)關(guān)于參數(shù)ft的信息矩陣的逆。

對于n維C-Vine Copula的聯(lián)合密度函數(shù)，有

f(y1,y2,…,yn)=c(F1(y1),…,Fn(yn);θ)·f1(y1)·…·fn(yn)

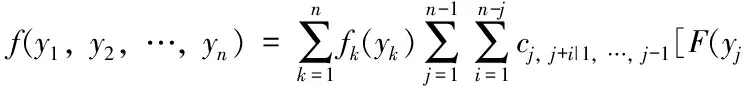
因此，可以得到其對數(shù)似然函數(shù)：

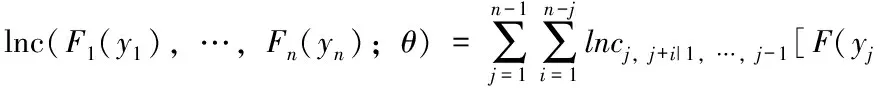
F(yj+i│Ij-1);θj,j+i]

將上式對參數(shù)θ(j,j+i)求導(dǎo)，有：

由上式可以得出，求解n維C-Vine Copula聯(lián)合密度函數(shù)的參數(shù)θj,j+i可以等價于求解對應(yīng)Pair-Copula密度函數(shù)的參數(shù)，即關(guān)于時變θj,j+i的信息可以從包含它的Pair-Copula的似然函數(shù)中得到。綜上我們可以得到基于GAS理論的時變C-Vine Copula模型，記為C-Vine-GAS-Copula模型，D-Vine-GAS-Copula模型類似。

(三)Vine-GAS-Copula模型的估計

三、實證分析

本文選取2013.5-2019.6富時指數(shù)、上證指數(shù)、深證指數(shù)、道瓊斯指數(shù)的日收盤價作為研究對象，并采用對數(shù)收益進行分析：

rt=lnpt-lnpt-1

(一)統(tǒng)計檢驗

1.描述性統(tǒng)計

對數(shù)收益序列的主要統(tǒng)計特征及直方圖如下所示：

富時上證深證道瓊斯Minimum-9.74363-8.87291-8.60356-9.1253Maximum6.8266515.6036126.2541886.071573Mean0.031520.017189-0.001410.024232Median0.0034620.065040.0360730.071682Variance2.4303272.1469842.9847652.361412Stdev1.558951.4652591.7276471.536689Skewness-0.52817-1.12059-0.84607-1.05486Kurtosis5.4822336.7822054.1217916.381867J-B檢驗1941.793177.151236.9452813.544(p-Value)<2.2e-16<2.2e-16<2.2e-16<2.2e-16

圖3對數(shù)收益序列的直方圖

四個序列偏度均小于0，分布均有長的左拖尾。峰度均高于正態(tài)分布峰值3，說明具有尖峰厚尾的特征。同時J-B統(tǒng)計量均拒絕服從正態(tài)分布假設(shè)。

2.時序圖

圖4 對數(shù)收益序列的時序圖

四個對數(shù)收益序列的時序圖均存在波動聚集性，即四個序列均可觀察到波動的“集群”現(xiàn)象，波動在一段時間內(nèi)較小，在有的時間段內(nèi)非常大。

3.ADF檢驗和L-B檢驗

表2 ADF檢驗

表3 Ljung-Box檢驗

四個序列均通過ADF檢驗和L-B檢驗，即序列均為平穩(wěn)非白噪聲序列，可以進行ARIMA建模。

4.ARCH效應(yīng)檢驗

根據(jù)AIC信息準(zhǔn)則確定序列擬合的最優(yōu)ARMA模型均是ARMA(3,2)，對殘差序列進行ARCH效應(yīng)檢驗：

表4 ARCH LM檢驗

所有序列的殘差都存在 ARCH 效應(yīng)。故可以建立 GARCH 類模型擬合邊緣分布。

(二)邊際分布的確定

根據(jù)AIC信息準(zhǔn)則確定序列擬合的最優(yōu)ARMA-GARCH模型分別為：

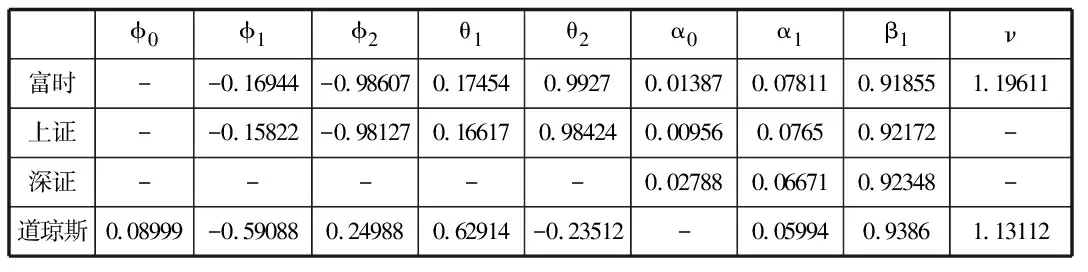
表5 最優(yōu)ARMA-GARCH模型

對建模后的標(biāo)準(zhǔn)殘差序列進行ARCH效應(yīng)檢驗，結(jié)果拒絕ARCH效應(yīng)，表明標(biāo)準(zhǔn)殘差序列已無二階相關(guān)性，GARCH建模效果良好。

(三)Vine-GAS-Copula模型的建立

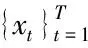
xt=μxt+εxt

εxt=σxtξxt

yt=μyt+εyt

εyt=σytξyt

(ξxt,ξyt)～Cξt(F(ξxt),F(ξyt))

運用Copula模型建立金融時間序列模型，可將研究收益序列之間的條件相關(guān)性簡化為研究殘差序列之間的相關(guān)性。

1.概率積分變換

對標(biāo)準(zhǔn)化殘差進行概率積分變換，K-S檢驗變化后的序列服從[0,1]上的均勻分布，故可以用來構(gòu)建 Copula 函數(shù)。

表6 K-S檢驗

本文采用CML方法估計Copula函數(shù)的參數(shù)，先用經(jīng)驗分布函數(shù)將原始數(shù)據(jù)(xt,yt)轉(zhuǎn)換為均勻分布變量序列(ut,vt)，然后用極大似然估計對Copula函數(shù)進行參數(shù)估計：

2.Vine-GAS-Copula模型

根據(jù)標(biāo)準(zhǔn)化殘差之間的關(guān)系，本文采用二元時變高斯Copula來描述序列間的相關(guān)關(guān)系，其時變參數(shù)的演變模式為：

其中xt=[Φ-1(ut)]2+[Φ-1(vt)]2，yt=Φ-1(ut)Φ-1(vt)。

根據(jù)標(biāo)準(zhǔn)化殘差之間的相關(guān)性(表7)，道瓊斯指數(shù)序列的標(biāo)準(zhǔn)化殘差(V4)與其他變量關(guān)系更為密切，符合C-Vine結(jié)構(gòu)特征，應(yīng)以V4為主節(jié)點對第一層進行建模，同樣，根據(jù)表8可以發(fā)現(xiàn)富時|道瓊斯(V1|4)與其他變量關(guān)系更密切，應(yīng)以V1|4為主節(jié)點對第二層進行建模。綜上所述，得到C-Vine Copula結(jié)構(gòu)分解圖：

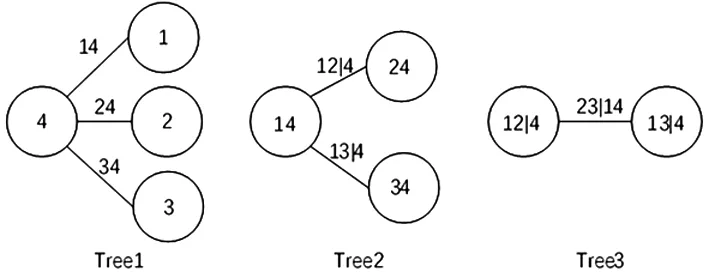
圖6 C-VineCopula結(jié)構(gòu)分解圖

表7 樹1的Kendall秩相關(guān)系數(shù)

表8 樹2的Kendall秩相關(guān)系數(shù)

3.求解時變參數(shù)方法對比

采用AIC準(zhǔn)則法對比求解時變參數(shù)的三種方法，由下表可以看出，把時變參數(shù)當(dāng)做常數(shù)求值時，參數(shù)值相對穩(wěn)定，其AIC值最大；用patton法求解時變參數(shù)時，參數(shù)值隨時間的變化明顯，其AIC值略小；用GAS法求解時變參數(shù)時，參數(shù)值隨時間的變化更明顯，其AIC值最小。

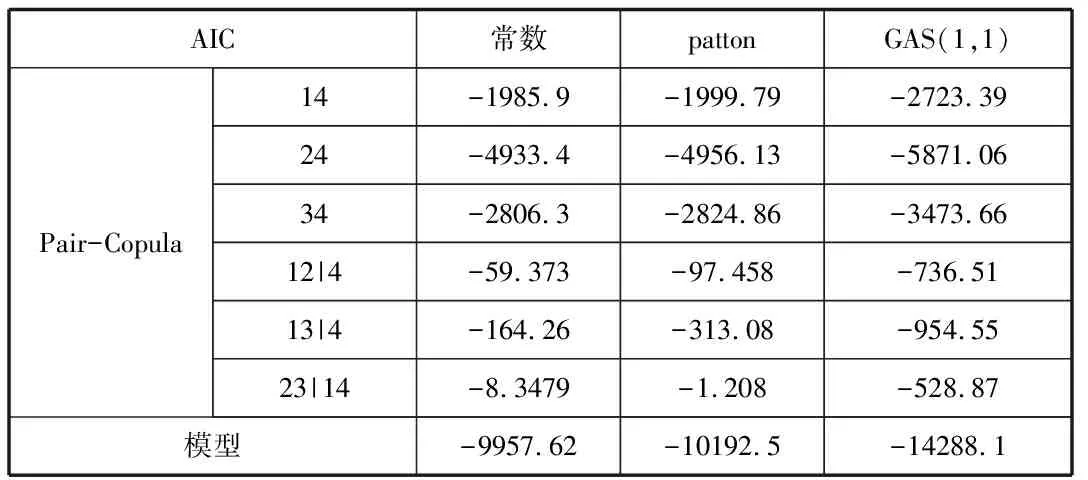
表9 不同時變參數(shù)的AIC值

四、研究結(jié)論

本文基于Vine-Copula結(jié)構(gòu)與廣義自回歸得分(GAS)理論提出了Vine-GAS-Copula模型，對多元金融時間序列間的相依結(jié)構(gòu)進行建模。實證結(jié)果表明，相比較于常值參數(shù)Copula模型與patton時變參數(shù)Copula模型，Vine-GAS-Copula模型對數(shù)據(jù)相關(guān)結(jié)構(gòu)的擬合程度更好，這在一定程度上表明Vine-GAS-Copula模型可以很好地擬合時變的多元金融時間序列。