三角形中的一條線、兩個模型、三個結論

江蘇省南通田家炳中學 潘丹丹

三角形是人教版八年級上冊第十一章內容，如何研究與三角形相關的角是研究的重點與難點，通過對與三角形有關內容的分析與認識，筆者對如何求與三角形相關的角及與三角形相關的角的一些題型做了適當的認識與總結，如有不當之處，敬請批評指正.

一、三角形中的一條線——內角和定理或外角結論

與三角形有關的角包括內角和外角，如何去求相關角呢？筆者認為，牢牢抓住內角和定理或者外角結論，在求與三角形相關的角時，首先確定所研究的角是什么角，抓住三角形的內角和定理（三角形三個內角和等于180°）這條線，或者抓住外角結論（三角形的外角等于與它不相鄰的兩個內角的和）這條線.

基于三角形求角中一條線的思路認識，可進一步得出以下兩個模型及對三個結論的認識.

二、兩個模型——飛鏢模型和8字模型

1.8字模型

如圖1，試探究∠A、∠B、∠C、∠D的關系.

結論：∠A+∠B=∠C+∠D.

通過對三角形中研究角時一條線的認識，可知應緊抓三角形的內角和定理.證明如下：

證明：在△ABE中，∠A+∠B+∠AEB=180°，所以∠A+∠B=180°-∠AEB.

在△CDE中，∠C+∠D+∠CED=180°，所以∠C+∠D=180°-∠CED.

又因為∠AEB=∠CED，所以∠A+∠B=∠C+∠D.

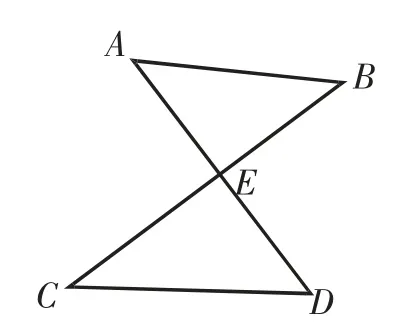
圖1

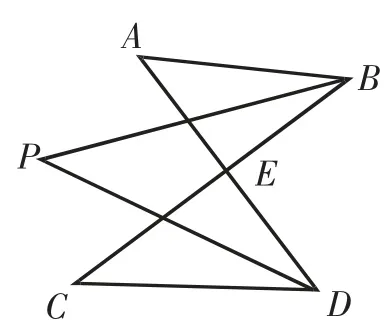
圖2

建立在8字模型的基礎上，將8字模型與角平分線結合，有如下問題探究：

如圖2，BP、DP分別平分∠B、∠D，相交于點P，試探究∠P與∠A、∠C的關系.

證明：記線段AD、BP相交于點M，則根據8字模型結論得∠A+∠ABP=∠P+∠ADP ①.

記線段BC、DP相交于點N，則根據8字模型結論得∠P+∠CBP=∠C+∠CDP ②.

因為BP、CP分別平分∠ABC、∠ADC，所以∠ABP=∠CBP，∠ADP=∠CDP.

認識了8字模型與角平分線的結合，在此基礎上還可做如下變式：

證明：記線段AD、BP相交于點M，則根據8字模型結論得，所以∠ABC-∠ADC=3（∠P-∠A）.

記線段BC、DP相交于點N，則根據8字模型結論得∠P+∠CBP=∠C+∠CDP，則，所以

進一步可以推廣到一般情況：

2.飛鏢模型

如圖3，試探究∠A、∠B、∠C、∠D的關系.

結論：∠D=∠A+∠B+∠C.

通過對三角形中研究角時一條線的認識，有以下思考：

證法1：（利用三角形內角和定理）連接BC.

在△ABC中，∠A+∠ABC+∠ACB=180°，所以∠A+∠ABD+∠ACD=180°-∠DBC-∠DCB.

在△DBC 中，∠BDC+∠DBC+∠DCB=180°，則∠BDC=180°-∠DBC-∠DCB，所以∠BDC=∠A+∠ABD+∠ACD.

證法2：（構造外角，利用外角結論）連接AD并延長至點E.

根據外角結論，得∠BDE=∠B+∠BAE，∠CDE=∠C+∠CAD，所以∠BDE+∠CDE=∠B+∠C+∠BAE+∠CAD，即∠BDC=∠BAC+∠B+∠C.

實際上在利用外角結論證明時，也可用以下方法：延長線段BD交AC于點M，或者延長線段CD交AB于點N.

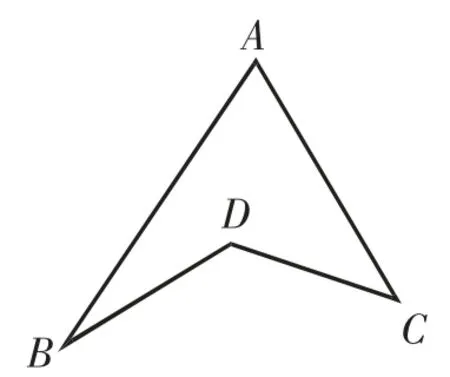
圖3

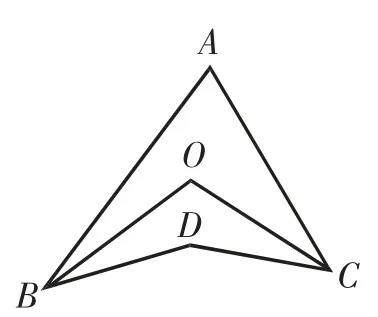
圖4

建立在飛鏢模型的基礎上，將飛鏢模型與角平分線結合，有如下問題探究：

如圖4，BO、CO分別平分∠ABC、∠ACB，相交于點O，試探究∠A、∠O、∠D的關系.

結論：∠A+∠D=2∠O

證明：由飛鏢模型可得：∠O=∠A+∠ABO+∠ACO，∠D=∠O+∠OBD+∠OCD.

因為BO、CO分別平分∠ABC、∠ACB，所以∠ABO=∠OBD，∠ACO=∠OCD.則∠O-∠A=∠D-∠O，故∠A+∠D=2∠O.

認識了飛鏢模型與角平分線的結合，在此基礎上還可做如下變式：

證明：由飛鏢模型可得：∠O=∠A+∠ABO+∠ACO，∠D=∠O+∠OBD+∠OCD.

進一步可以推廣到一般情況：

將8字模型、飛鏢模型與對角線結合得到了一般性的結論，而三角形中角平分線的一般結論又如何呢？

三、三個結論（三角形中角平分線的結論）

1.兩個內角平分線的結論

在△ABC中，∠ABC的平分線和∠ACB的平分線交于點P，如圖5，試猜想∠P與∠A的關系，并予以證明.

證明：在△PBC中，∠P=180°-∠PBC-∠PCB.

因為BP、CP分別平分∠ABC、∠ACB，所以∠PBC=

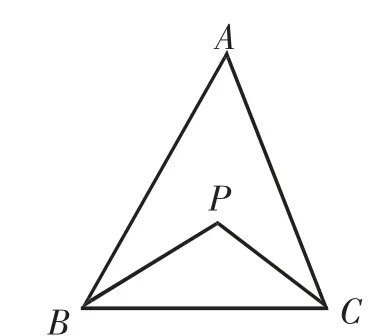
圖5

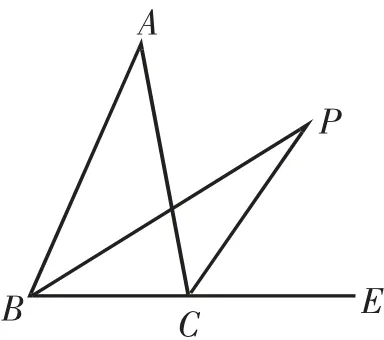
圖6

2.一個外角與一個內角平分線的結論

在△ABC中，一個外角∠ACE的平分線和一個內角∠ABC的平分線交于點P，如圖6，試猜想∠P與∠A的關系，并予以證明.

證明：因為∠PCE為△PBC的外角，所以∠P=∠PCE-∠PBC.

因為BP、CP分別平分∠ABC、∠ACE，所以∠PBC=

3.兩個外角平分線的結論

在△ABC 中，兩個外角∠EBC的平分線和∠FCB的平分線交于點P，如圖7，試猜想∠P與∠A的關系，并予以證明.

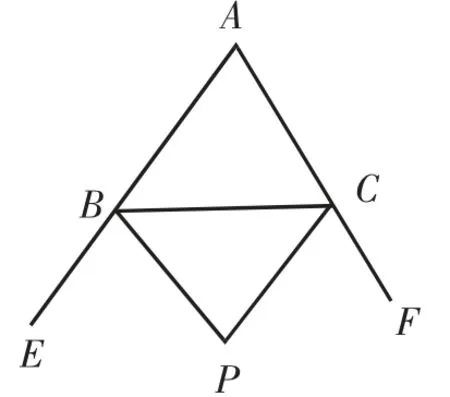
圖7

證明：在△PBC中，∠P=180°-∠PBC-∠PCB.

因為BP、CP分別平分∠EBC、∠FCB，所以∠PBC=

建立在三角形中角平分線的結論上，與之方法類似，以上問題均可拓展到一般情況并得到一般性的結論：

以上內容是對三角形中如何求角這個問題的部分認識，充分掌握好以上問題的結論及證明過程，在適當情況下能起到事半功倍的作用.實際上，不管是三角形中求什么角的問題，核心本質都是首先抓住這個角是什么角，然后充分利用內角和定理或者外角結論進行轉化解決.