商業建筑火災初期風險模糊系統分析
閆金花 (西南科技大學土木工程與建筑學院,四川 綿陽 621010)
0 前言
商業建筑是許多重特大火災事故頻發的場所,存在諸多火險隱患、火災初期階段是控制火災進一步蔓延,防止重特大火災事故發生的關鍵時期,也是人員疏散的最佳時段。由于初期階段滅火因素比較復雜,有建筑自身存在的消防隱患,也有人為造成的失誤,要在很短的時間內滅火成功,存在一定難度。本文首先構建了商業建筑火災初期風險模糊系統模型,并給出了各基本事件的隸屬函數,通過建立模糊系統模型的結構函數,確定出商業建筑火災初期風險模糊系統的模糊數,最后通過模糊重要度分析,給出減少商業建筑火災初期風險的對策。
1 火災初期模糊系統模型
通過調查我國商業建筑重特大火災案例,分析在火災的初期階段火險隱患,確定出目標事件、中間事件、基本事件,建立商業建筑火災初期風險模糊系統模型,見圖1。模型中各基本事件分別用:ai,i=1,…,6;bj,j=1,…,6;ck,k=1,2,3;ml,l=1,…,13 表示。
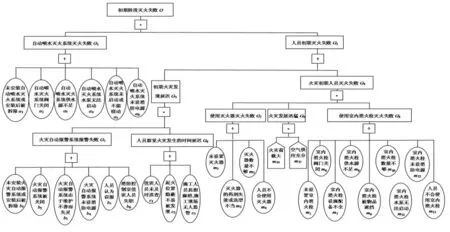
圖1 商業建筑火災初期風險模糊系統模型
2 基本事件隸屬函數的確定
由于各基本事件的概率是在介于[0,1]之間的某一值附近左右波動,因此選用中間型的模糊分布作為基本事件概率的隸屬函數。由于無法判定基本事件概率模糊數中隸屬度為0的點。因此,選用非線性的模糊分布較為合適,于是選取[0,1]區間上的對稱L-R的型模糊數的分布函數,作為模糊故障樹中基本事件概率的隸屬函數,將概率均值的隸屬度取為1。
設目標事件為火災初期滅火失敗事件,用“O”來表示,則各基本事件發生的概率分別為模糊數=(mi,αi,βi),i=1,…,6=(mj,αj,βj),j=1,…,6,=(mk,αk,βk),k=1,2,3=(ml,αl,βl),l=1,…,13,其中 mi、mj、mk、ml分別為各基本事件概率的最大似然估計量。假定 x 當偏離其中心值 50%時,μ≤0.1,則 αi=βi=0.0556mi,i=1,… ,6;αj=βj=0.0556mj,j=1,…,6;αk=βk=0.0556mk,k=1,2,3;αl=βl=0.0556ml,l=1,…,13,那么各基本事件概率模糊數的隸屬函數分別為:
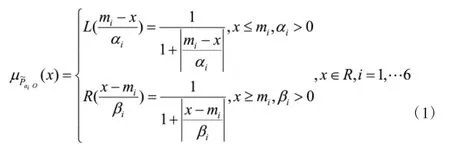

3 模糊系統分析
3.1 系統模糊數
根據系統模型(圖1)得到商業建筑火災初期風險模糊系統的結構函數為:
T=G1·G2=G1·(G3+G4)=G1·(G5·G6+G7+G8)
式中:G1=a1+a2+a3+a4+a5+a6,其中 a1與 a2,…,a6互斥,a2,…,a6之間相互獨立;G5=b1+b2+b3+b4+b5+b6,其中 b1與 b2,…,b6互斥,之間相互獨立;G6=c1+c2+c3,其中 c1,c2,c3之間相互獨立;G7=m1+m2+m3+m4,其中 m1與m2,m3,m4互斥 m2,m3,m4之間相互獨立;G8=m5+m6+…+m13,其中 m5與m6,…,m13互斥,m6,…,m13之間相互獨立。
商業建筑火災初期風險模糊系統頂事件概率為模糊數:
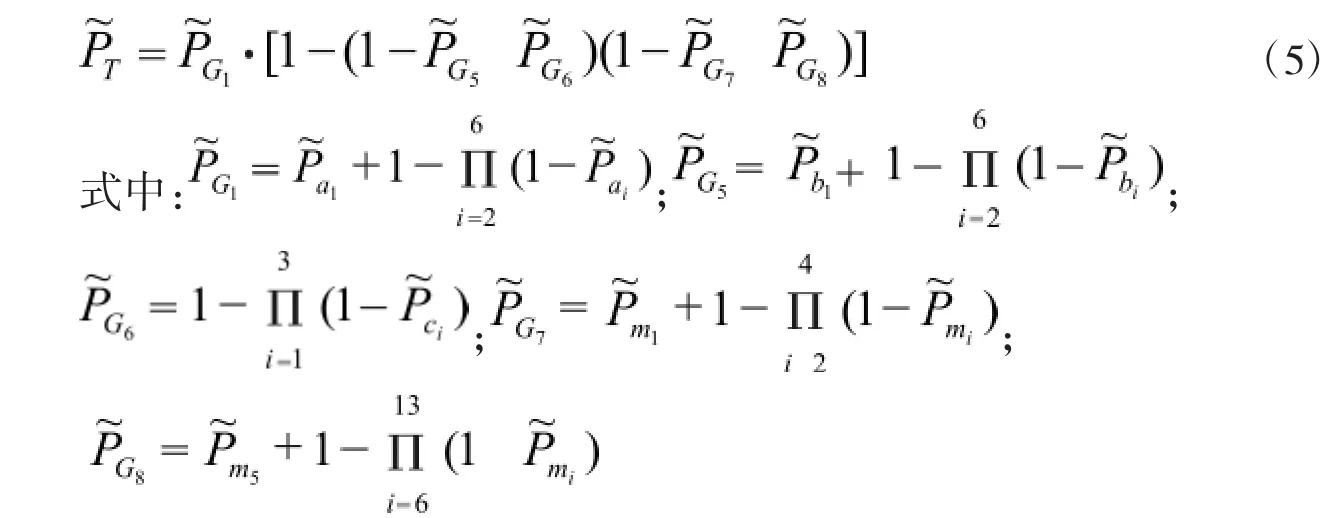
3.2 模糊重要度分析
對于有界模糊數,可以利用模糊數的中值來計算模糊重要度。
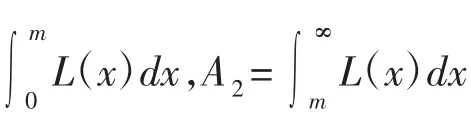
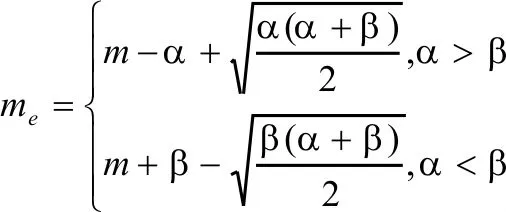
根據定義1和定義2,設火災初期商業建筑火災風險模糊系統的結構函數為 Ψ(X)=Ψ(x1,x2,…,xn),xi故障概率為有界模糊數,其中位數為mTe,模糊系統頂事件概率的可能性分布則為:
仍為有界模糊數,其中值為mTe。
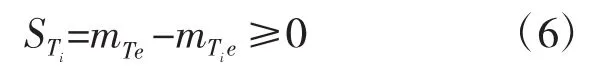
3.3 模型分析
選取50例發生在我國商業建筑特大火災案例進行分析。通過案例統計調查分析,由公式(1)~(4),得到商業建筑火災初期風險模糊系統各基本事件發生的概率,分別為模糊數,i=1,…,6,j=1,…,6,k=1,2,3;,l=1,…,13,見表 1。
再由公式(5)得到商業建筑火災初期風險模糊系統頂事件發生的概率為模糊數:
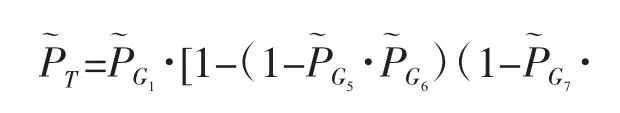
表1 模糊數
其中值為me2=0.504405。
根據公式(6)、(7),得到商業建筑火災初期風險模糊系統各基本事件的模糊重要度,分別為STai,i=1,…,6;STbj,j=1,…,6;STck,k=1,2,3;STml,l=1,…,13,見表2。
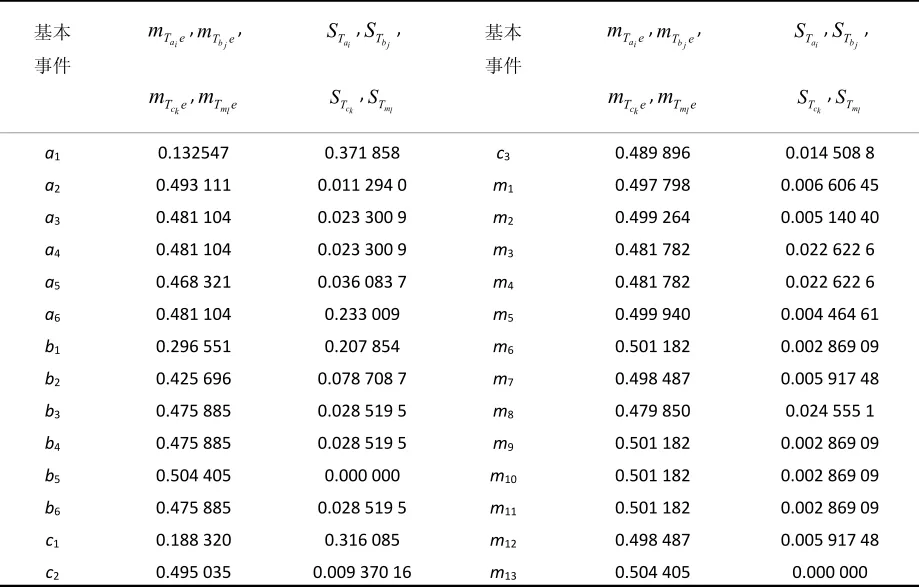
表2 基本事件的模糊重要度
4 結論
①a1事件——未安裝自動噴水滅火系統或安裝后被拆除,c1事件——值班人員未及時巡查,b1事件——未安裝火災自動報警系統或安裝后被拆除,這三個基本事件對初期滅火影響最大,其重要度影響的數量級為10-1,是降低初期火災風險首要解決的關鍵問題。
②火災自動報警系統故障中的b2事件——火災自動報警系統被關閉,對初期滅火影響最大。
③自動噴水滅火系統故障中的a5事件——自動噴水滅火系統未啟動或不能聯動對初期滅火影響最大。
④使用室內消火栓不當,其主要原因是m8事件——室內消火栓供水源不足,其重要度影響的數量級為 10-2。
⑤使用滅火器滅火失敗的m3事件——滅火器數量不夠,m4事件——人員不會使用滅火器,對火災初期滅火影響最大,其重要度影響的數量級為10-2。
⑥c3事件——施工人員思想麻痹,施工現場無人監管,對消除初期火災隱患的影響不可忽視,其重要度影響的數量級為10-2。

