n次單位方根的教學思考

周潘 岳岳成雪 何婧

【摘要】本文給出了高等代數教材中一道課后習題的詳細解答，結合教學經驗提出本題的講解技巧和方法，從而加深學生對該題的理解，幫助學生鞏固相關知識.

【關鍵詞】n次單位方根;教學思考;因式分解

【基金項目】湖南省普通高校教學改革研究項目（湘教通[2018]436號）.

一、問題的提出

北京大學數學系編的高等代數第四版第一章課后習題第26題：將多項式xn-1在復數范圍內和實數范圍內因式分解.下面是眾多參考書中的解答方法.

對上述的解答過程，很多學生表示看不太懂，有的學生表示即使看懂了也不明白該如何去思考這類問題，無法做到觸類旁通.學生之所以存在這樣的問題，往往是由于對知識點的理解不夠透徹.本題涉及的知識點很多，比如，代數基本定理，實數域和復數域上的因式分解唯一性定理，重根的性質，不可約多項式的定義等等.這是一道綜合題，對學生而言，不僅要知道該題所涉及的數學知識點有哪些，還要知道這些知識點在該類問題中是如何應用的.特別是對部分省市的學生，他們的高中數學內容并沒有涉及復數的有關知識或是作為選修課的內容進行教學，學生對復數知識點的掌握較為模糊，因此，在求解本題時往往陷入瓶頸.作為任課教師應考慮如何講解本題，做到既能讓學生知其然而又知其所以然，與此同時，由于課堂時間有限，又不能將本題涉及的所有知識點都一一講解.基于此，本文將探索作為任課教師如何利用有限的課堂時間對本題進行講解，同時讓不同學習背景的學生都能明白和理解本題及相關知識.

二、解答的詳細剖析

（一）復數的預備知識

針對有些學生沒有學習過復數相關知識的情況，教學中，教師首先要對復數的基本概念等相關內容做一些補充.

形如a+bi的數叫作復數，其中a，b是實數，i2=-1.復數通常用字母z表示，即z=a+bi，（a，b∈R），這一表示形式稱為復數的代數形式，a與b分別叫作復數z的實部與虛部.稱a2+b2為復數z=a+bi的模或長度，記為|Z|.當兩個復數的實部相同，虛部互為相反數時，這兩個復數互為共軛復數.

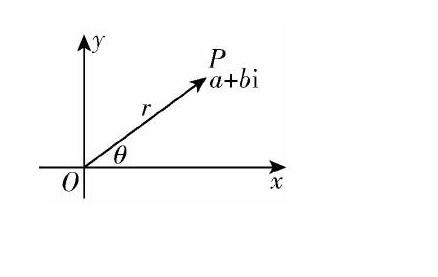
從復數相等的定義知道，任何一個復數z=a+bi都可以由一個有序實數對（a，b）唯一確定.而有序實數對（a，b）與平面直角坐標系中的點一一對應，因此，復數集與平面直角坐標系中的點集之間可以構建一一對應.于是復數z=a+bi可以看作向量OP，如圖所示.向量OP可以由其大小和方向決定：OP的大小為|OP|=r=a2+b2，其方向為OP的傾斜角θ.

（二）因式分解的知識

由因式分解唯一性定理可知，次數大于等于1的多項式，在實數域上能唯一分解成一些一次因式和二次不可約因式的乘積.在復數域上能唯一分解成一些一次因式的乘積.

由一次因式與根的關系，只需要找出xn-1在復數域上的所有根就能知道該多項式在復數域上的因式分解，而在實數域上的因式分解只需要對其實根進行討論.換句話說，在復數域和實數域上的因式分解，最終都轉化為對其根進行研究.

三、教學反思

本題為考研常考類型題，該類題目涉及知識點多，解題過程復雜，課堂上沒有足夠的時間進行詳細講解.大多授課教師在實際授課中往往要求學生直接記住n次單位根，或是只給出解題思路方法，更有甚者選擇不講而讓學生課后找資料自行消化.然而，很多學生沒有能力獨自解決問題，或是知難而棄，同時也大大降低學生的學習積極性，導致大部分學生沒有學到應掌握的知識.針對這一情況，授課教師可以采用微課的教學手段，將該題的講解過程錄制成微課視頻提供給學生，讓學生利用課余時間觀看，再利用課堂時間對學生觀看講解視頻后提出的問題有針對性地進行解答.如此，既節省了課堂時間，又能保證學生對該題充分理解，同時又照顧到了不同學習背景的學生，由此達到教育要促進全體學生共同發展的理念.

【參考文獻】

[1]沈文選.1的n次單位根的性質及應用[J].中學教研，1993（9）：31-35.

[2]北京大學數學系.高等代數：第4版[M].北京：高等教育出版社，2013.

[3]王萼芳，石生明.高等代數輔導與習題解答[M].北京：高等教育出版社，2013.

[4]徐仲.高等代數導教·導學·導考[M].西安：西北工業大學出版社，2014.

[5]中學數學課程教材研究開發中心.高中數學·選修2-2[M].北京：人民教育出版社，2005.