建立平面直角坐標系，定量分析中考幾何壓軸題

黃寶玉

【摘要】近年來，各地不少中考幾何壓軸題，用傳統方法進行定性分析，在有限時間內完成的難度很大，如果能有意識地通過建立平面直角坐標系進行分析、解答，往往更加簡捷、巧妙.本文以2017年廣州中考的一道幾何壓軸題為例，進行對比說明.

【關鍵詞】平面直角坐標系;幾何壓軸題;定量分析

一直以來，圍繞相似三角形、圓等內容命制的純幾何證明題，不斷出現在各地的中考壓軸題中.由于其常需添加輔助線、涉及的數學思想方法眾多、覆蓋的知識面廣，因此，學生在有限的時間內，用傳統幾何方法定性分析，完成的難度很大.縱觀歷年中考試題，不少幾何壓軸題如能有意識地建立平面直角坐標系進行定量分析，往往能收到意想不到的效果，筆者現以廣州市2017年中考數學第25題為例，簡述該題的幾何解題思路，并呈現建立坐標系定量運算的解題思路，凸顯用建立坐標系法解決某些幾何壓軸題的優勢.

一、基本公式

為了順利運用建立坐標系法解幾何壓軸題，需提前補充如下公式：

兩點間距離公式 若平面內兩個點A，B的坐標為A（x1，y1），B（x2，y2），則A，B兩點間的距離為|AE|=（x1-x2）2+（y1-y2）2.

點到直線距離 設直線l的方程為Ax+By+C=0，點P的坐標為（x0，y0），則點P到直線l的距離為|Ax0+By0+C|A2+B2.

兩直線垂直斜率關系 若兩直線都存在斜率y1=k1x+b1，y2=k2x+b，則k1·k2=-1.

中點公式 設A（x1，y1），B（x2，y2）是平面直角坐標系內任意兩點，則中點公式為x1+x22，y1+y22.

二、原題呈現及思路簡述

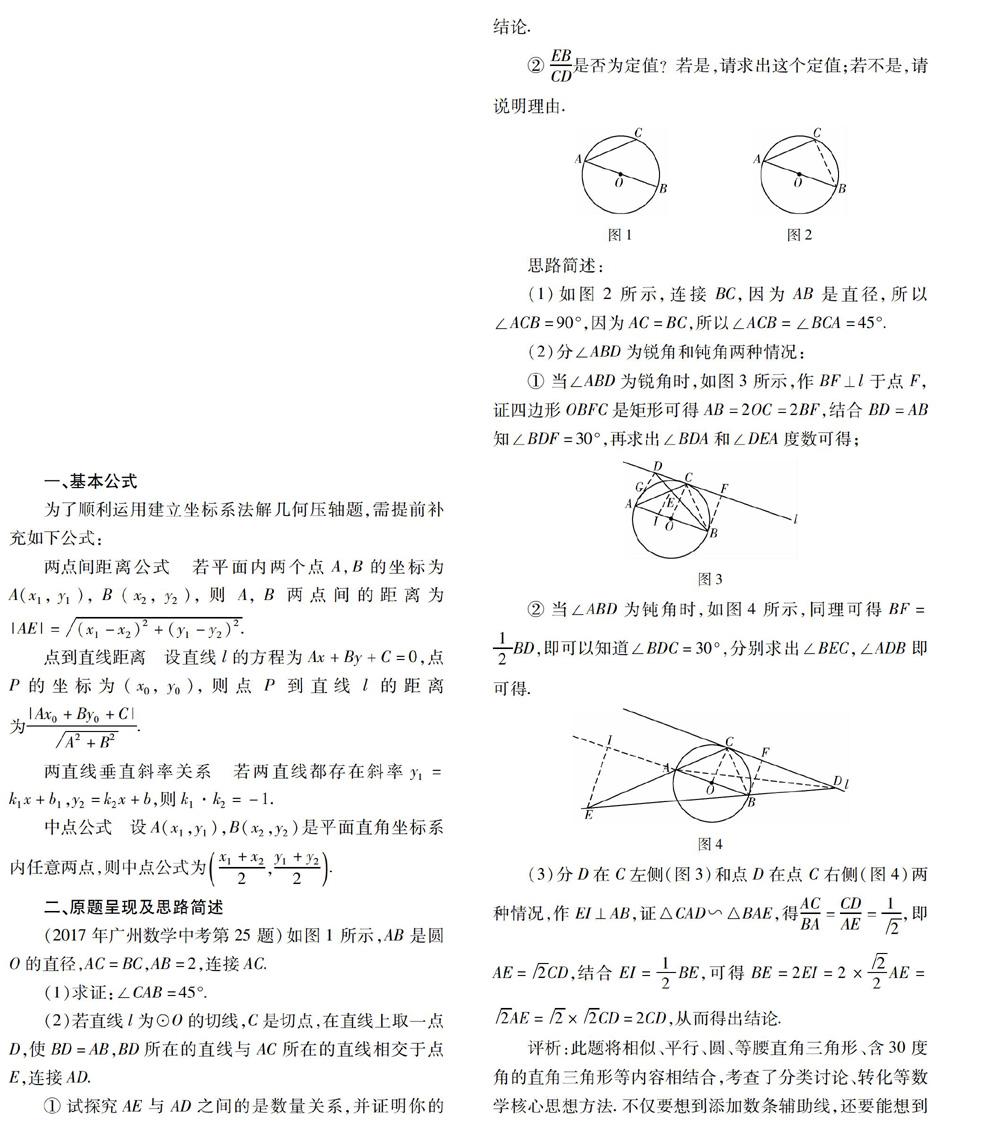
（2017年廣州數學中考第25題）如圖1所示，AB是圓O的直徑，AC=BC，AB=2，連接AC.

（1）求證：∠CAB=45°.

（2）若直線l為⊙O的切線，C是切點，在直線上取一點D，使BD=AB，BD所在的直線與AC所在的直線相交于點E，連接AD.

① 試探究AE與AD之間的是數量關系，并證明你的結論.

② EBCD是否為定值？若是，請求出這個定值;若不是，請說明理由.

思路簡述：

（1）如圖2所示，連接BC，因為AB是直徑，所以∠ACB=90°，因為AC=BC，所以∠ACB=∠BCA=45°.

（2）分∠ABD為銳角和鈍角兩種情況：

① 當∠ABD為銳角時，如圖3所示，作BF⊥l于點F，證四邊形OBFC是矩形可得AB=2OC=2BF，結合BD=AB知∠BDF=30°，再求出∠BDA和∠DEA度數可得;

② 當∠ABD為鈍角時，如圖4所示，同理可得BF=12BD，即可以知道∠BDC=30°，分別求出∠BEC，∠ADB即可得.

（3）分D在C左側（圖3）和點D在點C右側（圖4）兩種情況，作EI⊥AB，證△CAD∽△BAE，得ACBA=CDAE=12，即AE=2CD，結合EI=12BE，可得BE=2EI=2×22AE=2AE=2×2CD=2CD，從而得出結論.

評析：此題將相似、平行、圓、等腰直角三角形、含30度角的直角三角形等內容相結合，考查了分類討論、轉化等數學核心思想方法.不僅要想到添加數條輔助線，還要能想到∠DBF=30°這個關鍵點，但即使是學優生，要想在有限時間內找到這個關鍵點，也有很大困難.

三、建立坐標系法解題思路詳細分析

評析：這樣求解，我們發現問題的關鍵在于求出E點的坐標，則可求出AE，AD，EB，CD的長度，EBCD的值也易求出，而E點的坐標可看作是直線AC與直線BD的交點，只要建立方程組即可求出，這樣求解，思路清晰、簡潔.

四、教學思考

比較以上兩種解法，可以發現用建立坐標系法解此類幾何壓軸題避免了添加輔助線之苦，解題思路更簡捷、巧妙.當我們面對一道幾何壓軸題，感到“山重水復疑無路”時，可以嘗試用建立坐標系法去應對，興許你會感受到“柳暗花明又一村”之解題妙境.

“數缺形時少直覺、形少數時難入微”，著名數學家華羅庚的這句話深刻揭示了數形結合思想的重要性.溝通“數”與“形”的橋梁之一——平面直角坐標系，則是數形結合思想運用的典范.

如何巧妙建立坐標系，才能達到簡化運算的目的呢？筆者認為，可以考慮以下幾點：

第一，若圖形具有對稱性，可以利用其對稱性來建立平面直角坐標系，例如，可以選擇對稱中心為原點，對稱軸為坐標軸;第二，可以利用圖形中2條互相垂直的直線作為平面直角坐標系的對稱軸，此外，充分挖掘平面圖形的特征，結合平面幾何的性質或幾何意義來減少坐標參數，也能簡化解題過程.

無疑，用建立坐標系法解幾何壓軸題，思路清晰簡潔、易于上手.而幾何解法思考線路眾多，邏輯性強，需要較高的解題技巧.但任何事物都是一分為二的，一味運用建立坐標系法.有時會由于計算量大、數量關系復雜，使得思維受阻，有時還會將簡單問題復雜化，如上例第（1）小問，運用坐標系法反而顯煩瑣.因此，應注意將兩者有機結合、靈活選用，才能化繁為簡、大大提高學生解幾何壓軸題的能力.

【參考文獻】

[1]張傳法.建立空間直角坐標系，解立體幾何題[J].數學通訊，2004（6）：15-16.

[2]沈岳夫.巧用“坐標法”，妙解幾何綜合題[J].數理化學習，2015（7）：21-22.

[3]王震偉.巧建坐標系，妙解幾何題[J].中學數學教學參考，2015（26）：69-70.

[4]伍曉焰.2017年廣州市中考數學年報[R].廣州教育研究院，2017.