淺談泰勒公式在高考數學壓軸題中的應用

孫玉靜

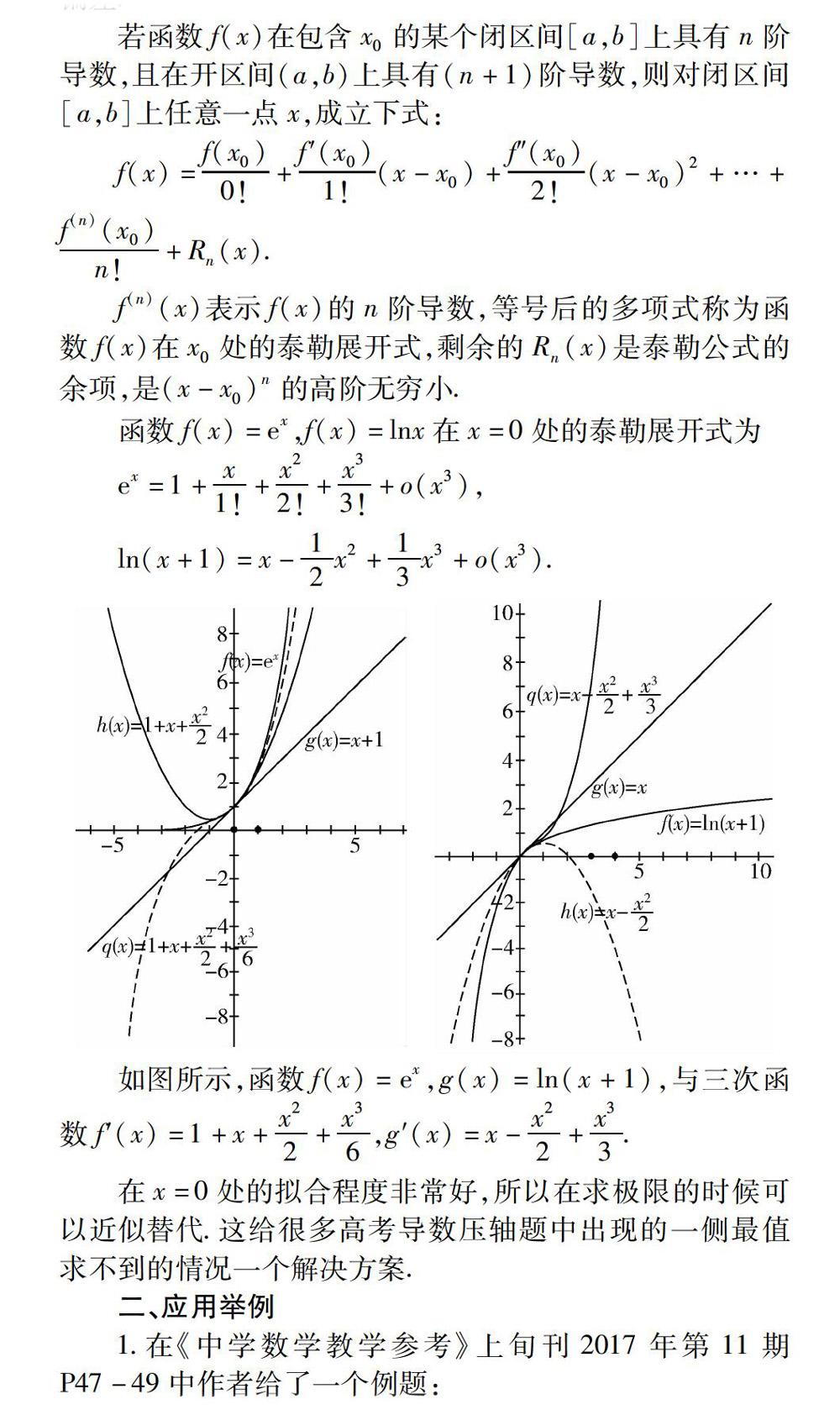
近年來，在各類測試和高考命題中，不等式ex≥x+1，lnx≤x-1都是出題者出題的一個很重要的出發點.上面的兩個不等式都是很容易證明的，追根溯源，這兩個不等式都來源于高等數學中的泰勒展開公式.本文在簡單介紹泰勒公式的基礎上，結合例題給大家呈現函數y=ex，y=lnx的泰勒公式在高考壓軸題中的應用.

一、背景介紹

數學中，泰勒公式是一個用函數在某點的信息描述其附近取值的公式.如果函數足夠平滑的話，在已知函數在某一點的各階導數值的情況下，泰勒公式可以用這些導數值做系數構建一個多項式來近似函數在這一點的鄰域中的值.泰勒公式還給出了這個多項式和實際的函數值之間的偏差.

三、備考啟示

1.隨著向量，算法，概率統計，導數等原來在大學才接觸的知識滲透到高中教材，高考作為選拔性的考試，試卷中也經常出現以高等數學為背景的試題.這類題目往往就是考查學生的知識遷移能力，綜合分析解決問題的能力，所以我們高中教師要更注意培養學生的數學思維能力及數學學科素養.

2.培養學生的認知能力.就是不光要教會學生如何應對考試中的各種題型，而且要培養學生站在出題者的高度去思考他們會從哪些角度出題.這就要求我們高中教師要用新課程標準審視常規教學，提高自己的教育科研能力，注重“高觀點”下的中學數學銜接問題.

3.從簡單到復雜，從直觀到抽象是學生學習的基本認知規律，所以有一些抽象的代數問題如果能以數形結合的方式幫助學生理解，學生的學習效果肯定會更好.這就要求我們教師要注意信息技術的應用.在教學中更多地運用數學學習心理學原理來更好的規劃課堂.

【參考文獻】

[1]范東暉.入乎其內，出乎其外——讓習題教學更有效[J].中學數學教學參考，2017（11）：47-49.

[2]曹世鵬.以高等數學為背景的高考數學試題的研究[J].中學數學研究，2016（6）：17-20.