基于LSTM網絡的短波天波信道分析及預測?

趙四方 馬啟原 李鐵楠

（1.中國人民解放軍92785部隊 綏中 125200）（2.中國人民解放軍91404部隊 秦皇島 066001）

1 引言

短波通信具有開通快，抗毀性強和維護費用低的特點，各國軍隊均進行了廣泛的研究。遠距離短波通信主要是依靠天波傳播的，其通信效果與電離層的變化特性有關，而電離層的反射特性是隨著時間、地點、頻率、季節、年份等不斷地變化的，屬于時變色散信道，一天之中的變化也是很大，它同時具有時間、頻率、空間三種選擇性衰落，且受太陽活動周期影響，這給短波通信資源的調度使用帶來了很大的不確定性。針對頻率的預測主要采用電離層預報模型。然而，傳統電離層的預報模型無法針對確定的天波電路模型進行分析。在具體短波天波通信時，迫切需要一種可以實現點對點的天波電路精準分析預測的模型［1～2］。

近幾年海軍的遠海活動次數不斷增加，積累了大量的遠海短波通信數據，反映了我海軍當前情況下真實的通信技術水平。在傳統理論計算方法與探測評估方法未能發揮需求作用的情況下，采用人工智能的方法，實現對歷史通信數據的有效利用，從歷史數據中總結出短波通信信道蘊藏的通信規律，探索基于人工智能技術輔助的通信組織方法，可為海軍短波通信資源調度使用提供輔助決策支撐。

2 相關概述

短波的天波通信是通過電離層的反射實現遠距離通信，電離層是影響短波天波通信質量的關鍵，其中包括電離層的晝夜特征、太陽黑子數目變化，工業電氣電磁噪聲等［3］。電離層參數預報方法很多，其中國際參考電離層模型IRI因其用途的廣泛性和在電離層研究領域的重要性，成為為電離層參數的國際技術標準。然而，傳統電離層的預報模型無法針對確定的天波電路模型進行分析［4］。在具體短波天波通信時，迫切需要一種可以實現點對點的天波電路精準分析預測的模型。為此文獻［5～7］均通過使用神經網絡方法實現短波天波信道的頻率預測。然而，以上文獻所使用的神經網絡算法均不具有記憶性，無法對隨時間序列變化的模型進行有效研究，因而無法得出天波電路的慢變化與快變化規律。

本文采用多層神經網絡算法，第一層長短期記憶網絡（Long Short-Team Memory，LSTM），是時間遞歸的神經網絡，屬于遞歸神經網絡中的一類，較BP神經網絡具有記憶性，更易處理與時間序列相關的問題。在LSTM網絡中存在三個邏輯門，分別為輸入門，輸出門與遺忘門。邏輯門通過固定的計算方法，分別實現LSTM網絡基本神經結構Cell對信息的接收，輸出與遺忘三個過程［8］。由于LSTM網絡具有遞歸性，選擇性輸入與輸出的特征，符合短波天波通信過程中分析信道變化性時的時間迭代性要求。

第二層深度神經網絡［9］（Deep Neural Network，DNN）是在感知機的基礎上組成，在網絡中加入了隱藏層，實現了神經網絡的多元輸入與多元輸出。深度神經網絡按照結構劃分為輸入層，隱藏層與輸出層。深度神經網絡中，每個感知機之間互相連接，故深度神經網絡又稱為全連接網絡［11］。本文中，DNN層作用是將LSTM層高維度堆疊序列轉化為與樣本相同的標準輸出序列，從而得到短波天波電路變化規律的預測結果。

在多層神經網絡訓練中，為避免梯度下降時達到局部極值點，使用小批量梯度下降法優化神經網絡訓練過程，利用Adam方法優化訓練器，并在該方法下測試平方和誤差函數與交叉熵誤差函數，以確定合適的損失函數。為避免模型出現過擬合現象，訓練過程中設置神經元以一定概率不參與神經網絡的訓練。

3 多層神經網絡的短波天波電路建模原理

神經網絡將短波天波電路的通信過程視作“黑箱”分析。由于發方固定站的通信設備參數資料不易獲取，故僅考慮接收方站相關參數變量。其中短波天波模型的無關變量為接收機地點、接收機型號以及接收天線型號；有關變量包括發射機位置，接收日期、接收時間、接收功率與接收信號強度。其中日期與接收時間兩個變量在模型建模中各自分開作為一個單獨變量，在變化規律分析過程中作為一個整體變量。本方案中，數據預處理，經過LSTM網絡與DNN網絡計算輸出結果。模型根據預測值與真實值的誤差結果確定神經網絡最優參數。最終與其他短波預測軟件進行比較，得出結論。流程如圖1所示。

圖1 方案流程圖

3.1 數據采集

方案通過查找國際短波頻率表，定位發信臺站的發信頻率及時間，通過接收設備接收模擬進行短波通信過程，并對接收信號進行記錄。其中記錄的主要內容包括：

1）信號的通信頻率，其頻率范圍為3MHz～30MHz。

2）信號的接收帶寬，按照國際標準，信號的接收帶寬設置為3.3kHz，頻率劃分成為8100個不同的信道。

3）信號的采集周期，信號的采集周期根據采集時間變化。

4）信號的采集時間段。

5）信號的接收功率，接收信號功率單位為dBm。

將采集到的信號按照時間序列排列，將樣本數據進行正則化處理。

3.2 神經網絡權值初始化方案

隱層神經元的權值初始值決定了神經網絡的初始結構和是否能達到梯度最小值的情況。

神經網絡隱層權重的迭代過程會因為激活函數不同而存在梯度消失（Vanishing Gradient Problem）和梯度爆炸（Exploding Gradient Problem）情況。由于logistic函數的均值總是大于0，導致隱層神經元趨于飽和，使用Xavier［12］方法，要求神經元的初始值應服從：

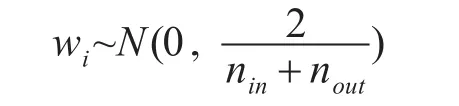
假設偏置為0，輸入為1，神經網絡學習速率為η，求得神經網絡迭代公式為

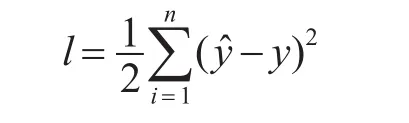
LSTM網絡使用logistic函數σ，神經網絡權值為W ，偏置為b，輸入為X，故公式為

其中nin與nout表示輸入層神經元個數與輸出層神經元個數。神經網絡偏置b的維度為（1，n），其中n代表下一神經層中神經元個數，偏置b的分布可以不做要求。

3.3 神經網絡損失函數

神經網絡的權值優化過程首先需要確定損失函數。損失函數包括平方和誤差函數（error sum of squares）與交叉熵損失函數（cross-entropy error）。

假設y?表示神經網絡輸出值，y表示真實值，平方和誤差函數l的公式為

3.4 神經網絡訓練器優化方案

優化器選擇Adam（Adaptive Moment Estimation，Adam）方法。其結合了Monentum和RMSProp的優化方法，保留了梯度下降時的動量保持情況，同時其利用梯度的一階矩陣估計與二階矩陣估計動態調整不同參數的學習速率［10～11］。假設其保持動量的能力為β1，一般情況下β1=0.9；梯度的二階估計為s，衰減速率為β2，一般情況下β2=0.999；?表示元素乘法，?表示元素除法，?為平滑變量，防止出現除以0的情況，一般情況下?=10-8。公式為

在訓練過程中采用小批量梯度下降算法（Mini-batch Gradaient Descent）。小批量梯度算法將數據劃分為多個不重合的數據子集，每一個子集作為一組訓練集進行訓練。相較于梯度下降算法，小批量梯度下降算法在訓練模型時具有更高的訓練效率與速度。

3.5 神經網絡結構設計

LSTM神經網絡結構包括時序（Sequence）與隱層神經網絡（Hidden Layer）結構。隱層神經網絡數目和神經元數目根據具體要求分為兩種情況。根據網絡的復雜度不同，神經網絡層數可以選擇平行關系的設計思路和遞進關系的設計思路。本文采用遞進關系設計的多層神經網絡，其中第一層LSTM層用于短波天波模型的時間變化規律分析；第二層采用深度神經網絡，用于對第一層輸出結果的抽取與標準化處理。其中LSTM神經網絡在多層神經網絡中發揮核心作用。

為了降低模型的過擬合風險，提高神經網絡的訓練速率，采用Dropout Regularization的方法有效提高神經網絡的準確率。Dropout Regularization實質是在每一次訓練中，除輸出層以外的神經元都以概率p不參與神經網絡的計算，鑒于每次有部分神經元不參與訓練，故使得每個參與訓練的神經元泛化性與神經元之間的合作更為緊密，對數據的細微變化不過于敏感。一般情況下p=0.5，實際工程中將根據模型反饋結構進行適當調整［13～14］。

4 短波天波電路的多層神經網絡模型

4.1 數據準備及預處理

樣本數據經正則化處理后，選擇每組樣本數據的序列長度，并將樣本數據劃分為訓練集

與測試集，滿足數據量比例為2：1。其中訓練集數據分為兩組，一組為X數據，另一組為Y數據，測試集數據劃分方法同訓練集數據。劃分算法如下。

輸入：樣本數據data

輸出：訓練集train_X，train_Y，測試集test_X，test_Y

步驟：（1）讀取樣本數據data；

（2）樣本數據正則化處理，得到數據normalized_data；

（3）計算訓練集數據長度 L1，測試集數據長度L2；

（4）for(索引=0，索引＜ L1-序列長度-1，索引=索引+1){

數組X=normalized_data[索引：索引+序列長度]；

數組Y=normalized_data[索引+1：索引+序列長度+1]；

添加一組X數據于train_X列表中；

添加一組Y數據于train_Y列表中；

}；

（5）for(索引=L1，索引＜ L1+L2-序列長度-1，索引=索引+1){

數組X=normalized_data[索引：索引+序列長度]；

數組Y=normalized_data[索引+1：索引+序列長度+1]；

添加X數據于test_X列表中；

添加Y數據于test_Y列表中；

}；

（6）更改train_X，test_X維度[-1，序列長度，輸入數據長度]；

更改train_Y，test_Y維度[-1，序列長度，輸出數據長度]；

4.2 LSTM神經網絡搭建及訓練

本方案采用四層神經網絡結構，按次序分別為輸入層（input_layer），隱層神經網絡1（hidden_layer1），隱層神經網絡2（hidden_layer2）與輸出層。其中輸入層輸入數據為train_X或test_X，通過神經網絡計算得到預測數據，通過損失函數與梯度下降算法實現神經網絡模型的優化。將準備的數據劃分為多個子數據集，使用Mini-batch算法進行網絡訓練。

輸入層神經網絡在訓練過程中使用Dropout方法，設置輸入神經元的損失概率為20%。在測試過程中輸入層神經元為全連接狀態。隱層神經網絡1結構為LSTM神經網絡層，通過循環方法設定不同Cell個數訓練神經網絡。設置Cell層使用Elu激活函數，隱層神經網絡2結構為深度神經網絡，使用Xavier方法，使初始化神經網絡權值符合截斷正態分布，并設定初始偏置為0.1，并將結果送入輸出層中。由輸出層輸出最終結構并送入損失函數中，通過Adam算法對梯度流進行反向計算并更新。神經網絡結構算法如下所示。

輸入：訓練集數據train_X,train_y，序列長度，學習速率，批量訓練組數

輸出：訓練模型

步驟：（1）for(訓練輪數=0，訓練輪數＜=20000，訓練輪數=訓練輪數+1){

for(迭代=0，迭代＜批量訓練組數，迭代=迭代+1){

2.1.2 準確度試驗 在未知土壤樣品中分別加入一定量的鋅、銅和鉻標準溶液，進行加標回收試驗來驗證方法的準確度。經測定，該方法鋅的回收率在98.0%～109.0%，銅的回收率在 92.0%～103.0%，鉻的回收率在95.0%～107.2%，準確度可以滿足試驗要求。

（2）#輸入層神經網絡

X_drop=Dropout(train_X)；

（3）#隱層神經網絡1

Cell=LSTMCell(神經元個數)；

Cell=Dropout(Cell)；

Output1=LSTM算法(Cell,X_drop,激活函數=ELU)

（4）#隱層神經網絡2

初始化權值W；

Output2=Output1×W+B；

（5）#輸出層

y_pred=更新Output2維度為[-1，序列長度，

輸出長度]

（6）損失值=損失函數(train_Y，y_pred)；

（7）Adam(學習速率)最小化損失值；

}；

}；

5 短波天波電路模型評估

5.1 模型評估方案

模型評估指標應具有代表性、客觀性與科學性。是對不同參數的神經網絡對短波天波電路的規律分析結果與預測結果進行分析判斷，最終得出最優模型的過程。應以短波天波電路的變化規律分析主要是根據計算不同模型相對最低點誤差之間的間隔進行分析，若為等比例間隔則表明短波天波電路時間變化規律與序列間隔時間成整數倍關系。在判斷短波天波電路規律后，針對功率預測的最優模型評估主要有以下三個標準：

1）模型的訓練集誤差與測試集誤差相對較低。

2）模型的預測結果可以大致反映未來一段時間內短波天波電路的變化趨勢。

3）不同模型在前兩條條件大致相同的情況下，將選擇訓練時間代價小的模型作為最優模型。

根據模型的評估方法將確定最優短波電路模型，并同短波預測軟件進行對比，得出多層神經網絡短波電路模型的優劣之處。

5.2 模型評估

5.2.1 9.75MHz電路評估

9750MHz為日本NHK廣播電臺信號，臺站位于日本東京市。數據收集了臺站5月21日至5月25日1900～2300接收機接收信號強度，接收規律為30s，接收數據2408條。對數據進行等間隔抽樣處理，間隔為180s，得到數據401條。數據預處理后如圖2所示。

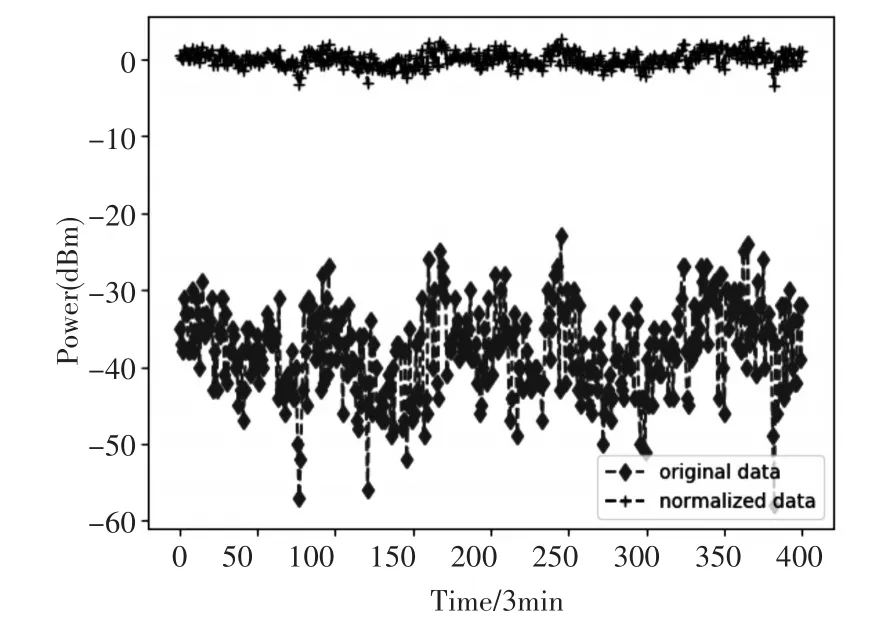
圖2 9.75MHz接收信號強度預處理

將數據劃分為訓練集和測試集后送入神經網絡中。設定信號的序列長度為5、10、15、20與25，則對應接收信號序列為 15min、30min、45min、60min與75min。設定LSTM Cell個數為2、5、10與20。為便于數據展示對不同模型進行編號。損失函數為平方和誤差函數則不同模型對應的測試集誤差，如表1～2所示。

表1 訓練集誤差

多次重復實驗結果表明，模型具有良好的收斂效果，且能反映出短波天波電路變化趨勢，圖2表示了5月23日1900～2300短波天波電路的實測值，短波預報軟件的預報值與神經網絡模型的預測值。其中橫坐標為數據采樣點，縱坐標為正則化處理后的功率值。經對比發現，神經網絡模型的預測結果相較于短波預測軟件結果更加貼近實測數據的變化情況，且相對誤差較小，預測精度高于短波預報軟件。

圖3 軟件預測，神經網絡預測與真實值比較

圖3 所反映的測試結果是訓練集數據為5月21日至5月22日的實測數據。若使用5月21日至5月23日實測數據預測5月24日，經過模型測試誤差有所上升，故得知9.75MHz短波天波電路的日變化規律大約為3天。

5.2.2 6.03MHz電路評估

6.03 MHz為中國國際廣播電視臺一臺，臺站位于北京。數據收集了臺站6月1日至6月3日0900-1000接收機接收信號強度，接收規律為3分鐘，接收數據119條。經數據預處理后如圖4所示。

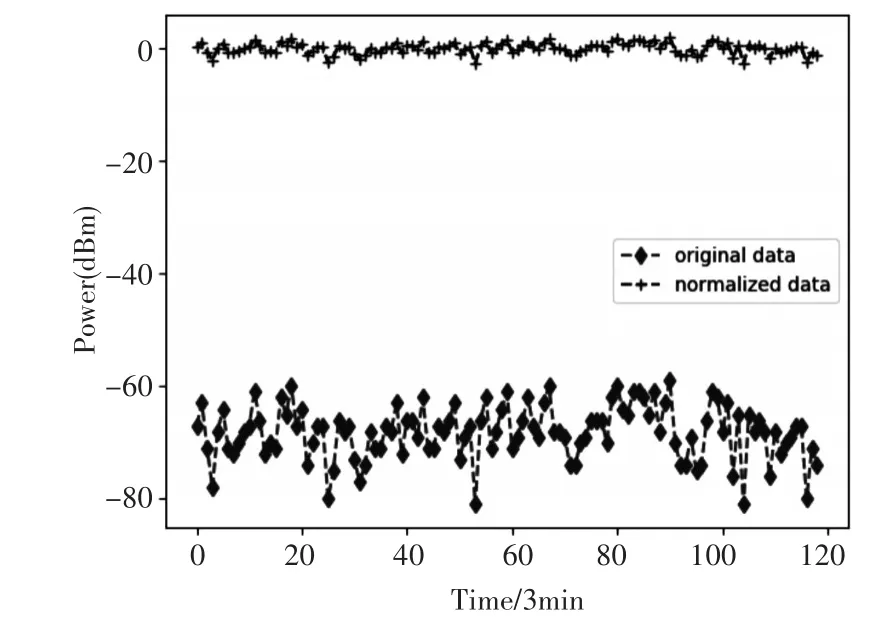
圖4 9.75MHz接收信號強度預處理

將數據劃分為訓練集和測試集后送入神經網絡中。設定信號的序列長度為5、10、15、20與25，則對應接收信號序列為 15min、30min、45min、60min與75min。設定LSTM Cell個數為2、5、10與20。為便于數據展示對不同模型進行編號。損失函數為平方和誤差函數則不同模型對應的測試集誤差，如表3所示。

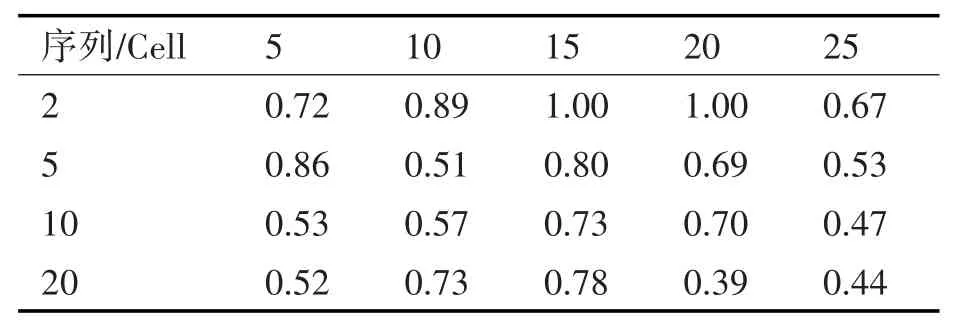
表3 訓練集誤差

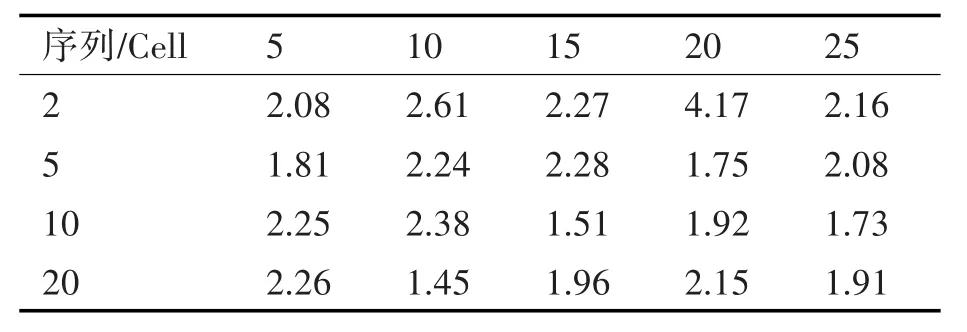
表4 測試集誤差

多次重復實驗結果表明，模型具有良好的收斂效果，且能反映出短波天波電路變化趨勢，適合6.03MHz電路模型。圖4表示了6月2日0900-1000短波天波電路的真實值，短波預報軟件的預報值與神經網絡模型的預測值。其中橫坐標為數據采樣點，縱坐標為正則化處理后的功率值。經對比發現，神經網絡模型的預測結果相較于短波預測軟件結果更加貼近實測數據的變化情況，且相對誤差較小，預測精度遠高于短波預報軟件。

圖5 軟件預測，神經網絡預測與真實值比較

圖5 所反映的測試結果是訓練集數據為6月1日實測數據。若使用6月1日至6月2日實測數據預測6月3日，經過模型測試誤差有所上升，故得知6.03MHz短波天波電路的日變化規律大約為2天。

6 結語

本文討論了時間因素對短波天波通信電路質量的影響，結合神經網絡原理與算法，構建了擬合短波天波電路通信的模型。采集了短波天波電路在不同距離、不同方向與不同距離的通信數據。將采集的數據送入優化后的多層神經網絡進行運算，調整神經網絡參數，最終擬合出適用于不同短波天波通信電路的模型，分析得到了電路時序的日變化與分鐘變化的規律性，并對其進行預測，并同實測值與現有短波預測軟件預測結果進行比較，證明模型在預測的精度上高于現有短波預測軟件，并驗證了多層神經網絡可用于短波天波電路建模中。

其中重點完成了使用該短波天波電路下的最優參數神經網絡模型，根據不同天數的采集數據重新劃分訓練集與測試集，調整訓練集與測試集比例，分析電路的天變化規律，并將預測結果同現有短波預測軟件與測試集數據相比較，分析電路模型的優劣。

在本文中也存在一些不足：1）實驗過程中模擬通信過程不能完全模擬正常通信，無法對通信的時間段，通信方式以及發方功率進行調整；2）通信數據數量不足；3）固定參數模型容易受到其他無關變量的影響。