連發(fā)射擊下某輕型高機(jī)動(dòng)平臺(tái)振動(dòng)特性研究

范天鋒，王在森，寧變芳，張?zhí)?/p>

(西北機(jī)電工程研究所，陜西 咸陽(yáng) 712099)

某高炮采用輕型高機(jī)動(dòng)底盤，該底盤采用一體式承載車身設(shè)計(jì)，具有車身輕、承載能力高的特點(diǎn)；采用的柔性車架，使車架壽命提高3倍以上；該底盤前后均采用了雙橫臂螺旋彈簧獨(dú)立懸架，可適應(yīng)較大的地面落差，而大尺寸胎面與起伏路面附著幾率的提高，提升了越野性能。在射擊載荷工況下，瞬時(shí)連發(fā)沖擊載荷的作用使平臺(tái)呈現(xiàn)出典型的動(dòng)態(tài)振動(dòng)特性。

陳欣等[1]對(duì)帶獨(dú)立懸架的8×8多軸輪式車輛通過(guò)連續(xù)障礙的性能進(jìn)行了建模仿真，在建模過(guò)程中對(duì)懸架變形、車輪懸空等問(wèn)題進(jìn)行了分析；左振玉等[2]對(duì)多軸雙橫臂獨(dú)立懸架輪式車輛靜態(tài)軸荷研究，提出了獲取軸荷的新方法；吳雪蛟等[3]運(yùn)用多剛體離散元法快速建立車架有限自由度柔體模型的方法，所建模型可方便用于后續(xù)結(jié)構(gòu)優(yōu)化；芮強(qiáng)等[4]建立了包含柔性車體結(jié)構(gòu)的多軸輪式車輛剛?cè)狁詈蟿?dòng)力學(xué)模型,對(duì)比分析了兩種典型道路上動(dòng)態(tài)載荷作用下車體結(jié)構(gòu)的應(yīng)力。以上文獻(xiàn)均未涉及雙橫臂螺旋彈簧獨(dú)立懸架建模及連發(fā)射擊載荷下輕型高機(jī)動(dòng)平臺(tái)的振動(dòng)特性研究。

為了掌握該平臺(tái)在靜止射擊時(shí)的振動(dòng)特性，基于多剛體動(dòng)力學(xué)，結(jié)合空間“RRSS”四連桿機(jī)構(gòu)硬點(diǎn)匹配，構(gòu)建了雙橫臂螺旋彈簧獨(dú)立懸架模型；為了考慮車架彈性對(duì)平臺(tái)振動(dòng)的影響，建立了基于歐拉多段梁?jiǎn)卧膹椥攒嚰苣Ｐ停煌ㄟ^(guò)懸架K&C試驗(yàn)驗(yàn)證了柯曼太半經(jīng)驗(yàn)輪胎剛度計(jì)算模型的準(zhǔn)確性，并計(jì)算了該底盤輪胎的垂直剛度；在連發(fā)射擊條件下，對(duì)高低0°射角、方位90°的平臺(tái)振動(dòng)特性進(jìn)行了仿真計(jì)算，經(jīng)與實(shí)彈射擊試驗(yàn)平臺(tái)振動(dòng)測(cè)試曲線對(duì)比，驗(yàn)證了仿真模型的精度，為該類底盤的建模與分析提供了有益的指導(dǎo)，同時(shí)為該武器系統(tǒng)總體參數(shù)匹配與優(yōu)化奠定基礎(chǔ)。

1 底盤模型的建立

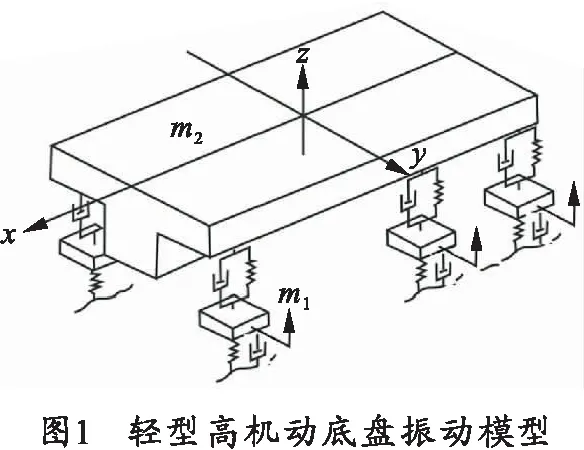
汽車底盤是一個(gè)復(fù)雜的振動(dòng)系統(tǒng)，應(yīng)根據(jù)所分析的問(wèn)題進(jìn)行簡(jiǎn)化。圖1為把汽車車身質(zhì)量看作為一個(gè)剛體的立體模型。汽車的懸掛(車身)質(zhì)量為m2(簧載質(zhì)量或簧上質(zhì)量)，它由車身、車架及其上的總成所構(gòu)成。懸掛質(zhì)量通過(guò)減振器和懸架與車軸、車輪相連接。車輪、車軸構(gòu)成的非懸掛(車輪)質(zhì)量為m1(非簧載質(zhì)量或簧下質(zhì)量)。車輪再經(jīng)過(guò)具有一定彈性和阻尼的輪胎支承在路面上。在分析車體振動(dòng)時(shí)，車身有3個(gè)平動(dòng)自由度和3個(gè)旋轉(zhuǎn)自由度，主要考慮航向、俯仰(縱搖)、側(cè)傾(橫滾)，共6個(gè)自由度，6個(gè)車輪有6個(gè)垂直自由度和6個(gè)繞垂直方向旋轉(zhuǎn)自由度共12個(gè)自由度。整個(gè)輕型高機(jī)動(dòng)底盤具有18個(gè)自由度。

1.1 輪胎剛度獲取

輪胎剛度是進(jìn)行整車建模與仿真研究的必要條件，輪胎剛度的確定一般通過(guò)懸架K&C試驗(yàn)獲取或半經(jīng)驗(yàn)公式估計(jì)。輪胎徑向剛度計(jì)算示意如圖2所示。

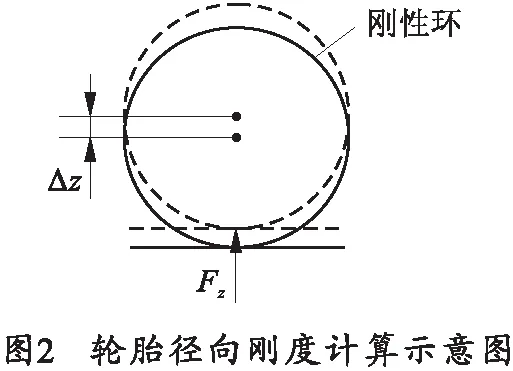
輪胎的徑向彈性除了受到輪胎外形尺寸的影響,輪胎的內(nèi)壓也是影響輪胎徑向彈性的主要因素,匈牙利柯曼太以各種輪胎尺寸與胎壓在混凝土路面上進(jìn)行了大量實(shí)驗(yàn),提出了輪胎壓縮量的經(jīng)驗(yàn)公式為

(1)

輪胎徑向剛度經(jīng)驗(yàn)公式為

(2)

式中：Δz為輪胎壓縮量，mm；Kz為輪胎徑向剛度，N/mm；C1為與輪胎結(jié)構(gòu)有關(guān)的參數(shù)；Fz為輪胎徑向載荷,N；p為輪胎壓力，kPa；D為輪胎自由直徑，cm；B為輪胎寬度，cm；K為與輪胎扁平比相關(guān)常數(shù)。

為了提高高機(jī)動(dòng)平臺(tái)建模精確性，對(duì)建模過(guò)程的關(guān)鍵環(huán)節(jié)進(jìn)行模型驗(yàn)證。根據(jù)吉林大學(xué)汽車仿真與控制國(guó)家重點(diǎn)實(shí)驗(yàn)室K&C懸架試驗(yàn)[5]，對(duì)輪胎型號(hào)為195/60 R15，胎壓210 kPa進(jìn)行了試驗(yàn)測(cè)試，實(shí)測(cè)該輪胎胎體徑向剛度為212.5 N/mm，如圖3所示。

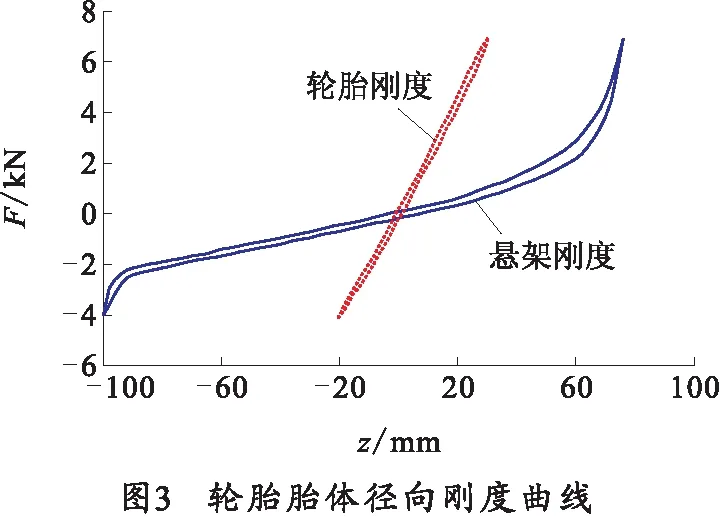
應(yīng)用式(2)計(jì)算出該輪胎195/60 R15在試驗(yàn)條件下的徑向剛度為224.2 N/mm，經(jīng)驗(yàn)公式與試驗(yàn)測(cè)試胎體徑向剛度相對(duì)誤差在6%以內(nèi)，驗(yàn)證了該經(jīng)驗(yàn)公式的準(zhǔn)確性，進(jìn)一步說(shuō)明柯太曼輪胎剛度計(jì)算公式可以滿足工程計(jì)算需求。

該高機(jī)動(dòng)平臺(tái)底盤輪胎采用大直徑、寬斷面、無(wú)內(nèi)胎子午線輪胎，中央充放氣系統(tǒng)，輪胎氣壓連續(xù)可調(diào)。輪胎規(guī)格：37×12.5 R16.5LT，利用柯曼太公式，計(jì)算出該輕型高機(jī)動(dòng)平臺(tái)的輪胎垂直剛度為433 N/mm.

1.2 雙橫臂螺旋彈簧獨(dú)立懸架模型

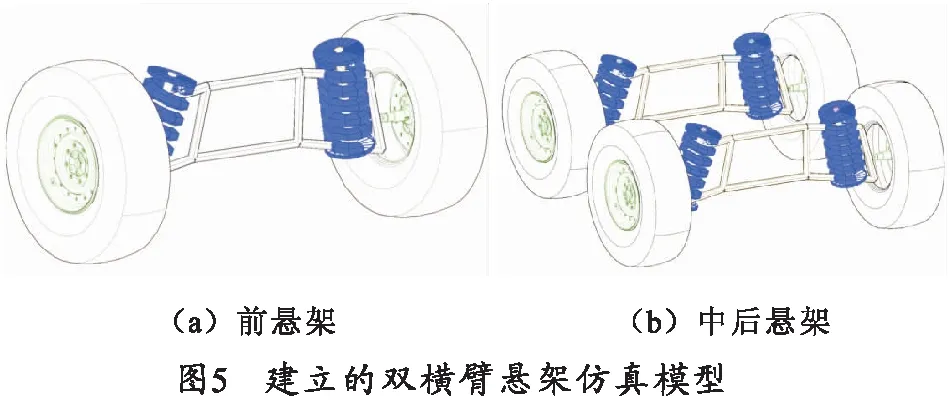
該輕型高機(jī)動(dòng)平臺(tái)底盤前后均為雙橫臂螺旋彈簧獨(dú)立懸架，雙橫臂獨(dú)立懸架導(dǎo)向機(jī)構(gòu)是一個(gè)空間“RRSS”四連桿機(jī)構(gòu)。

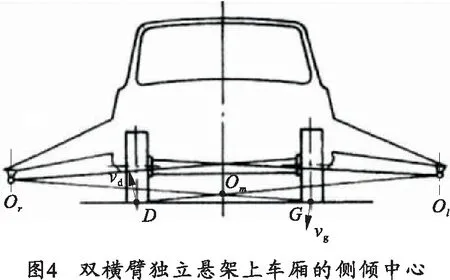
要確定雙橫臂獨(dú)立懸架輪胎與地面接觸點(diǎn)的速度矢量，需要應(yīng)用到“三心定理”。即四連桿機(jī)構(gòu)中，三根桿件的三個(gè)相對(duì)運(yùn)動(dòng)瞬時(shí)中心位于同一直線上。雙橫臂獨(dú)立懸架左右兩側(cè)的導(dǎo)向桿系與車廂各為一個(gè)四連桿機(jī)構(gòu)，如圖4所示，故車輪組件對(duì)車廂運(yùn)動(dòng)的瞬時(shí)中心為Ol及Or.因此，地面上D、G兩點(diǎn)相對(duì)車廂的速度vd、vg，地面相對(duì)車廂的瞬時(shí)轉(zhuǎn)動(dòng)中心，即為vd、vg兩矢量垂線的交點(diǎn)Om，即車的側(cè)傾中心[6]。

該底盤的雙橫臂獨(dú)立懸架的彈性元件采用大行程螺旋彈簧，剛度計(jì)算公式為

(3)

式中：d為簧絲直徑，mm；D為彈簧中徑，mm；n為彈簧的有效圈數(shù)；G為切變模量，MPa；α為彈簧與垂直線的夾角。計(jì)算前、中、后懸架的垂直剛度分別為187、253、253 N/mm.

根據(jù)雙橫臂懸架空間運(yùn)動(dòng)關(guān)系，應(yīng)用多體動(dòng)力學(xué)理論建立了雙橫臂懸架運(yùn)動(dòng)數(shù)學(xué)模型如圖5所示。

1.3 基于歐拉梁的彈性車架建模

考慮到車架彈性變形對(duì)平臺(tái)振動(dòng)特性的影響，基于歐拉梁?jiǎn)卧⒘硕喽瘟簭椥攒嚰苣Ｐ汀榱蓑?yàn)證該彈性車架模型的精度，同時(shí)建立了實(shí)際車架梁的有限元模型，分別對(duì)兩個(gè)模型進(jìn)行了固有特性分析與計(jì)算，計(jì)算模型如圖6、7所示，固有特性計(jì)算結(jié)果如表1所示。從對(duì)比計(jì)算結(jié)果可以看出，將車大梁簡(jiǎn)化為歐拉梁?jiǎn)卧邢薅尉哂休^好的計(jì)算精度，由于其單元數(shù)量較少，其計(jì)算效率可以大幅度提高。

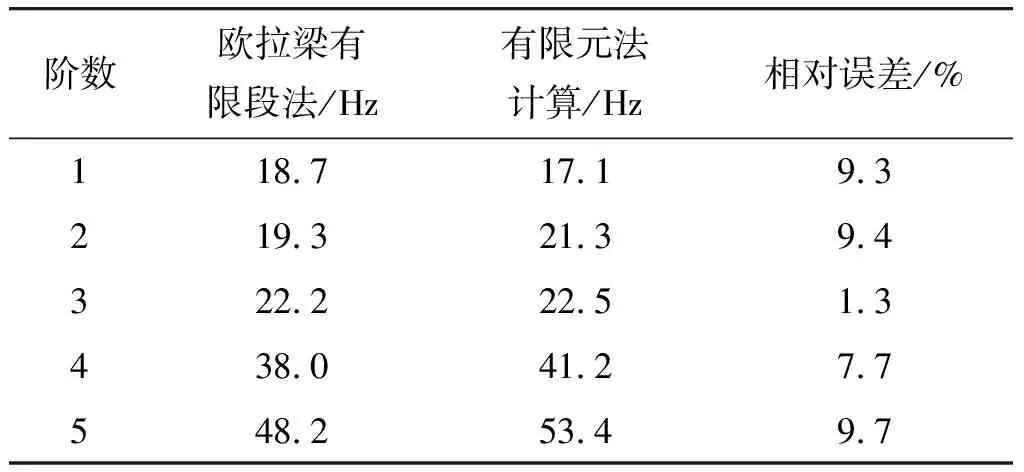
表1 歐拉梁有限段法與有限元法計(jì)算模態(tài)對(duì)比

應(yīng)用多體動(dòng)力學(xué)仿真軟件建立包含輕型高機(jī)動(dòng)平臺(tái)底盤系統(tǒng)的輪胎、雙橫臂懸掛，彈性車架及其車身結(jié)構(gòu)剛?cè)狁詈蟿?dòng)力學(xué)模型，整個(gè)輕型高機(jī)動(dòng)平臺(tái)底盤具有18個(gè)自由度，簡(jiǎn)化模型如圖8所示。

2 連發(fā)射擊載荷

射擊載荷根據(jù)轉(zhuǎn)膛自動(dòng)機(jī)彈簧液壓浮動(dòng)機(jī)原理計(jì)算得到，在炮膛合力作用下，經(jīng)彈簧液壓式浮動(dòng)機(jī)緩沖后將載荷傳遞給炮塔繼而傳遞給高機(jī)動(dòng)平臺(tái)。

浮動(dòng)機(jī)、炮塔以及高機(jī)動(dòng)平臺(tái)結(jié)構(gòu)布局參數(shù)如圖9所示。B為回轉(zhuǎn)中心到前輪中心的距離；L1為前輪中心到中輪中心的距離；L2為中輪中心到后輪中心的距離；H為火線高，布局參數(shù)如表2所示。根據(jù)火力炮塔的火線高及浮動(dòng)機(jī)后坐阻力作用位置，即可確定高機(jī)動(dòng)平臺(tái)射擊載荷激勵(lì)。

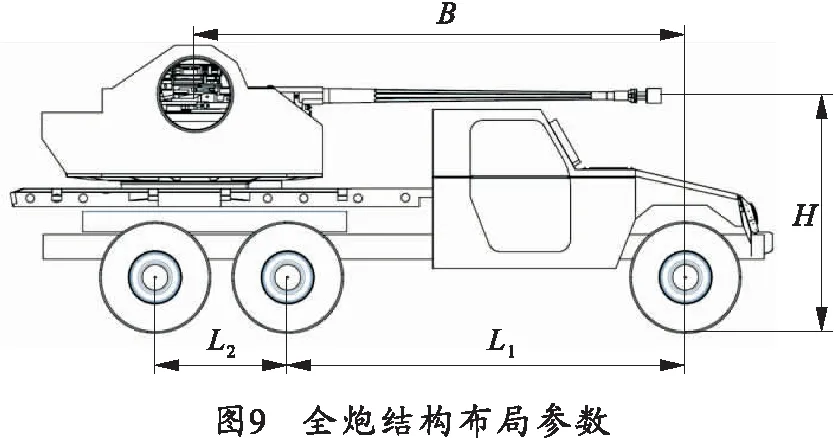
表2 系統(tǒng)布局參數(shù)表

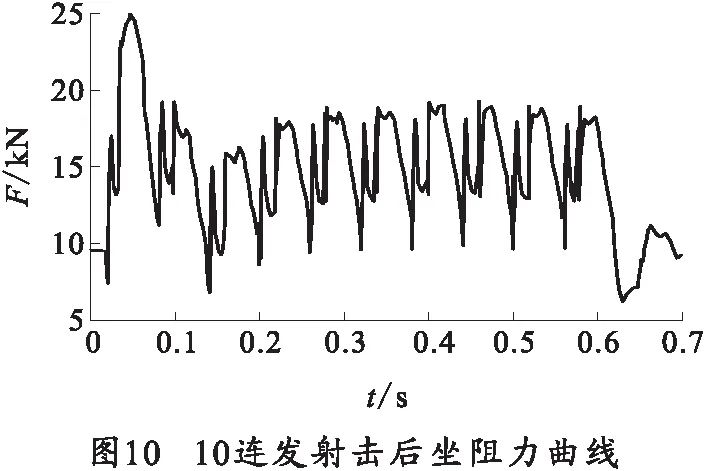
根據(jù)轉(zhuǎn)膛自動(dòng)機(jī)射速及點(diǎn)射長(zhǎng)度，計(jì)算時(shí)取射速1 000 發(fā)/min，點(diǎn)射長(zhǎng)度10連發(fā)，高機(jī)動(dòng)平臺(tái)所受的射擊載荷激勵(lì)如圖10所示。

3 與試驗(yàn)測(cè)試結(jié)果的對(duì)比

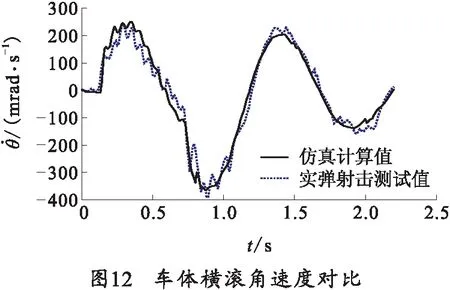
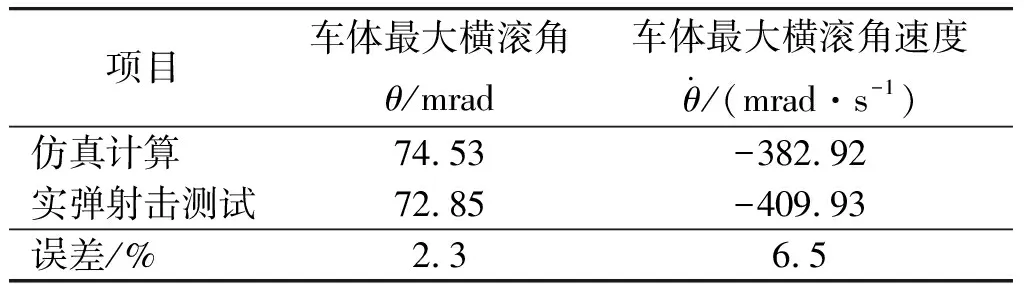
表3 仿真計(jì)算結(jié)果與測(cè)試結(jié)果對(duì)比表

從計(jì)算結(jié)果可以看出，該輕型高機(jī)動(dòng)平臺(tái)橫滾振動(dòng)頻率約0.97 Hz；在連發(fā)射擊條件下，當(dāng)射擊時(shí)間達(dá)到約570 ms時(shí)，射彈數(shù)第8發(fā)時(shí)，計(jì)算平臺(tái)橫滾角位移達(dá)到最大值74.53 mrad，高精度姿態(tài)陀螺測(cè)試平臺(tái)最大橫滾角位移為72.85 mrad，最大橫滾角計(jì)算誤差2.3%；仿真計(jì)算車體最大橫滾角速度382.92 mrad/s，實(shí)彈射擊實(shí)測(cè)車體最大橫滾角速度409.93 mrad/s，計(jì)算誤差6.5%.說(shuō)明高機(jī)動(dòng)平臺(tái)動(dòng)力學(xué)模型能夠較好地反映平臺(tái)的基本特性，可用于指導(dǎo)后續(xù)改進(jìn)及設(shè)計(jì)。

4 結(jié)束語(yǔ)

以某輕型高機(jī)動(dòng)武器平臺(tái)為研究對(duì)象，構(gòu)建了雙橫臂螺旋彈簧獨(dú)立懸架模型及基于歐拉梁的彈性車架模型，利用輪胎壓縮量的經(jīng)驗(yàn)公式獲取輪胎垂直剛度，對(duì)連發(fā)射擊條件下的平臺(tái)振動(dòng)特性進(jìn)行了分析計(jì)算，經(jīng)測(cè)試數(shù)據(jù)對(duì)比，驗(yàn)證了仿真模型的精度。

計(jì)算出的平臺(tái)振動(dòng)特性規(guī)律可為瞄準(zhǔn)線穩(wěn)定技術(shù)方案的確定提供理論依據(jù)，同時(shí)為開(kāi)展系統(tǒng)總體參數(shù)匹配與優(yōu)化奠定技術(shù)基礎(chǔ)。