一級氣體炮內彈道方程修正及仿真驗證

熊 鎬，王惠源，王玲儒

(1.中北大學 機電工程學院，山西 太原 030051；2.石家莊經濟學校，河北 石家莊 050000)

氣體炮是一種利用壓縮氣體作為動力源驅動彈丸運動的發射裝置。氣體炮相比于傳統火炮，在獲得較高初速時，彈丸需要承受的加速度和應力較小；發射過程中不存在高溫特性，使用壽命長；發射穩定性高，安全可靠。1946年，美國研究成功第一門利用輕質氣體作為動力源的一級氣體炮[1]。此后，氣體炮的研究引起了世界各國的廣泛興趣。

研究人員對氣體炮內彈道進行了多方面的研究，趙俊利等[2]分析了影響氣體炮內彈道的因素，推導出實用的氣體炮內彈道方程，在具體數值計算上進行了簡化，該方程在本文中稱之為經典方程；趙希欣等[3]應用氣體動力學理論及配合間隙的影響建立考慮氣體泄漏的內彈道模型；胡靜等[4]分析了氣體炮不同氣體工質的做功能力，并推導了不同工質在真空中自由膨脹獲得極限速度的關系式。一級氣體炮內彈道計算大多是采用文獻[2]中的內彈道方程，通過引入虛擬質量系數的方式計算內彈道過程中的次要功，經火炮內彈道計算的反復驗證，內彈道計算中引入虛擬質量系數具有極高的可靠性；Mark Denny在文獻[5]中使用一種指數式的氣體炮內彈道方程，文獻[6]對比了文獻[2]與文獻[5]的內彈道方程，但并未引入次要功系數，而是直接加上阻力項，并通過實驗驗證，認為文獻[2]中的氣體炮內彈道方程具有更高的可靠性；李鋒等[1]在文獻[2]的內彈道方程的基礎上提出一種基于密度的修正方式，對一級氣體炮內彈道方程進行修正，并通過仿真驗證。

一級氣體炮內彈道計算經典方程是在火炮內彈道理論基礎上，通過理論分析和推導，獲得炮口初速與內彈道過程的解析表達。與火炮不同，氣體炮大多有較大的氣室容積，經典方程在氣室容積較大時出現極大的誤差，在實際應用中存在一定的局限性。文獻[1]中對炮管內氣體密度表達式進行修正，推導了新的氣體炮內彈道方程，并進行了仿真驗證，該方程在本文中稱之為修正方程1。但在實際使用中，修正方程1仍然存在一定的誤差。筆者在分析了經典方程和修正方程1的問題及原因的基礎上，對虛擬質量系數中的氣體動能修正項計算方法進行了修正，并推導了新的氣體炮內彈道方程，稱之為修正方程2，將之與經典方程、修正方程1以及數值仿真結果對比，完成了對氣體炮內彈道方程的修正及驗證，證明了修正方程2在氣體炮內彈道計算中具有更高的可靠性。

1 氣體炮內彈道方程

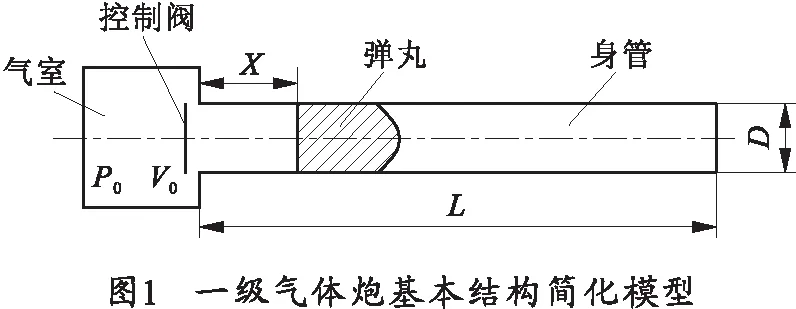
根據一般的一級氣體炮結構，建立一級氣體炮基本結構簡化模型，如圖1所示，P0為初始膛壓，V0為初始容積，L為身管長度，X為彈丸行程，D為氣體炮口徑。并有如下基本假設[2-4]：

1)氣室氣體視為理想氣體，整個內彈道過程認為是等熵絕熱膨脹過程，溫度始終為300 K，即氣體絕熱指數為常數。

2)不考慮彈前空氣阻力的影響，不考慮控制閥對氣流的影響。

3)各類能量損失在虛擬質量系數φ中考慮，不存在漏氣情況。

4)不考慮后效期氣體對彈丸的作用。

1.1 內彈道經典方程分析

基于上述假設，在理想狀態內彈道方程的基礎上，引入虛擬質量系數φ來計算各類能量損失，通過氣體動力學氣體絕熱方程計算膛內平均壓力，積分后得到氣體炮經典內彈道方程[2]：

(1)

式中：vm為彈丸初速；k為氣體絕熱指數；A為身管截面積；m為彈丸質量。

虛擬質量系數φ關系式為

(2)

式中：K為與摩擦力、彈丸旋轉等能量損耗有關的次要功系數，由實驗測得，此處取1.1；mg為氣體質量，式(2)等號右邊第2項為氣體運動功修正項。

根據理想氣體狀態方程，氣體質量mg為

(3)

式中：μmol為氣體摩爾質量；R為氣體常數；T為絕對溫度。

根據式(1)一級氣體炮內彈道經典方程，炮口初速隨氣室容積變化規律如圖2所示。可以看出，氣室容積較小時，計算結果與仿真結果基本相符，隨著氣室容積增大，仿真結果與計算結果的誤差逐漸增大；當氣室容積增大到一定程度，式(1)計算結果中，炮口初速呈下降趨勢，仿真結果炮口初速則隨著氣室容積增大而增大。對比圖2中的彈丸初速，發現初始壓力較大時，經典方程的計算結果與數值仿真結果偏差更大，可以認為，經典方程僅適用于氣室容積與初始壓力較小的一級氣體炮的內彈道計算。

1.2 內彈道修正方程1分析

氣體炮內彈道修正方程1認為，經典方程中密度ρ定義為氣體質量與炮管容積之比,沒有考慮氣室容積的大小，當氣室容積相對于炮管容積較大時，就會導致密度顯著增大，導致氣體附加質量人為變大，從而出現氣室容積越大炮口初速越小的情況[1]。

文獻[1]中將氣體密度表達式修正為

(4)

則虛擬質量系數φ表達式變為

(5)

氣體炮內彈道修正方程1：

(6)

根據式(6)一級氣體炮內彈道修正方程1，初始壓力P0=20 MPa，初始容積V0=50 L時，彈丸速度隨彈丸行程變化規律如圖3所示。可以看出，彈丸行程較小時，計算結果與仿真結果基本相符，隨著彈丸行程增大，仿真結果與計算結果的誤差逐漸增大。

1.3 內彈道修正方程2推導

通過對一級氣體炮內彈道經典方程推導過程分析，與數值仿真對比，認為內彈道經典方程忽略了氣室容積對膛內氣體的影響；內彈道修正方程1雖然考慮了氣室容積的影響，但是忽略了氣室形狀對氣體的影響，由氣體動力學理論可知，氣室直徑與身管口徑的差異會造成管內氣流狀況與假設情況有差別。

通過對火炮內彈道分析，氣體運動功E表達式為

(7)

式中，vX為該時刻的流速。

根據氣體質量均勻分布假設：

(8)

假設氣體速度按線性分布：

(9)

將式(8)、(9)帶入到式(7)中并積分，得：

(10)

式中,K0即為虛擬質量系數中的氣體運動功修正項。在K0的推導中，并未考慮氣室截面積和身管截面積的差異，事實上，氣體炮往往有較大的氣室容積，考慮到氣室到身管的縮徑情況，K0必須修正。修正方程1針對氣體密度的修正方式，考慮到了氣室容積的影響，但未考慮氣室到身管的縮徑情況，所以造成了隨著彈丸行程增大，彈丸速度誤差越來越大的情況。定義氣室擴大系數為χ，彈丸相對行程長為Λ，模型如圖4所示[7]。

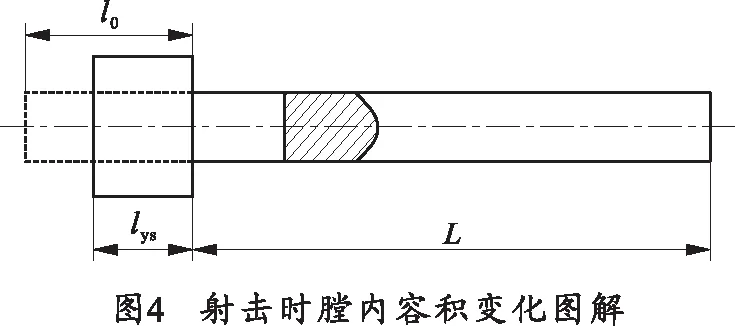
則：

(11)

(12)

式中：l0為氣室縮徑長；lys為氣室長。則：

(13)

那么，虛擬質量系數φ1的關系式變為

(14)

由式(14)可以看出，新的虛擬質量系數φ1比修正方程1的虛擬質量系數φ增加了有關氣室結構的修正項。

根據彈丸運動方程，彈丸的速度為

(15)

式中，P為平均膛壓，根據熱力學基本方程，平均膛壓為

(16)

將式(14)、(16)代入式(15)并積分，則：

(17)

式(17)即為一級氣體炮內彈道修正方程2.

2 氣體炮內彈道方程對比驗證

為了驗證修正方程2的可靠性，利用流體仿真軟件FLUENT對一級氣體炮內彈道過程進行數值仿真，在與理論計算相同假設條件下對不同氣體工質(氫氣、氦氣、空氣)在不同氣室容積下的彈丸膛內運動過程仿真。仿真過程相關設置如下：

1)仿真采用壓力基瞬態求解器，由于氣體炮內彈道過程中，氣室壓力在極短的時間內有極大的變化，縮短時間步長有利于提高彈丸速度計算精度，時間步長設為1 μs，計算總時間為0.01 s，每一步循環次數為30.

2)利用FLUENT動網格技術，采用二維結構化網格，發射過程中膛內流場區域內的網格會隨著彈丸運動不斷變化，數值仿真過程中應用彈性光順法和動態分層法相結合的網格更新技術，保證膛內流場的網格質量與計算精度。

3)采用SST 湍流模型，求解控制選用couple算法一階迎風格式對內彈道過程中膛內流場情況進行計算。

4)編寫用戶自定義函數(UDF)嵌入到FLUE-NT中，實現讀取彈底壓力變化情況，并定義阻力項，根據彈底壓力變化情況，計算膛內任意時刻彈丸運動情況。

主要仿真參數:彈丸質量m=1 kg；身管截面積A=0.785 dm2；身管長L=5 m.

氣室容積V0=50 L，初始壓力P0=20 MPa，氣體工質為氦氣時，彈丸出膛口瞬間膛內壓力分布與速度分布如圖5～8所示。可以看出，氣流從氣室到身管，縮徑造成氣流速度快速增加和壓力的快速降低，可見氣室形狀對膛內流場的影響不容忽視。

在不同氣室容積和不同氣體工質情況下，3種修正方程以及數值仿真結果對彈丸初速的對比如表1所示。其中容積比r為

(18)

表1、圖9、10為經典方程、修正方程1、修正方程2與數值仿真結果在不同氣室容積下的計算結果對比。

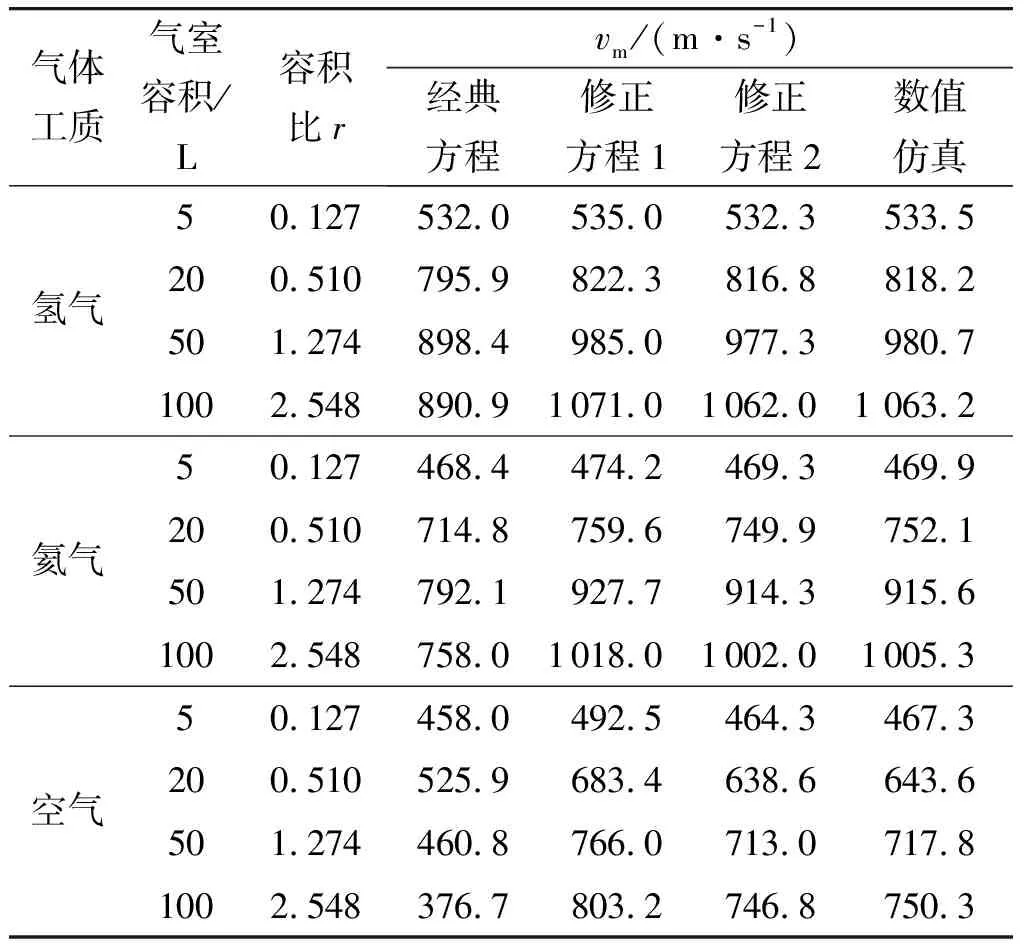
表1 計算結果對比(L=5 m，P0=20 MPa)

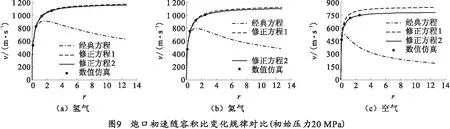
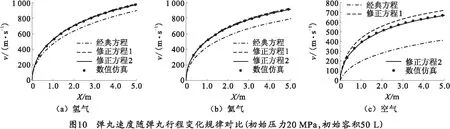
結合圖9、10和表1可以看出：

1)當容積比較小時，3種一級氣體炮內彈道方程計算出的彈丸初速曲線基本重合，且與數值仿真結果一致；但隨著容積比的增大，經典方程出現容積比增大彈丸初速減小的情況，修正方程1與數值仿真結果基本一致，但依舊存在一定的誤差，修正方程2則與數值仿真結果始終保持較高的一致性。

2)對比3種不同氣體的計算結果，當氣體工質為氫氣時，修正方程1、修正方程2和數值仿真三者所得結果偏差很小，當氣體工質為氦氣時，三者所得結果出現了一定的偏差，當氣體工質為空氣時，三者計算結果出現了極大的偏差。但不論哪一種氣體工質，修正方程2所得結果都更接近數值仿真結果。

3)3種內彈道方程計算所得彈丸膛內速度變化規律基本相同，但修正方程2的計算結果與數值仿真的結果更接近。

3 結論

一級氣體炮內彈道方程是從火炮內彈道理論中演化而來，火炮的彈膛容積比往往較小，且膛壓較大，忽略氣室結構尺寸來簡化計算不會造成太大誤差，因此氣體炮內彈道經典方程在容積比較小時，計算結果與實測結果偏差較小，基本可以滿足工程設計要求。

與火炮不同，氣體炮往往有較大的氣室容積，修正方程1和修正方程2都考慮了氣室結構對一級氣體炮內彈道的影響，進而對內彈道方程進行修正。修正方程1通過對密度表達式進行修正推導出新的氣體炮內彈道方程，相比于經典方程，修正方程1考慮了氣室容積對氣體炮內彈道的影響，具有更廣的使用范圍和更高的可靠性，但是未考慮從氣室到身管的縮徑對氣流的影響。由于修正項最終作用到虛擬質量系數中的氣體運動功修正項上，由氣體動力學可知，縮徑對氣流有加速作用，忽略縮徑就造成了氣體運動功計算結果小于實際的氣體運動功，因此彈丸運動功相應地增加，計算出的彈丸速度也高于實際的彈丸速度，這也就造成了修正方程1在計算分子質量較大的氣體工質內彈道時誤差較大。修正方程2考慮了氣室容積和氣室結構對膛內流場的影響，對虛擬質量系數中的氣體運動功項進行修正。

修正方程2與經典方程、修正方程1以及數值仿真結果對比表明：在容積比較小時，3種內彈道方程計算結果基本一致；但是在容積比較大時，經典方程計算結果與數值仿真結果出現較大偏差；與數值仿真結果對比，修正方程1相比于修正方程2存在較大誤差，且當氣體工質分子質量較大時，誤差也隨之增大，而修正方程2計算結果與數值仿真結果始終表現出較高的一致性，證明了修正方程2的正確性與適用性。