基于磁流變阻尼器的火炮懸架振動控制研究

王 明，童仲志，侯遠龍，胡 達，項 軍

(南京理工大學 機械工程學院，江蘇 南京 210094)

為進一步提高自行火炮的機動性能，不僅僅是增加發動機的功率，一個重要的制約因素就是地面激勵所引起的振動問題沒有得到很好的解決[1]。針對輪式自行火炮，良好的懸架系統不僅有助于改善車輛行駛的平順性和操縱穩定性，同時也能一定程度上提高自行火炮行進間的射擊精度。懸架系統振動控制分為被動、主動和半主動3種，其中以磁流變阻尼器(magnetorheological damper,MR阻尼器)構成的半主動懸架由于其優良的性能已被廣泛的應用于車輛懸架系統中[2]。

目前，應用于車輛半主動懸架的控制策略主要有天棚控制[3]、地棚控制[4]、最優控制[5]、模糊控制[6]和神經網絡控制[7]等。其中天棚、地棚控制相較于其他控制方法具有成本低廉、實現方法簡單，所需狀態量少等優點，因此成為一些學者研究的重點。文獻[8]比較了天棚、地棚控制的優點，提出了一種混合控制策略并將其應用于高速列車的振動控制中，結果表明混合控制相較于純天棚、地棚控制對車輛振動的抑制效果較好，可以使車輛具有較高地綜合性能。文獻[9]以混合控制為基礎，研究了控制器中各參數的改變對車輛性能的影響，仿真結果表明，當各參數達到最優匹配時可以進一步地提高車輛的減振效果。文獻[10]采用了免疫算法對混合控制器的參數進行優化，仿真結果表明經優化后的混合控制可以同時兼顧車輛的平順性和操縱穩定性，提高了懸架的整體性能。

綜上可知，在混合控制的前提下，通過引入適當的算法對控制器的參數進行優化可以進一步提高系統的減振效果。因此，筆者以自行火炮懸架作為研究對象，建立了天棚、地棚混合控制器，鑒于粒子群算法具有搜索速度快，效率高等優點，采用粒子群算法對控制器的參數進行優化。選擇刻畫精度較高的變換現象模型作為磁流變阻尼器模型，根據自行火炮實際行駛的路面狀況在Simulink中構建路面激勵作為輸入，對半主動磁流變懸架模型和混合控制器進行聯合仿真和優化控制，仿真結果表明，相較于純天棚以及純地棚控制，該控制策略有效地降低了車身的垂直加速度以及懸架動行程，提高了自行火炮的平穩性。

1 MR阻尼器正向和逆向模型的建立

1.1 正向模型

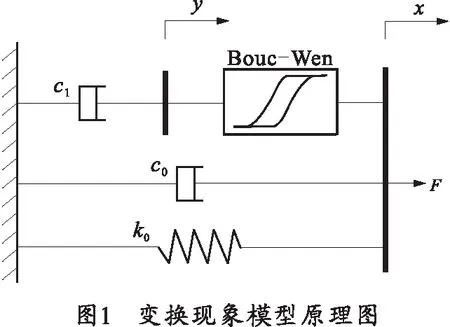
MR阻尼器的變換現象模型是通過對現象模型中各元件數量以及位置的調整并引入了歸一化的概念所得到，模型結構[11]如圖1所示，由磁滯元件、阻尼元件和彈性元件所組成。模型表達式如下：

(1)

(2)

(3)

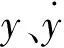
模型中各參數值[12]分別如下：n=1，ρ=9.35，k0=0.56 N/mm，f0=-14.24 N，σ=0.99 mm-1，其中c0、c1、α與電流I滿足一定的函數關系：

(4)

c1=64I+48.4,

(5)

α=-305.1I2+1 277I+43.9.

(6)

1.2 逆向模型

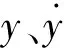
(7)

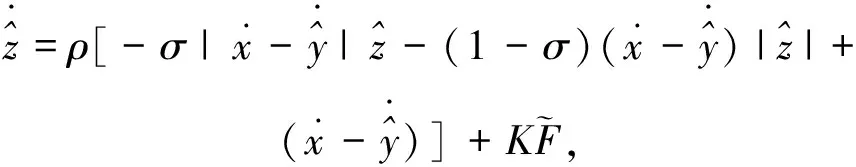
(8)

(9)

(10)

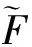
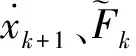
在Simulink中建立狀態觀測器、磁流變阻尼器逆向及正向模型，驗證所建逆模型的有效性。其中期望的阻尼力由正向模型產生，控制電流Ik+1由前一時刻的電流Ik經狀態觀測器、逆向模型所輸出，將Ik+1，xk+1輸入到正向模型中即可得到實際的阻尼力。仿真結果如圖2所示。其中位移取頻率0～5 Hz，幅值±15 mm的高斯白噪聲信號，電流取頻率0～10 Hz，幅值0～2 A的高斯白噪聲信號。

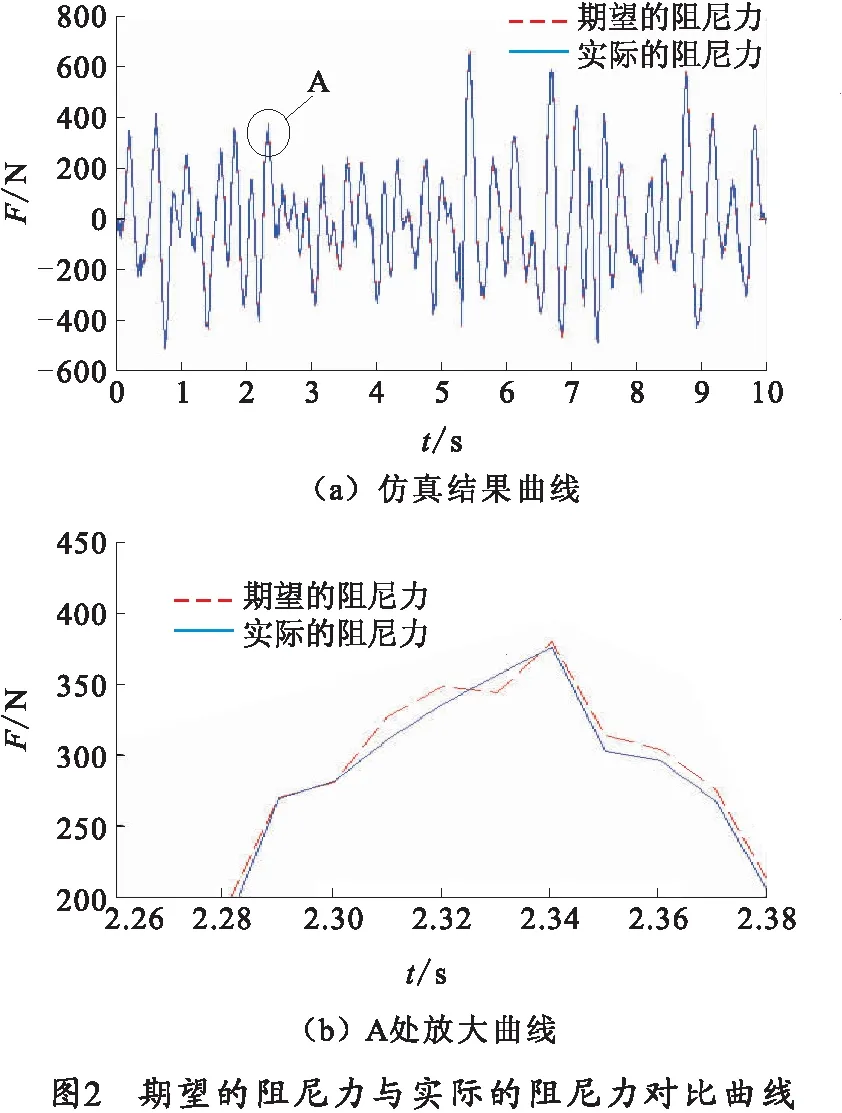
從圖2可以看出，實際的阻尼力曲線和理想的阻尼力曲線在局部上存在著較小的跟蹤誤差。但從整體上來說，所建立的逆模型對控制電流的預測精度較高，實際阻尼力能夠對理想阻尼力進行很好地逼近，可以滿足控制系統的要求，驗證了所建逆模型的有效性。

2 半主動磁流變阻尼器懸架模型

2.1 路面激勵輸入

自行火炮在鋪裝路面或越野路面上機動行駛過程中，路面不平度是車輛系統受迫振動的主要激勵。在描述路面平整程度時，通常將路面相對基準面的高度q沿道路走向長度變化q(I)稱之為路面不平度函數。根據ISO和我國GB 7031標準中規定，路面空間功率譜密度為[14]

(11)

式中：n為空間頻率；n0為參考空間頻率，取0.1 m-1；下限空間頻率nl為0.011 m-1；上限空間頻率nu為2.83 m-1.

考慮到自行火炮路面條件復雜，選擇D級路面并采用濾波白噪聲的方法生成路面激勵，路面輸入為

(12)

式中：f0為濾波器的下限截止頻率，取0.063 Hz；v為速度，取30 km/h.

2.2 半主動懸架動力學模型

輪式自行火炮懸掛系統多采用螺旋彈簧+液壓筒式減振器的獨立懸掛系統，其中把液壓筒式減振器替換為磁流變阻尼器即構成了磁流變半主動懸架系統。

針對輪式自行火炮，由路面激勵引起的車體振動會使炮塔、火炮和瞄準鏡一起振動，進而影響火炮的射擊精度。振動形式主要分為垂直振動和俯仰振動，由于現代火炮一般都具有火炮穩定器，可以對車體的俯仰角度進行調節，因此對火炮懸架一般主要考慮其垂直方向的振動。通常可以把懸架系統簡化為二自由度1/4車輛模型[15]。磁流變半主動懸架1/4車輛模型如圖3所示。

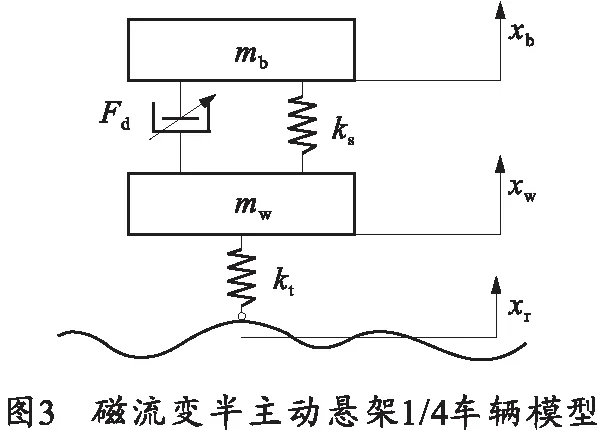
圖3中mb為簧載質量；mw為非簧載質量；ks為懸架彈簧剛度；kt為輪胎剛度；Fd為可調阻尼力。

由圖3可列出半主動懸架的運動微分方程：

(13)

(14)

2.3 懸架評價指標

自行火炮懸架系統控制的目標是使自行火炮能同時獲得良好的操縱穩定性和平順性，反映在物理上即限制懸掛系統的動行程以防止導向機構撞擊限位器，同時盡可能降低車身的垂直加速度。而就輪式自行火炮，當車輪動載較大時會導致車輪變形增大，影響車輛行駛的穩定性，因此一般也會提出車輪動載的要求。

筆者選用車身垂直加速度、懸架動行程、輪胎動載荷作為輪式自行火炮懸架的評價指標。車身垂直加速度反映了車輛行駛的平順性，一般用均方根值的大小進行說明。懸架動行程反映了成員乘坐的舒適性。輪胎動載荷影響車輛的操縱穩定性，由于輪胎動載荷系數固定不變，所以通常也采用輪胎動變形作為衡量操縱穩定性的評價指標。

3 基于粒子群優化的混合控制策略

天棚阻尼控制、地棚阻尼控制都是半主動懸架經典的控制策略。由于二者均只能就車輛行駛的某一方面性能進行改善，故Ahmadian等[16]通過引入權衡系數將天棚、地棚控制結合起來提出了半主動懸架的混合控制。理想的混合控制模型如圖4所示，其中csky為天棚阻尼系數，cgrd為地棚阻尼系數，cp為懸架減震器的固有阻尼。

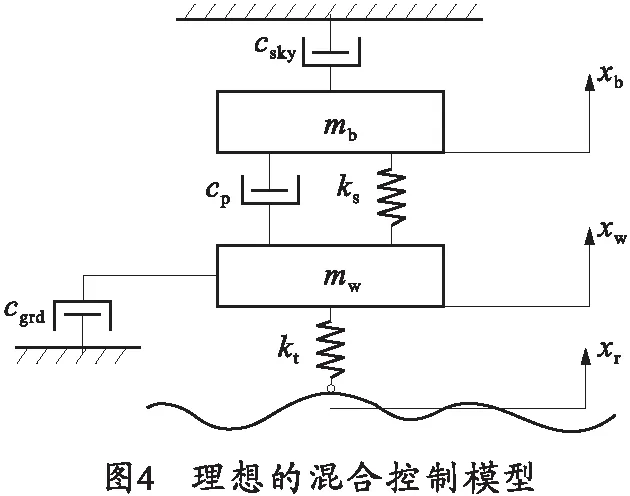
當理想的混合控制采用半主動進行實現時,滿足如下的控制規律：

(15)

(16)

Fd′=αFsky+(1-α)Fgrd,

(17)

式中,α為權衡系數，當α取1時為純天棚阻尼控制；α取0時為純地棚阻尼控制。

為了使混合控制器的輸出滿足MR阻尼器的應用范圍，需要建立相應的調節器。根據當前時刻的活塞相對位移以及相對速度可獲得阻尼器所能提供的最大阻尼力Fmax和最小阻尼力Fmin.調節后的期望阻尼力Fdes與Fd′、Fmax和Fmin滿足如下的關系表達式：

(18)

根據式(15)～(18)可以看出，權衡系數α、天棚阻尼系數csky、地棚阻尼系數cgrd為混合控制器的未知參數，大量研究表明，如果3個參數匹配得當，可使懸架處于良好的工作狀態。筆者將采用粒子群算法對3個參數進行優化。整個優化流程如下：PSO程序產生初始粒子群并將該粒子群中的粒子依次賦給混合控制器的3個參數α、csky、cgrd，然后運行控制系統的Simulink模型，得到該組參數對應的性能指標，該性能指標傳遞到PSO中作為該粒子的適應值，記錄下每個粒子及整個種群的最優位置，更新粒子，循環進行直到滿足一定的迭代次數退出算法。粒子在搜索空間中的速度和位置更新公式如下所示：

vt+1=wvt+c1r1(Pt-xt)+c2r2(Gt-xt)，

(19)

xt+1=xt+vt+1，

(20)

式中:x為粒子的位置；v為粒子的速度；w為慣性因子；c1、c2為加速常數；r1、r2為[0,1]區間的隨機數；Pt是粒子迄今為止搜索到的最優位置；Gt是整個粒子群迄今為止搜索到的最優位置。

選擇初始種群為20，最大迭代次數為100進行粒子群優化。慣性權重w采用線性遞減的方法，既保證了在搜索初期具有較大的搜索范圍，后期又加強了局部尋優，如下所示：

(21)

式中:wmax為初始權重，取1.4；wmin為最終權重，取0.4；tmax為最大迭代次數100;t為當前迭代次數。

粒子群優化的適應度函數設置為

(22)

式中，系數q1、q2、q3的設置是為了把各評價指標統一到相同的數量級上，筆者取q1為1，q2為45 000，q3為300 000.

4 聯合仿真

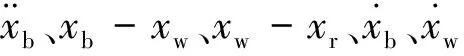
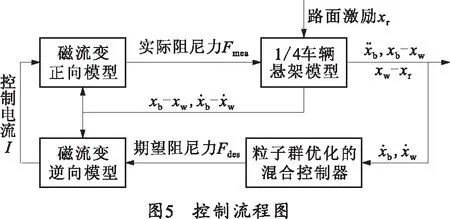
在Simulink中搭建聯合仿真平臺，如圖6所示，在聯合仿真的過程中，采用粒子群算法對混合控制器的3個參數進行尋優，整個尋優的過程如圖7所示，可看到種群在第25代后不發生進化，說明最優值在第25代取得。各參數的最優值分別為α=0.756，csky=29 437 N·s/m，cgrd=20 312 N·s/m.

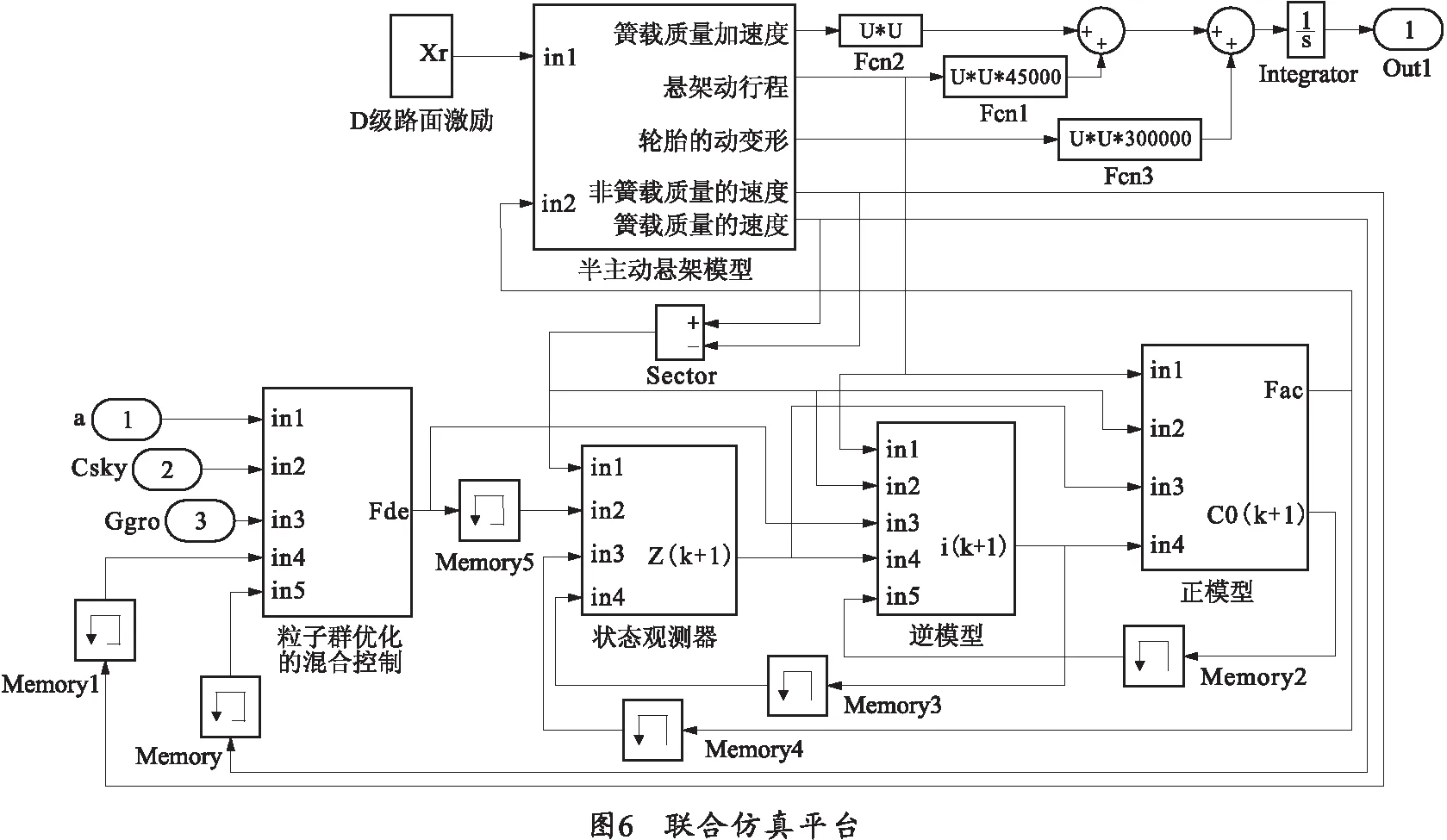
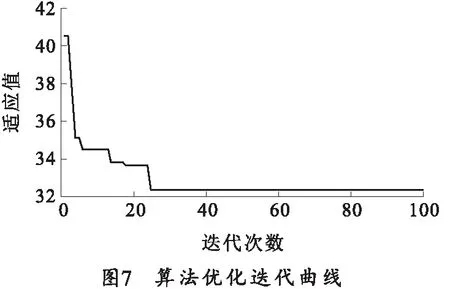
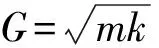
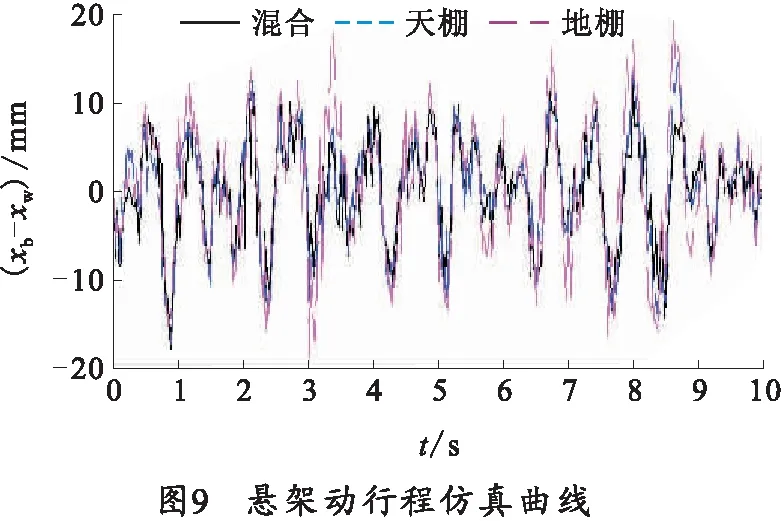
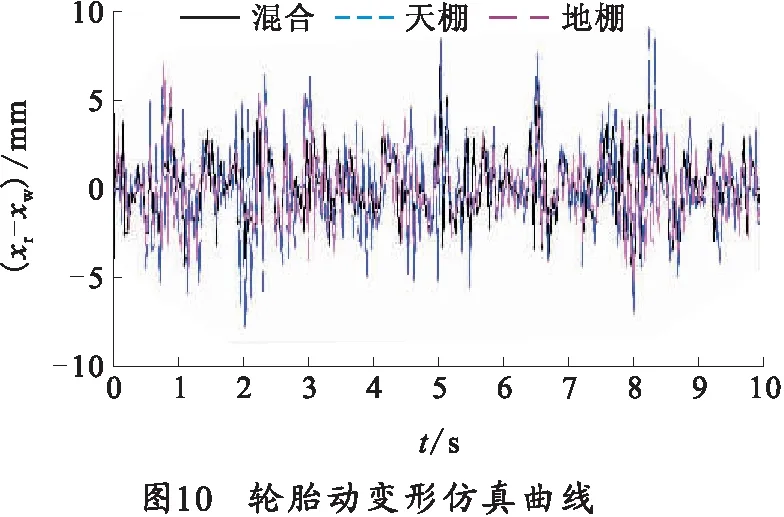
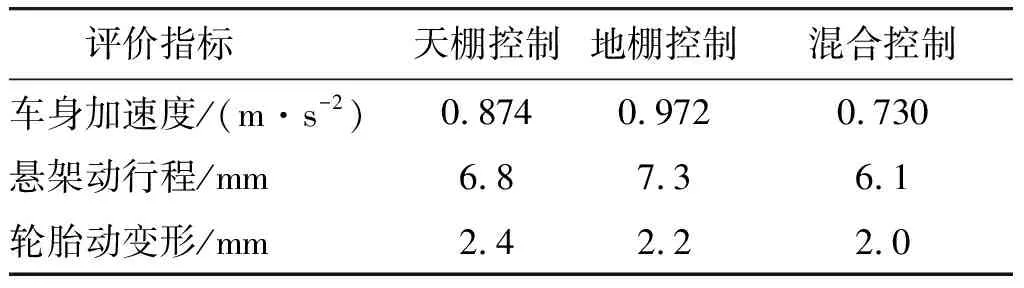
表1 仿真結果

5 結束語

筆者針對自行火炮行進間減振這一問題，提出了基于磁流變阻尼器的混合控制策略，在仿真平臺中構建了模型刻畫精度較高的磁流變變換現象模型，結合半主動懸架模型和混合控制器進行聯合仿真，仿真結果表明，筆者提出的控制策略可以較好地兼顧自行火炮行駛的平順性和操縱穩定性，一定程度上也提高了自行火炮行進間的射擊精度。