“Ⅳ型” 激波干擾中流-熱-固耦合問題一體化計算分析

李佳偉，王江峰，楊天鵬，李龍飛，王丁

南京航空航天大學 非定常空氣動力學與流動控制工業和信息化部重點實驗室，南京 210016

吸氣式高超聲速飛行器的研究已成為當今世界航空航天發展的一個重要方向，但同時，與之伴隨的氣動熱防護問題也成為一項亟待解決的重要技術難題[1]。如圖1所示，以超燃沖壓發動機為動力的高速飛行器在大氣層中以高馬赫數飛行時，將面臨十分嚴峻的氣動熱力學環境。特別是，其前體產生的激波系與進氣道唇緣弓形激波發生干擾，形成激波-邊界層、激波-剪切層、激波-激波相互作用等非線性物理現象[2]。激波干擾產生的復雜流場波系結構，在高速飛行器表面產生局部高溫高壓載荷，給飛行器的性能和結構帶來極大安全隱患，同時也給高超聲速飛行器熱防護問題提出了很大挑戰。

Edney[3]根據激波干擾點的位置，將激波干擾分為6種類型(Ⅰ～Ⅵ型)，其中Ⅳ型干擾形成超聲速射流沖擊壁面，產生極大的壓強和熱流[4-5]，對飛行器安全影響最大，因此備受關注，也是本文主要研究內容。另外，高速飛行器外部流場的氣動加熱與熱防護結構內的熱傳導相互作用不可分割，因此要準確預測“Ⅳ”型激波干擾下飛行器的氣動熱環境，必須考慮氣動加熱與結構傳熱的相互耦合作用[6]。

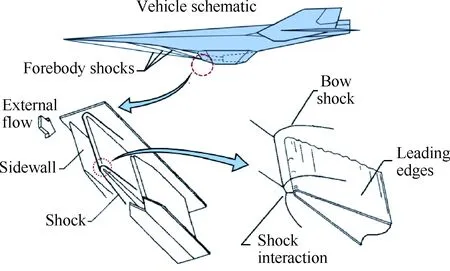
圖1 前體-進氣道激波干擾示意圖
Fig.1 Schematic diagram of forebody-inlet shock wave interference

目前，國內外學者針對高超聲速流-固-熱多場耦合問題已經開展了大量研究工作。例如，Thornton和Dechaumphai[7]基于有限元方法提出了一種雙向耦合計算方法來求解不銹鋼平板在高超聲速流動下的氣動加熱傳熱與變形問題，計算結果證明了多場耦合計算的重要性。Kazemi-Kamyab等[8]在分區雙向耦合的基礎上發展了一種強耦合迭代計算方法，采用高階隱式時間迭代方法來求解流場與結構非穩態共軛傳熱計算問題，從而提高時域上的計算精度。Chen等[9]發展了一種高超聲速流場-熱-結構耦合分析平臺(HyCCD)，分析了高超聲速前緣在高溫高壓條件下的熱力學行為，同時引入自適應時間步長計算方法，提高計算效率。Qin等[10]利用MPCCI多平臺耦合計算軟件將FLUENT與ABAQUS兩種商用軟件進行聯合使用，計算模擬了高超聲速條件鈍體外形在不同支桿外形下流-熱-固多場耦合特性，分析了不同外形支桿對高超聲速鈍頭體的減阻防熱效果。Zhao等[11]依據結構熱響應特征時間較小的特點，發展了一種新的多物理場松耦合計算方法，數值模擬了馬赫數為6.47下三維非定常圓管流-熱-固耦合算例，得到的熱壁熱流、冷壁熱流以及圓管溫度與試驗值吻合。Zhang等[12]基于自動控制理論發展了一種基于PID(Proportional-Integral-Differential)控制的自適應時間步長的松耦合高效計算方法，用于計算分析高超聲速流中的共軛傳熱問題。

然而需要指出的是，上述計算方法都歸屬于多場分區耦合迭代計算方法，即將流場和固體結構獨立分開建模，基于“準穩態耦合”策略，在耦合交界面進行數據傳遞與交換，同時在時間域上進行耦合交替迭代。后來，NASA蘭利研究中心的Wieting等[13]認為多物理場分區耦合計算方法將連續的物理場進行分割建模，耦合界面需要額外的數據插值方法和交換策略，這種計算方法雖然較容易實現，但無法準確模擬流-熱-固多物理場耦合特性。李鵬飛和吳頌平[14]在對高速飛機機身結構進行氣動加熱與結構傳熱的耦合數值計算分析后，認為為了準確分析熱壁對傳熱計算的影響，很有必要開展氣動加熱與結構傳熱一體化數值計算方法研究。姜貴慶等[15]為了滿足多場耦合計算問題中連續變化的物理條件，提出了基于有限元方法的流-熱-固一體化計算方法，流場與結構溫度傳熱計算采用統一網格和計算程序，計算結果表明一體化計算可以保證熱結構的計算精度。

本文基于多物理場連續變化的物理條件，發展了一種高超聲速流-熱-固一體化計算方法。該方法基于有限體積法，將高超聲速流場與結構溫度場統一到同一控制方程中，并進行統一離散與統一求解，避開了傳統分區耦合方法所需的數據傳遞策略。同時，提出一種新的雙溫阻模型以保證交界面上物理場的連續性。選取典型高超聲速繞流二維鈍體算例驗證本文方法的可靠性與正確性，最后采用本文計算方法對高超聲速“Ⅳ型”激波干擾開展流-熱-固一體化計算與分析研究。

1 一體化數值計算方法

1.1 一體化控制方程及求解方法

首先推導一體化控制方程。固體結構傳熱控制方程積分形式(不含熱源，暫忽略熱輻射換熱)可寫為

(1)

對于結構外部流場計算，采用積分形式的可壓縮Navier-Stokes方程作為控制方程，方程形式與式(1)相似，因此，流場計算方程與固體結構傳熱方程可寫成如下統一控制方程：

(2)

式中：W為守恒量；Fc為對流通量；Fv為黏性通量。W、Fc、Fv的表達式為

上述控制方程用于流場計算時，u、v、w分別為控制體3個方向的速度；V=nxu+nyv+nzw為面法向速度，其中nx、ny、nz為面法矢分量；τij為應力張量分量；H為總焓，H=E+p/ρ，其中E為流體控制體總能,p為壓力。另外控制方程滿足理想氣體狀態方程p=ρRT，R為理想氣體常數。對于固體結構傳熱計算時，結構無變形滿足u=v=w=0，式(2)中對流通量項Fc=0，黏性通量項中，Θx=k?T/?x，Θy=k?T/?y，Θz=k?T/?z;E=CsT為固體結構單元控制體內能。

采用有限體積法對上述一體化控制方程進行離散求解。其中采用AUSM+[16]迎風格式求解對流通量項，同時基于Venkatakrishnan[17]限制器采用MUSCL[18]插值方法進行線性重構，以實現二階精度計算。采用二階中心差分格式計算黏性通量項。時間推進采用LU-SGS(Lower-Upper Symmetric Gauss-Seidel)隱式時間迭代計算方法，其中流場當地時間步長計算公式為

(3)

式中:Ncfl為CFL數；Λc和Λv分別為控制體I單元所有邊界的對流譜半徑和黏性譜半徑的累加；ΩI為第I個單元的體積；C為常數。

針對結構傳熱方程的計算時間步長，需要注意的是，結構傳熱過程中產生的熱脈沖需要限制在當地固體結構單元中，才能保證計算的穩定性。因此，結構傳熱方程當地時間步長計算公式為

(4)

式中：δx為單元最小邊長;α為熱擴散率。

另外，為保證壁面熱流計算的準確性，需要選取合適的湍流模型。對多種湍流模型進行對比分析后，確定選取Menter[19]提出的SST(Shear Stress Transport)k-ω兩方程湍流模型，該模型不需要阻尼函數，能較好計算邊界層近壁面熱通量。

1.2 流-固耦合界面參數定義

由于外部流場與固體結構熱力學特性差異較大，本文一體化計算方法為了保證流-固耦合界面熱通量與溫度的連續性，需要對交界面的熱力學參數進行特別計算。

圖2給出了流-固交界面左右單元意圖，Ωf和Ωs分別表示流體單元(左邊)和固體結構單元(右邊)。耦合界面的溫度計算式為

(5)

式中：下標l、r代表耦合界面左、右單元。

(6)

式中:Llr為左右單元中心之間的距離;rlr為單位向量。

值得注意的是，流-固交界面的熱傳導系數的計算對一體化傳熱計算起到關鍵作用。固體結構內部導熱系數較大，交界面的熱傳導系數采用簡單加權平均會對計算產生很大誤差，為了提高計算的準確性與合理性，本文提出了一種雙-熱阻抗模型用于計算交界面熱傳導系數。其中熱阻抗表征的物理意義為熱量在介質中傳導時所遇到的阻力，其定義為

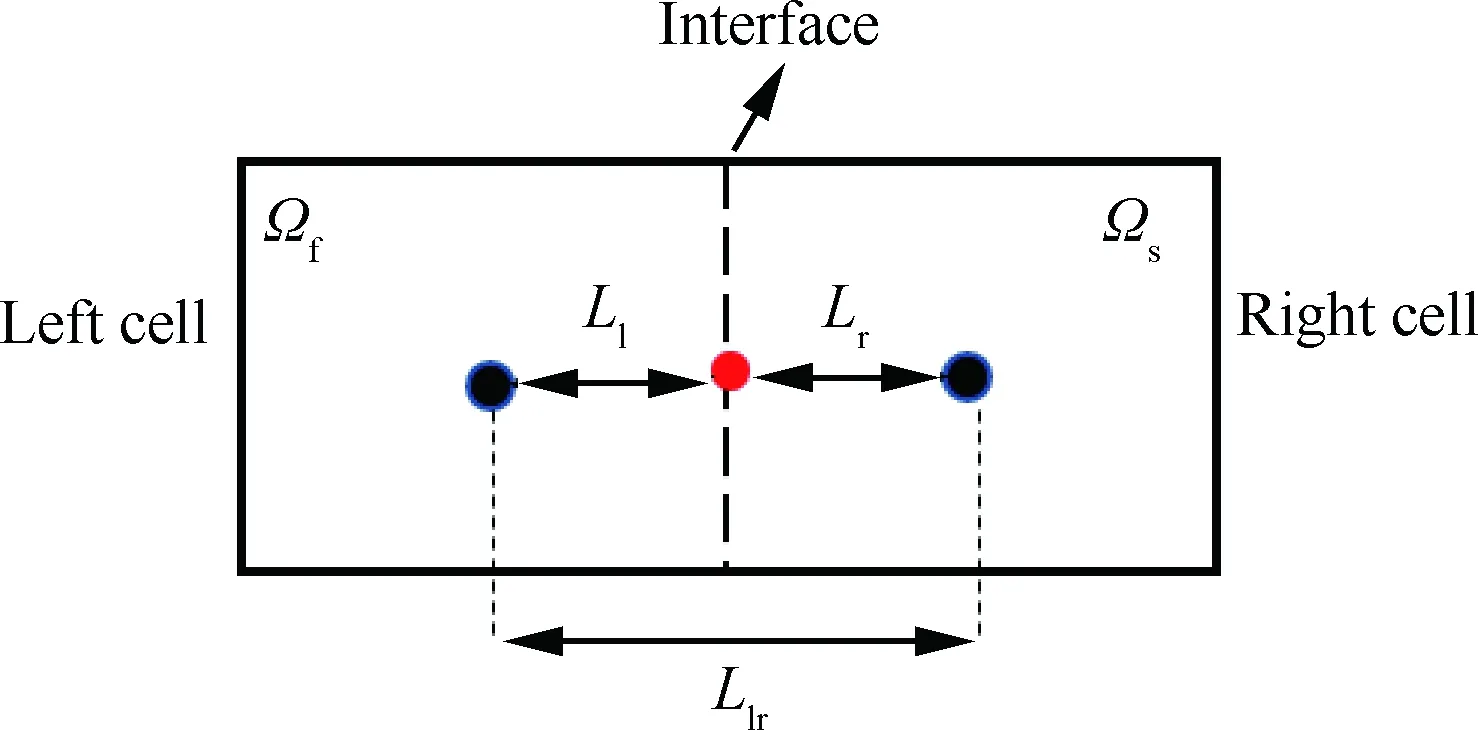
圖2 流-固交界面左右單元意圖
Fig.2 Schematic diagram of left and right cells at fluid-solid interface

(7)

式中:L為熱通量傳導的距離;A為熱量傳導的截面面積。因此，可以得到交界面的熱阻關系式為

Rt,bnd=Rt,l+Rt,r

(8)

其中：Rt,l和Rt,r分別為交界面左右單元的熱阻。將式(7)代入式(8)中，得到

(9)

因此，可得交界面當量導熱系數k為

(10)

1.3 非定常時間步長自適應計算方法

為了提高非定常計算效率，本文非定常計算中，真實物理時間步長采用于經典PID控制器[22]調節的自適應控制算法進行實時計算，以取代傳統固定時間步長，偽時間步長選取當地時間步長。

圖3為自適應時間步長PID控制器示意圖，整個自適應控制器由處理器和控制器2個部分組成。自適應控制基本原理為：處理器將時間步長Δt作為輸入控制參數，進行數值迭代輸出誤差值e；控制器根據輸出誤差值e和給定輸入的容錯值tol進行反饋控制，計算合適的新時間步長Δt。

通過PID控制器得到的真實物理時間步長Δt計算為

(11)

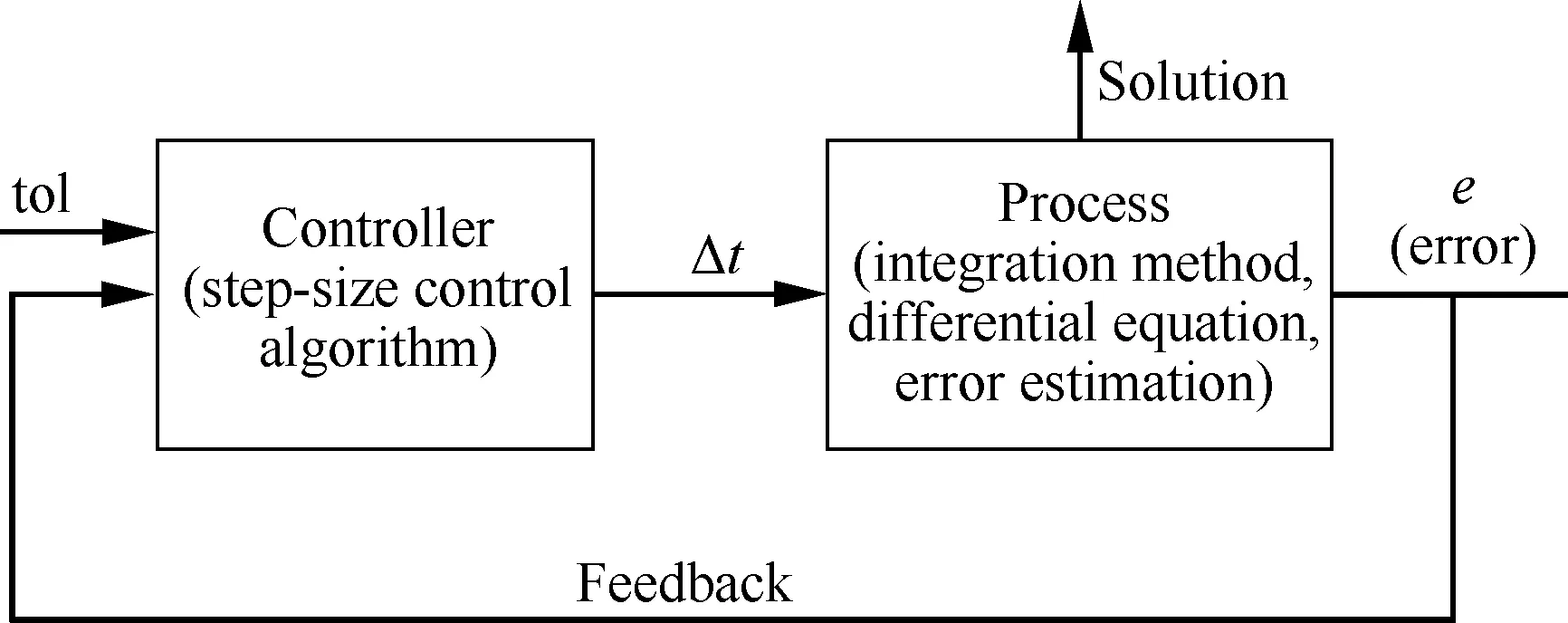
圖3 時間步長PID控制器示意圖
Fig.3 Schematic diagram of PID control system in time step-size

式中:n為計算迭代時間步；kP、kI、kD為PID控制器參數,分別取值為kP=0.075，kI=0.175,kD=0.015；en為溫度誤差值，其計算式為

(12)

其中:tol為給定值，本文給定tol=1.0。

為了保證PID控制器的穩定性和計算迭代的收斂性，需要對時間步長的大小和增長率進行一定約束：

Δtmin≤Δtn≤Δtmax

(13)

(14)

(15)

式中：Δtmin和Δtmax分別為設定的最小和最大的非定常計算時間步;αref為時間步長控制率，一般0.2<αref<0.4，理想取值αref≈0.2;α的表達為

(16)

2 驗證算例

2.1 計算模型及網格

選取經典不銹鋼圓管前緣氣動加熱與傳熱試驗[23]來驗證一體化計算方法的準確性，該算例已多次被用于驗證高超聲速流-熱-固多場耦合計算。圓管外徑尺寸為Rout=38.1 mm,內徑尺寸為Rin=25.4 mm,結構材料為不銹鋼，表1給出了不銹鋼材料熱性能參數[24]。

圖4給出了驗證算例的計算網格和邊界條件。流場與結構傳熱計算采用統一網格，圖中綠色部分為流場計算網格，紅色部分為圓管結構傳熱計算網格。為了更好捕捉流場激波結構，流場網格在激波位置附近進行加密。圓管的熱邊界條件為：兩端為絕熱壁，內壁為等溫壁，初始溫度為294.4 K。表2給出了初始來流計算條件，Ma∞、T∞、p∞、Re∞分別為來流馬赫數、溫度、壓力和單位雷諾數。

表1 不銹鋼材料熱力學參數[24]Table 1 Material thermal properties of stainless steel[24]

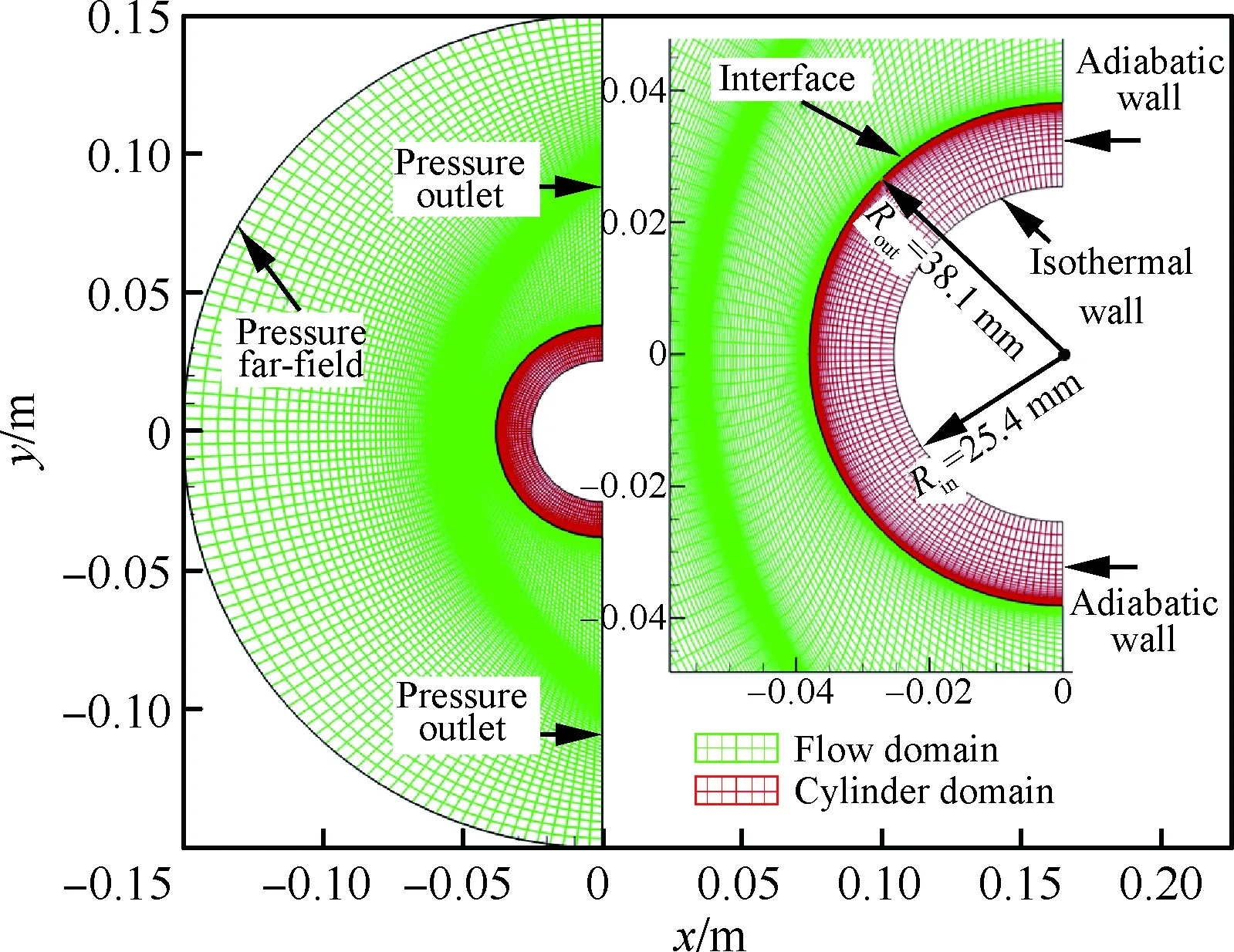
圖4 計算網格與邊界條件
Fig.4 Computational grids and boundary conditions

表2 初始來流條件Table 2 Initial freestream condition

由于近壁面溫度梯度的準確計算直接依賴于近壁面網格單元的尺寸，因此為了更加準確計算壁面熱流，采用當地網格雷諾數Relocal=ρUΔh/μ[25]來確定物面法向第1層網格的合適高度，其中ρ、U、μ為流體密度、速度和動力黏性系數，Δh為網格高度。文獻[25]指出：Relocal應不大于3才能保證壁面熱流計算結果的準確性。因此，流場網格在壁面法向第1層高度取1×10-6m，當地網格雷諾數約為1.21，滿足網格計算要求。同時，為保證熱流計算的連續性，圓管網格在流固交界面處第1層高度也取1×10-6m。

2.2 計算結果與分析

為了與參考文獻和試驗結果更好進行對比，采用提出的一體化計算方法對不銹鋼材質圓管開展高超聲速氣動加熱與結構傳熱非定常數值模擬，初始真實時間步長取Δt0=1×10-4s。

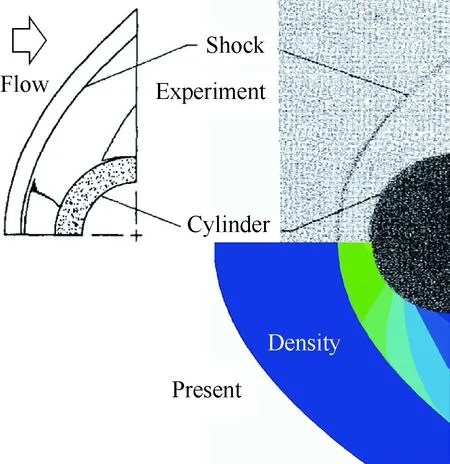
圖5 密度等值線圖與試驗紋影圖[26]對比
Fig.5 Comparison of predicted density contours with experimental schlieren photograph[26]

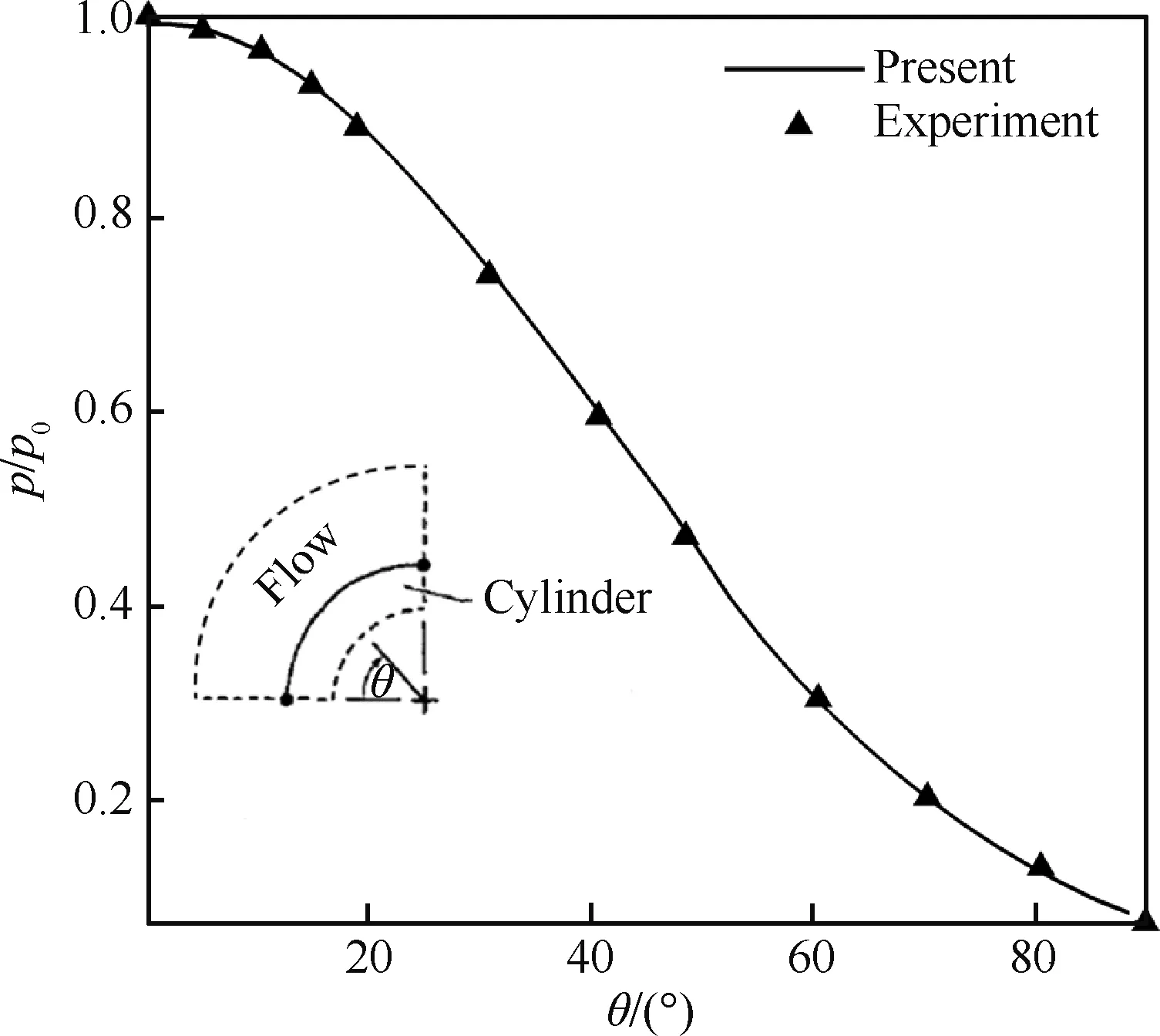
圖6 圓管表面壓力分布對比
Fig.6 Comparison of surface pressure distributions on cylinder

圖5直觀地給出了初始時刻計算得到的圓管外部流場的密度云圖與風洞試驗紋影圖[26]的對比結果，從圖中可以看出計算預測的激波位置和流場結構與試驗結果吻合較好，說明本算例暫不考慮高溫空氣化學非平衡效應是合理的。另外，圖6為歸一化后的圓管表面壓力(p/p0，p0為駐點壓力)分布與試驗值的對比，從圖中可以看出壓力沿圓管的分布和試驗值吻合較好。

圖7給出了初始時刻(t=0 s)圓管外表面歸一化熱流(q/q0,q0為駐點熱流)分布與風洞試驗值的對比曲線，結果顯示計算預測的熱流分布與試驗結果保持一致。另外，t=0 s時刻，圓管表面駐點處熱流值最大，本文方法計算得到的駐點處熱流值為49.21×104W/m2，與采用Fay-Riddell[27]工程經驗公式計算得到的駐點熱流值48.27×104W/m2以及采用黏性激波層[28]計算方法得到的47.02×104W/m2基本一致。但是與風洞試驗值67.0×104W/m2差別較大，這是由于數值計算中暫未考慮風洞試驗中來流湍流度對氣動加熱熱流的影響所導致。

圖7t=0 s圓管表面熱流分布對比
Fig.7 Comparison of surface heat flux distributions on cylinder att=0 s

圖8展示了不同時刻下流場與圓管結構沿中心線(y=0 m)溫度變化曲線。從曲線圖可以看出，高速自由來流在圓管前端產生脫體弓形激波，溫度從初始的241.5 K急劇躍升到2 162 K，與文獻[12]計算結果2 163.7 K基本吻合。另外，本文計算得到的弓形激波的位置約在-54.5 mm處，與激波經驗公式[29]計算得到的-54.4 mm基本吻合，說明了本文計算方法可以較準確捕捉高速流場激波位置。初始時刻，在圓管駐點處，流場溫度急劇降低至294.4 K，在駐點區域會產生一個明顯的薄熱邊界層，其厚度約為激波層厚度的2.9%。從曲線圖可以看出，在薄熱邊界層中流場溫度變化非常明顯，產生很大溫度梯度，因此在該區域會產生很高的壁面熱流。另外，圖8也給出了圓管溫度沿中心線隨時間變化的放大曲線圖，可以觀察到隨著時間的推移，熱量逐漸傳入不銹鋼圓管內部，圓管溫度逐漸升高且趨勢明顯。

圖9直觀地給出了不銹鋼圓管內部溫度分布隨時間變化的云圖(t=0.1,0.5,1.0,2.0 s)。可以觀察到，隨著時間的變化，外部高速氣流產生的熱量不斷傳入圓管結構內部，圓管內部溫度逐漸升高，高溫區域也不斷擴大，駐點區域溫度始終最高且不斷升高。t=2.0 s時刻，本文計算得到駐點溫度為389.2 K，與Dechaumphai等[26]的計算結果388.8 K吻合很好，誤差在0.1%左右。

為了更加準確對比驗證本文計算結果的可靠性，圖10給出了圓管駐點溫度(T0)隨時間變化曲線與文獻[30-31]的對比結果，可以看出本文駐點溫度變化趨勢與參考文獻結果相同，t=2.0 s時，最大溫度差值約為3.9 K，計算相對誤差在0.9%以內。另外，圖中還給出了駐點溫度變化率隨時間變化曲線，可以觀察到初始時刻駐點溫度升高速度最快，溫升速度逐漸減小趨于平穩。

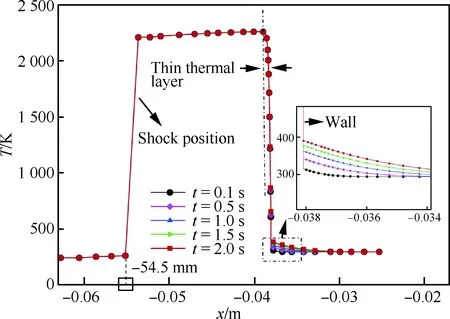
圖8 不同時刻流場與圓管沿中心線溫度分布
Fig.8 Temperature distribution along centerline within fluid and cylinder domains at different time

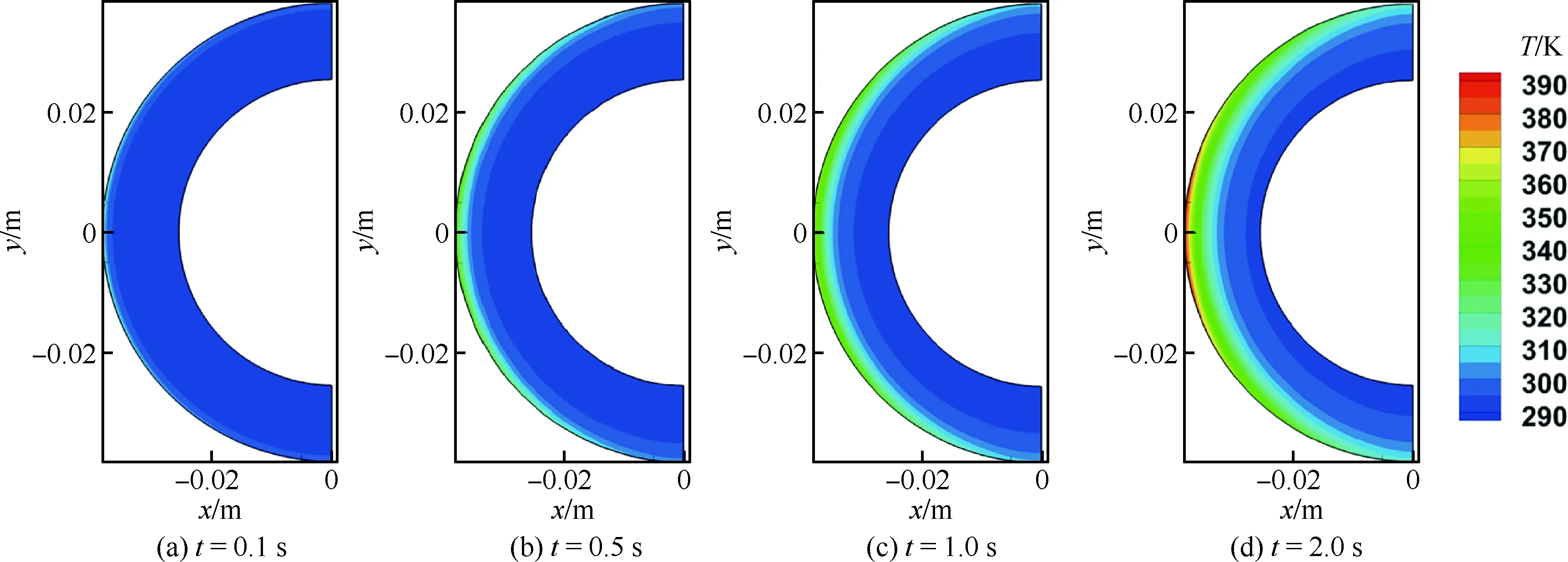
圖9 不同時刻圓管內部溫度云圖
Fig.9 Temperature contours within cylinder domain at different time

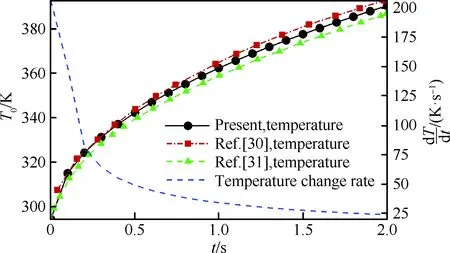
圖10 圓管駐點溫度隨時間的變化
Fig.10 Temporal variation of stagnation point temperature on cylinder

圖11為圓管駐點熱流與熱流變化率隨時間的變化曲線。隨著時間的推進，圓管壁面溫度逐漸升高，駐點區域熱邊界層內的溫度梯度逐漸減小，導致駐點熱流逐漸下降。t=2.0 s時，熱流下降約6.5%，與Dechaumphai等[26]計算的2 s內駐點熱流下降8%接近。同時從虛線可以看出駐點熱流下降速度隨時間變化也逐漸減小趨于平穩。

為了更清楚地驗證本文方法計算結果，表3給出了t=2 s時刻駐點溫度和初始時刻駐點熱流值與不同參考文獻的對比。從表中可以看出本文計算結果與各參考文獻值都吻合較好，計算誤差在允許范圍內。綜上，本算例驗證了本文流-熱-固一體化計算方法的可靠性和可行性，并可用于下文的計算與分析。

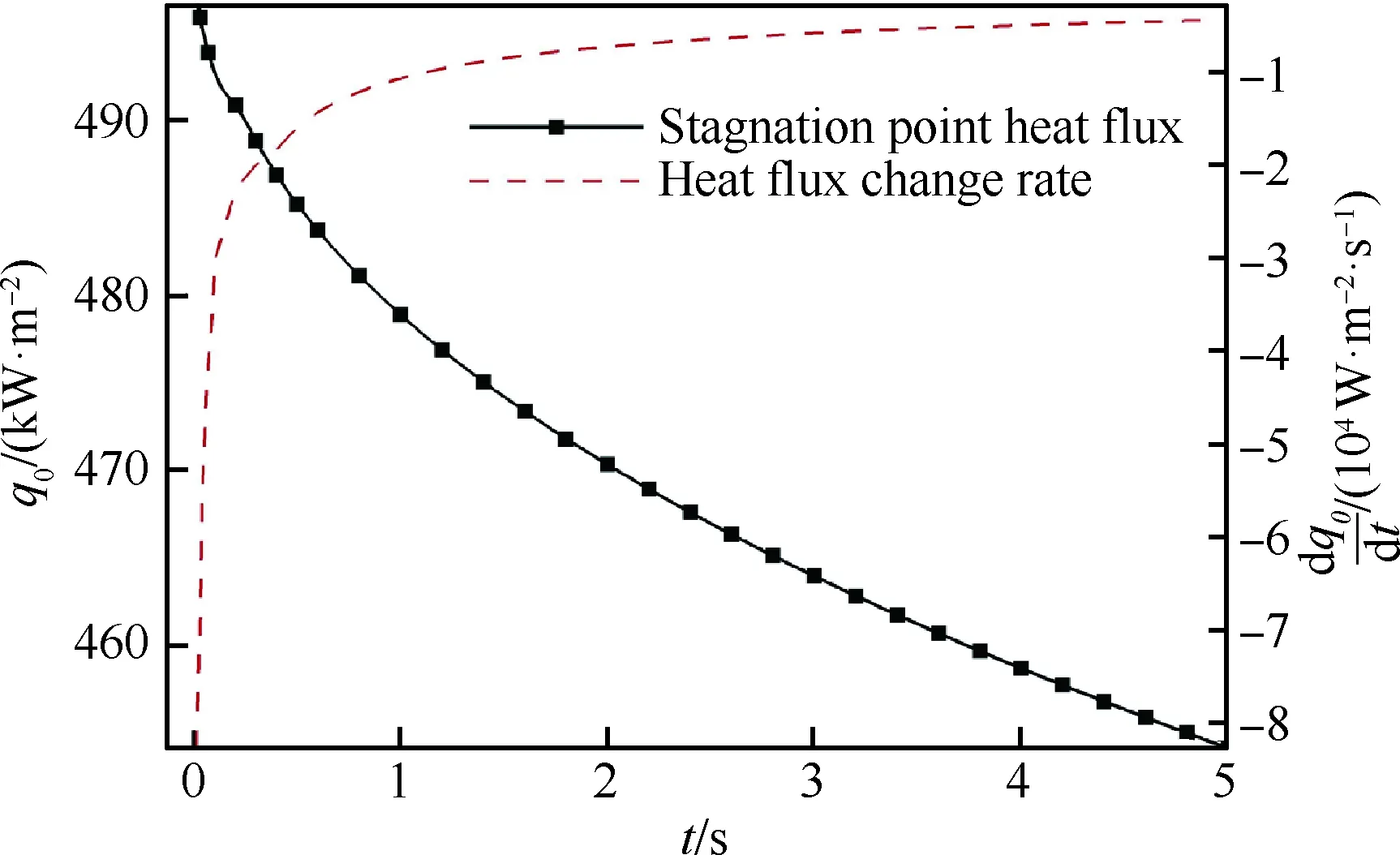
圖11 圓管駐點熱流隨時間的變化
Fig.11 Temporal variation of stagnation point heat flux on cylinder

表3 駐點溫度、熱流值對比

另外，為了對比本文一體化計算方法與傳統分區耦合計算方法的計算效率，表4列出了不同計算方法下，迭代步數與計算時間統計結果。本算例在圖形工作站(主頻 2.3 Hz，內存16 GB)上進行串行計算。

從表4中可以看出，相比傳統分區傳遞計算方法，一體化計算方法無數據交換計算過程，可以節省計算時間。采用自適應時間步長算法，可以進一步大幅度提高計算效率。

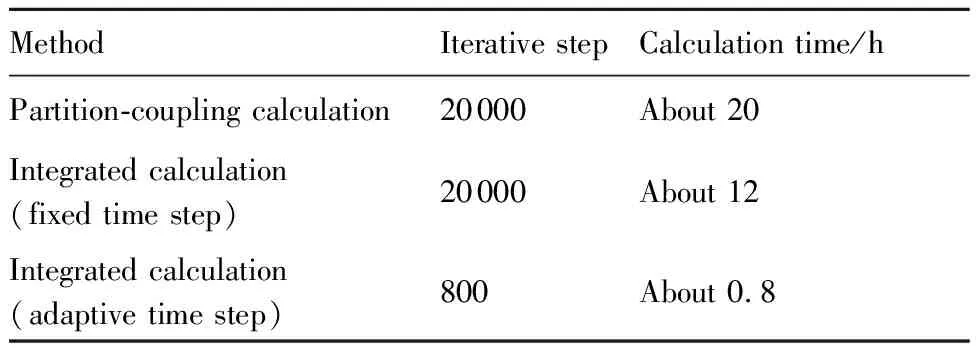
表4 迭代步數與計算時間統計結果

3 “Ⅳ型”激波干擾算例

3.1 計算模型及網格

選取與2.1節中尺寸與材質完全相同的不銹鋼圓管作為計算模型，開展高超聲速“Ⅳ型”激波干擾流-熱-固一體化計算分析研究。為了獲得高超聲速斜激波與正激波干擾產生的“Ⅳ型”激波干擾，本算例計算模型還包含了斜激波發生器，圖12給出了計算模型尺寸和激波發生器的相對位置。表5給出了初始流場來流條件，U∞為來流速度。

圖13給出了“Ⅳ型”激波干擾算例的計算網格和邊界條件。同樣，流場與結構傳熱計算采用統一四邊形網格，圖中綠色部分為流場計算網格，紅色部分為圓管結構傳熱計算網格。流場網格單元數約176 013，圓管內部結構網格單元約為49 900。流場與結構耦合交界面法向第1層網格高度都取值為1×10-6m，當地網格雷諾數約為1.98，圓管的熱邊界條件與2.1節中相同。

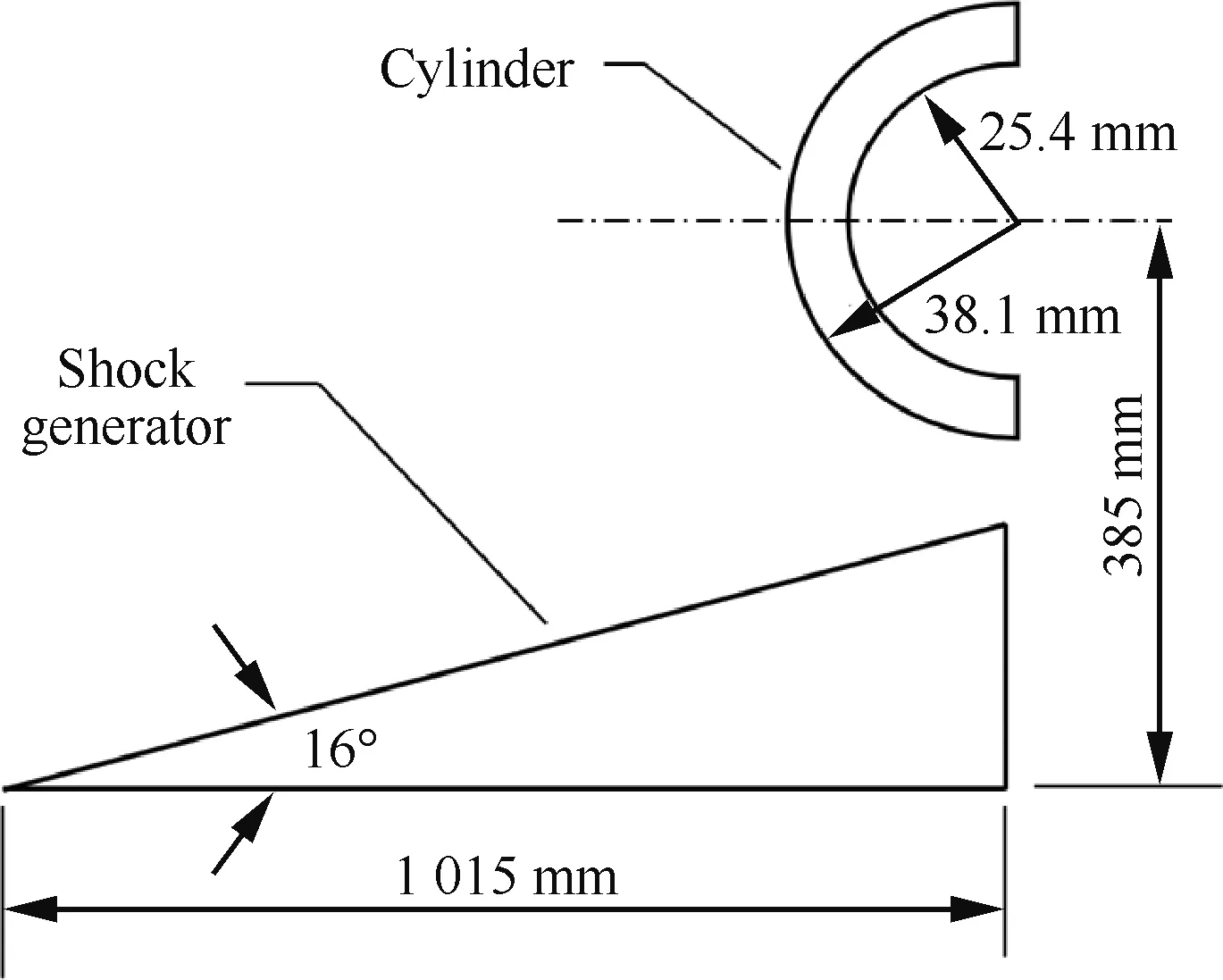
圖12 計算模型
Fig.12 Computational model

表5 “Ⅳ型”激波干擾算例的初始來流條件

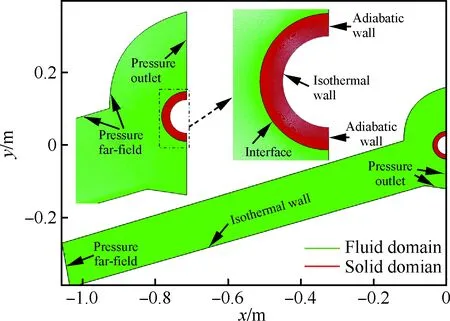
圖13 “Ⅳ型”激波干擾算例的計算網格與邊界條件
Fig.13 Computational grids and boundary conditions of “Type Ⅳ” shock wave interference case

3.2 計算結果與分析

對不銹鋼材質圓管分別開展高超聲速“Ⅳ型”激波干擾氣動加熱與結構傳熱一體化的定常與非定常數值計算，給出計算結果并進行分析。

3.2.1 定常計算結果

在進行氣動加熱與結構傳熱一體化分析之前，首先要了解高超聲速“Ⅳ型”激波干擾的流動特征。圖14顯示了圓管前緣的“Ⅳ型”激波干擾流動的穩態壓力云圖與流線結構。可以觀察到，流場具有明顯的弓形激波和透射激波的特征。計算發現當入射斜激波與圓管前方的弓形激波接近正激波的位置相交時，發生“Ⅳ型”激波干擾現象。激波發生器產生的斜激波與圓管前端產生的弓形激波干擾產生一道明顯的透射激波，將弓形激波分為上下兩個部分，且激波干擾產生的高溫高壓使得弓形脫體激波的脫體距離明顯增大。同時，上、下兩道弓形激波波后的亞聲速區中產生上、下兩道剪切層，在這兩層剪切層之間產生一股超聲速“噴流”，超聲速“噴流”沖擊圓管壁面產生一道較短的弓形滯止激波，形成一個小的滯止加熱區域，引起壁面熱流、壓力急劇上升。由此看出，“Ⅳ型”激波干擾流場結構是非常復雜的。

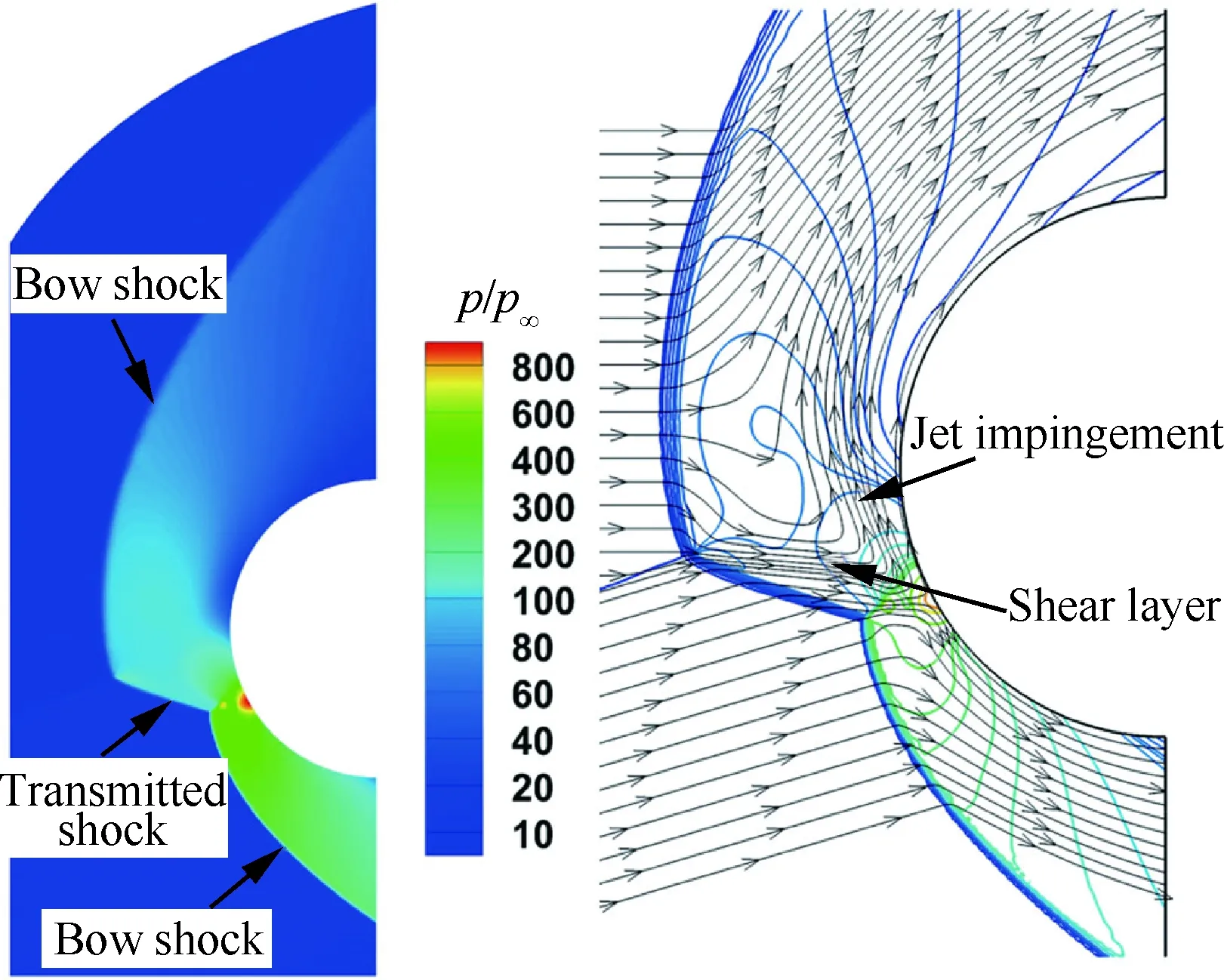
圖14 “Ⅳ型”激波干擾穩態流場結構
Fig.14 Steady flow field structure of “Type Ⅳ” shock wave interference

圖15展示了 “Ⅳ型”激波干擾流場與圓管結構內部的穩態溫度分布。自由來流經過弓形激波第1次加熱后，超聲速“噴流”產生的二次弓形滯止激波對其進一步加熱，流場溫度從初始的226.5 K急劇增加，最高溫度達到3 722.1 K。不銹鋼圓管由于外部流場的持續氣動加熱，內部結構溫度整體升高。其中，二次弓形激波在圓管壁面形成了一個局部的高溫高壓滯止加熱區域，由此導致圓管結構在該區域形成一個高溫區，最高溫度可達3 406.2 K。

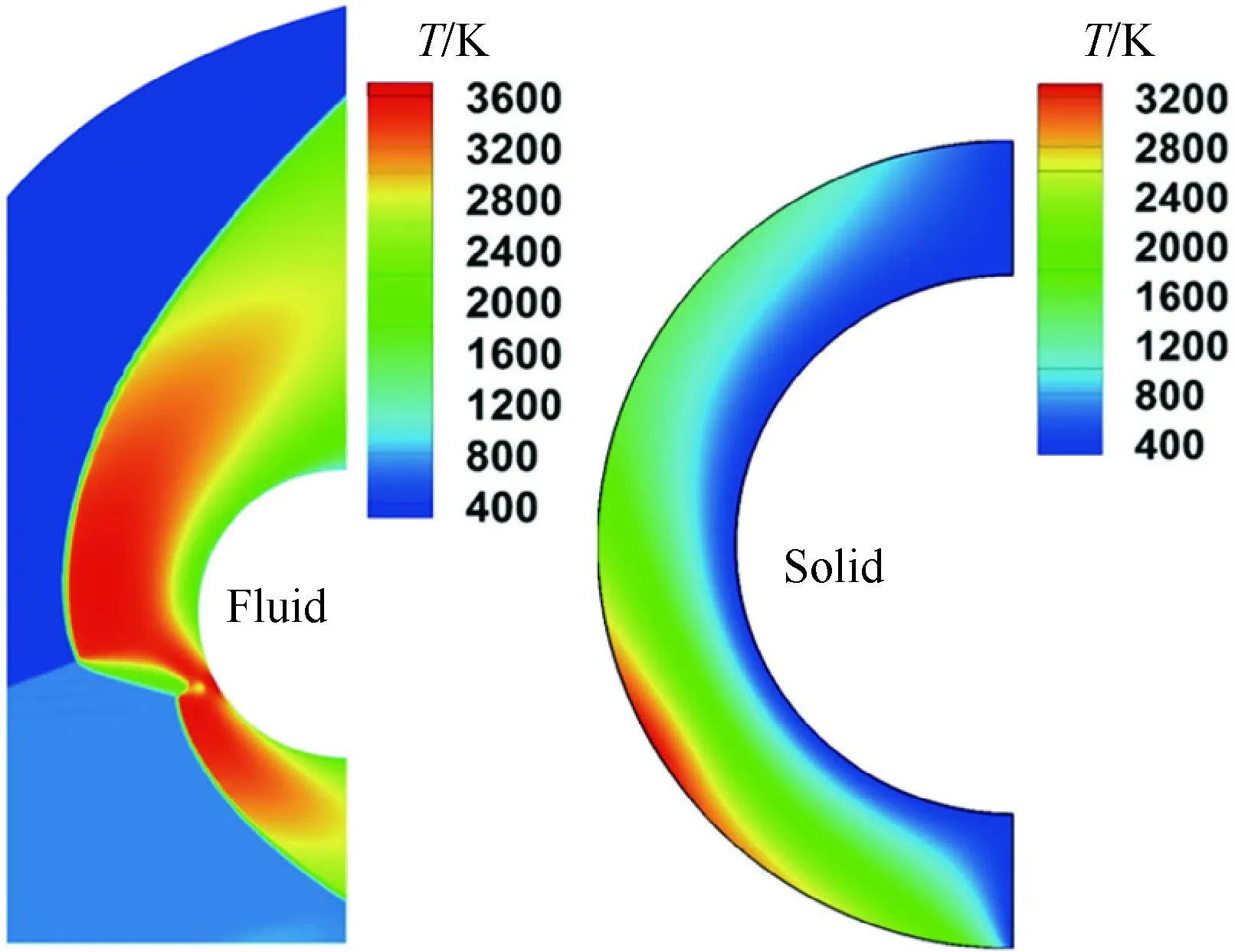
圖15 流場與圓管穩態溫度云圖
Fig.15 Steady temperature contours within fluid and cylinder domains

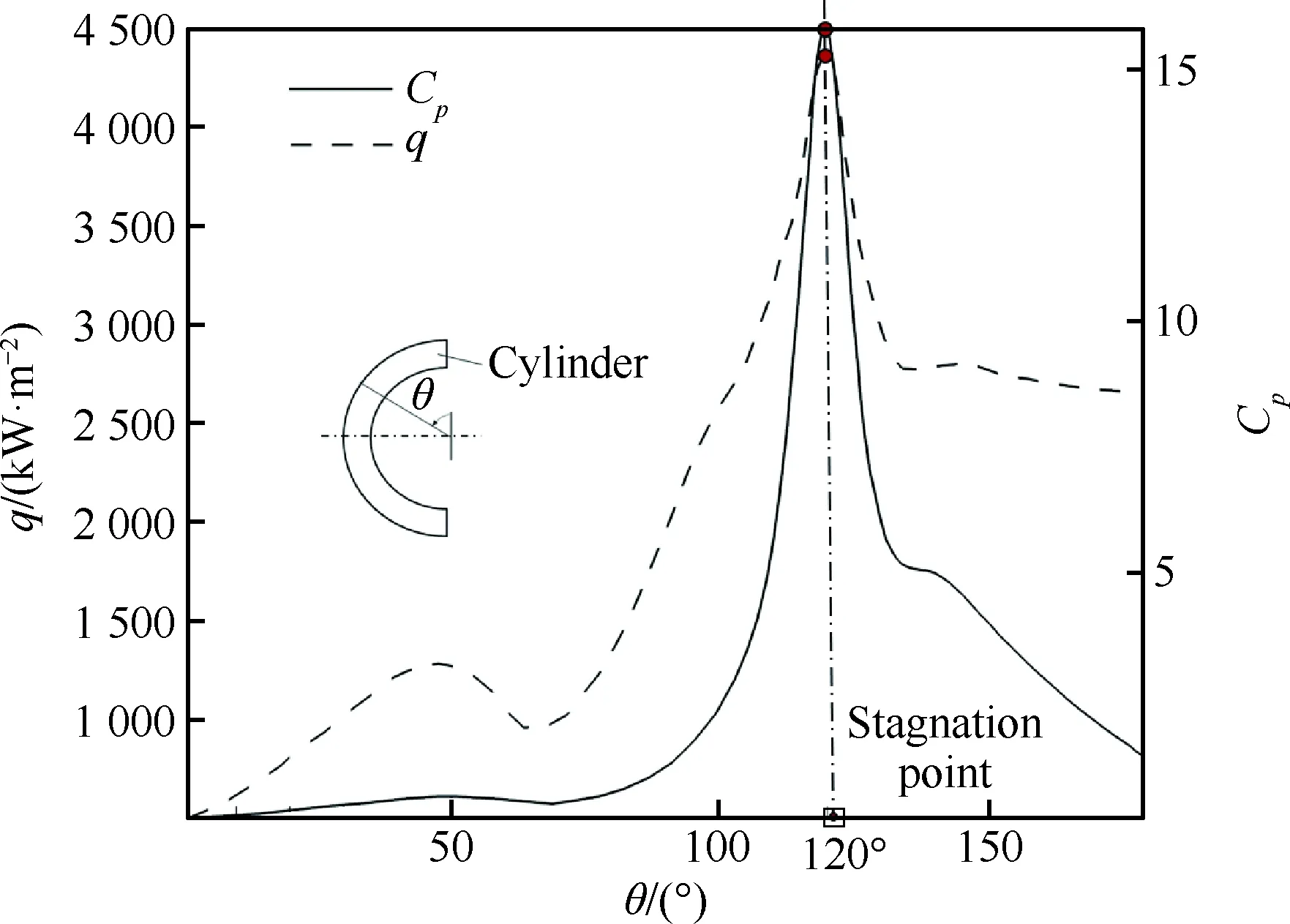
圖16 圓管表面穩態熱流與壓力系數分布曲線
Fig.16 Curves of steady surface heat flux and pressure coefficient distributions on cylinder

為了定量分析“Ⅳ型”激波干擾產生的高溫高壓效應，圖16給出了圓管表面穩態熱流與壓力系數(Cp)分布曲線。可以明顯看出，“Ⅳ型”激波干擾產生的超聲速“噴流”沖擊圓管壁面導致表面熱流與壓力系數出現顯著峰值。超聲速“噴流”沖擊壁面的作用位置大致位于120°的地方，在此處，表面熱流與壓力系數分別高達4 348.1 kW/m2和15.8。

值得一提的是，本定常算例也展示了本文一體化計算方法的優勢：可以高效求解復雜高超聲速流場下的流-熱-固耦合定常計算問題。傳統分區耦合計算方法在求解定常問題時，需要在時間域上進行大量的耦合交替迭代直至流場與固體結構溫度場定常收斂，因此必將導致計算效率的大幅度降低，相比之下，本文一體化方法可以很好解決這一問題。

3.2.2 非定常計算結果

圖17給出了非定常計算中不銹鋼圓管內部溫度分布隨時間變化的云圖(t=0.1,0.5,1.0,2.0 s)。從圖中可以直觀地觀察內部結構的溫度分布隨時間的演變歷程。由于“Ⅳ型”激波干擾的作用，產生的超聲速“噴流”不斷沖擊壁面，產生的高熱量首先在沖擊區域快速積累，導致該區域的圓管內部結構溫度急劇上升，形成一個顯著的高溫區。隨著時間的推移，“噴流”沖擊產生的高熱流持續傳入圓管結構內部且不斷延伸，導致結構內部整體溫度不斷升高，同時沖擊區域的高溫區域也不斷擴大。由此可見，“Ⅳ型”激波干擾的熱沖擊作用導致結構內部產生集中的高溫區，在此高溫區域必然會出現較大的熱應力集中現象，這也將是后續研究的重要內容。

圖18和圖19分別給出了圓管表面的壓力系數分布和熱流分布隨時間的變化歷程。同時，為了更好地對比分析“Ⅳ型”激波干擾產生的高溫高壓效應，圖中也給出了無斜激波干擾時，初始時刻圓管表面的壓力與熱流分布，并用此時的駐點壓力系數(Cp0)和熱流值對預測的“Ⅳ型”激波干擾壁面壓力系數和熱通量進行統一歸一化處理。

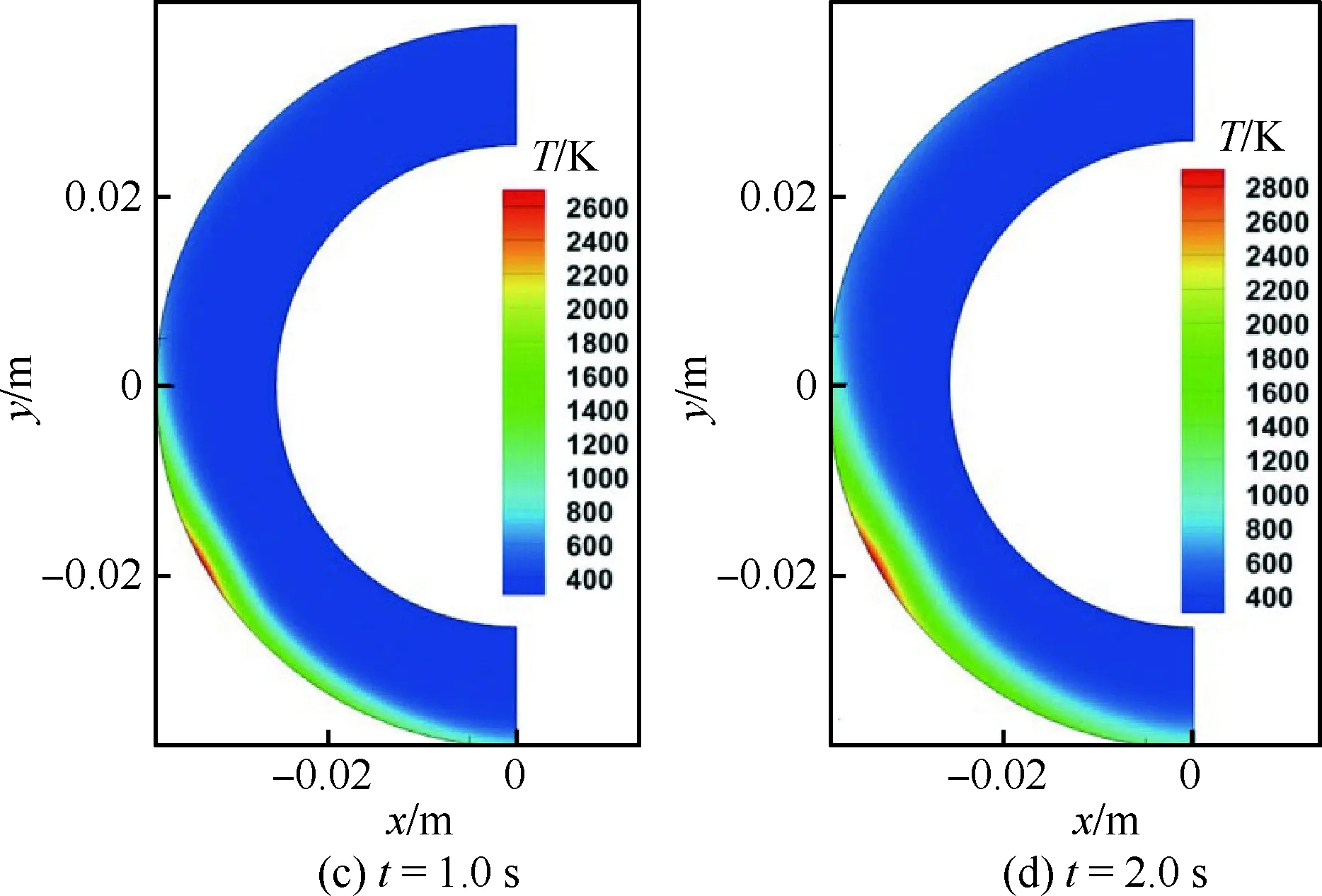
圖17 圓管內部溫度云圖隨時間變化歷程
Fig.17 Temporal variation of temperature contours within cylinder

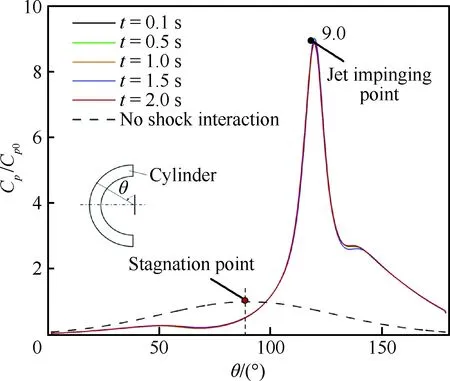
圖18 圓管表面壓力系數隨時間變化
Fig.18 Pressure coefficient variation with time along cylinder surface

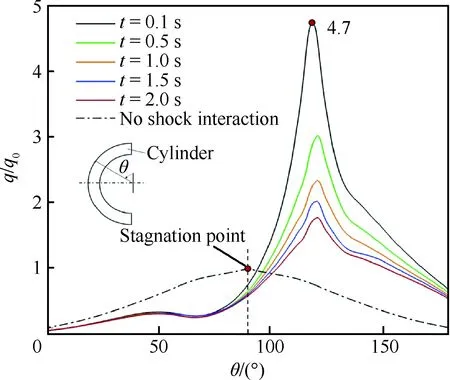
圖19 圓管表面熱流隨時間變化
Fig.19 Heat flux variation with time along cylinder surface

從圖18和圖19可明顯觀察到，“Ⅳ型”激波干擾的確導致圓管表面壓力和熱流急劇增大，且峰值都出現在超聲速“噴流”沖擊壁面區域。相比于無斜激波干擾的流動，“Ⅳ型”激波干擾的射流沖擊作用使得壁面最大壓力系數增大約9倍，壁面最大熱流增大約4.7倍，計算結果與文獻[32-33]吻合。由此可見，此類“Ⅳ型”激波干擾將極大放大外部高速流場對飛行器結構的氣動熱與氣動力載荷作用，給高速飛行器飛行安全造成極大安全隱患。另外，從圖中可以看出，隨著時間的推移，圓管表面壓力分布幾乎不隨時間變化，這說明圓管壁面壓力受圓管整體結構溫度變化的影響很小。然而，壁面熱通量的峰值隨著計算時間的推進逐漸減小。這是由于初始時刻壁面熱流峰值最大，圓管結構吸收氣動加熱熱量后，壁面溫度快速上升。壁溫的升高導致溫度邊界層內的溫度梯度減小，壁面熱流峰值減小，削弱了外部氣動加熱效應從而導致圓管結構溫升速率的降低。同時，結構溫升速率的降低反過來也會導致壁面熱通量的變化率逐漸減小。這些現象正是反映了流-熱-固相互作用的耦合特性。

綜上分析，高速飛行器在進行長航時飛行時，“Ⅳ型”激波干擾作用產生的高溫高壓沖擊載荷，極有可能造成飛行器熱防護結構的熱力學破壞從而形成嚴重的飛行安全隱患。因此，“Ⅳ型”激波干擾作用將給高速飛行器的熱防護設計與選材帶來嚴峻挑戰，需引起重要關注。

4 結 論

本文針對高超聲速進氣道前緣“Ⅳ型”激波干擾產生的氣動加熱與結構傳熱耦合計算問題，提出一種基于有限體積法的流-熱-固一體化計算方法，并采用經典高超聲速二維圓管繞流算例驗證了一體化方法的正確性與穩定性。采用所提出的一體化計算方法對高超聲速前緣“Ⅳ型”激波干擾中的流-熱-固耦合問題進行一體化定常/非定常計算分析，得到以下結論：

1) 采用經典高超聲速二維圓管繞流非定常算例對本文發展的一體化計算方法進行驗證分析，計算結果與參考文獻和風洞試驗結果吻合較好，證明了本文高超聲速流-熱-固一體化計算方法的可行性與可靠性，同時也證明了自適應時間步長控制方法的正確性。

2) 本文所提出的高超聲速流-熱-固一體化求解方法可以高效解決流場與結構傳熱穩態求解問題，較快計算出穩態結構與流場的溫度分布。計算方法進行全物理場統一迭代，可以很好地改善傳統分區耦合算法多次迭代計算效率低的不足。

3) 對高超聲速前緣“Ⅳ型”激波干擾流-熱-固耦合進行定常/非定常一體化計算分析，計算發現，“Ⅳ型”激波干擾作用產生的超聲速“噴流”不斷沖擊壁面，使得壁面最大壓力系數增大約9倍，壁面最大熱流增大約4.7倍，給高速飛行器的熱防護設計與選材帶來嚴峻挑戰。

為進一步探索高超聲速流-熱-固一體化求解方法的應用范圍，后續將研究“Ⅳ型”激波干擾作用產生的高溫高壓對結構熱力學變形產生的影響。