斜激波極值規律的邊界層影響

溫浩，史愛明，鄢榮

西北工業大學 航空學院 NPU-Duke空氣動力與氣動彈性聯合實驗室，西安 710072

超聲速飛行器氣動設計需要提高升阻比和降低音爆分貝值[1]。這兩個問題的核心研究對象則是超聲速飛行時必然會產生的激波。減弱甚至消除激波不僅可使超聲速飛行的阻力減小[2]，還可通過降低激波強度(本文以激波后壓強比激波前壓強表征)直接減小近場音爆分貝值[3-4]。

激波強度存在隨飛行馬赫數變化的規律。正激波的強度由波前來流馬赫數唯一確定[5]。對飛機設計來說，一維正激波強度規律是不夠的。史愛明和Dowell[6]研究了二維斜激波中的斜激波極值規律，表明相同流動偏角下，必然存在流線穿過斜激波時激波強度最小的來流馬赫數，且激波角與流動偏角在最優馬赫數下呈現為線性關系。Emanuel[7]研究了斜激波后掠的情況，當氣流偏角固定時，激波強度參數會隨后掠角變化出現極值點，并得出極值點位置馬赫數和后掠與否無關。Elaichi和Zebbiche[8]研究了總溫對圓錐流動的影響，從其研究結果的分析中可以得出：當圓錐錐角固定時，激波強度參數隨馬赫數變化也存在極值現象。因研究對象的不同，Emanuel和Elaichi都未能指出斜激波極值規律的存在。

為對斜激波極值規律在黏性流動中的適用性進行研究，嘗試將無黏流動中的斜激波規律拓展到黏性流動中。在黏性流動中，激波的最終狀態不僅取決于幾何外形，還會受到邊界層的影響。對于可壓縮流動中邊界層流動參數，一般會結合Blasius不可壓層流平板邊界層解[9]進行理論計算。可壓縮層流邊界層的理論分析發展產生了變換方法[10-12]和參考溫度法[13-15]，建立了可壓縮邊界層與不可壓縮邊界層參數間的關系。變換法對可壓縮邊界層方程進行簡化，往往應用于邊界層外流動參數與來流參數相差不大的情況[16]，對于復雜的工程應用來說精度較差。工程上則常用參考溫度法進行計算，高超聲速快速計算方法[17]、乘波體設計[18]均據此對邊界層影響進行分析計算。湍流流動較為復雜，往往通過近似的邊界層速度型分布得到邊界層參數[19]；可壓縮湍流邊界層的理論計算主要是參考溫度法[15]，變換方法則沒有邊界層厚度參數與Blasius解的關系研究。

本文建立了超聲速流動中的黏性楔面激波模型，分別使用Eckert參考溫度法[18](ERT)和Illingworth-Stewartson變換法[16](IST)進行了邊界層影響的計算，并與計算流體力學(CFD)[20]方法得到的結果進行比較。結果表明，單一的ERT方法結果較CFD偏低，而IST方法則恰好較CFD偏高，且二者的這種表現規律在湍流情況下更加明顯。因此建立基于ERT和IST的加權均值方法(WAM)。ERT的層流、湍流模型區別在于普朗特數導致的壁面溫度恢復系數的差別；因湍流模型較為復雜，IST的湍流模型設置為與層流一致，忽略湍流項導致的差異。邊界層理論模型的結果表明，黏性楔面激波同樣存在著極值規律。

1 楔面激波理論模型

1.1 可壓縮邊界層及楔面激波

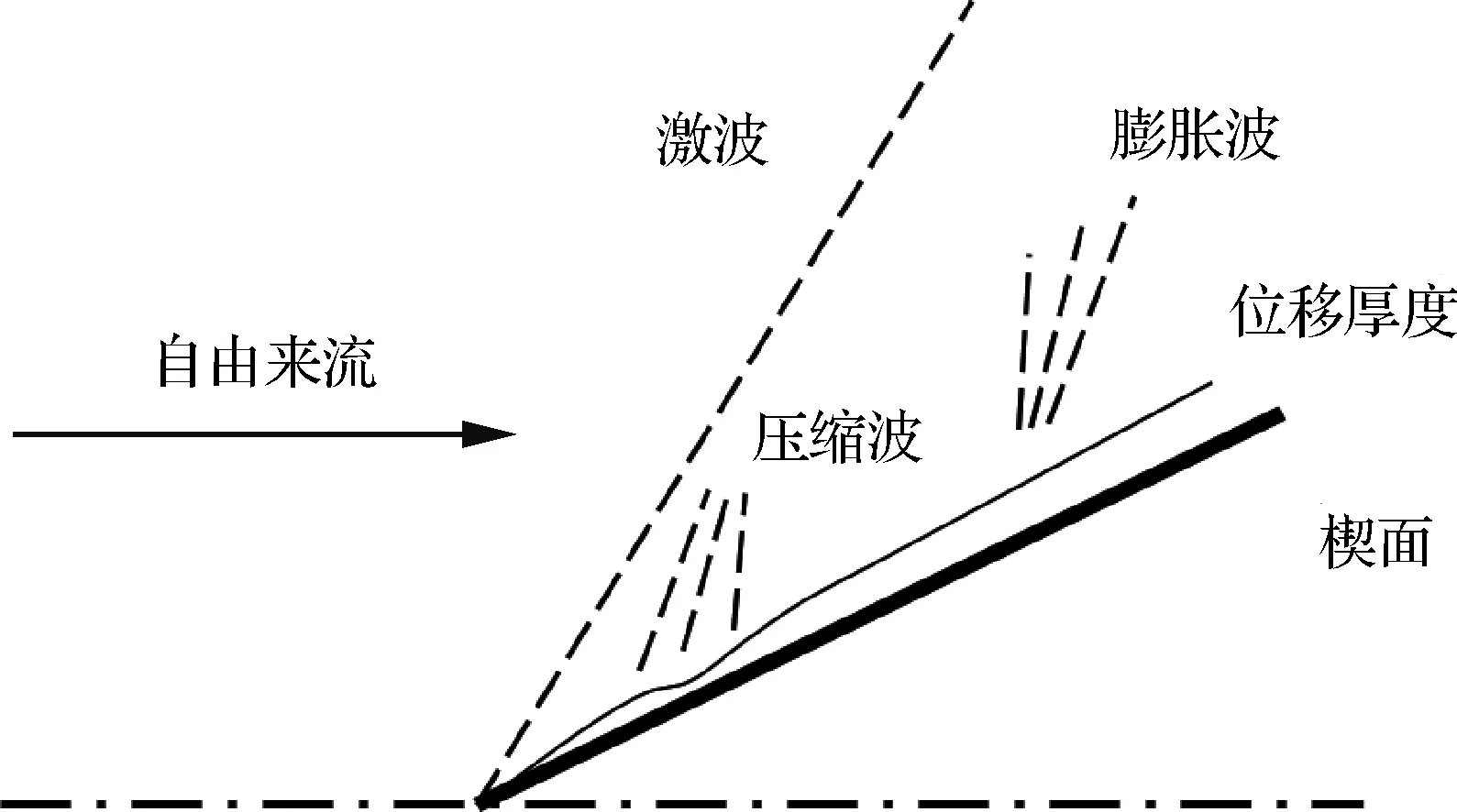
圖1 超聲速楔面黏性流動的激波結構Fig.1 Shock wave structure of supersonic wedge in viscous flow

楔面流動模型如圖1所示，在超聲速流動中存在一個二維楔面，楔面前不存在擾動。在特定的條件下，流體經過楔面會產生附體的斜激波；同時楔面附近因無滑移條件而產生邊界層，使得邊界層外的流線偏離楔面，偏離量可以用位移厚度表示。楔面模型邊界層的發展與平板類似，在層流邊界層和湍流邊界層處，邊界層位移厚度隨楔面長度增加，其增長率降低，流線偏離自身，產生膨脹波；在邊界層轉捩處，位移厚度先減小后增加，根據位移厚度增長率的變化產生壓縮波、膨脹波。因位移厚度變化率而產生的波與上游的激波相互作用，使激波略微彎曲：壓縮波使得激波強度增加，激波角增大；膨脹波則反之。

斜激波理論中，氣流方向的變化是激波產生的原因，經過激波的氣流偏角θ是斜激波結構的一個重要參數。無黏楔面流動中，經過激波的氣流偏角等于楔面與來流的夾角——楔面角θs，即無黏楔面激波結構具有θ=θs。黏性楔面流動中，邊界層會導致氣流偏角發生改變，全層流和全湍流時均具有θ>θs。1.2、1.3節將構建受邊界層影響的氣流偏角的計算方法，從而在1.4節中應用斜激波、膨脹波理論計算激波強度。

1.2 邊界層外流動參數

平板流動中，使用邊界層理論計算邊界層位移厚度等參數時，主要基于自由來流參數。而在楔面激波模型中，為使得計算更加準確，考慮以無黏理論確定的斜激波后參數進行計算。主要計算激波下游的單位雷諾數Reds和激波下游溫度T2。根據Sutherland公式計算黏性系數

(1)

式中:T為溫度；參考溫度Tv=273.2 K；常數c=110.4 K；黏性系數μ(Tv) = 1.72×10-5kg/(m·s)。

根據無黏理論，在已知來流馬赫數Ma1和無黏氣流偏角θs的條件下，可得激波后溫度與激波前溫度的比值T2/T1，從而得到激波后溫度T2。

(2)

式中：T1=300 K為設置的激波上游溫度；Man1為激波上游法向馬赫數；γ=1.4為比熱比；下標1表示激波前參數，下標2表示無黏理論確定的激波后參數，后文與此相同。根據式 (1)和式(2)，可以得到激波后黏性系數的比值μ2/μ1，進而由ρ1u1=ρ2u2(ρ、u為密度和速度)得到單位雷諾數之比及激波下游邊界層外的單位雷諾數Reds，表達式為

(3)

其中:Reus為斜激波上游的單位雷諾數。

1.3 可壓縮邊界層計算方法

1.3.1 層流邊界層計算方法

參考溫度法模型以參考雷諾數來代替不可壓縮Blasius解中的雷諾數，基于此進行邊界層的計算，其模型的發展更多關注于參考溫度的算法研究。ERT方法確定了參考溫度T*，其表達式為

T*=0.5(Tw+T2)+0.22(Tr-T2)

(4)

根據參考溫度法，得到參考雷諾數Re*=ρ*ued/μ*，其中：ρ*為參考密度；ue為邊界層外速度；d=1 m為特征長度；μ*為參考黏性系數。根據理想氣體狀態方程ρ*=p*/RT*(p*=p2表示激波下游壓強，R=287 J/(kg·K)表示氣體常數)，可以得到

(5)

式中：μ*由T*確定。取距離楔面頂點水平距離x位置為層流邊界層位移厚度的計算位置，則ERT方法確定的位移厚度為

(6)

求導可得x位置處流動方向相對楔面方向的偏轉角θΔ，其表達為

(7)

那么最終x位置處流線方向相對來流方向的偏轉角θef=θs+θΔ，如圖2(a)所示。

變換法也可建立與不可壓縮流動相似的可壓縮層流邊界層參數表示方法，該方法中Pr=1。對于ERT方法，Pr對最終理論模型結果的影響遠小于模型與CFD結果間的差距，可以忽略不計；這表明ERT方法和IST方法間的差距不在于Pr的不同，而在于自身模型的構建過程。IST方法確定的位移厚度為

(8)

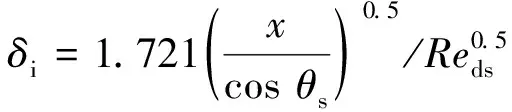
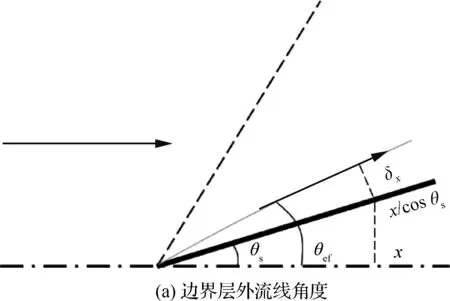
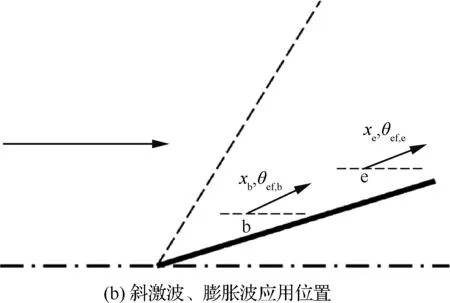
圖2 考慮邊界層影響的激波參數計算模型
Fig.2 Computation model of shock parameters with boundary layer effect considered

1.3.2 湍流邊界層計算方法

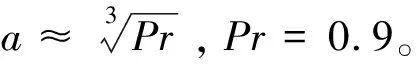
IST法中，式(8)相關的不可壓縮湍流邊界層厚度為

其余參數不變。之后計算可壓縮湍流邊界層造成的流線方向改變量為

1.4 可壓縮邊界層流場影響

對于全層流或全湍流流動，在來流馬赫數Ma1、楔面角θs、來流單位雷諾數Reus確定的情況下，隨著距楔面頂點水平位置x增大，δx逐漸增大，但θΔ卻逐漸減小。楔面流動中，楔面頂點附近壁面上會存在流動駐點，該位置處流動壓強等于總壓，之后隨流動發展，壓強會減小。在距離駐點足夠遠處，駐點總壓的影響可以忽略不計。邊界層理論可以確定不同x處的流線方向：x較小時，流動偏角增量較大；隨x增大，流動偏角增量降低。

對于邊界層影響量的計算，本文建立了斜激波和膨脹波的組合理論模型，用以計算x位置的無量綱壓強px/p1，也稱為激波強度。如圖2(b)所示，在位置b處，使用斜激波理論確定位置b的流動參數，以之模擬流動駐點的影響。依據可壓縮邊界層理論計算初始位置的氣流偏角θef,b；根據無黏斜激波理論，使用來流馬赫數Ma1和氣流偏角θef,b，確定初始斜激波強度px,b/p1等流場參數。假設b到e為等熵膨脹過程，根據b處流場信息，通過膨脹波理論和Prandtl-Meyer函數，計算e處對應的激波強度px,e/p1等參數。

膨脹波關系表示為

θef,b-θef,e=ν(Mae)-ν(Mab)

(9)

式中：Mab和Mae分別為b處和e處的馬赫數；ν分Prandtl-Meyer函數，有

(10)

其中：α=Ma2-1。根據等熵過程總參數不變即可求得

(11)

進而得到e處的激波強度px,e/p1。

至此，在楔面激波模型中，將斜激波和邊界層理論發展到了邊界層外流場參數的計算中。邊界層理論模型——ERT和IST方法會得出不同的激波強度計算結果。本節模型適用于邊界層為全層流或全湍流的情況。對于流動轉捩，需考慮轉捩過程中邊界層位移厚度的變化規律，同時在轉捩前后分別應用層流和湍流理論模型。

2 理論模型預測精度分析

2.1 數值方法與網格

使用CFD的方法進行評估時，分別進行無黏Euler方程、層流Navier-Stokes方程、湍流基于雷諾平均Navier-Stokes(RANS)方程的計算。本文Euler方程空間離散為二階守恒的單調迎風格式MUSCL[21]，與國內提出的無波動、無自由參數的耗散差分格式NND[22]相比，二者在數值計算的應用層面完全一致；限制器類型為Venkatakrishnan[23]，對流項處理的數值格式為Harten-Lax-van Leer-Contact (HLLC)[24]；時間離散為歐拉隱式(Euler-Implicit)；采用當地時間步、CFL數自適應、多重網格等方法加速收斂。層流Navier-Stokes方程無黏部分的離散格式與Euler方程一致，黏性項離散采用中心差分。湍流RANS方程湍流模型為Spalart-Allmaras(S-A)，湍流模型方程空間離散為一階標量迎風(Scalar Upwind)格式，時間離散為歐拉隱式[20]。

二維超聲速楔面黏性流動的計算網格如圖3所示，采用非等距四邊形網格。網格拓撲包括：與壁面平行的邊界層網格，與激波平行的邊界層外區域網格。沿壁面方向網格尺度最小為2×10-5m，線性增長，增長率為1.2，數據采集點處約為2×10-3m；垂直壁面方向網格尺度最小為4×10-7m，線性增長，增長率為1.2，數據采集點處約為7×10-4m。網格區域大小為0.4 m×1.2 m，總數為177×170；加密區域為激波和壁面附近，大小為0.03 m×0.02 m，數目為51×49。所有黏性CFD計算中，單位雷諾數Reus=3.5×107/m；所有CFD計算中，激波強度采集位置xe≈0.085 m。

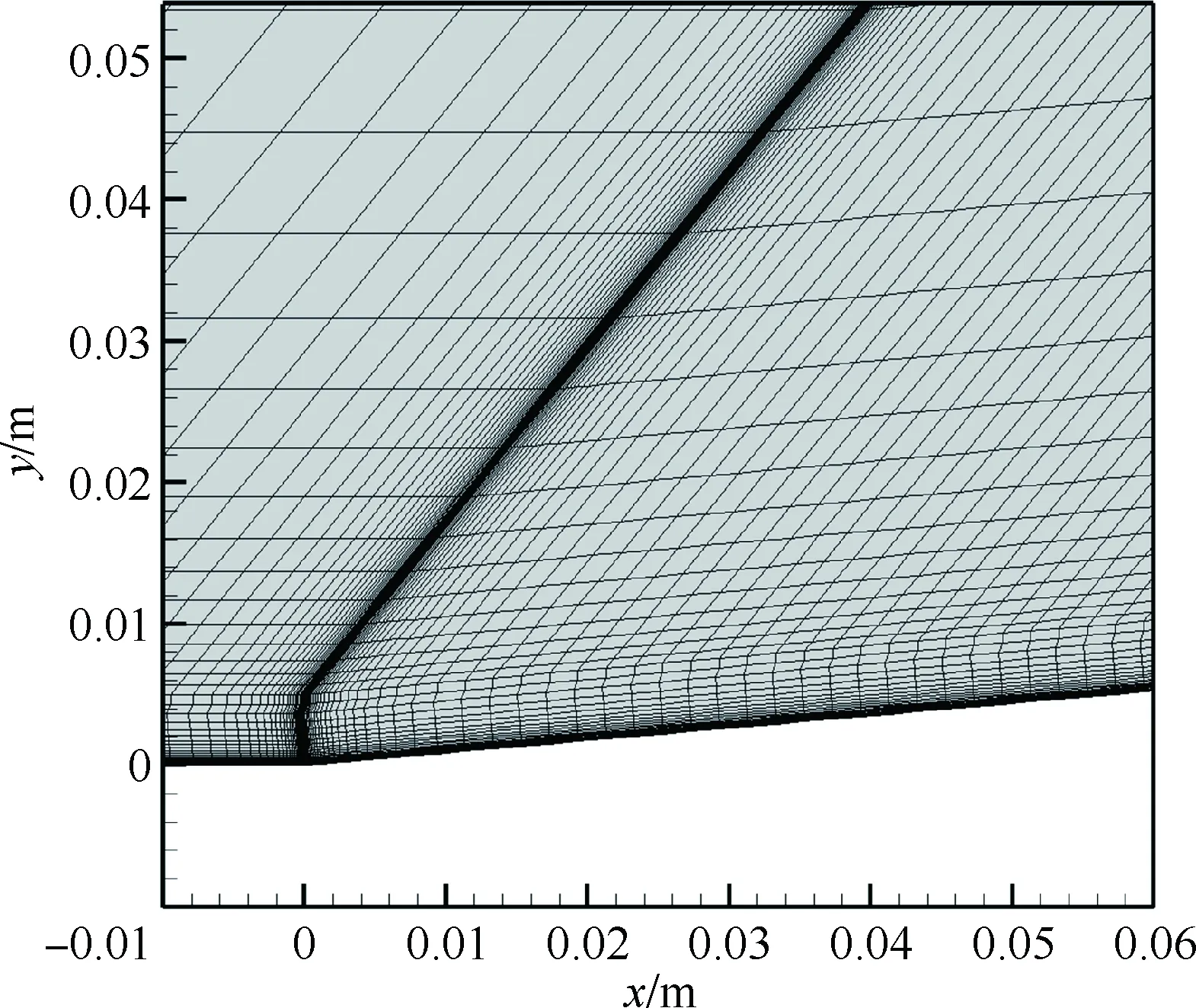
圖3 楔面激波數值模擬網格
Fig.3 Numerical mesh of wedge shock

2.2 理論模型中膨脹波部分的優化

本節及2.3節的CFD計算中，楔面角為3°，馬赫數計算點取Ma1=1.195 7、1.234 9、1.319 0、1.368 6、1.469 1、1.600 0、1.700 0、2.000 0、2.300 0，其中Ma1=1.469 1產生的無黏激波強度最小。

理論模型中，對流動駐點影響的考慮在于xb處定義的激波強度計算，模型中膨脹波理論描述了邊界層變化對激波強度的影響。模型中尚有xb未能確定，為分析其對xe處激波強度預測結果的影響，取Ma1=1.195 7、1.469 1、2.300 0結果進行研究。圖4為層流ERT結果的理論模型計算值分布，可以看到在xb>0.01 m(約xe/8位置)后，預測結果隨xb變化不大。在xb<0.01 m時，xb的影響較為明顯。特別是當xb接近0時，與其他xb相比，理論模型預測結果會產生較大變化。這是因為邊界層理論模型在xb為0時出現奇異值，使得預測的θΔ趨于90°。此時起始位置激波造成的壓強增大，之后膨脹波造成的壓強降低，二者在量值上都很大，造成最終計算精度的降低。xb>0.01 m后，xb影響的標準差為1.471 3×10-5，遠小于理論模型與CFD結果間差值的標準差1.581 8×10-4；IST結果、湍流結果也是如此。這表明在處理簡單的超聲速楔面流動時，單一的斜激波理論可以達到較好的精度。因此，后續理論模型對于激波強度的預測，可以直接在xe處應用斜激波理論，采集點處壓強寫為px。

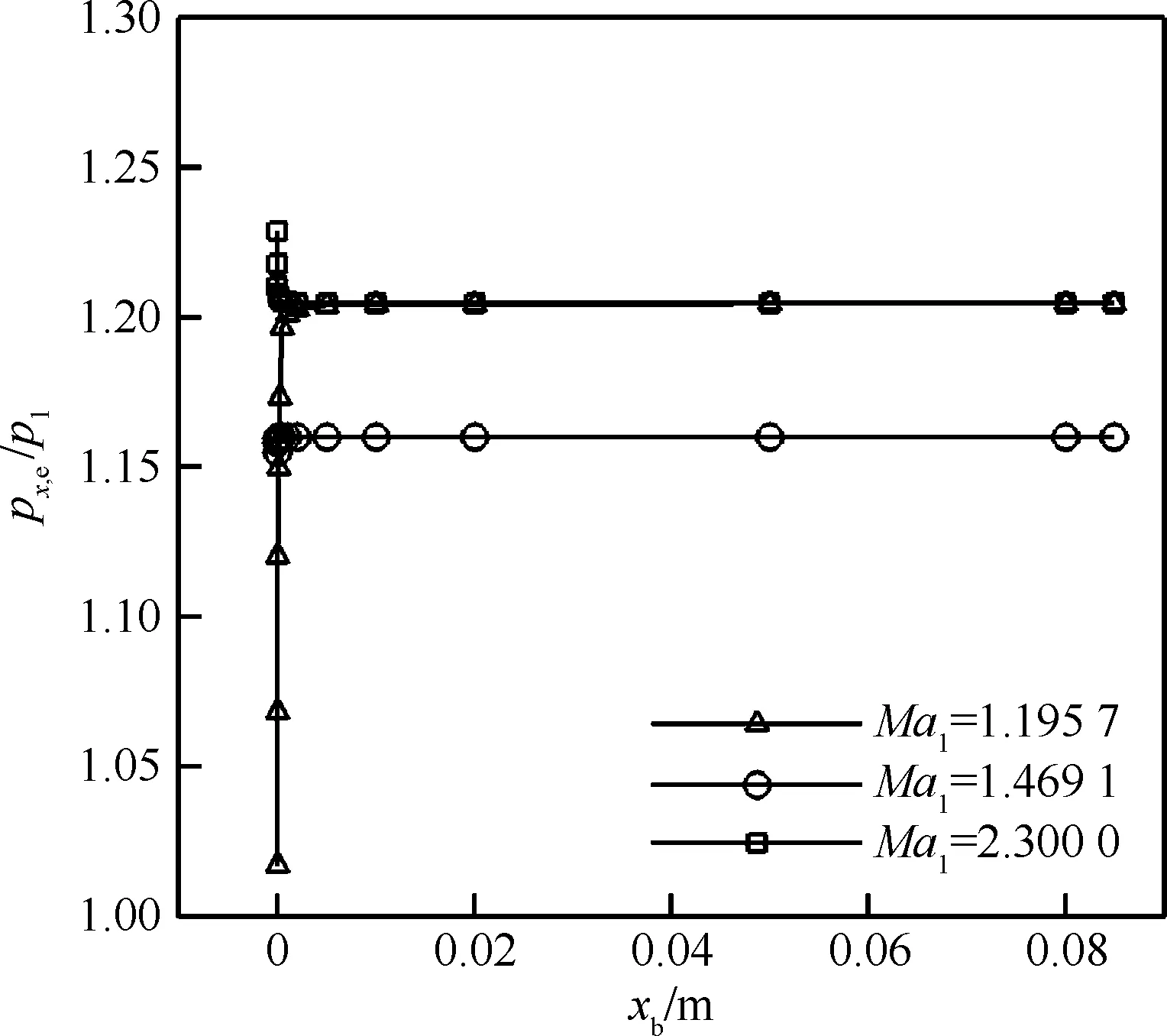
圖4 初始激波位置xb對層流ERT預測結果的影響
Fig.4 Influence of initial shock locationxbon prediction results of laminar ERT model

2.3 單一ERT和IST理論方法結果分析

下面根據層流和湍流的數值結果對理論模型的預測結果進行分析。圖5為理論模型預測結果與CFD間差距分析，圖中CFD表示層流或湍流計算結果，WAM方法將在2.4節具體敘述。可以看到，無論是層流還是湍流，在激波強度的預測上，ERT、IST兩種理論模型得到了隨馬赫數變化的極值現象，均與無黏理論表現一致。可以看到ERT的預測結果小于CFD結果，而IST的預測結果大于CFD結果，這在湍流結果中表現得更加明顯。這說明兩種邊界層方法具有各自的內在特點，且分別表現了對結果的低估和高估。因此考慮兩種模型的加權平均結果，以取得較好的黏性結果預測精度。

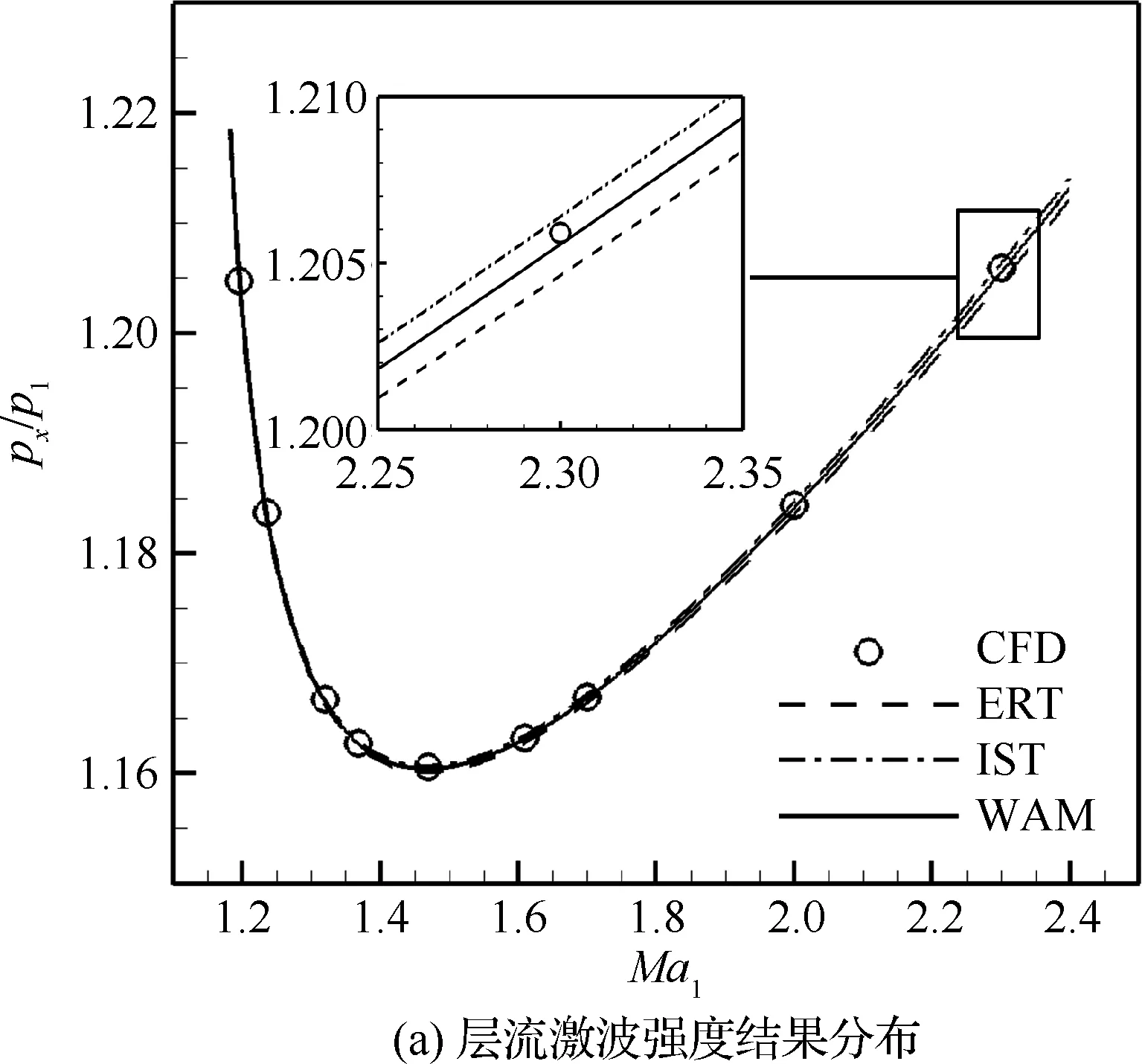
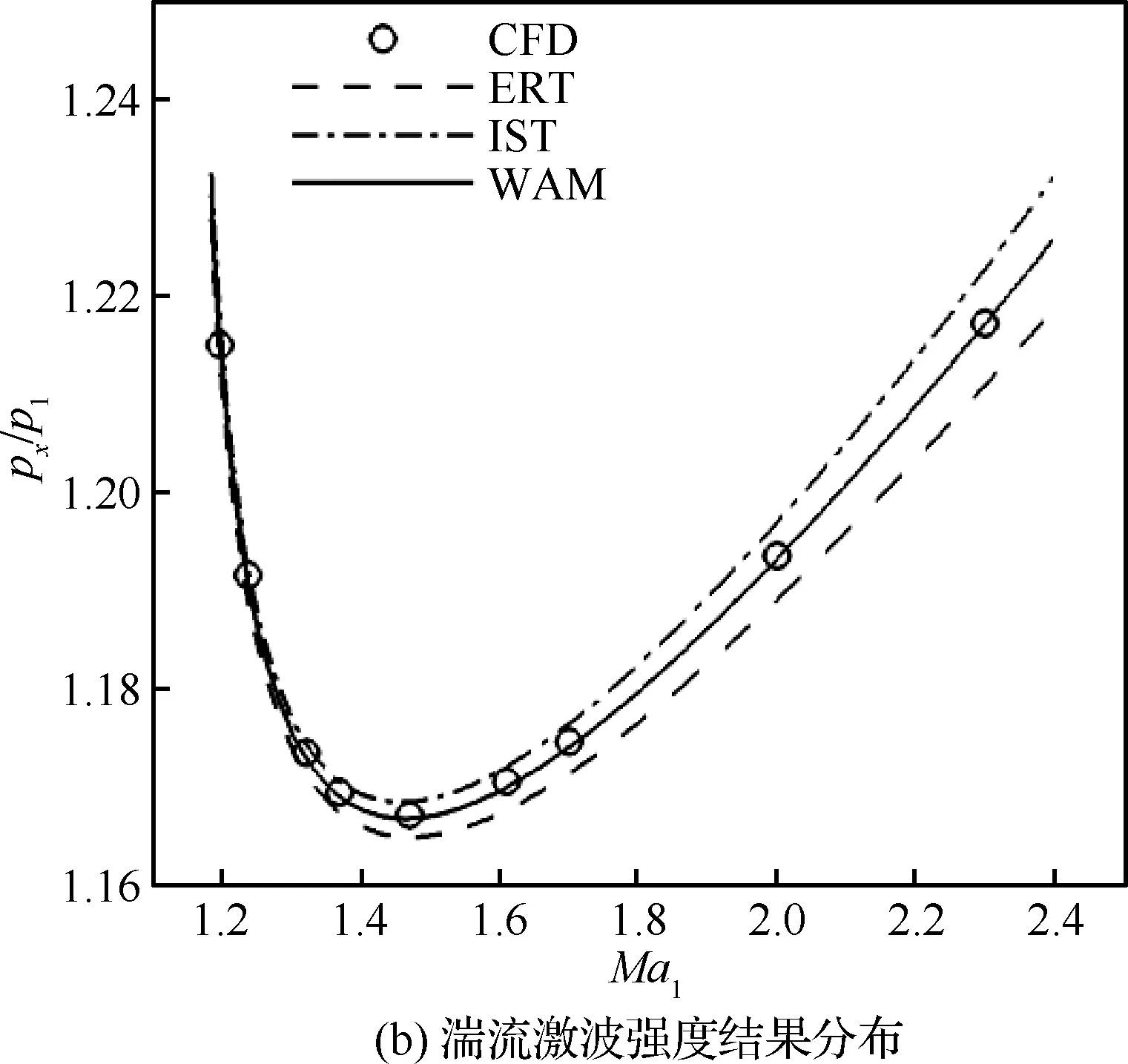
圖5θs=3°理論模型和CFD計算結果的對比
Fig.5 Comparison between theoretical model and CFD results atθs=3°

2.4 WAM方法及其結果分析

WAM方法的表達式為

(12)

式中:λ為加權因子。ERT和IST方法均采用無黏激波后參數作為邊界層參數來源。根據二者的理論方法構建過程，自變量參數可單一取為Ma2。

在λ的擬合上，考慮如表1所示的楔面角和來流馬赫數范圍來產生訓練集和測試集。θs=3°、5°、10°在相應的馬赫數范圍內每組取9個馬赫數點；而θs=20°、30°、35°時，每組取5個馬赫數點。各楔面角下馬赫數的設置基于激波強度極值規律，保證激波強度最小值點的存在。

Euler方程的計算結果表明，隨楔面角的增大，數值結果與無黏理論值間的差距增大，即大楔面角下，CFD結果不夠準確，如表2所示。層流和湍流的數值計算也是如此，故λ的擬合考慮角度θs=3°、5°、10°。因CFD結果與方程計算的精確值相比有一定的差距，但相較于理論與CFD間的誤差，這一差距并不大。因此，采用層流結果難以訓練出較為準確的λ值。而湍流結果中，這一誤差相比之下卻足夠小，得到的擬合前的λ分布也較為穩定。且湍流與層流使用的是相同的可壓縮處理方法，所以本文使用湍流計算結果來擬合λ，減少CFD本身誤差的影響。

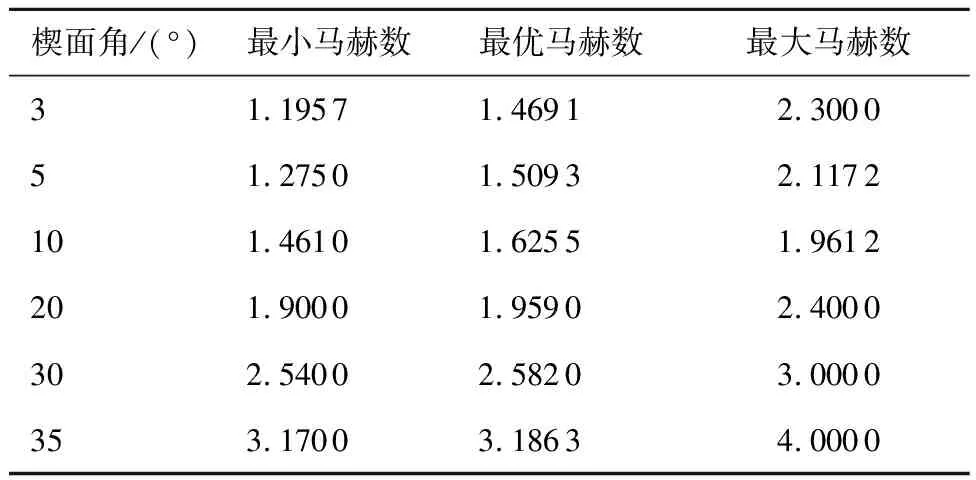
表1 CFD狀態點范圍Table 1 Condition range of CFD

λ經三次多項式擬合得到

(13)

下面對WAM模型的預測結果使用測試集進行分析，測試集選為全部計算黏性結果。WAM與CFD間的相對誤差為

(14)

式中：i=無黏理論，層流WAM，湍流WAM；j=無黏CFD，層流CFD，湍流CFD。對同一楔面角下的所有馬赫數結果相對誤差求標準差，得到相對誤差標準差分布如表2所示。隨楔面角增大，WAM與CFD間的相對誤差增大，在楔面角小于20°時，此時馬赫數范圍約為1.23.1，湍流WAM預測結果誤差與其他楔面角和層流結果匹配較差，這表明WAM模型在楔面角約大于30°的湍流結果的可信度開始迅速下降，預測相對誤差大于0.01；而層流結果則仍能保持一定精度。

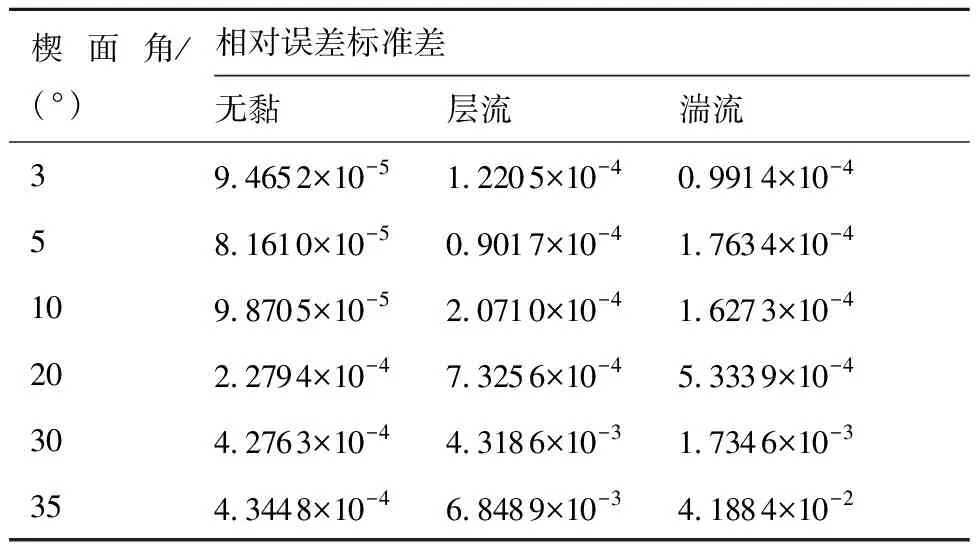
表2 WAM與CFD間的相對誤差標準差

在無黏斜激波規律中，隨著流動偏角θ的增大，最優馬赫數與激波恰好脫體時的馬赫數間的差距逐漸減小，這意味著斜激波極值規律在大流動偏角，或者說高馬赫數時，其適用性較差。因此對于所要研究的斜激波極值規律，WAM方法可以在合適的范圍內取得較好的預測精度。

3 邊界層對斜激波極值規律的影響

3.1 無黏斜激波極值規律討論

無黏流動中的斜激波極值規律表明，在相同的氣流偏轉角θ下，具有最小激波強度的波前馬赫數并不是激波恰好脫體的馬赫數值，反而大于該值；稱該最小激波強度下的來流馬赫數為最優馬赫數。該激波強度可以用壓強比、總壓損失率、溫度比衡量，在激波強度于最優馬赫數下取得極值時，壓強比等參數均會取得極值。該規律基于斜激波理論得到的法向馬赫數關系式為[10]

(15)

式中：θ為經過激波的氣流偏角，在無黏的超聲速楔面模型中，其等于楔面角θs；β為激波角，即激波面與來流方向的夾角。此關系式建立了斜激波空間結構參數θ、β與激波強度唯一變量Man1的關系。基于此，得到最優馬赫數為

(16)

同樣地，在確定馬赫數作為飛機設計約束、要求更小的飛行能量損失的情況下，穿過激波的流動偏角會趨向于0。因此在沒有其他約束作用的情形下，無法合理地設計出具有一定體積的超聲速外形，亞聲速飛行器設計也是如此，空氣動力學特性決定了更小飛行能量損失的飛行器永遠是厚度更小的類似設計。上述斜激波極值規律表明對于楔面激波，盡管在給定馬赫數下不存在最優的飛行器設計，然而一旦根據其他約束條件確定飛行器外形，那么便可以使用極值規律衡量飛行器外形和馬赫數需求的匹配度。

關于直接由飛行器外形變化產生的附體斜激波，主要有兩種形式。其一是本文研究的楔面激波類型，特點是斜激波的上游不存在邊界層[25]；其二為楔角流動類型，斜激波前存在邊界層，因此產生的斜激波與邊界層相互作用，使得激波振蕩，流場與無黏理論解間差距較大[26-28]。這為斜激波極值規律的應用提供了新的思路，比如對于楔角流動所產生的斜激波，其最優馬赫數如何變化、其振蕩幅值和頻率是否表現對稱性，這都是可以深入研究的方向。此外，經典的入/反射激波與平板邊界層相互作用，分離泡、流動轉捩的相關特征會如何變化，這是斜激波極值規律應用的另一個探索[29-30]。

3.2 最優馬赫數及激波強度變化

數值驗證的結果表明，在最優馬赫數附近，楔面角不大時，WAM方法取了得良好的精度。

首先考慮最優馬赫數的變化。在加入了黏性邊界層的影響后，楔面角θs≈3°～20°范圍內，關于最優馬赫數的變化，層流增量為0.001 5～0.003 3，湍流增量比層流稍大，為0.002 8～0.006 1，且二者均隨楔面角增大而增大。圖6為加入邊界層影響后，最優馬赫數Ma1隨θs變化的情況。這表明邊界層不會使得該Ma1產生較大變化；由局部放大圖可知湍流Ma1增量約為層流2倍，20°時的增量約為3°時的2倍。

根據楔面邊界層變化規律，在距楔面頂點水平位置大于參考位置0.085 m處，最優馬赫數的增量會更小，反之則更大，這里取θs=10°進行討論。在百倍于參考位置，即約10 m處，黏性最優馬赫數的增量相比參考位置減小，層流不大于0.000 2，湍流不大于0.000 6。在距楔面頂點約0.01 m，接近理論模型奇異點處，最優馬赫數增量比參考位置增加，層流和湍流均不大于0.000 6。這表明在約0.01～10 m的較大范圍內，于參考位置0.085 m處得出的最優馬赫數的變化規律可對整個區域的結果進行表征。所以之后的討論仍是基于參考位置的數據。

圖6 邊界層對最小激波強度馬赫數的影響
Fig.6 Changes of Mach number of minimum shock strength influenced by boundary layer

其次考慮激波強度受到的影響。激波強度增量Δ(px/p1)與最優馬赫數增量類似，其相比無黏激波強度值變化很小。圖7為層流狀態下，激波強度增量Δ(px/p1)的分布。圖中：LMS表示無黏最小激波強度線，有黏下的最小激波強度線基本與無黏結果一致；βs指無黏超聲速楔面模型中，由Ma1和θs經無黏斜激波理論確定的激波角。圖中激波強度增量分布存在極小值點，極值點馬赫數大于最優馬赫數。

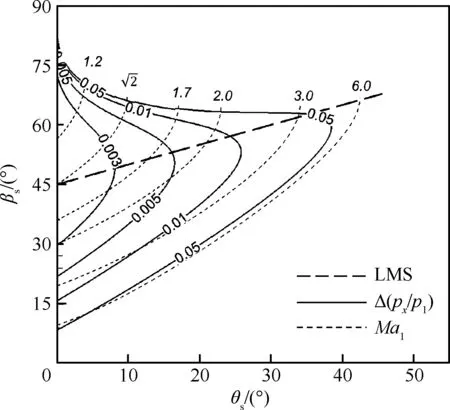
圖7 激波強度增量分布
Fig.7 Distribution of increments of shock strength

3.3 激波強度變化的理論解釋

為理解從無黏斜激波關系到加入邊界層影響后的激波強度和最優馬赫數的變化，將受邊界影響的激波強度px/p1表示為無黏激波強度項與激波強度增量項之和：

(17)

式中：p2/p1為無黏激波強度。根據斜激波理論，激波強度自變量取為來流馬赫數和楔面角，即p2/p1=f(Ma1,θs)。并且最終，邊界層導致的流線偏角變化仍是代入無黏斜激波理論，從而計算激波強度變化。根據無黏斜激波理論，Δ(px/p1)的一階展開為

(18)

其中：

(19)

圖8為無黏激波強度梯度項?(p2/p1)/?θs和層流流動偏角增量θΔ的空間分布。無黏激波強度梯度項的極值點馬赫數異于最優馬赫數。層流流動偏角增量項不存在極值點，其隨馬赫數單調增加。

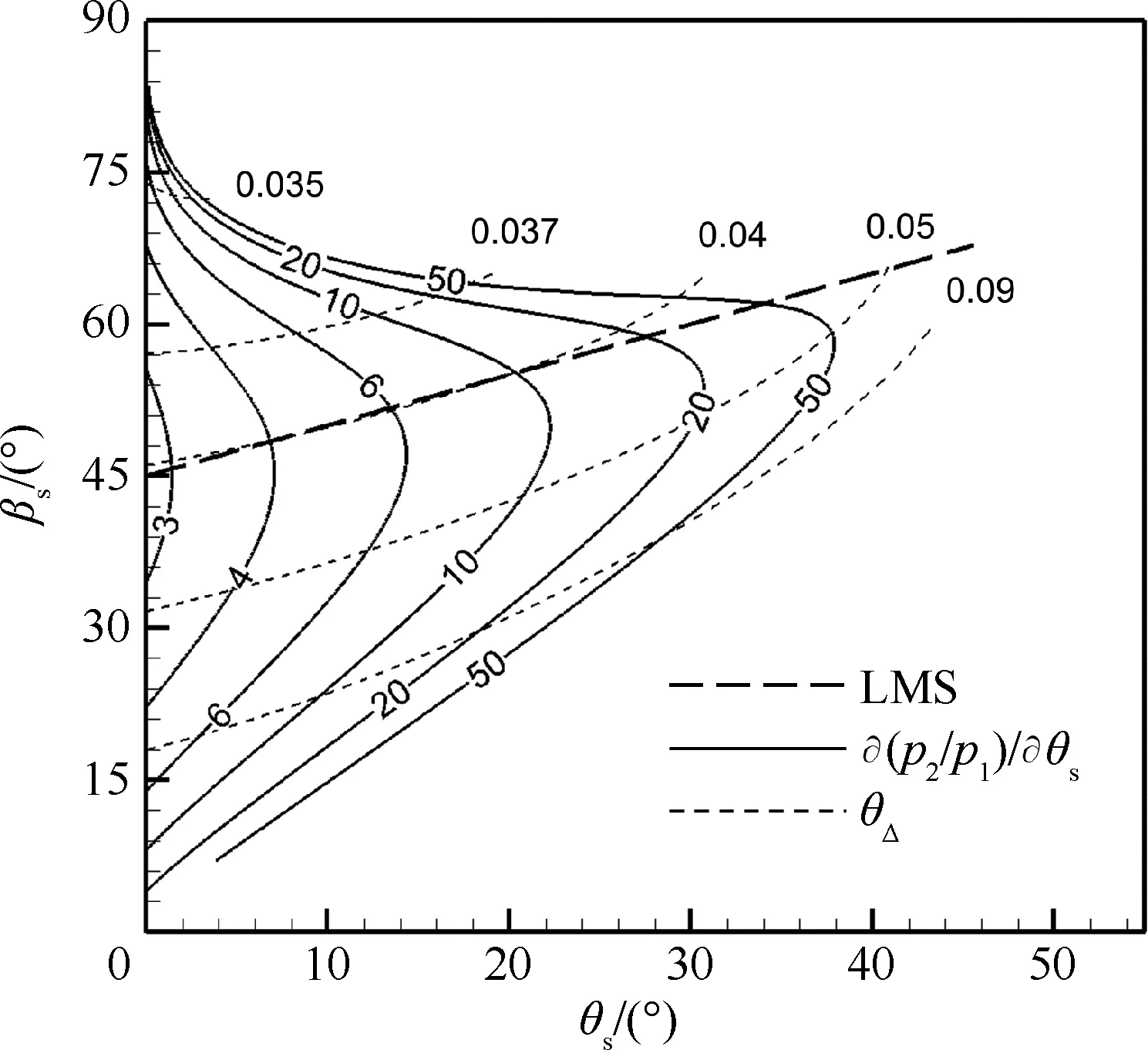
圖8 激波強度增量項的分解結果
Fig.8 Terms decomposed from increments of shock strength

圖9為LMS線上湍流和層流情況下的激波強度增量比值及流動偏角增量比值。LMS線上，湍流自約θs=37.9°開始激波全部脫體，而層流自約θs=40.4°開始脫體。圖9中，在較大的楔面角范圍內，激波強度增量比值和流動偏角增量比值保持了較好的一致性：楔面角小于20°時，二者相對差距不超過0.5%；在楔面角小于25°時，二者相對差距不超過1%，在楔面角小于30°時，二者相對差距不超過2.5%。因此，在WAM-CFD誤差較小的楔面角范圍內(3°～20°)，Δ(px/p1)使用式(18)預測，其誤差相比精確的斜激波理論不大。在楔面角大于35°后，二者差距已超過7%，此時不宜使用式(18)進行Δ(px/p1)的預測。

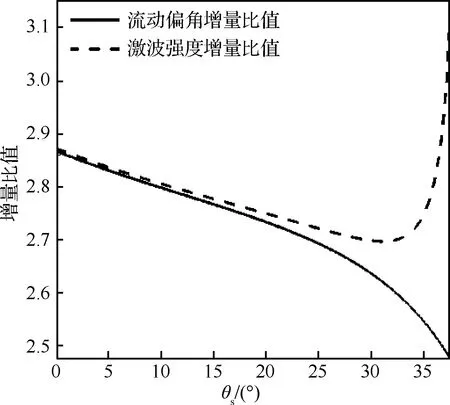
圖9 LMS線上湍流和層流偏角增量、激波強度 增量比值
Fig.9 Ratio of increments at turbulent and laminar case for deflection angle and shock strength at line LMS

至此確定了在LMS線附近的區域內，邊界層導致的激波強度增量和其導致的流動偏角增量呈較為準確的線性關系，系數為無黏激波強度梯度項。相對于激波強度的極值點馬赫數，激波強度增量與激波強度梯度的極值點馬赫數均較大，這一分布關系使得最優馬赫數增大。

4 結 論

1) 建立了黏性楔面激波強度計算的理論模型，初步定量地確定了邊界層厚度對楔面激波強度影響規律，為超聲速黏性楔面流動問題研究提供了精度尚可的斜激波參數理論計算方法。通過研究計入邊界層等效厚度影響的斜激波強度極值規律隨馬赫數、楔面角的變參規律，將斜激波強度極值規律拓展到了黏性楔面流動范疇。

2) 理論模型顯示：① 邊界層位移厚度使斜激波極值規律最優馬赫數略微增大，增加量在千分位；② 當楔面角小于20°、馬赫數小于2.3時，理論模型結果與CFD結果的相對誤差不大于0.1%；③ 層流與湍流邊界層對斜激波極值規律的影響程度不同；湍流邊界層導致的氣流偏角增量約是層流邊界層的2倍，最優馬赫數增量也約是層流邊界層的2倍。

3) ERT和IST的加權模型僅適用于全層流或全湍流流動，且對于高馬赫數(Ma>2.5)和大楔面角(θ>30°)情況，預測結果開始變得不理想(相對誤差大于0.2%)。計入轉捩因素的楔面斜激波理論模型是進一步的研究方向。文章討論了楔面上游為自由來流的楔面斜激波，楔面上游為壁面的楔面斜激波則是接下來的研究內容。這兩種激波是超聲速飛機內、外流問題生成斜激波的主要形式。

致 謝

感謝審稿人對論文研究工作的點評和實質性提高論文撰寫質量的指導。感謝聯合實驗室合作者美國杜克大學Earl H. DOWELL院士對本文研究內容的探討及英文摘要的修改。