基于偏最小二乘法的集裝箱吞吐量預測模型研究

丁文濤，劉孟琦，齊 越，蘇孟超，李宜軍，房 卓

（1.交通運輸部規劃研究院，北京 100028；2.大連理工大學建設工程學部，遼寧 大連116023）

引言

集裝箱運輸是現代交通的重要發展方向，也是港口地位和功能的重要標志，科學準確地預測港口集裝箱吞吐量，對于指導港口發展和建設具有重要的意義。目前港口集裝箱吞吐量預測方法可以分為兩大類，即定性預測方法和定量預測方法，常用的定性方法有Delphi法、專家調查法等，定量預測法有因果分析法、時間序列分析法、組合預測法等。如戴霖，黃浩[1]等建立馬爾科夫模型預測港口吞吐量，劉明維[2]等利用指數平滑法進行吞吐量預測，劉長儉[3]等采用 BP人工神經網絡構建港口集裝箱吞吐量預測模型，朱小檬[4]等基于時間序列-因果分析法相結合的方法對海港集裝箱吞吐量進行中長期預測，陳昌源[5]等利用改進的 GM(1,1)對上海港集裝箱吞吐量進行預測。

綜合來看，傳統方法多基于少量解釋變量，造成數據信息的流失，并且無法很好地解決解釋變量間的共線性問題。另一方面，這些方法都需要足夠多的歷史數據來支撐，更適用于集裝箱運輸發展較為成熟的港口。我國有較多港口的集裝箱運輸尚處于起步發展階段，傳統的方法較難預測未來的吞吐量規模。偏最小二乘法（PLS）能夠較好解決解釋變量共線性及樣本數量過少導致的無法有效建模的問題，因此本文采集影響港口集裝箱吞吐量的眾多影響因素并利用PLS方法建立預測模型。

1 偏最小二乘回歸建模

1.1 建模思想

偏最小二乘法（PLS）是由瑞典統計學家Herman OA Wold和Svante Wold一起開發的線性回歸模型，最初應用于社會科學領域，現在主要應用在化學計量學領域并廣泛應用于其他領域。PLS方法將主成分分析與多元線性回歸和典型相關分析結合到一起，將自變量和因變量投影到新空間提取主要成分，按照相關性程度排序確定提取成分個數后，建立線性回歸模型。相比標準回歸，PLS方法特別適用于自變量存在多重共線性和預測變量矩陣維度多于觀測值的情況。

1.2 基本原理

設自變量為矩陣En×m，因變量為矩陣Fn×p。將矩陣進行數據標準化，每個樣本減去一個維度變量均值然后除以該維度的標準差。自變量矩陣標準化后為E0(n×m)，因變量矩陣標準化后為F0(n×p)。

提取主成分t1：

提取主成分u1：

式中：w1為權重系數且為單位向量，；c1為權重系數且為單位向量，。

根據主成分原理和典型相關分析，t1與u1的方差達到最大且t1與u1的相關度達到最大值。故要求：

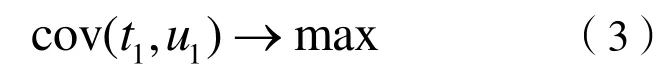
通過拉格朗日方法求解，w1為矩陣E0′F0F0′E0的最大特征值的特征向量，c1為矩陣F0′E0E0′F0的最大特征值的特征向量，并且均單位化。解出w1，c1即可求出t1與u1。

從而建立E0，F0對t1與u1的回歸方程：式

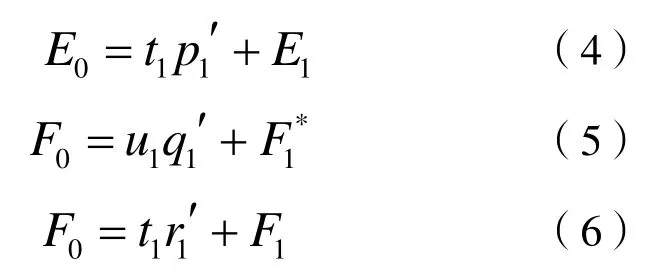
中：E1,F1*,F1是三個回歸方程的殘差矩陣。

用E1和F1取代E0和F0，按照上述過程，求出第二個軸w2和c2以及t2和u2，并重新建立E1和F1與t2和u2的回歸方程，直到求出所有主成分。（何時終止提取成分，后文詳述）

若E0的秩為A，則可以得到：

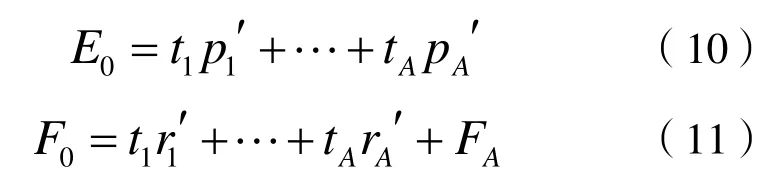
由于t1,…tA都是E01…E0m的線性組合,m=1,2,…，帶入上式中，可得到：

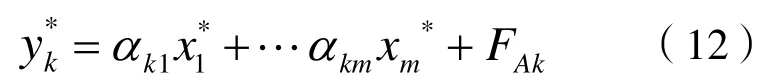
式中：k=1,2,…，且FAk為殘差矩陣FA的第k列。

確定提取主成分的個數th：

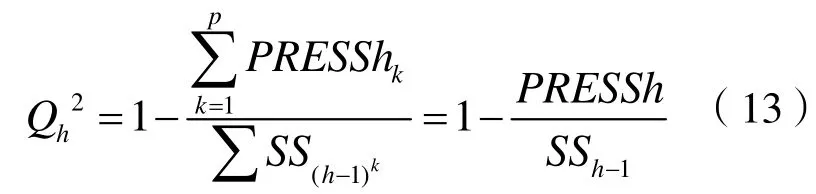
當Qh2≥(1-0.952)=0.0975時，th成分邊際貢獻顯著，可以確定h，然后將其轉化為y與x1,x2,…xh的回歸方程[6]。

1.3 變量投影重要性分析

每一個自變量在解釋因變量作用的重要性程度可以用變量投影重要性（VIP）來分析，具體的計算公式為：

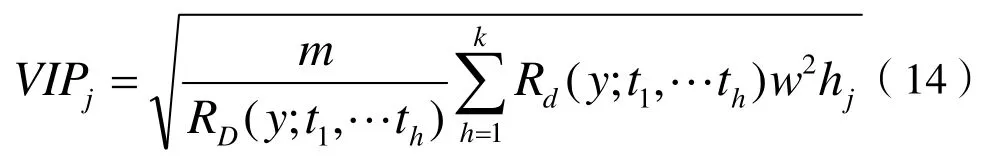
式中：VIPj是第j個變量xj的投影重要性指標；m為自變量個數；whj是wh的第j個分量；RD(y,th)是th對y解釋的變異精度；是t1…th對y的累計解釋能力。

2 算例分析

為了驗證偏最小二乘回歸模型的有效性和準確性，本文擬采用黃驊港進行驗證。黃驊港于2012年開始運營集裝箱業務，實現了年均40 %以上的快速增長，2018年完成集裝箱吞吐量72萬TEU。新

時期，“一帶一路”、京津冀協同發展、設立雄安新區等重大戰略陸續實施，黃驊港的發展環境發生了較大的變化，科學把握未來集裝箱吞吐量是十分必要和有意義的。

2.1 數據選取

集裝箱吞吐量與港口腹地的經濟發展和基礎設施的規模密切相關，根據對黃驊港集裝箱裝箱貨物及貨源地的調查，選取影響黃驊港集裝箱吞吐量的相關因素如下：滄州市生產總值（x1，億元），滄州市全社會固定資產投資值（x2，億元），滄州市消費品零售值（x3，億元），滄州市外貿進出口值（x4，億美元），滄州市出口值（x5，億美元），滄州市公路里程（x6，萬km），滄州市海鐵聯運量（x7，t），河北省生產總值（x8，億元），河北省糧食產量（x9，萬t），河北省第二產業總值（x10，億元），河北省第三產業總值（x11，億元），河北省進出口總值（x12，億美元），河北省鐵路運營里程（x13，km）以及黃驊港集裝箱吞吐量（y，TEU），具體數據見表1。

表1 黃驊港集裝箱吞吐量影響數據采集

2.2 多重共線性診斷

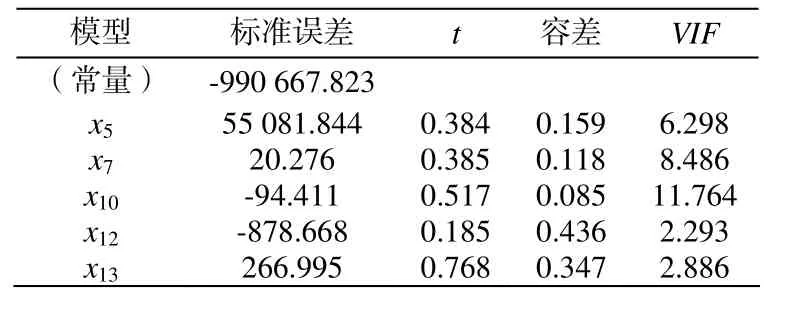
表2 回歸系數

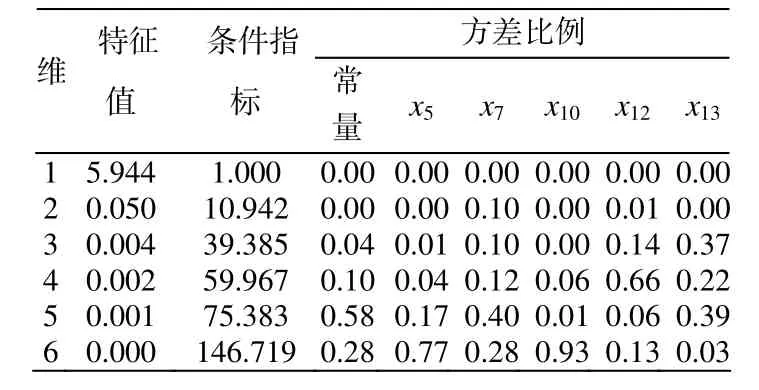
表3 多重共線性診斷

黃驊港 2012年才開始發展集裝箱業務，樣本數量小于變量數量，且經過SPSS初步計算，相關系數大于0.96，有嚴重多重共線性問題，采用普通的回歸方法無法建立回歸方程，一般的方法是采用逐步回歸方法建立多元回歸方程。

經過SPSS軟件計算，得出的多元回歸方程的回歸系數以及多重共線性診斷如表2和表3所示。

從表2中可看出，經過逐步回歸后的變量VIF值依舊偏大，其中x10的VIF值大于10，從表3中可以看出最小特征值為 0，其中最大方差比例達到0.93，接近于 1，可以看出逐步回歸后建立的多元回歸方程多重共線性依舊很嚴重，本文采用PLS方法解決共線性問題建立預測模式。

2.3 集裝箱吞吐量偏最小二乘法回歸方程確定

利用 SPSS軟件中的 PLS算法，選取2012—2016年影響黃驊港集裝箱吞吐量的13個因素進行偏最小二乘法，將 2017年數據用于檢驗方程，最終經過計算選出4個主成分（h=4），計算結果如表4所示。

可以看出，前4個主成分可完全解釋自變量和因變量的信息，即選取4個主成分可準確地提取信息。

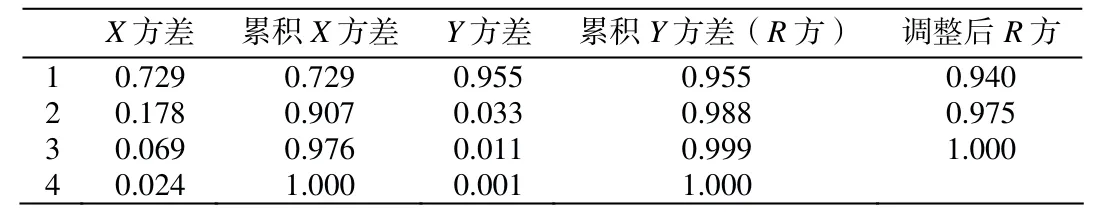
表4 已解釋的方差比例

通過軟件計算結果可以得到標準化偏最小二乘回歸方程：

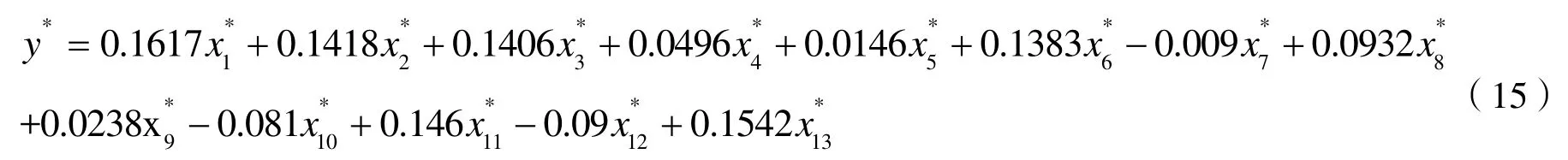
將標準化偏最小二乘回歸方程中的標準化因變量還原成普通變量，得到黃驊港集裝箱吞吐量與各自變量的回歸方程：

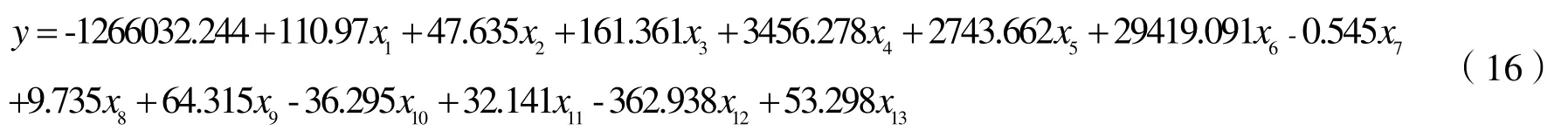
2.4 擬合效果和預測效果分析

將 2012—2016年各自變量數據帶入預測模型中得到擬合值（見表5），與實際值相比較并算出兩者的殘差值（見表5和圖1）。將 2017年各自變量數據帶入預測模型中得到 2017年吞吐量預測值并與實際值比較檢驗模型預測精度（見表6）。

表5 黃驊港集裝箱吞吐量實際值與預測值比較

表6 黃驊港集裝箱吞吐量2017年預測結果

圖1 黃驊港2012—2016年集裝箱吞吐量實際值與預測值比較

從圖1中看出，黃驊港集裝箱吞吐量實際值與擬合值擬合效果良好，從表5中看出擬合值與實際值殘差值都在1 %以內，可以見得偏最小二乘法能夠有效的消除多重共線性，得到精確度較高的回歸模型。從表6中可以看出，采用偏最小二乘回歸模型預測誤差在5 %以內，預測精度較高。

2.5 變量投影重要性指標（VIP）

計算出影響黃驊港集裝箱吞吐量變量重要性指標并繪制直方圖（見圖2），從圖中可以看出，滄州市生產總值、滄州市社會固定資產投資值、滄州市消費品零售值、滄州市公路里程數、滄州市海鐵聯運量、河北省生產總值、河北省農業產量、河北省第三產業總值、河北省鐵路運營里程這9個因素的投影重要性指標大于1，說明這9個指標是影響黃驊港集裝箱吞吐量的重要因素。

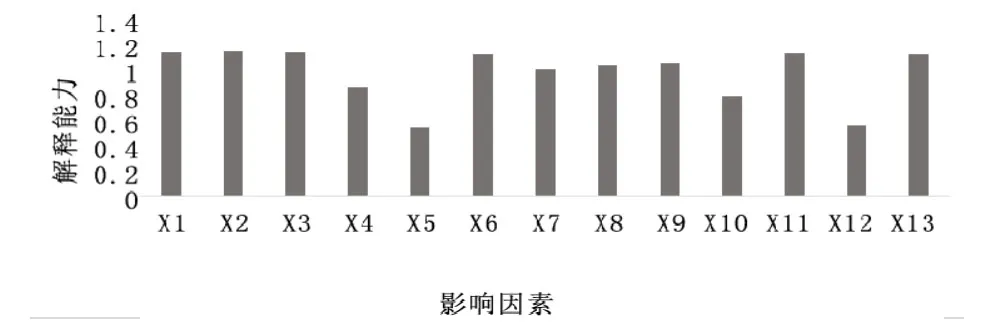
圖2 變量投影重要性指標

2.6 回歸結果解釋

從得到的回歸方程中可以看出滄州市生產總值、滄州市社會固定資產投資值、滄州市消費品零售值、滄州市外貿進出口值、滄州市出口值、滄州市公路里程、河北省生產總值、河北省農業產量、河北省第三產業總值、河北省鐵路運營里程對集裝箱吞吐量起促進作用，而河北第二產業總值和河北進出口值對黃驊港集裝箱吞吐量起負向作用。

黃驊港正在大力發展煤炭、糧食運輸的“散改集”，這占現有集裝箱吞吐量的70 %，而目前工業適箱貨運量還沒有得到充分釋放，腹地工業產生的集裝箱多由天津港運輸，所以河北省第二產業總值對黃驊集裝箱吞吐量影響有限。隨著滄州渤海新區的發展，臨港工業所產生的適箱貨運量將會逐步增加，這在以后的建模中要加入進去。黃驊港腹地冀中南地區外貿集裝箱主要經天津港出口，所以河北省外貿進出口額對黃驊港集裝箱吞吐量影響很小。隨著津冀港口公司參與到黃驊集裝箱碼頭運營，以及中韓自貿協定的推動，黃驊港承擔內支線運輸將逐步增加，近洋直航也將在未來開辟，這也要在以后的建模中考慮。

2.7 黃驊港集裝箱吞吐量中長期預測

將影響吞吐量因素的指標按照灰色模型法GM(1,1)進行預測，并且將預測的影響因素值帶入建好的偏最小回歸二乘模型，預測2020年和2025年的黃驊港集裝箱吞吐量，結果見表7。

表7 2020年和2025年黃驊港集裝箱吞吐量預測結果

3 結語

通過 PLS方法能夠提取變量中解釋性強的成分，去除變量中多重相關信息，保留變量原有信息，該法能夠最大限度的利用影響港口集裝箱吞吐量的眾多變量信息。黃驊港集裝箱吞吐量預測算例表明，該方法能夠在歷史年份數據較少的情況下，精確度較高的預測集裝箱吞吐量，算例中給出的黃驊港集裝箱吞吐量2020年、2025年預測結果，也可為黃驊港發展建設預測提供參考。