基于安全域法的TCSC 優化配置
黃 堃,張 楠,奚茂龍
無錫職業技術學院控制技術學院,江蘇 無錫214121
在智能電網背景下,隨著以TCSC、SVC 為代表的可控FACTS 設備的不斷接入電網,電力系統的運行特性與潮流分布更加復雜多變[1,2],因此十分必要進行靜態安全域(Steady-state security region,SSSR)研究,以評估電網運行狀態、指導預防控制。
靜態安全域的思想最早在1975年由Hnyilicz等人提出,即為在給定的網絡結構下保證電力系統安全穩定運行的注入功率的集合[3]。對于輸電網較為關心的有功靜態安全域,目前研究重點考慮包括支路潮流約束與發電機節點的有功出力約束[3-5]。文獻[5]基于直流潮流模型,利用節點有功注入與支路相位差之間的線性關系,推得有功靜態安全域(Active Power SSSR,AP-SSSR)可以近似表示為節點有功注入空間上超平面圍成N維多面體。
作為最常見的FACTS裝置,TCSC可通過控制其等效電抗進而改變潮流分布,TCSC常用于進行潮流調整與提高系統小干擾穩定性[6-8]。由于TCSC對潮流分布特性具有重要影響,因此TCSC將不可避免影響系統有功靜態安全域,TCSC的配置對有功靜態安全域的影響,值得進一步分析和研究。
針對TCSC優化配置,現有文獻大多以提高電力系統傳輸能力和潮流分布均勻作為目標。文獻[9]建立了用于提高輸電能力的TCSC優化配置模型,并采用免疫算法進行求解。文獻[10]研究了靜態穩定與暫態穩定約束下的TCSC優化配置,結果表明TCSC優化配置后,系統傳輸能力得到了顯著提高。文獻[11]基于潮流熵研究了TCSC的優化配置,得到了良好的結果。目前未有文獻從靜態安全域的角度來研究TCSC的優化配置。
本文首先基于等效功率注入法對TCSC進行等效,進而推導得到計及TCSC影響的靜態安全域。在此基礎上,以TCSC等效電抗為優化變量,以靜態安全域的面積最大為優化目標,建立TCSC優化配置模型,采用遺傳算法對其進行求解。最后,以IEEE標準節點系統進行驗證分析。
1 有功靜態安全域法的基本原理
基于直流潮流模型[12],電力系統的有功潮流方程可簡化為:
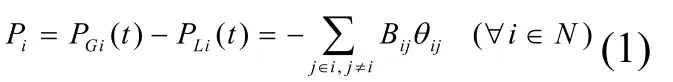
整理上式可得:

則流經支路d的有功潮流可以表示為節點有功功率注入的函數:
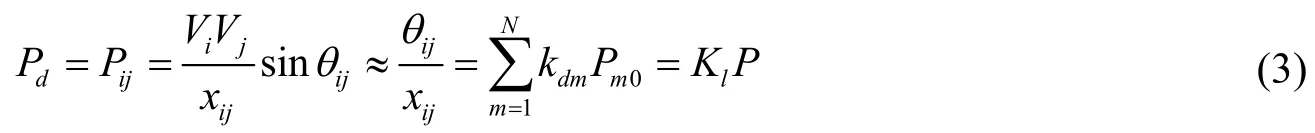
其中,
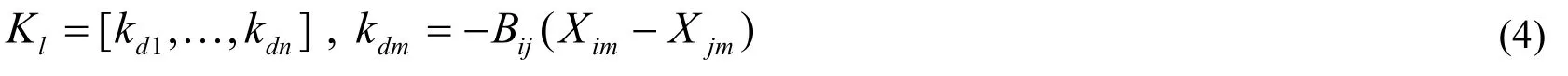
式中,Xim為電抗陣的第i行第m列元素;i、j分別為支路d兩端母線的編號。
則考慮支路d的輸送容量限制以及節點m的有功功率注入余數,則有功靜態安全域可表示為:

其中,Pm為節點m的注入有功功率。
2 計及TCSC 的有功靜態安全域
2.1 基于等效功率注入法對TCSC 進行等效
假設在線路l-m中靠近節點l端裝有TCSC,如下圖1所示。
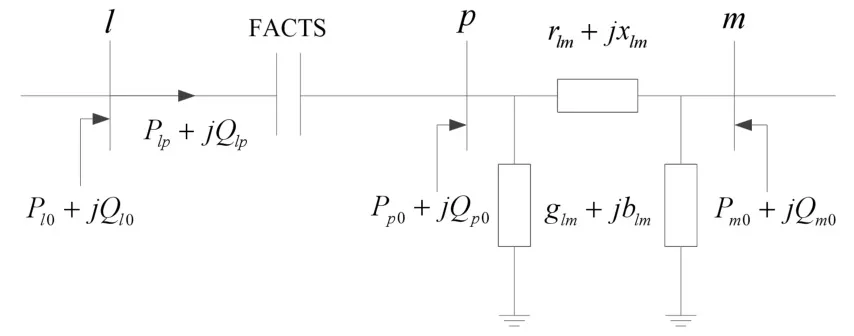
圖1 含TCSC 的系統Fig.1 The system with TCSC
基于等效注入功率法[13],將TCSC斷開并將流經原TCSC支路的潮流等效為兩個與TCSC等效電抗相關的節點注入功率,則圖1的等值模型如圖2所示。

圖2 等值模型Fig.2 Equivalent model
則流經TCSC支路(即支路l-p)的有功功率為:
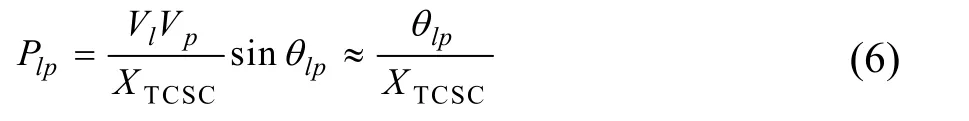
對于等值后的TCSC,節點l、p上的有功注入變化量分別如下所示,其中XTCSC為TCSC等效電抗。

2.2 計及TCSC 影響的有功靜態安全域
基于2.1節所述等效處理后,則節點l與節點p的注入有功功率分別修正為:
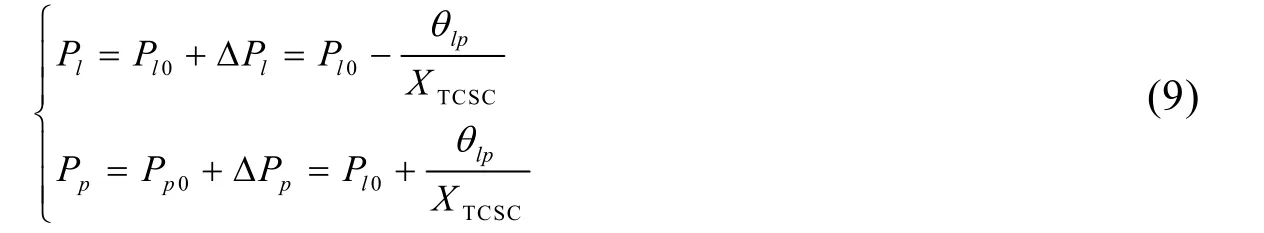
結合(3),可推導得到流經支路d的有功潮流為:
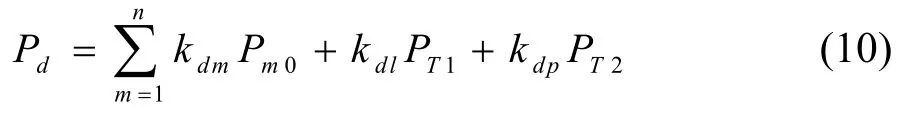
將式(9)代入式(10),則可進一步得到:
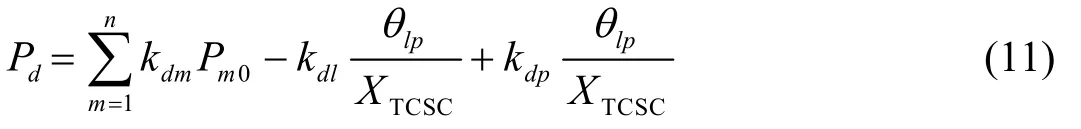
則根據式(2),可以得到TCSC支路兩端的電壓相位差為:
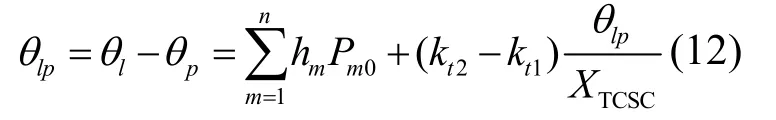
聯立式(11)與(12),則進一步得到:
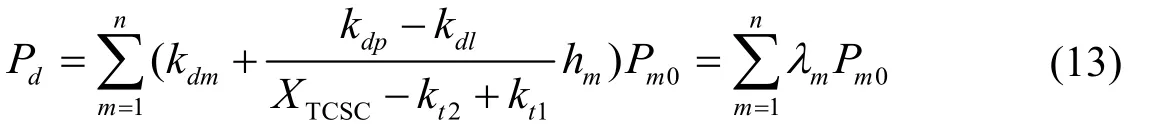
則考慮支路d的輸送容量限制以及節點m的有功功率注入余數,則計及TCSC影響的有功靜態安全域可表示為:

記有功靜態安全域的面積為A,即有:
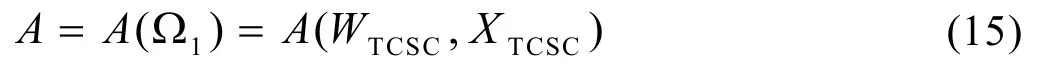
式中,WTCSC表示TCSC在系統中的安裝地點。進一步,定義有功靜態安全域面積指數,簡稱靜態安全域面積,如下式所示:
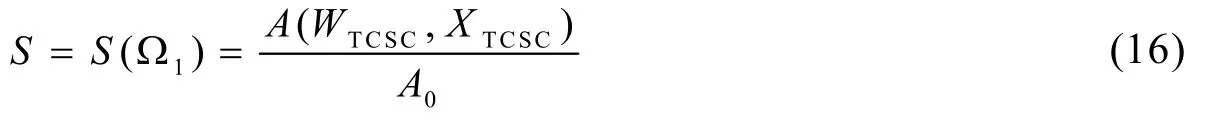
其中,A0表示系統未配置TCSC時的有功靜態安全域面積,有功靜態安全域的面積可以表示系統的靜態安全裕度。
3 基于遺傳算法的TCSC 優化配置
3.1 計及TCSC 影響的AP-SSSR 優化模型
3.1.1 優化變量 靜態安全域優化模型的優化變量取TCSC 的等效電抗與TCSC 的安裝位置。
3.1.2 目標函數 以系統靜態安全域面積最大為目標,其數學描述如下所示:
式中:F為目標函數;X=[WTCSC,XTCSC]為優化變量;gj(X)、hk(X)為等式、不等式約束函數;n1、n2為等式約束、不等式約束個數。
3.1.3 約束條件 建立約束條件是為了滿足電網安全穩定運行的基本要求,由等式約束和不等式約束構成。
1)忽略網損,系統功率平衡約束。

式中:PGi為第i臺發電機的有功出力,PL為系統負荷值,M為發電機組臺數。
2)發電機組出力約束。

式中:Pi-min、Pi-max分別為第i臺機組有功出力的上、下限。
3)TCSC的取值范圍即TCSC的串補度約束。
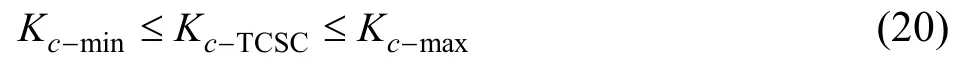
式中:Kc-TCSC為TCSC的串聯補償度,Kc-min、Kc-max為相應最小、最大串聯補償度。
4)TCSC安裝位置的約束。

式中:ΩTCSC表示TCSC在系統中可選安裝位置的集合。
3.2 基于遺傳算法求解協調優化模型
遺傳算法屬于人工智能算法,其通過模擬生物進化過程來搜索最優解,并且遺傳算法能適用于各種性質的目標函數(包括連續型與離散型函數),其流程圖如下圖3所示。本文采用遺傳算法對計及TCSC影響的AP-SSSR優化模型進行求解。
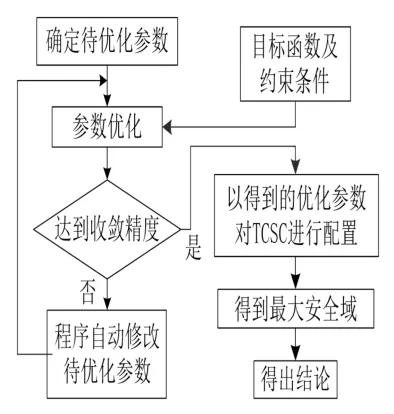
圖3 遺傳算法的流程圖Fig.3 Process of genetic algorithm
4 算例研究
對于上述所提方法,本文基于IEEE10 機39 節點標準系統進行仿真分析。
4.1 TCSC 對有功靜態安全域影響分析
為便于對比,選取30 號母線以及37 號母線上發電機有功出力PG30、PG37構成安全域二維空間,其他所有負荷及發電機按照標準參數計算,并以支路9~8 為對象構建靜態安全域。
當系統未配置TCSC時,并取式(14)中的參數為:Pm-min=0.5,Pm-max=8.0,Pd-min=0,Pd-max=0.6;則以PG30、PG37為坐標而構建的靜態安全域,其如圖4所示。
進一步研究TCSC安裝位置與等效電抗對安全域的影響,結果如圖5所示。支路編號1為支路1~2,支路編號2為支路1~39,支路編號3為支路2~3,支路編號4為支路2~25,支路編號5為支路3~4。
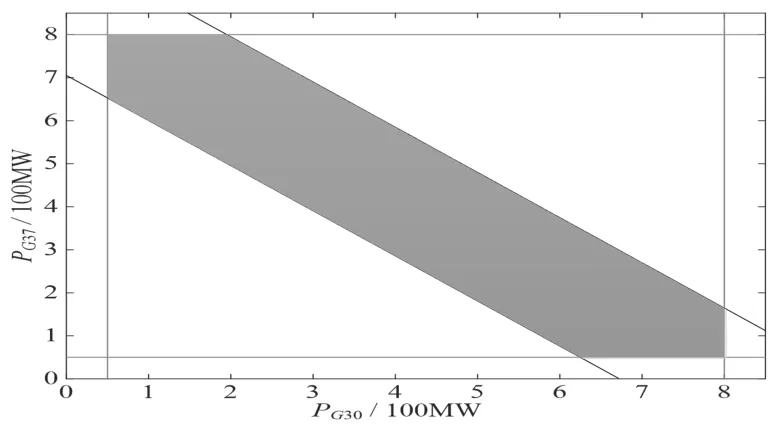
圖4 系統未配置TCSC 時的靜態安全域Fig.4 AP-SSSR without TCSC
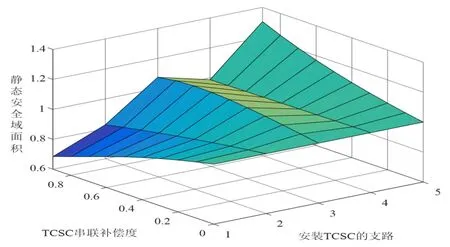
圖5 TCSC 安裝位置與等效電抗對安全域的影響Fig.5 Influence of TCSC installation position and equivalent reactance on AP-SSSR
通過分析以上結果,可得以下結論:1)TCSC 的串聯補償度(等效電抗)對靜態安全域的影響較為復雜,其影響特性與TCSC 的安裝位置密切相關。2)TCSC 的安裝位置對靜態安全域具有重要影響,當TCSC 位于不同位置時,系統的靜態安全域表現出顯著不同的特性。3)當TCSC 位于支路1~2 和支路1~39 時,隨著串聯補償度的提高,其靜態安全域面積逐漸下降;當TCSC 位于支路2~3時,隨著串聯補償度的提高,其靜態安全域面積先逐漸增加后逐漸下降;當TCSC 位于支路2~25 時,隨著串聯補償度的提高,其靜態安全域面積幾乎不變;當TCSC 位于支路3~4 時,隨著串聯補償度的提高,其靜態安全域面積逐漸增加。
4.2 TCSC 的優化配置
采用遺傳算法,以XTCSC=-0.0020 作為初始值,對TCSC 等效電抗進行優化,優化過程中,取最大迭代次數為25,優化的約束條件取值如表1 所示。則得到最優配置參數如表2 所示。

表1 優化的約束條件Table 1 Optimized constraints

表2 TCSC 的最優配置Table 2 Optimum configuration of TCSC
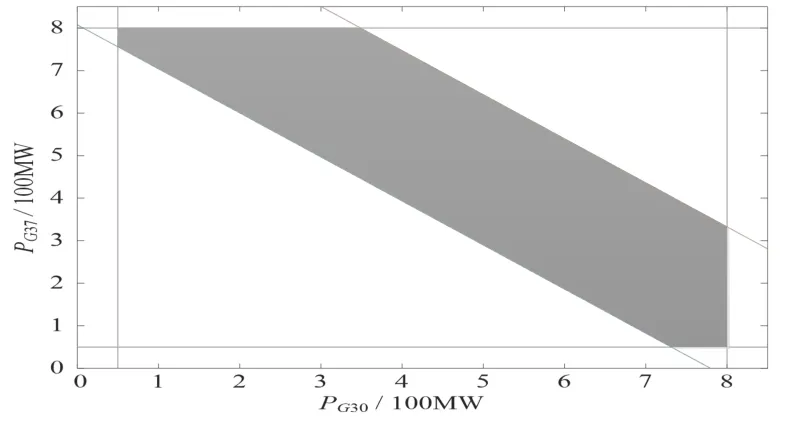
圖6 TCSC 固定于支路2~3 時的最大靜態安全域Fig.6 The max AP-SSSR when TCSC is fixed at branch 2~3
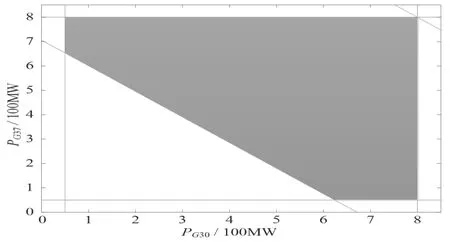
圖7 TCSC 為最優配置時的最大安全域Fig.7 The max AP-SSSR at optimal TCSC
根據表2,可知TCSC 經過優化配置,相應的靜態安全域面積都得到了顯著提高。當TCSC 固定于支路2~3 并且僅對TCSC 的等值電抗進行優化時,其最大的靜態安全域面積為1.0986,如圖6所示。而當同時對TCSC 的安裝位置與等值電抗進行優化時,即當安裝位置為支路8~9 且串聯補償度為0.7273 時,其最大的靜態安全域面積為1.9748,如圖7 所示。
5 結論
本文采用靜態安全域法研究了TCSC 的優化配置。基于等效功率注入法得到計及TCSC 影響的靜態安全域。并進一步建立TCSC 優化配置模型,采用改進模擬植物生長算法對其進行求解。最后,以IEEE 標準系統驗證了所提方法的有效性。可以得到以下結論:1)本文所提方法能夠較快地得到計及TCSC 影響的靜態安全域。2)TCSC 的等效電抗對靜態安全域的影響較為復雜,其影響特性與TCSC 的安裝位置密切相關。3)TCSC 的安裝位置對靜態安全域具有重要影響,當TCSC 位于不同位置時,系統的靜態安全域表現出顯著不同的特性。4)未來的工作里,將進一步研究多TCSC 以及安裝位置的協調優化以最大限度提高系統的靜態安全域。

