再談雙重有效應力
——對《雙重有效應力再認識及其綜合作用》一文的討論與分析

李傳亮，朱蘇陽

西南石油大學石油與天然氣工程學院，四川成都610599

0 引言

多孔介質就是帶有孔隙的固體，其中的孔隙并不是物質，而是多孔介質的存在形式。巖石、土壤、動植物機體等都是多孔介質。多孔介質本質上仍屬于固體，但因帶有孔隙，其力學性質又與普通(純)固體有著很大的差別，固體力學的許多理論都不能直接應用于多孔介質。為了應用固體力學的理論研究多孔介質的力學行為，人們提出了有效應力的概念[1]。有了有效應力作為橋梁和紐帶，固體力學的許多理論就可以應用于多孔介質了。因此，有效應力是多孔介質力學的基礎概念，整個多孔介質力學都是建立在有效應力基礎之上的，也可以說，沒有有效應力就沒有多孔介質力學。

但是，如何構建有效應力卻是一個十分復雜的問題，不同學者在不同條件下提出了不同的有效應力形式。K.Terzaghi(1923)針對疏松的土介質提出了第一個有效應力[1]，后人稱之為Terzaghi有效應力。Terzaghi有效應力催生了土力學的誕生，在水壩、電站、基礎工程等建設中發揮了積極的作用，K.Terzaghi也因此成為了世界21位著名的力學家之一[2]。

M.Biot(1941)提出了第二個有效應力[3]，后人稱之為Biot有效應力。Biot有效應力是對Terzaghi有效應力的修正，其他人對Terzaghi有效應力的修正與Biot類似，只是修正系數的取值不同而已。土力學和巖石力學是兩門重要的自然科學學科，屬于多孔介質力學的兩個重要分支。

筆者在深入研究了多孔介質的變形機制之后，于1999年提出了雙重有效應力的概念[4-5]。根據雙重有效應力理論，多孔介質存在兩種基本的變形方式：本體變形和結構變形；與之相對應，多孔介質存在兩個有效應力：本體有效應力和結構有效應力。雙重有效應力的提出，為多孔介質力學的發展起到了積極的推動作用：巖石強度條件分析得到了改進[6]，建立了巖石壓縮系數測量新方法[7-10]，巖石應力敏感評價方法得到了改進[11-12]，多孔介質的流變模型得到了改進[13]，油井壓裂過程中地層巖石的破裂壓力公式得到了統一[14-15]，許多奇妙的新理論都已在雙重有效應力的支撐下浮出了水面。

然而，有些人對雙重有效應力不夠理解，進而對其提出了質疑。洪亮博士曾撰文對其進行質疑[16]，筆者也進行了回應[17]。最近，毛小龍博士也撰文對其進行了質疑[18]，并提出了新的雙重有效應力，為了讓大家更好地理解多孔介質的雙重有效應力，筆者在此與毛小龍博士作如下商榷。

1 多孔介質的變形機制

根據形成方式可以把多孔介質分成兩大類[5]：一類是在已有固體中建造孔隙而形成的次生多孔介質(圖1)，另一類是由碎屑顆粒堆積而成的原生多孔介質(圖2)。它們的力學機制是一樣的，為了敘述方便，下面僅以原生多孔介質為研究對象。

圖1 次生多孔介質形成示意圖Fig. 1 Formation of secondary porous media

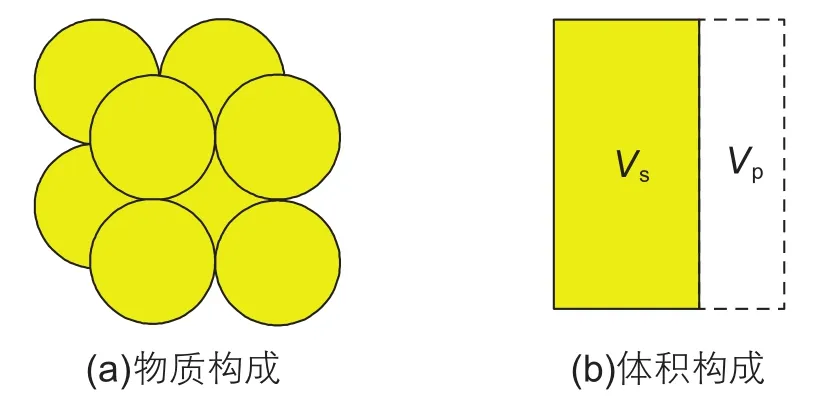
圖2 原生多孔介質構成圖Fig. 2 Composition of primary porous media

多孔介質的固體部分被稱作骨架，其余部分被稱作孔隙(空隙)。骨架顆粒有線元體、面元體和粒元體等多種復雜的幾何形態。孔隙的幾何形態也極其復雜，但大致可分為孔、洞、縫三種。多孔介質有3個體積：骨架體積、孔隙體積和外觀體積，而普通固體卻只有一個體積。圖2a為多孔介質的物質構成圖，圖2b為多孔介質的體積構成圖。

多孔介質的3個體積滿足下式

式中，Vs為骨架體積，m3；Vp為孔隙體積，m3；Vb為外觀體積，m3。

孔隙體積與外觀體積的比值，定義為多孔介質的孔隙度(空隙率)，即

式中，φ為孔隙度，小數。

孔隙度是多孔介質最重要的物性參數，它反映了多孔介質的孔隙發育程度和儲集能力。根據孔隙度的數值可以對多孔介質進行分類[19]：當φ＜0.3，為致密介質；當φ=0.3～0.9，為疏松介質；當φ＞0.9，為纖維介質。當φ=0，為純固體；當φ=1，為虛空。純固體和虛空為多孔介質的兩個極端。因此，孔隙度把多孔介質與普通固體統一了起來。

多孔介質的變形是通過骨架顆粒的變形和排列方式的改變來實現的。根據筆者的研究，多孔介質存在兩種基本的變形機制：本體變形和結構變形[4-5]。多孔介質的實際變形是這兩種基本變形的復雜組合。

1.1 本體變形

所謂的本體變形(primary deformation)，是指因骨架顆粒自身的變形而導致的介質整體變形。在本體變形過程中，骨架顆粒的排列方式并不發生變化，變化的是骨架顆粒自身的體積(圖3)。骨架顆粒的變形是由于顆粒自身的應力即骨架應力的變化所致。骨架應力決定介質的本體變形，介質的應力—應變關系為

式中，εp為多孔介質的本體應變，無因次；σs為多孔介質的骨架應力，MPa。

圖3 多孔介質的本體變形(可逆)Fig. 3 Primary deformation of porous media(reversible)

圖4 為本體變形過程中的體積變化。本體變形實際上就是介質的壓縮變形(compression)。

圖4 本體變形的體積變化(可逆)Fig. 4 Volume change of primary deformation(reversible)

1.2 結構變形

所謂的結構變形(structural deformation)，是指因骨架顆粒排列方式的改變而導致的介質整體變形。在結構變形過程中，骨架顆粒自身的體積并不發生變化，變化的是骨架顆粒的排列方式(圖5)。介質的變形量與骨架顆粒之間的相對位移即介質的結構變化有關，而骨架顆粒之間的相對位移是因顆粒之間接觸應力的變化所致。接觸應力決定介質的結構變形，介質的應力—應變關系為

式中，εs為介質的結構應變，無因次；σc為骨架顆粒之間的接觸應力，MPa。

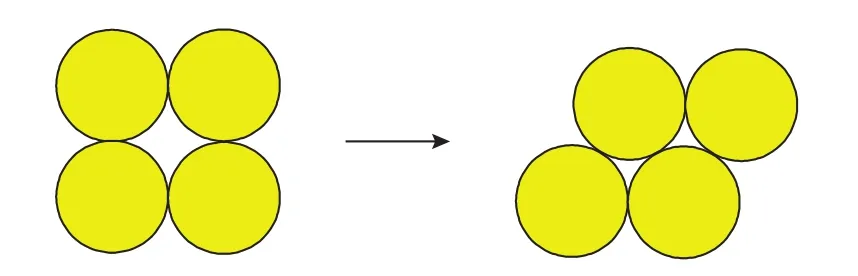
圖5 介質的結構變形(不可逆)Fig. 5 Structural deformation of porous media(irreversible)

圖6 為結構變形過程中的體積變化。結構變形實際上就是介質的壓實變形(compaction)。

介質的總應變為介質的本體應變與結構應變的代數和，即

式中，ε為介質的總應變，無因次。

圖6 結構變形的體積變化(不可逆)Fig. 6 Volume change of structural deformation(irreversible)

圖7 為介質的骨架應力和接觸應力示意圖，兩個應力之間不僅存在數值上的巨大差異，其性質也完全不同。一個為正，另一個可能為負。

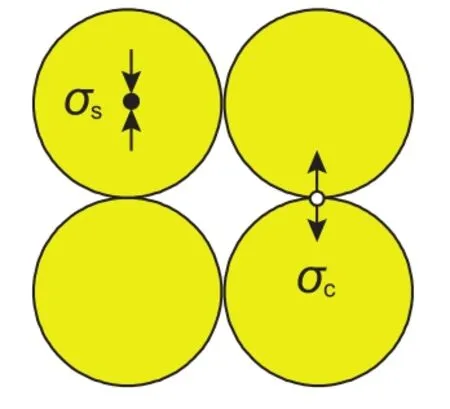
圖7 骨架應力和接觸應力Fig. 7 Skeleton stress and contact stress

介質的本體變形是由于骨架顆粒的變形所致，這種變形基本上屬于彈性變形，在應力卸除之后通常是可以恢復的，因而是可逆變形。介質的結構變形是由于介質的結構變化即骨架顆粒排列方式的改變所致，這種變形基本上屬于塑性變形，在應力卸除之后是不能恢復的，因而是不可逆變形。

疏松土介質的變形以結構變形為主，應力作用使顆粒由松散排列趨于緊湊排列，介質也由疏松狀態趨于致密狀態，與此同時，孔隙度也發生了巨大的變化。但是，應力卸除之后，顆粒的排列方式卻不能由緊湊排列恢復到松散排列，因而介質的結構變形是不可逆的。結構變形實際上是對介質的破壞，因為骨架顆粒的接觸處是應力最為集中的地方，也是最容易發生破壞的地方。

巖石一般屬于致密介質，致密介質的變形以本體變形為主，應力作用使巖石和巖石顆粒的體積受到壓縮；應力卸除，巖石和巖石顆粒的體積又發生膨脹，恢復到原始狀態，因而巖石的本體變形是一種可逆的彈性變形。巖石彈性變形過程中，骨架顆粒的排列方式并不發生變化(因顆粒已緊湊排列，并且膠結)，巖石的外觀體積、孔隙體積和骨架體積同步增大或縮小，因而巖石的孔隙度是不發生變化的(圖3)，這就是巖石本體變形過程中的孔隙度不變性原則[20]。

2 有效應力概念

普通固體受到應力的作用即產生變形，受拉即伸長，受壓即縮短(圖8)，固體的應力—應變曲線可以分成彈性變形和塑性變形兩個階段(圖9)。彈性變形是應力卸除后能夠恢復的變形，塑性變形是應力卸除后不能夠恢復的變形。當然，塑性變形階段也包含一定的彈性變形。彈性變形階段與塑性變形階段不是同時發生的，彈性變形一般為低應力作用階段，塑性變形一般為高應力作用階段。普通固體復雜的應力—應變關系可以分段進行研究，在彈性變形階段(σ＜σe)采用Hooke定律，即

式中，E為彈性模量，MPa；σ為應力，MPa；σe為彈性極限應力，MPa；ε為軸向應變，無因次。

在塑性變形階段(σ＞σe)很難用簡單公式進行描述，可以采用函數形式進行描述，即

彈性變形階段的應力—應變關系符合Hooke定律，相對比較簡單，塑性變形階段則相對比較復雜。

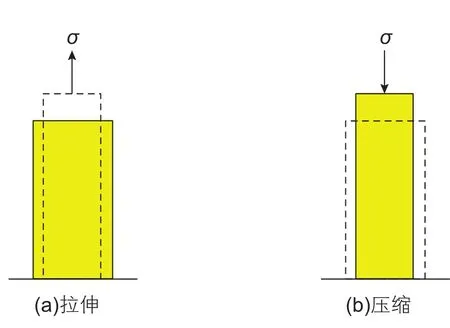
圖8 普通固體的變形Fig. 8 Deformation of ordinary solid

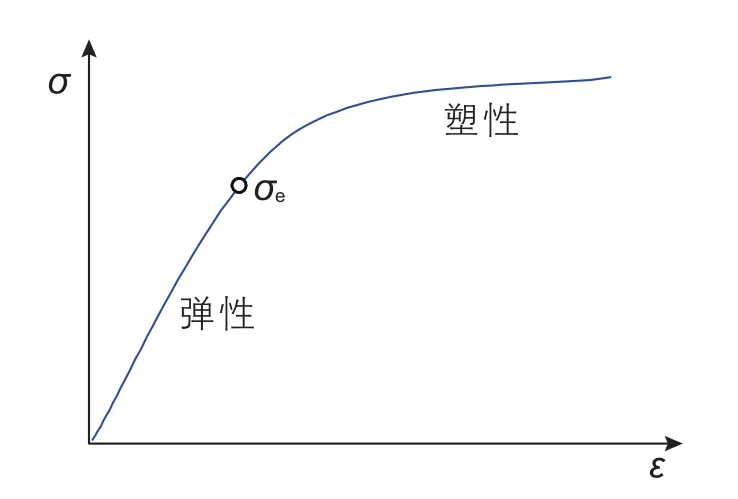
圖9 普通固體的應力—應變曲線Fig. 9 Curve of stress-strain of ordinary solid

普通固體在拉伸時變細，在壓縮時變粗，橫向應變與軸向應變的比值為泊松比，即

式中，ν為泊松比，無因次；εr為橫向應變，無因次。

由式(6)和式(7)可以看出，普通固體的復雜變形規律用一個應力分段進行研究即可，不需要借助于有效應力。但是，多孔介質不是普通固體，而是帶有孔隙的固體，其物質結構和受力狀態都比普通固體復雜。多孔介質的孔隙中通常飽和著流體(油、氣、水)，且同時受到外應力(外壓)和內應力(內壓)的共同作用(圖10a)。因此，多孔介質的變形是內、外兩個應力共同作用的結果，即

式中，σ為介質外壓，MPa；p為介質內壓，MPa。

圖10 多孔介質受力圖Fig. 10 Force diagram of porous media

若能找到式(9)的函數關系，則可以直接研究多孔介質的變形行為，不需要借助于有效應力。遺憾的是，迄今為止人們尚未找到式(9)的函數關系，不得不借助于有效應力。

所謂的有效應力，是為了工程計算方便而虛擬的應力概念，它單獨作用于多孔介質所產生的效果與內、外兩個真實應力共同作用所產生的效果完全相同，因此是一個等效應力(圖10b)。當材料的物質結構和應力狀態十分復雜時，有效應力就能發揮很好的作用。若找到了有效應力，則式(9)可以寫成

式中，σeff為有效應力，MPa。

固體力學的Hooke定律式(6)，則可以用有效應力來研究多孔介質的彈性變形

有效應力并不是真實應力，而是虛擬應力，不能進行實測，只能通過某種方法進行計算。構建有效應力的基本思想是：外壓的作用導致介質的壓縮，內壓的作用導致介質的膨脹，內、外壓對多孔介質產生的作用正好相反(圖10a)，因此，只需把內壓的作用從外壓中扣除，即可得到有效應力。但是，從外壓中扣除多少內壓，是一個需要研究的問題。

3 Terzaghi有效應力

1923年，K.Terzaghi針對疏松的土介質，通過實驗提出了第一個有效應力[1]，即Terzaghi有效應力

很顯然，Terzaghi有效應力為外應力與內應力的簡單差值，即從外壓中直接減去內壓。Terzaghi有效應力在地質科學及石油工程中被稱作有效上覆壓力，在室內巖心分析實驗中被稱作凈圍壓。圖11為Terzaghi實驗模型，該模型用彈簧模擬土介質的固體骨架，模型中充滿水。對模型施加外壓，模型即變形，模型的變形量可以用來計算彈簧的受力大小，模型的內壓用側邊水柱高度進行測量。

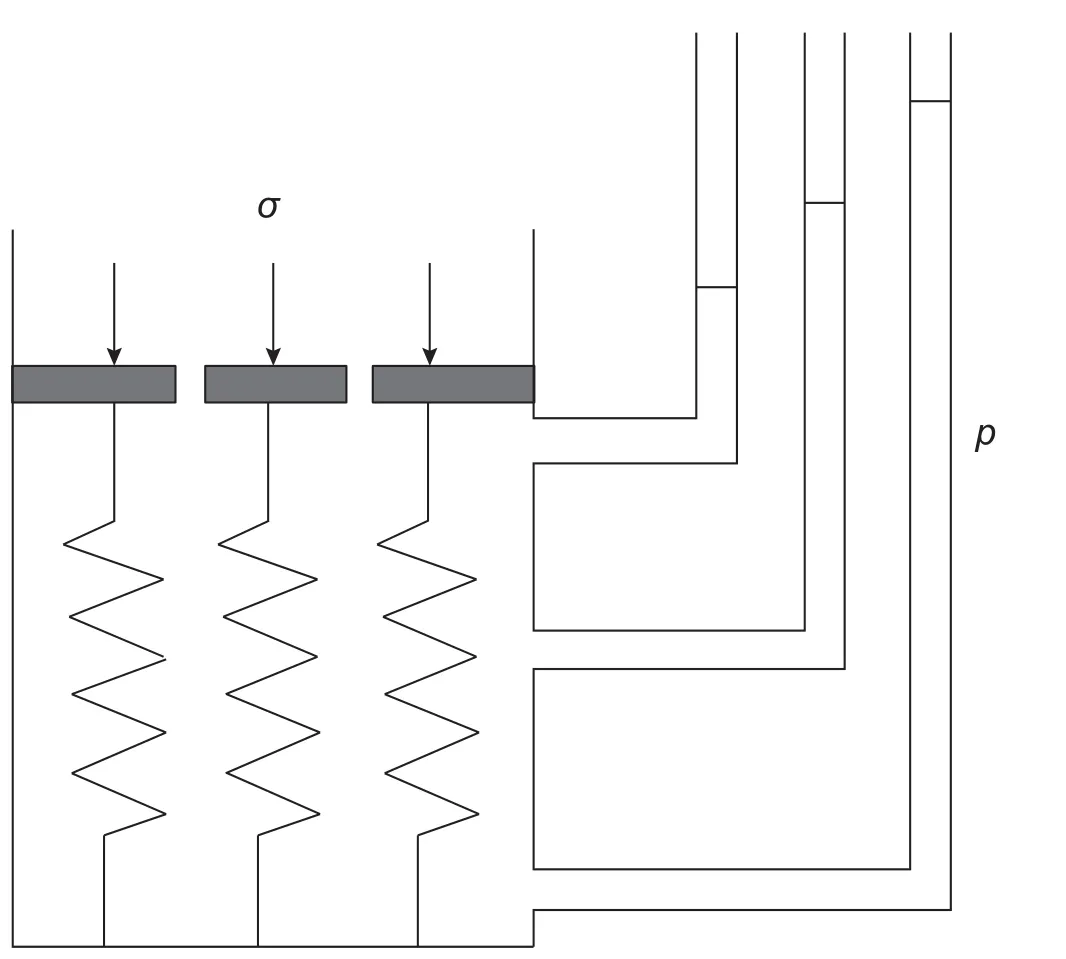
圖11 Terzaghi實驗模型Fig. 11 Terzaghi's experimental model

Terzaghi實驗是一個簡單而偉大的實驗，實驗的結果顯示外應力等于流體壓力與彈簧受力之和，進而導致了Terzaghi有效應力的建立。

然而，Terzaghi實驗存在的主要問題是，模型的骨架含量太少，即孔隙度太高，以至于內壓與外壓的作用面積幾乎相等。該模型沒有模擬到疏松土介質和致密巖石的性質，只近似模擬了纖維介質的性質。

關于Terzaghi方程的理論推導，通常采用圖12中的物理模型[1]，在該模型上建立靜力平衡方程，即

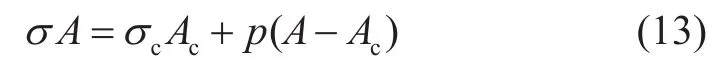
式中，A為外壓作用面積，m2；Ac為顆粒接觸面積，m2；σc為顆粒接觸應力，MPa。

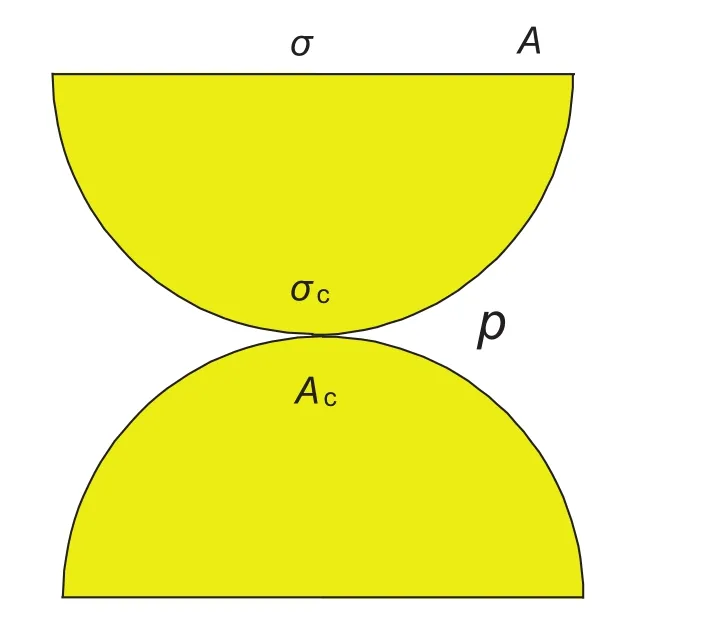
圖12 Terzaghi公式推導物理模型Fig. 12 Physical model for deduction of Terzaghi's equation

式(13)可以寫成

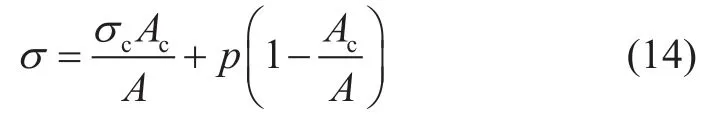
通常假設Ac特別小，于是很容易由式(14)導出Terzaghi公式(12)。

上面的公式推導中存在兩個問題，一是圖12中的σ并不是多孔介質的外應力，而是骨架顆粒內部的應力，是不可測量的；二是“Ac特別小”的假設在很多情況下并不成立，尤其是對于致密介質更是如此。

雖然Terzaghi有效應力的提出為土力學的誕生奠定了基礎，Terzaghi也因此為土力學的發展做出了不朽的貢獻。但是，Terzaghi有效應力并不適用于致密介質，這就為Terzaghi有效應力在長期的工程應用中出現的各種偏差埋下了伏筆。

Terzaghi有效應力的根本問題是，從外應力中扣除內應力時扣多了，因為內應力的作用面積遠小于外應力(圖10a)。而且，人們也不知道Terzaghi有效應力到底決定介質的本體變形，還是結構變形，它不能同時決定兩種變形。

4 Biot有效應力

為了消除Terzaghi有效應力在工程應用中的不適應性，許多人都對其進行了修正[5,21]，其中以Biot修正式應用最多，M.A.Biot于1941年提出的修正式為[3]

式中，α為Biot系數，無因次。

由式(15)計算的有效應力，被稱作Biot有效應力。式(15)中的修正系數一般稱為Biot系數，也叫有效應力系數。很多人對Terzaghi公式進行了修正，修正方法與Biot類似，只是修正系數的取值不同而已[22-35]。Biot有效應力的應用非常廣泛，但是，Biot系數沒有明確的物理意義，必須通過實驗測量或經驗方法加以確定。多數實驗測量的Biot系數在0～1，也有大于1或小于0的極端情況出現。Biot系數大于1，表明介質會自行膨脹；Biot系數小于0，表明介質會自行收縮。大于1和小于0都是錯誤的實驗結果。即使實驗測量的Biot系數在0～1，也不能說明實驗結果就是正確的，因為0.1與0.9的差別依然很大，實驗誤差難以克服。

A.W. Skempton(1960)[24]和J.Geestma(1957)[35]給出了Biot系數的理論公式，即

式中，cs為骨架顆粒(對骨架應力)的壓縮系數，MPa-1；cb為介質外觀體積(對外應力)的壓縮系數，MPa-1。

不僅外觀體積的壓縮系數不好測量，骨架顆粒的壓縮系數也不好測量，因為骨架顆粒的組成十分復雜，也不好把骨架物質從多孔介質中分離出來單獨進行實測。因此，很少有人采用式(16)來確定Biot系數。由于Biot系數存在很大的不確定性，大多數情況下人們都取經驗值，Biot有效應力公式在實際應用中也就成了一個經驗公式。

由于Biot系數通常小于1，相對于Terzaghi有效應力而言，Biot有效應力在從外應力中扣除內應力時少扣了一些，這算是一個進步。與Terzaghi有效應力相同的是，人們依然不知道Biot有效應力到底決定介質的本體變形，還是結構變形，它不可能同時決定兩種變形。

5 雙重有效應力

與多孔介質的兩種基本變形機制相對應，多孔介質存在兩個有效應力：本體有效應力和結構有效應力[4-5]。本體有效應力決定介質的本體變形，研究介質的本體變形行為時，應采用本體有效應力。結構有效應力決定介質的結構變形，研究介質的結構變形行為(包括介質的破壞)時，應采用結構有效應力。

5.1 本體有效應力

多孔介質除受到外應力σ和內應力p的作用之外，在連續介質意義上任意一點還存在骨架應力σs。但是，骨架應力并不是獨立存在的，它是內、外應力共同作用的結果，即σs是σ和p的函數。根據式(3)，介質是否產生本體變形，取決于σs的數值，與σ和p的數值大小沒有直接的關系。因此，只要知道了σs的數值，就能夠確定介質的本體變形行為。然而，σs是不可測量的，它必須通過一定的公式進行計算。

圖13為介質剖面圖，任一截面OO′面上方的外應力為σ，外應力的作用面積為A，因此，介質受到的總外力為σA。

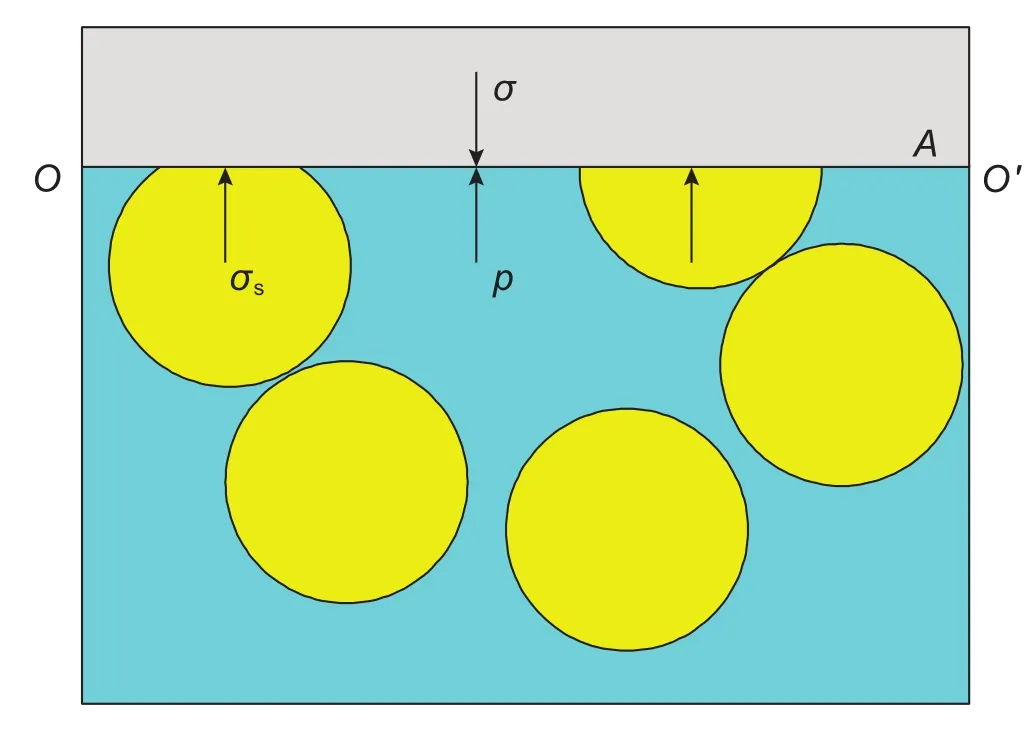
圖13 多孔介質應力關系圖(I)Fig. 13 Stress relationship of porous media(I)

OO′面下方的骨架應力為σs，骨架應力的作用面積為(1-φ)A，骨架對OO′面的總作用力為σs(1-φ)A。

OO′面下方的孔隙壓力為p，孔隙壓力的作用面積為φA，孔隙中流體對OO′面的總作用力為pφ A。

根據靜力平衡原理，OO′截面的上、下作用力相等，即

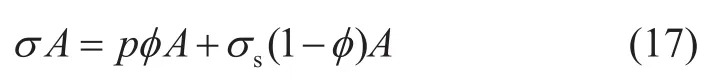
把式(17)整理之后，得

式(18)就是多孔介質的應力關系方程[36]。

由式(18)可以求出骨架應力的數值，再把骨架應力折算到整個介質橫截面積之上，即得本體有效應力計算公式

式(19)為本體有效應力的計算公式，本體有效應力的定義式為

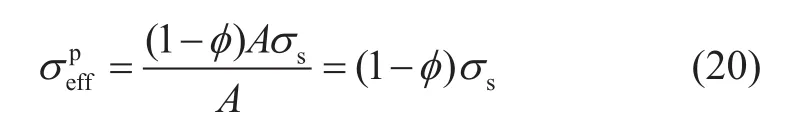
5.2 結構有效應力

接觸應力決定介質的結構變形，為了確定介質的結構變形量，必須首先計算出介質的接觸應力數值。

多孔介質骨架顆粒之間的接觸應力σc不是獨立存在的，它是內、外應力共同作用的結果，即σc是σ和p的函數。根據式(4)，介質是否產生結構變形，取決于σc的數值，與σ和p的數值大小沒有直接的關系。因此，只要知道了σc的數值，就能夠確定介質的結構變形行為。然而，σc也是不可測量的，它必須通過一定的公式進行計算。

圖14為介質剖面圖，任一截面OO′面上方的外應力為σ，外應力的作用面積為A，因此，介質受到的總外力為σA。

有了本體有效應力，多孔介質的本體應變量即可由下式計算

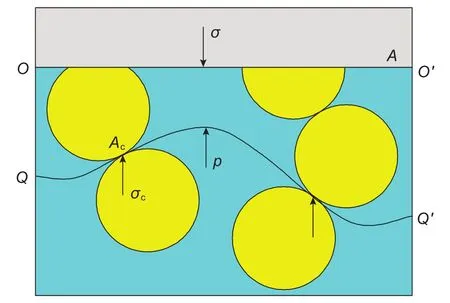
圖14 多孔介質應力關系圖(II)Fig. 14 Stress relationship of porous media(II)

QQ′面下方的孔隙壓力為p，孔隙壓力的垂向作用面積為φcA，孔隙中流體對QQ′面的總作用力為pφcA。

令QQ′面趨于OO′面，根據靜力平衡原理，OO′面的上方作用力與QQ′面的下方作用力相等，即

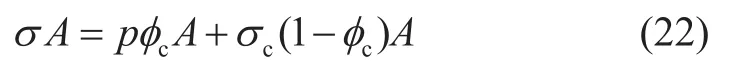
介質中任一連接骨架顆粒接觸點的曲面QQ′面下方的垂向接觸應力為σc，垂向接觸應力的作用面積為(1-φc)A，垂向接觸應力對QQ′面的總作用力為σc(1-φc)A。

把式(22)整理之后，得

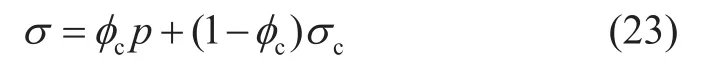
由式(23)可以求出接觸應力的數值，再把接觸應力折算到整個介質橫截面積之上，即得結構有效應力的計算公式

式(24)是結構有效應力的計算式，結構有效應力的定義式為

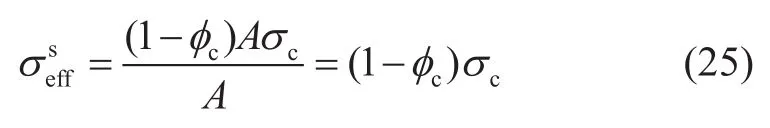
有了結構有效應力，多孔介質的結構應變量即可由下式計算

5.3 有效應力界限

結構有效應力計算公式(24)中的φc為介質的觸點孔隙度，它與介質的膠結系數滿足下式

式中，φc為介質的觸點孔隙度，小數；δc為介質的膠結系數，小數。

δc反映了介質的膠結程度，其計算公式為

式中，Ac為QQ′面上骨架顆粒接觸面積的垂向投影面積，m2；A為QQ′面上介質總面積的垂向投影面積，m2。

介質的膠結程度用膠結系數來衡量，而膠結強度則用拉伸應力強度來衡量。

不同介質的膠結程度差別很大[37]，點式接觸的介質沒有膠結物，膠結程度為0(圖15a)，觸點孔隙度也最大，為100%；基底膠結的膠結程度最高，為100%(圖15c)，觸點孔隙度也最小，為0；孔隙膠結的膠結程度和觸點孔隙度介于二者之間(圖15b)。

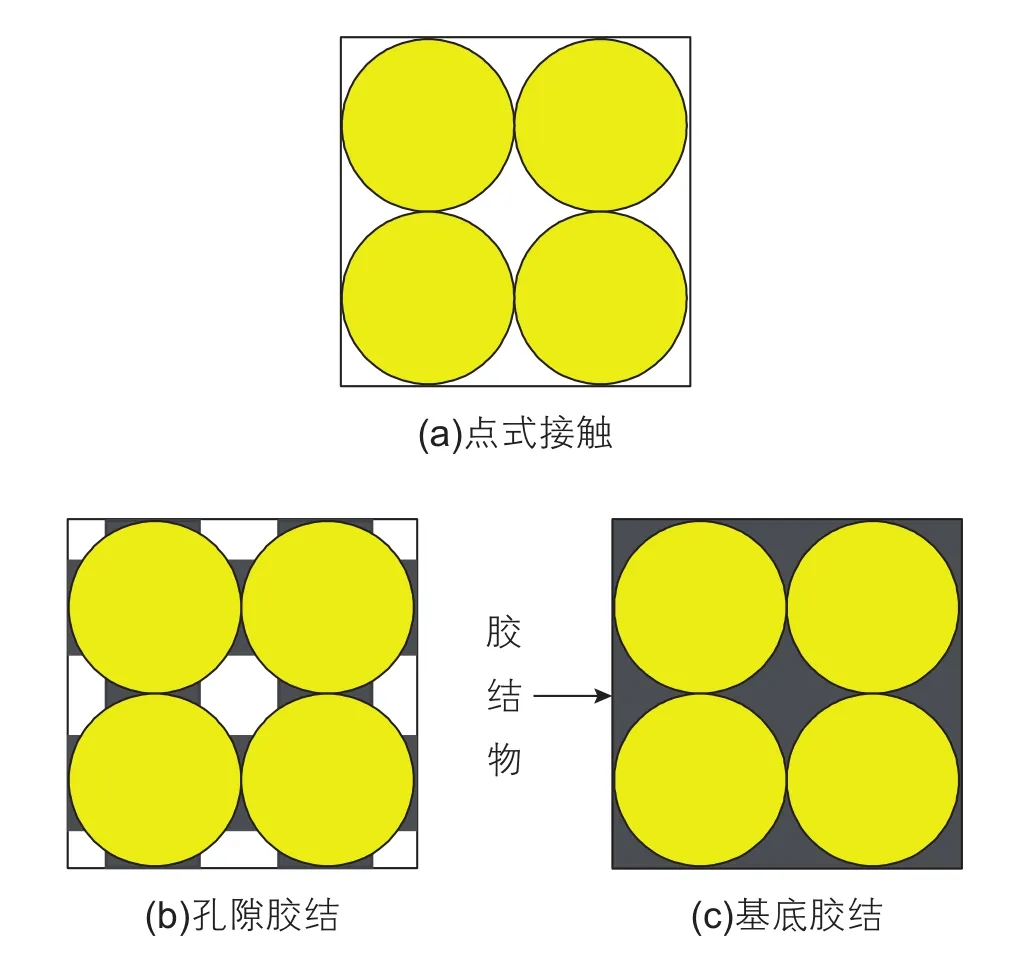
圖15 多孔介質膠結類型及膠結程度Fig. 15 Cementing types and cementing degree of porous media

本體有效應力計算公式(19)中的孔隙度φ，為介質的本體孔隙度。

很顯然，觸點孔隙度的數值大于本體孔隙度，但仍然小于 1，即φ＜φc＜1。

當φc→0，φ→0，表明介質的孔隙特征消失，介質趨于普通固體，此時，本體有效應力和結構有效應力皆趨于介質的外應力(圖16)。這也是普通固體不采用有效應力的原因。

當p→0，表明介質中無承壓流體，此時，本體有效應力和結構有效應力也趨于介質的外應力(圖16)。介質中不飽和流體，也就相當于普通固體，也無需采用有效應力。

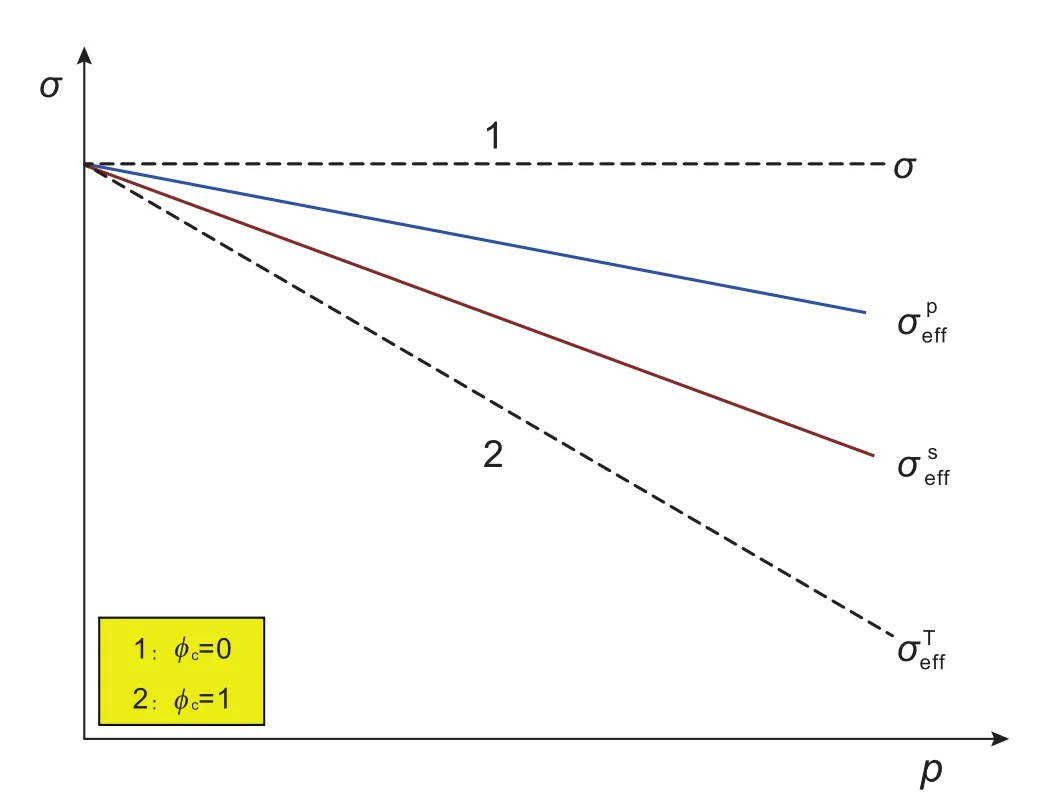
圖16 應力及有效應力關系圖Fig. 16 Relationship of stress and effective stress

當φc→1，表明介質趨于極度疏松，此時，結構有效應力公式趨于Terzaghi有效應力，即式(12)。

本體有效應力和結構有效應力合稱為多孔介質的雙重有效應力，它適用于所有的介質類型。由于多孔介質會同時產生本體變形和結構變形，因此雙重有效應力需同時使用。對于以產生結構變形為主的疏松土介質，結構有效應力的應用相對多一些。對于以產生本體變形為主的致密巖石，本體有效應力的應用相對多一些。

雙重有效應力與Terzaghi有效應力以及介質內、外應力之間的關系如圖16所示。由圖中曲線可以看出，外應力是雙重有效應力的上限值，而Terzaghi有效應力是雙重有效應力的下限值。

很顯然，Terzaghi有效應力為結構有效應力的極限值，它只適用于極其疏松的多孔介質(φc=1)，而且也只能用于研究多孔介質的結構變形或破壞行為。但是，Terzaghi有效應力并不適用于巖石，因為巖石屬于致密介質。事實上，φc=1的多孔介質是不存在的，即使是疏松的土介質，φc也小于1，這就為Terzaghi有效應力在長期的工程應用中出現的各種偏差埋下了伏筆。

Terzaghi有效應力在工程應用中的不適應性可通過圖17中的“思想實驗”加以證明[5]。圖17中的密閉容器中放置了一塊巖石。當把圖17a中的低壓(1 MPa)升高至圖17b中的高壓(100 MPa)時，巖石產生了明顯的本體變形(壓縮)。但圖17a中巖石的Terzaghi有效應力為0，圖17b中巖石的Terzaghi有效應力亦為0，二者完全相等。根據有效應力原理，巖石的變形是由有效應力的變化所致，圖17中的巖石產生了明顯的變形，而Terzaghi有效應力并沒有發生任何變化，顯然，巖石的變形與Terzaghi有效應力無關。

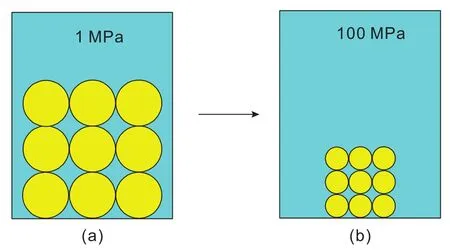
圖17 密閉容器中巖石壓縮圖Fig. 17 Compression of rock in a closed container

但是，根據本體有效應力計算公式(19)，圖17a中巖石的本體有效應力為0.52 MPa，圖17b中巖石的本體有效應力為52.36 MPa。本體有效應力的大幅度提高，導致了巖石的本體變形。圖17中巖石的顆粒排列方式為立方體排列，孔隙度為47.64%。

雙重有效應力通過孔隙度把普通固體與多孔介質統一了起來，有效應力計算公式中的孔隙度(包括觸點孔隙度)反映了孔隙壓力對有效應力的貢獻權值。雙重有效應力反映了多孔介質的物質結構特征，而Terzaghi有效應力則忽視了多孔介質的物質結構，把內、外應力同等對待，顯然是不夠科學的。

K.Terzaghi因提出了Terzaghi有效應力而推開了多孔介質力學的大門。在Terzaghi有效應力的旗幟下，誕生了土力學和巖石力學兩門重要的自然科學學科。然而，Terzaghi有效應力的應用范圍是十分有限的，它只近似適用于極其疏松的多孔介質。Biot有效應力公式是一個經驗公式，應用過程不確定性很大，物理意義不明確。在經歷了Terzaghi有效應力和Biot有效應力兩個發展階段之后，雙重有效應力的提出又為多孔介質力學的發展起到了積極的推動作用。

6 雙重有效應力有何問題？

毛博士在評論筆者提出的雙重有效應力時說[18]：“然而，兩個有效應力表達式與Biot、Bishop等學者早期提出的兩個有效應力表達式相同，而這兩個表達式與1955年Laughton經典鉛粒高壓實驗相矛盾，在60年代后被逐漸棄用，Skempton、Biship等人提出的有效應力表達式則漸漸被接受。”

毛博士的這個說法顯然與事實不符，雙重有效應力由本體有效應力和結構有效應力構成，本體有效應力為式(19)，結構有效應力為式(24)，這兩個公式與Biot有效應力公式(15)有相同的地方嗎？

毛博士論文中沒有給出Bishop有效應力的表達式，Bishop有效應力是針對未飽和土介質提出的，其公式為[38]

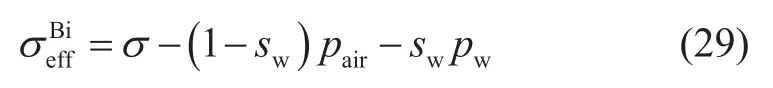
所謂的未飽和土，是指沒有被水完全飽和的土，土中含有一部分空氣，空氣壓力與水相壓力的飽和度加權平均值就是孔隙中的流體壓力，也就是Terzaghi有效應力公式(12)中的孔隙壓力p。因此，Bishop有效應力就是Terzaghi有效應力的簡單變形，算不上一個獨立的有效應力。

對比一下不難發現，筆者提出的本體有效應力式(19)和結構有效應力式(24)，沒有一個是與Bishop有效應力公式相同的。

毛博士說[18]：“Biot和Bishop兩個有效應力在60年代后被逐漸棄用，Skempton、Biship等人提出的有效應力表達式則漸漸被接受”。這個說法也是不符合事實的，Biot有效應力目前仍廣泛應用于土力學和巖石力學中。毛博士所說的Biship有效應力應該是誤用，其實并沒有這個有效應力。

K.Terzaghi是土力學的奠基人，他推動建立了“國際土力學及基礎工程”協會，并一直擔任主席職務。Terzaghi于1963年去世后該協會主席職務就由Biot接任。Biot是繼Terzaghi之后對多孔介質力學做出杰出貢獻的第二號人物。在Biot長期擔任國際土力學及基礎工程協會主席職務期間，Biot有效應力不可能被棄用。

毛博士說Skempton有效應力正逐漸被接受。所謂的Skempton有效應力，其實就是把Biot有效應力公式(12)中的Biot系數固定為式(16)的一個特定值[24]，即

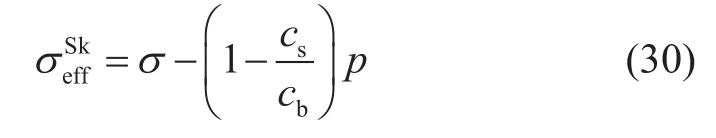
式中，為Skempton有效應力，MPa。

實際上，Skempton有效應力也包含在Biot有效應力之中，算不上一個獨立的有效應力，只是Biot有效應力的一個特例，實際應用并不多，因為外觀體積和骨架體積的壓縮系數都不好測量。

毛博士試圖用圖17中的思想實驗證偽筆者的雙重有效應力。毛博士說[18]：“對于完全浸沒在靜水壓中的多孔介質，無論其微觀顆粒間接觸面積和孔隙度為多少，多孔介質各處所受應力均為p。其微觀顆粒和宏觀整體都在應力p下均勻壓縮，本體有效應力應為p，無顆粒間變形或結構變形，結構有效應力應為0”。“這與本體有效應力應為p、結構有效應力為0的實際情況不一致，顆粒等效平均應力、顆粒間等效平均應力大小均不能決定本體變形和結構變形大小，需要重新認識。”毛博士說的顆粒等效平均應力就是筆者提出的本體有效應力，顆粒間等效平均應力就是筆者提出的結構有效應力。

毛博士為何認為圖17中的本體有效應力應該為p呢？實際上，圖17中的骨架應力為p，骨架應力不是本體有效應力，骨架應力折算到整個介質橫截面積上之后才是本體有效應力，因此，圖17的本體有效應力為(1?φ)p，而不是毛博士說的為p。本體有效應力決定介質的本體變形，即介質的壓縮變形。只要存在本體有效應力，介質就會被壓縮，即出現本體變形。本體有效應力與本體變形之間存在對應關系。圖17解釋了介質的本體變形機制。毛博士的“顆粒等效平均應力大小不能決定本體變形大小”的說法是不成立的。

圖17中的結構有效應力為(1?φc)p。毛博士認為圖17沒有發生結構變形，就不應該有結構有效應力或結構有效應力應該為0。所謂的結構變形，其實就是介質的破壞，也就是圖9中的塑性變形。圖9中只要有應力存在，就有彈性變形，但不一定有塑性變形。只有當應力超過彈性極限應力時，才會出現塑性變形。圖17中存在結構有效應力，而沒有出現結構變形，是因為結構有效應力還沒有達到極限應力。因此，毛博士的“顆粒間等效平均應力大小不能決定本體變形和結構變形大小”的說法也是不成立的。

毛博士還用Laughton的鉛粒高壓實驗結果來否定筆者的雙重有效應力[18]：“此外，顆粒等效平均應力和顆粒間等效平均應力表達式分別與孔隙度、顆粒間接觸面積有關，而1955年Laughton經典鉛粒高壓實驗表明：改變總應力和流壓，無論顆粒接觸面積為0.03、0.11還是0.95，孔隙度為0.4、0.31還是0.03，鉛粒多孔介質有效應力系數(即Biot系數)均接近于1，其有效應力與孔隙度、接觸面積均無直接關系，這也說明舊雙重有效應力存在問題。”

如果毛博士認為Laughton的實驗結果是正確的，繼續研究有效應力就沒有意義了，因為不管什么樣的多孔介質，Biot系數均接近于1，直接使用Terzaghi有效應力就可以了，還研究其他的有效應力干什么呢？孔隙度為3%的致密介質與孔隙度為40%的疏松介質，外應力與內應力對介質的作用是完全等價的，這不就忽視了多孔介質的物質結構了嗎？如果孔隙度為0，介質中沒有流體了，也就沒有孔隙壓力了，還要繼續采用Terzaghi有效應力研究多孔介質的力學行為嗎？毛博士論文中的“顆粒接觸面積為0.03、0.11還是0.95”是什么意思？

表1為Laughton的實驗結果[18]，Biot系數出現了大于1的情況，可以判斷實驗結果是不正確的，因為多孔介質將出現自行膨脹的現象，即在外壓與內壓相同的情況下，介質的有效應力為負值，介質不僅沒有被壓縮，還會莫名其妙的膨脹變大，成了圖17中壓縮過程的逆過程。表1中小于1的數值也普遍偏高。

7 新雙重有效應力質疑

毛博士在否定了筆者的雙重有效應力之后，又提出了他自己的雙重有效應力，并命名為新雙重有效應力[18]，而把筆者提出的雙重有效應力稱之為舊雙重有效應力。實際上，毛博士的新雙重有效應力存在很大的問題，下面對其進行分析。

7.1 新結構有效應力

毛博士從圖17的思想實驗中得出[18]，“在靜水壓中，顆粒均勻受力，顆粒間真實平均應力為p，但結構變形為0，這說明于顆粒間真實平均應力p并不會引起顆粒間變形。顆粒間作用力中至少有一部分用來平衡流壓p，這部分應力與孔隙流壓共同作用，均勻壓縮顆粒從而不產生結構變形；只有平衡流壓之外的凈應力集中作用在顆粒接觸面上產生額外的偏應力，從而引起顆粒間滑動變形，產生介質結構變形。即引起顆粒間變形的真正有效的應力為超出平衡孔隙流壓之外的顆粒間應力。”于是，毛博士定義了新結構有效應力，本文稱之為毛氏結構有效應力，即

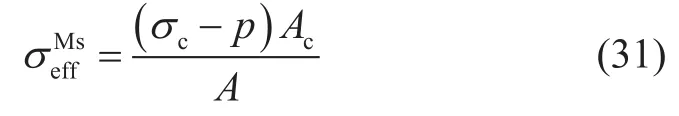
把式(23)代入式(31)，得毛氏結構有效應力的計算公式

由式(32)可以看出，毛氏結構有效應力其實就是Terzaghi有效應力。

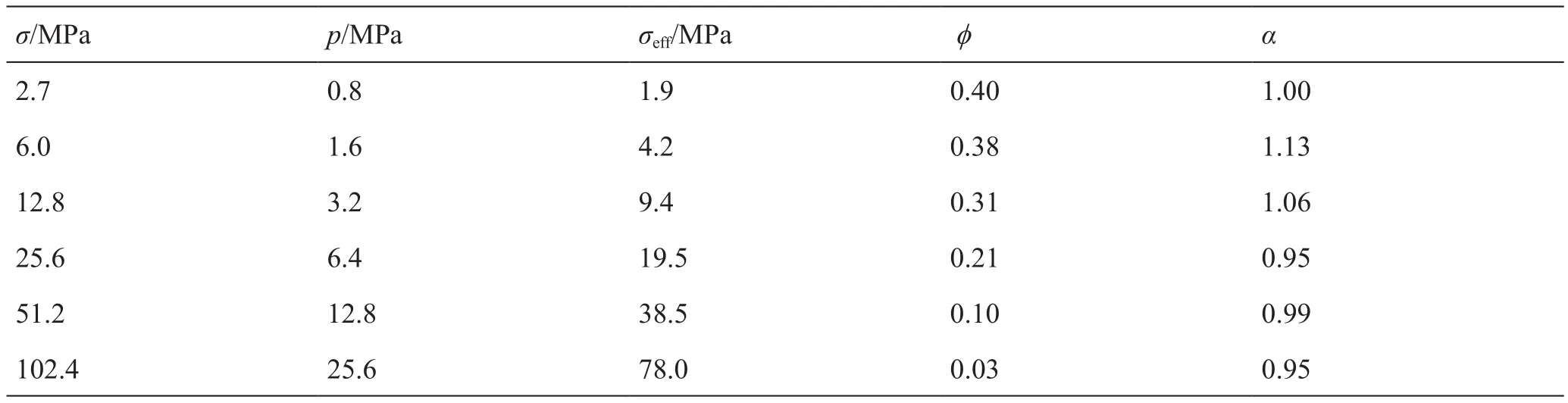
表1 鉛粒高壓測試結果Table 1 High pressure test results of lead shot

很顯然，毛博士認為顆粒之間的接觸應力數值中，超出孔隙壓力的部分才能產生結構變形，若接觸應力等于或小于孔隙壓力，則不能產生結構變形。這個觀點實際上是不成立的。若介質為膠結巖石，超出孔隙壓力的接觸應力也不會產生結構變形，測量巖石壓縮系數的過程就是如此，因為一旦顆粒間產生滑動(結構變形)，巖石就碎了。地層條件下巖石的接觸應力基本上都大于孔隙壓力，也沒發現巖石都是碎的，而通常都是完整成形的。

如果接觸應力等于孔隙壓力，就不產生結構變形了嗎？當然也不是。如果圖17中的多孔介質是疏松的干土樣，往里面注水，土樣就會沉陷固結，即出現了結構變形，很多土壤下雨后出現的變形就屬于這種情況。

如果接觸應力小于孔隙壓力，也是會產生結構變形的。壓裂時往地層巖石里注入高壓流體，孔隙壓力不斷升高，而接觸應力不斷減小，當接觸應力小到負值并到達破裂極限時，地層就產生裂縫了，即出現了結構變形。

因此，多孔介質在什么情況下產生結構變形，并不唯一地取決于結構有效應力的數值，還同時取決于介質本身的性質。

通常上面的分析不難看出，毛氏結構有效應力并不是一個科學的概念，其數值大于0，介質也不一定產生結構變形；其數值小于0，介質也可能產生結構變形。

7.2 新本體有效應力

毛博士在定義新本體有效應力(毛氏本體有效應力)時說[18]：“顆粒受到孔隙流壓和顆粒間應力的共同作用。為方便計算，將顆粒間應力分為兩部分來計算：一部分用來平衡孔隙流壓p，與孔隙流壓共同作用均勻壓縮顆粒，只引起顆粒體積變形，不引起顆粒形狀變形；另外一部分為超出平衡孔隙流壓之外的顆粒間應力σc-p，這部分作用力集中作用在顆粒間接觸面積上，不但引起顆粒體積變形，還引起顆粒形狀變形。”在這樣一個思路下，毛博士給出的新本體有效應力為[18]

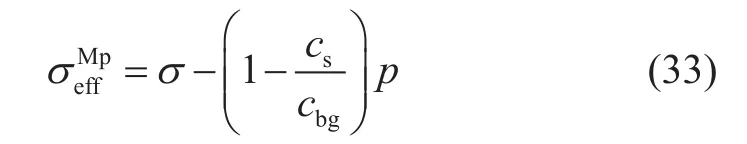
cbg的計算公式為

式中，cbsc為顆粒形狀變形導致的介質整體壓縮系數，MPa-1。

不知道毛博士是如何區分顆粒均勻壓縮產生的介質變形和顆粒變形產生的介質變形的？又是如何測量顆粒均勻壓縮的壓縮系數和顆粒變形導致的介質整體壓縮系數的？如果不能區分，又不能分別測量，毛氏本體有效應力還能計算和使用嗎？

7.3 總有效應力

在新雙重有效應力的基礎上，毛博士又定義了介質的總有效應力，即[18]

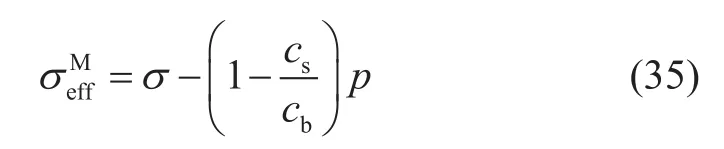
實際上，毛氏總有效應力就是式(30)的Skempton有效應力，只不過Skempton有效應力沒有明確說明決定介質的何種變形，而毛氏總有效應力明確說明了決定介質的結構變形和本體變形，即決定介質的總變形。

前面已經說過，Skempton有效應力就是Biot有效應力的一個特例，而且包含在Biot有效應力之中。Biot有效應力的Biot系數取經驗值，雖然不嚴謹，但方便實用。而Skempton有效應力則因為難以測量骨架壓縮系數和介質壓縮系數而不具有實用性。

更為嚴重的問題是，有了總有效應力之后，新雙重有效應力就沒用了，用一個總有效應力就可以解決多孔介質的力學問題了。毛博士的總有效應力就是Skempton有效應力，而Skempton有效應力又是一個不具有實用性的有效應力。這樣一來，所有的研究就又回到了原點。

8 新雙重有效應力的驗證

毛博士為了驗證新雙重有效應力的科學性，選擇了一些實驗結果，而不是生產現象。

(1)1955年Laughton的經典鉛粒高壓實驗[18]

實驗結果見表1。前面已經說過，Laughton實驗的最大問題是Biot系數出現了大于1的情況，多孔介質將會出現自行膨脹的現象。毛博士說[18]：“沒有顆粒形狀變形機理，則無法解釋孔隙度被壓縮到接近于0的實驗過程，用舊雙重有效應力理論也無法解釋有效應力系數在孔隙度為0時依然接近1的測試結果。”

“孔隙度為0，Biot系數為1”，這不是自我否定嗎？孔隙度為0的多孔介質，就變成了普通固體，也就不需要有效應力了，直接采用外應力研究介質的力學行為即可。如果再從外應力中減去孔隙壓力，即采用Terzaghi有效應力，這樣就把外應力的作用減弱了，固體力學從來沒有這么做過，毛博士這樣做過嗎？

(2)Hall圖版

巖石的孔隙壓縮系數定義為單位壓力的孔隙體積變化率[19]，即

式中，cp為巖石孔隙壓縮系數，MPa-1。

人們根據式(36)，采用體積法測量了巖石的孔隙壓縮系數[8]。H.N.Hall通過大量的實驗測量數據，統計并繪制出了壓縮系數與孔隙度的相關曲線，后人稱之為Hall圖版(圖18)[39]。Hall圖版長期應用于石油工程計算中，但是，Hall圖版有3個明顯的錯誤。第一，Hall圖版曲線顯示了錯誤的邏輯關系。根據Hall圖版，巖石越疏松或孔隙度越大，巖石的壓縮系數就越小，即巖石越難以壓縮。實際上，孔隙度越大或巖石越疏松，巖石應該越容易壓縮，巖石的壓縮系數應該越大。第二，Hall圖版與巖石的力學性質無關。根據Hall圖版，只要孔隙度的數值相等，不管巖石軟硬，其壓縮系數都相等。第三，用Hall圖版確定的巖石壓縮系數普遍偏高，高于了液態油和地層水，極端情況下甚至與氣體的壓縮系數相同，缺乏基本的合理性。由此可見，Hall圖版是一個錯誤的關系曲線。

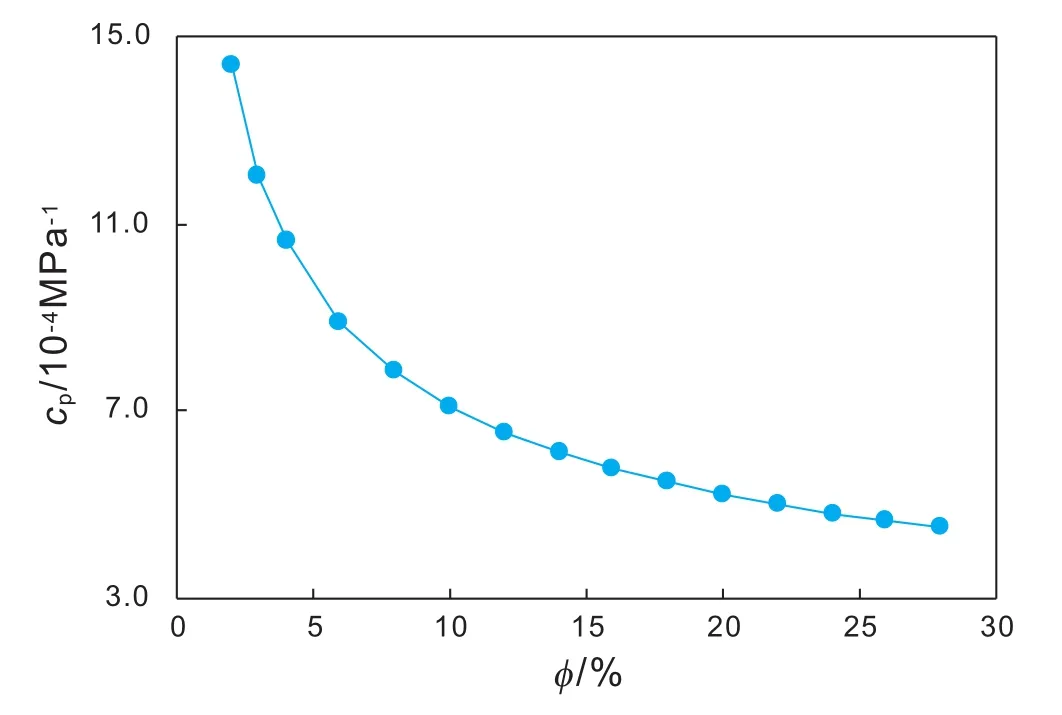
圖18 Hall圖版曲線Fig. 18 Hall's correlation plot

在雙重有效應力理論指導下，筆者導出了巖石孔隙壓縮系數的理論公式[7]，即

式(37)為巖石孔隙壓縮系數與孔隙度和骨架壓縮系數的關系方程，由該方程可以看出，巖石的孔隙度越大，巖石的孔隙壓縮系數也就越大，即巖石越疏松越容易壓縮。圖19顯示了巖石的孔隙壓縮系數與孔隙度的關系曲線(彈性模量為1×104MPa)。式(37)不僅呈現出了正確的邏輯關系，而且巖石的壓縮系數也遠低于了流體。

毛博士不僅不認同筆者提出的式(37)，還堅持認為實驗結果(Hall圖版)是正確的，并在新雙重有效應力理論的指導下，導出了一個新的巖石孔隙壓縮系數公式，即[18]

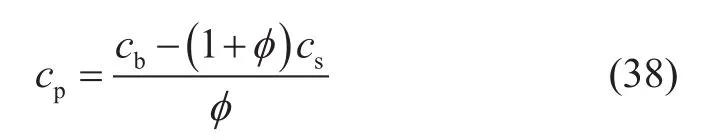
毛博士說[18]：“孔隙壓縮系數理論計算式(38)所反應的規律與Hall曲線圖版的規律也一致，Hall圖版如圖18所示，孔隙壓縮系數與孔隙度負相關，這是因為孔隙體積自身也是孔隙壓縮系數的分母。”

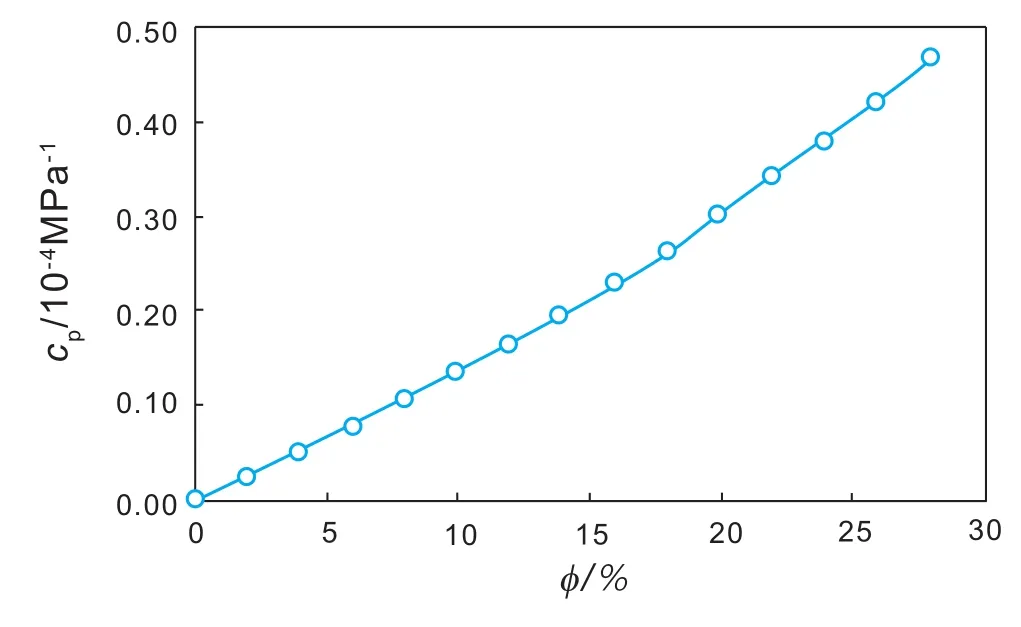
圖19 巖石孔隙壓縮系數曲線(彈性模量：1×104 MPa)Fig. 19 Rock's pore compressibility curve of soft minerals(elastic modulus: 1×104 MPa)

毛博士認為孔隙壓縮系數與孔隙度負相關，是因為孔隙體積在壓縮系數定義式(36)的分母上，孔隙度小，孔隙體積就小，因此，壓縮系數就高。這個邏輯關系顯然是不成立的。壓縮系數并非與孔隙體積成反比，而是與孔隙體積的變化率成正比，孔隙體積小，單位壓力的孔隙體積變化量就小，二者的比值并不一定高。如果毛博士的說法正確，則用1 mL水測量的壓縮系數一定比用1 L水測量的壓縮系數高。實際情況當然不是這樣，因為壓縮系數表征的是體積的變化率，與體積的大小無關，只與物質的性質有關。

其實，用體積法測量的巖石孔隙壓縮系數偏高，是巖心的表皮效應所致[40]，并不是巖石本身的性質。測量巖石壓縮系數時，把巖心放入塑料封套中，由于巖心與封套之間存在微間隙(圖20)，增加外壓時，巖心還沒有被壓縮，微間隙率先被壓縮了，由于微間隙中為空氣，因此才測量出了比油水還高的壓縮系數，有時候甚至與氣體的壓縮系數相同，巖石本身不可能有這么高的壓縮系數。

毛博士把實測的高壓縮系數歸因于“巖石顆粒間的滑動變形”[18]，其實，這個觀點是不成立的，致密巖石的顆粒之間都被膠結物膠結好了，壓縮實驗中不可能出現顆粒間的滑動現象(結構變形)。如果出現了顆粒間的滑動，巖心就碎了。實際上測量完壓縮系數之后，巖心仍然完好無損，說明沒有出現結構變形。結構變形只存在于疏松的介質之中(圖5)，致密介質不會出現。顆粒出現滑動，就不叫壓縮了，而叫壓實。由于無法取到完整的巖心，疏松介質的壓縮系數也是不能實測的，人們平時測量的壓縮系數都是致密巖石的。

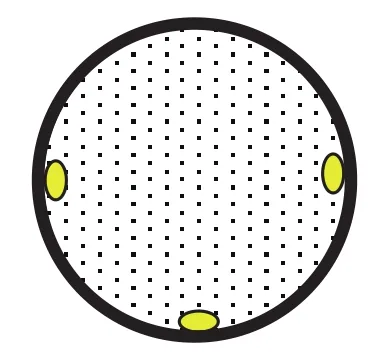
圖20 巖心—封套—微間隙Fig. 20 Core-sleeve-microinterstice

現在再分析一下式(38)，毛博士從公式形式上得出孔隙壓縮系數與孔隙度負相關的認識，這個認識明顯不正確。實際上，毛博士誤解了自己導出的式(38)，公式中介質外觀體積的壓縮系數并不是一個常數，而是隨孔隙度發生變化，孔隙度越大，巖石中的孔隙體積就越多，巖石就越容易壓縮，外觀體積的壓縮系數也就越高，筆者在文獻[9]中給出了外觀體積壓縮系數與孔隙度的關系式，即

把式(39)代入式(38)，整理后得到的公式正是筆者提出的式(37)，孔隙壓縮系數與孔隙度沒有出現負相關，而是正相關。毛博士沒有把公式推導徹底，在中間階段就下結論，于是就出現了上面的錯誤認識。錯誤產生的根源就是把外觀體積的壓縮系數當作常數了，雖然骨架的壓縮系數為常數，但外觀體積的壓縮系數卻是隨孔隙度變化的一個變量。

體積法之所以測量出了邏輯反轉的實驗結果(Hall圖版)，是由于測量方法本身存在的系統誤差所致。若采用筆者提出的彈性模量法[8]，則測量出了正確的邏輯關系，孔隙度越高的巖石，其孔隙壓縮系數也越高(表2)。而且，巖石的孔隙壓縮系數都遠低于了流體的壓縮系數。地層水的壓縮系數一般在(3～5)×10-4MPa-1。

9 結論

(1)Terzaghi有效應力為外壓與內壓的簡單差值，它只適用于極其疏松的多孔介質，不適用于致密介質。Biot有效應力是對Terzaghi有效應力的修正，由于Biot系數沒有明確的物理意義，通常取經驗值，因而是一個經驗公式。

表2 巖石力學參數和孔隙壓縮系數Table 2 Mechanical parameters of rocks and pore compressibility

(2)多孔介質存在本體變形和結構變形兩種基本的變形機制。與兩種變形機制相對應，多孔介質存在本體有效應力和結構有效應力兩個有效應力，合稱為雙重有效應力。雙重有效應力考慮了介質的物質結構，引入了介質的物性參數，可用于不同的介質類型，方便而靈活。

(3)新雙重有效應力的概念定義不嚴謹，總有效應力又替代了新雙重有效應力，而總有效應力又是Skempton有效應力，這讓新雙重有效應力失去了意義。

(4)新雙重有效應力無法解釋自然現象，也無法通過實踐的檢驗，在新雙重有效應力理論指導下導出的孔隙壓縮系數與孔隙度不是負相關，而是正相關。

【結束語】

Terzaghi有效應力為多孔介質的外壓與內壓的簡單差值，公式形式簡單，沒有待定參數，使用方便，因而受到人們的喜歡。但嚴格說來，Terzaghi有效應力并不科學，也沒有適用對象，只能近似用于極其疏松的土介質，并不適合于致密的巖石。Biot有效應力是對Terzaghi有效應力的修正，算是一個進步，但公式中多了一個待定參數Biot系數，使用起來相對麻煩一些。由于Biot系數缺少嚴格的物理意義，為了確定它的數值，人們做了大量的實驗研究。由于實驗存在的表皮效應和隨機誤差，測量的結果五花八門，且數量極大，但依然無法從中得出統一的結論。筆者從多孔介質的變形機制出發，通過嚴格的力學分析，建立了多孔介質的雙重有效應力，明確了有效應力的物理意義，給多孔介質的力學研究提供了方便，也讓實驗研究有了理論依據。希望雙重有效應力能夠成為大家研究多孔介質力學的理論工具，也歡迎大家繼續對其進行質疑和批判，以便今后對其不斷改進和完善。