基于多假設解分離算法的BDS/SINS緊組合完好性監視

王海東1,孫淑光,匡 杉

(1.大連國際機場，遼寧 大連 116033; 2.中國民航大學 電子信息與自動化學院，天津 300300)

0 引言

民航PBN運行要求衛星導航接收機必須具備接收機自主完好性監測(receiver autonomous integrity monitoring，RAIM)功能。RAIM算法利用冗余衛星信息進行完好性監視，在存在一顆衛星故障的情況下，要求接收機接收到的衛星(高度角5°以上)數量至少5顆及以上才能進行故障衛星的檢測，而要進行故障衛星的隔離則至少需要不少于6顆可見星。當飛機在更高精度要求的環境下運行時(如精密進近階段等)，為確保導航精度，部分測距誤差較大的衛星也可能被認為是故障衛星而進行隔離，這就會出現多故障衛星同時并存的情況，這種情況下，要進行故障的檢測與隔離，必然需要更多的可見星信息。SINS作為飛機的重要導航系統，與衛星導航系統進行緊組合導航計算，BDS已經在2018年12月26日完成了基礎性全球衛星的布網，在95%時間運行情況下，水平準確率達到10 m，因此BDS/SINS的組合，不僅可以增加系統的冗余信息，而且由于利用SINS高度和地球半徑信息，將地球作為緊組合算法中的一顆偽衛星，可以有效改善組合導航的幾何精度因子(geometric dilution precision,GDOP)，提高定位精度。

BDS/SINS組合導航可以實現二者的優勢互補，更好地滿足導航精度和帶寬等方面的要求。BDS觀測量對SINS的誤差漂移有一定抑制作用，而SINS可以改善BDS導航的連續性和完好性。民航飛機上通常有三套SINS，可以利用三個SINS信息對SINS進行組合前的設備故障預檢測，如果有設備故障，則首先將故障設備隔離，然后利用正常設備的位置信息進行組合導航的計算，如果設備沒有故障，則可以利用三套SINS設備輸出的加權平均值進行組合導航的計算，確保組合導航的精度。考慮到對機載三套SINS的適航要求，在BDS/SINS緊組合導航計算中，可以忽略SINS故障的情況，而僅進行故障衛星的檢測與隔離。

1 BDS/SINS緊組合方式

誤差的存在會降低系統的導航精度，從而影響到導航的完好性。BDS接收機的誤差主要有隨機誤差、非隨機誤差和外來誤差三類。各種誤差來源和性質明顯不同，其中隨機誤差主要和傳輸以及接收機自身性能有關；非隨機誤差主要有傳輸延遲、多徑誤差、鐘漂等，此類誤差會影響偽距測量精度。可基于誤差模型來修正前兩種延遲。而鐘漂誤差則可通過定位解算來確定；外來誤差主要和系統異常有關[2]。

SINS的誤差主要包括慣性測量單元(inertial measurement unit，IMU)傳感器誤差、初始對準誤差、計算誤差以及各種干擾引起的誤差等[3]。傳感器誤差主要包括陀螺和加速度計的常值誤差、漂移和標度因數等導致的誤差。具體分析可知，其中初始對準誤差主要包括初始對準的位置、速度和姿態誤差，組合導航中，主要受KALMAN濾波器的影響。計算誤差主要包括SINS計算的量化誤差、累積誤差以及參數設置誤差。干擾誤差主要是飛機受到沖擊或震動時的誤差。

1.1 BDS/SINS組合導航系統誤差分類

雖然BDS/SINS組合導航系統的誤差種類眾多，但根據其特性，基本上可以分為6類[3-5]：

1.1.1 階躍誤差

f(t)=Au(t-t0)

(1)

其中:A為誤差幅值；u(t)為單位階躍函數；t0為起始時間。這種誤差較大時，易用“快照”式的完好性監視算法檢測到[24]。部分導航偏差可以認為是長時間的階躍誤差，通常在導航解算中考慮消除。

1.1.2 斜坡誤差

斜坡誤差為一類隨時間逐漸變化的誤差，其誤差模型為：

f(t)=R(t-t0)u(t-t0)

(2)

其中:R為誤差斜率；u(t)為單位階躍函數；t0為誤差初始時間。由于誤差是逐漸變化的，斜率較小時(即慢變誤差)較難檢測。若采用“快照”式RAIM算法，只有當誤差累積到一定程度時，才可能檢測出[4]，設備老化可能產生此類故障。

1.1.3 隨機噪聲

隨機噪聲誤差較多，從電離層閃爍和對流層變化到SINS解算的各個過程都存在[24]。其誤差模型為：

f(t)=Aku(t-t0),

(3)

其中:N(m，V)為高斯正態分布，m為均值，V為協方差；η為誤差均值；u(t)為單位階躍函數；t0為起始時間。

1.1.4 隨機游走

隨機游走誤差主要存在于SINS傳感器，各種類型的陀螺和加速度計中，其誤差模型為：

(4)

其中:a(t)為高斯分布隨機變量；u(t)為單位階躍函數；t0為起始時間。

1.1.5 振蕩誤差

振蕩誤差為SINS的誤差類型，主要和SINS的慣導解算與誤差校正存在相關性[24]。可通過如下模型描述此誤差：

f(t)=Asin(t-θ)u(t-t0)

(5)

其中:A為故障幅值；θ為相位；u(t)與t0含義同上[24,28]。

1.2 運用卡爾曼濾波的BDS/SINS緊組合

BDS/SINS緊組合方式下，相應的輸入信息為BDS偽距域觀測量，并綜合相應的SINS輸出信息，而實現組合導航的目的[6]，如圖1所示。

BDS/INS緊組合將BDS接收機導航計算和BDS/SINS組合導航算法合二為一，輸入參數包括偽距、偽距率，組合系統解算時應用到卡爾曼濾波器。使用擴展卡爾曼濾波器，將BDS接收機觀測得的偽距、偽距率與飛機位置、速度之間的關系方程線性化[2]。

1.2.1 系統狀態方程

緊組合方式中，卡爾曼濾波器的系統狀態方程包括SINS和BDS的誤差方程。

在地球坐標系下建立SINS的誤差狀態方程。狀態向量包含位置誤差、速度誤差、姿態角誤差以及加速度計和陀螺的誤差，陀螺和加速度計誤差只考慮常值漂移誤差。

X(t)=[δrx,δry,δrz,δvx,δvy,δvz,δφx,δφy,

δφz,bgx,bgy,bgz,bax,bay,baz]T

其中:下標x、y、z代表在地球坐標系的三個軸向；δrx，δry，δrz為位置誤差；δvx，δvy，δvz為速度誤差；δφx，δφy，δφz為姿態角、航向角誤差；bgx，bgy，bgz為陀螺常值漂移；bax，bay，baz為加速度計常值漂移；wgx，wgy，wgz為載體坐標系下陀螺的噪聲；wax，way，waz為載體坐標系下加速度計的噪聲[6-8]。

(6)

由SINS的解算方程可得系統的狀態轉移矩陣為：

WB(t)=[wgxwgywgzwaxwaywax]T

美國國立衛生研究院建立了分工明確、責任可查、合作協調的管理制度，保障基金資助管理水平。一是分階段管理，美國國立衛生研究院科學評審中心主要負責申請的受理與分配、大部分競爭性項目的初評工作，美國國立衛生研究院各研究所負責二審及項目立項和過程管理。二是管理隊伍分工明確，團隊協作。美國國立衛生研究院各研究所項目管理人員負責日常管理、審核申請是否符合規章制度和指南；項目官員負責指南編制、審核項目進展報告、現場檢查等；項目管理人員、項目官員及財務、臨床實驗專業管理人員組成科研管理團隊，相互配合，充分發揮專業化管理的優勢和效率。

BDS接收機設置的狀態向量為和接收機時鐘對應的誤差，主要包括等效距離變化率誤差和等效距離誤差(分別表示為δtru，δtu)，在分析時前者可看作為一階馬爾科夫過程。可通過如下方程描述這兩個誤差：

(7)

其中:βtru為相關時間，wtu，wtru為白噪聲[9-10]。

因此，BDS接收機誤差的狀態方程為：

(8)

式中,

式(6)、(8)合并即可得BDS/INS緊組合卡爾曼濾波的系統狀態方程：

(9)

即：

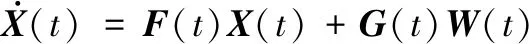
(10)

X(t)=[δrx,δry,δrz,δvx,δvy,δvz,δφx,δφy,δφz,bgx,

bgy,bgz,bax,bay,baz,δtu,δtru]T

1.2.2 系統量測方程

(11)

將上式在(x，y，z)處泰勒展開，舍棄高階項，得：

(12)

式中,

第i顆衛星與用戶的慣導位置之間的距離為：

ρIi=ri+ei1δx+ei2δy+ei3δz

(13)

BDS接收機觀測得的接收機到第i顆衛星的偽距為ρBi=ri-δtu-υρ。其中，δtu為等效距離誤差，vρ為量測噪聲，其主要和偽距殘差有關，常見的如多徑誤差等[2]。

可通過如下表達式描述距離差量測方程：

(14)

綜合式 (6)～(14)，可以得到最終的偽距量測方程：

Zρ(t)=Hρ(t)X(t)+Vρ(t)

(15)

其中:

(16)

SINS位置與第i顆衛星之間的距離變化率在(x，y，z)點線性化之后得到：

(17)

(18)

由于SINS輸出的導航參數是真實值與誤差值之和，所以有：

(19)

由此，SINS導航解算的距離變化率可表示為：

(20)

BDS接收機測量輸出的偽距率為：

(21)

綜合式(20)和(21)，緊組合導航系統偽距率量測方程如下：

(22)

由此，偽距率量測方程可表示為：

(23)

其中:

由以上各式得到偽距、偽距率組合方式測量方程為[18]：

(24)

2 多假設解分離的完好性監視

完好性主要表示系統在無法完成預定工作情況下及時準確的發送有效告警的能力[5,11-13]，對這種系統而言，需要在規定期限內提供超限警報信息給用戶[5,11-14]。可通過三個指標描述完好性，也就是完好性風險，保護限、告警時間，以下進行具體描述[5,11-15]。

保護限(protection limit，PL)可劃分為水平(horizontal protection limit，HPL)和垂直(vertical protection limit，VPL)兩個方向的保護限，可通過其反映出相應虛警和漏檢概率的徑向位置誤差最小值[11,12,15]。后續以水平保護限為例分析多解分離的完好性監視方法。根據PBN運行要求及特點，不同的飛行階段對應不同的告警限值(alarm limit，AL)。當PL超出指定飛行階段的AL時，系統應給出告警。

告警時間(time to alarm，TTA)具體表示從系統出現故障到發出告警的時間差，告警時間為Δt=t2-t1。根據安全性要求，不同飛行階段所對應得最大允許告警時間tmax不同，若Δt≤tmax表示系統完好性能及時告警；反之，為漏警。

完好性風險含義為系統誤差超過告警限制但沒有發出報警的概率[4,11]。若計算結果表明相應位置誤差超過設定值情況下，需要在告警期限內發出報警信息；而若沒有發出報警，則可判斷存此類風險。也即：

PIntegrity_Risk=

(25)

2.1 基于多解分離的擴展卡爾曼濾波結構

如圖2反映出這種濾波器結構，分析可知其中具體包括主濾波器F00、N個子濾波器和N-1個次濾波器。而對應的主濾波器的量測信息主要為全部N顆BDS可見星的測量結果；其中子濾波器中含有其他BDS可見星的測量信息；次濾波器中的觀察信息和前者的屬性相同。在運行過程中接收到的衛星信息中有故障情況下，必然有一個子濾波器的狀態解和主濾波器的存在偏離。這樣在主濾波器和一個或者多個子濾波器的分離解大于設定值情況下，系統會發出報警信息，可根據相應的子與次濾波器的分離解來實現隔離目的[3,13,19]。

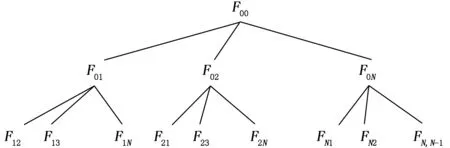
圖2 多解分離濾波器結構

2.2 基于多解分離的完好性監視

可通過如下表達式描述k時刻主濾波器和某子濾波器估計解的分離向量：

(26)

其協方差為：

(27)

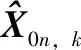
建立起各子濾波器統計量：

(28)

在已知誤警率PFA條件下，可確定出和各統計量d0n相關的判斷閾值T0n為：

(29)

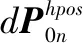
在隔離BDS觀測數據過程中，可應用N個子濾波器相關的統計量，相應的判據表示為：

1)無故障H0：所有子濾波器對應的檢驗統計量均有d0n≤T0n；

2)有故障H1：至少存在一個子濾波器對應的檢驗統計量d0n>T0n[3,13,19]。

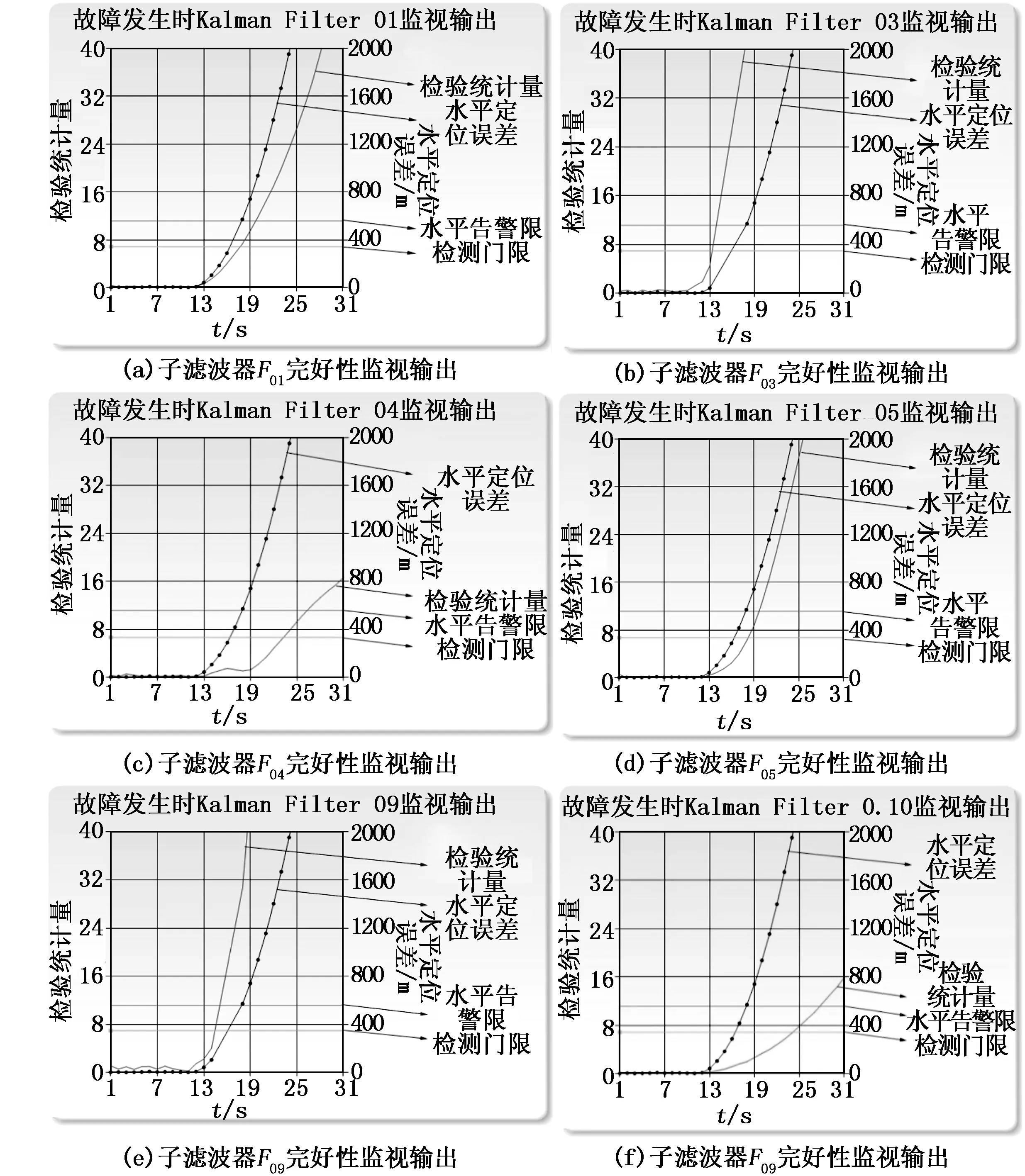
圖4 故障發生時各子濾波器的完好性監視輸出

對其中子和次級濾波器的分離解進行分析就可塑實現故障隔離的目的。相應的算法和故障檢測的基本上一致。可基于其解分離向量確定出統計量dnm和對應的閾值Tnm。檢測并驗證第r顆衛星故障的判據為：對全部n≠r，有一個或者多個次濾波器相關的統計量高于閾值[3,13,19]。

每個子濾波器的水平保護限用下式計算：

HPLn=T0n+a0n

(30)

其中:T0n表示該子濾波器對應的判決門限；a0n表示該子濾波器F0n本身的水平位置誤差門限[11,23,41,50]。記λP0n為水平位置誤差向量協方差陣P0n的最大特征值[3,11,13,19]，根據漏檢率PMD要求，可得：

(31)

進而得到多解分離的水平保護限為[11,,23,41,50]：

HPL=max(HPLn)=max(T0n+a0n)

(32)

2.3 BDS/SINS緊組合完好性監視仿真與分析

在以上分析基礎上，接著模擬仿真這種接收機的衛星觀測數據誤差情況。在進行導航解算過程中，可在各時空點選取滿足要求的GDOP值最大的6顆可見星，且將故障信息加在檢測難度最大的衛星上。

故障參數設置如下：對應的觀測衛星GEO3在11 s時出現斜坡率為0.63 m/s的斜坡故障，持續時間為129 s。飛行階段設定為非精密進近階段，漏警、誤警概率要求、告警時限遵循非精密進近階段的要求，如圖3所示。

圖3 測試階段多解分離算法計算的保護限

在出現故障情況下，如圖4(a，b，c，d，e，f)顯示了各卡爾曼濾波器的輸出結果，分析此圖可知11 s時在GEO3的觀測值出現了0.63 m/s的斜坡誤差，運行過程中，子濾波器F03在13 s時檢驗到觀測值超出設定值，而發出報警提示。在18 s時各子濾波器位置解的水平定位誤差高出設定值，據此可判斷出：在出現衛星故障情況下，多解分離法可控制定位誤差低于設定值，或者發送報警提示，而相應的告警時間也在合理限度內，滿足要求。

為了對這種算法的虛警率和漏檢率進行驗證，判斷是否在許可范圍內，而開展了蒙特卡洛試驗。在此實驗過程中選取8 000個時空點來模擬仿真，相應的故障設置情況為，每隔120個時空點隨機情況下加一次故障，對所得結果進行整理，如圖5所示，測試數據的仿真情況見表1。

表1 statistical result data of Monte Carlo simulation

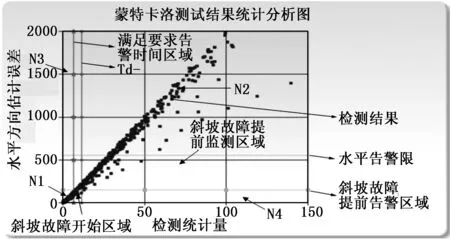
圖5 蒙特卡羅測試結果統計分析圖

分析以上結果可知，虛警率為1.25×10-4，而漏檢率為0，虛警率高的原因為多解分離算法結果容易受到慢變的斜坡故影響。

3 結束語

本文分析了SINS和BDS導航的誤差特點，搭建了擴展卡爾曼濾波的BDS/SINS深組合系統，利用多假設解分離算法對BDS/SINS緊組合導航系統的完好性監視算法進行了完善，選擇最大GDOP的6顆衛星組合，通過在最難檢測的衛星上人為加入誤差信號，進行故障衛星的檢測與隔離，并計算水平保護限，仿真結果表明該方法能夠有效實現故障衛星的檢測與隔離，滿足導航系統完好性算法的要求。論文選擇了最差的情況，只考慮單顆衛星故障。當多顆衛星故障時，可以用同樣的方法解決，但所需的卡爾曼濾波器的數量會急劇增加，影響處理速度。