以“問題”為主導,打造有效的中職數學課堂
張玲莉
摘要:“問題驅動”教學法,要求教師精心設置問題:創設問題激發學生學習數學的興趣和欲望、確定問題引導學生主動觀察思考分析、提煉問題引導學生主動合作交流探討、延伸問題引導學生主動嘗試歸納總結,筆者以“問題串”形式,闡述如何打造一個有效的中職數學課堂。
關鍵詞:中職;數學課堂;問題
中圖分類號:G633.6文獻標識碼:A文章編號:1992-7711(2020)04-0173
隨著中職課程的不斷深化改革,要求教師在教學過程中要更加關注學生的學習經歷、學習經驗的獲得以及學習方式的轉變。在這種課程理念指導下,筆者通過自己不斷的教學實踐得出:“問題驅動”教學法,能創建一個有效的中職數學課堂。筆者以《正弦函數的圖像和性質》為例,談談如何以“問題”為主導,打造出一個有效的中職數學課堂。
這節課選自《數學》基礎模塊(上冊),其主要內容是正弦函數的圖像與性質。本節內容共分兩個課時,本課為第一課時,主要利用描點法畫出函數y=sinx,x?[0,2π]的圖像,通過觀察圖像的特點,介紹“五點作圖法”,再通過圖像感知正弦函數的主要特征。教學對象為中職高一學生。
如何通過巧妙地設計教學思路,將要講授的知識以“問題串”方式蘊含于任務之中,使學生在回答或解決問題中完成任務,達到掌握所學知識的目的。下面,筆者將具體闡述。
一、創設問題激發學生學習數學的興趣和欲望
建構主義理論指出學生不是空著腦袋走進教室的,在以往的生活、學習和交往活動中,他們逐步形成了自己對各種現象的理解和看法,而且他們具備利用原有知識經驗進行推論的智力潛能。因此,情境問題的設計要接近學生現有的認知結構。
問題1:觀察下列函數圖像,你能說出它們分別是什么函數嗎?
設計意圖:讓學生從熟悉的一次函數、二次函數入手,讓學生感悟函數與圖像之間的一一對應的關系,為本課作正弦函數的圖像埋下伏筆。
問題2:觀看視頻:《彈簧振子的圖象》,猜想:這個圖象可能會對應哪個函數嗎?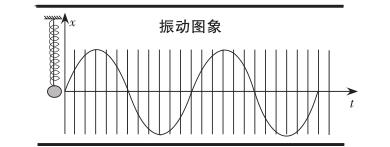
設計意圖:教師用多媒體呈現教學內容,學生觀看多媒體課件展示的動畫。這樣引出課題的過程既讓學生感知正弦函數與生活息息相關,同時也激發了學生學習的興趣。讓學生體會數學來源于生活又服務于生活。
二、確定問題引導學生主動觀察思考分析
學習不僅僅是知識由外到內的轉移和傳遞,而是學習者主動地建構自己知識經驗的過程,因此我們要留給學生一定的時間去自主探索。在提出問題4后我們留給學生5分鐘時間。根據學生完成情況的不同可以相應調整時間。
問題3:正弦函數的定義是什么?
學生快速地回答:形如y=sinx,(x?R)叫做正弦函數,用x表示角的弧度數(自變量),y表示因變量。
設計意圖:由此及彼,開門見山,不拖泥帶水地復習正弦函數的概念。為如何作圖打下伏筆,實現遷移知識的目的。
問題4:如何作正弦函數y=sinx,x?[0,2π]的圖像?
引導問題(1):在初中,我們是如何畫一次函數、二次函數的圖像?步驟?
復習描點法步驟:列表;描點;連線
◆用代數描點法畫正弦函數y=sinx,x?[0,2π]的圖像
先讓學生填360度角平分12份對應的正弦值的表格,然后把角度換成對應的弧度,接著描點,再連線得到下圖。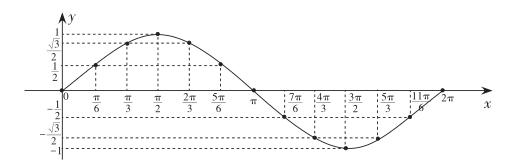
設計意圖:由于平時接觸角的角度制比較多而對弧度制不是很熟,先用角度制過渡,由已知到未知,由簡單到復雜,降低難度并體驗事物之間的相互轉化。加強熟悉作圖的一般步驟:列表、描點、連線,學會用新知識作y=sinx,x?[0,2π]的圖像。
引導問題(2):觀察正弦函數y=sinx,x?[0,2π]圖像中起著關鍵作用的點是哪些點?
【設計意圖:提出問題,培養學生認真觀察和勇于探索、勤于思考的精神。提高學生的觀察能力及語言表達能力。再一次熟悉作圖的一般步驟:列表、描點、連線。并得出五點作圖法這一概念。】
三、提煉問題引導學生主動合作交流探討
教師在教學過程中要組織學生把自己的見解表達出來,并傾聽和評價他人的見解。在自主探索的過程中,教師通過巡視的方法,了解學生的不同見解以及對問題理解的不足之處。自主探索之后,教師將學生對問題的不同見解及不足之處通過板演或敘述的方法呈現出來,供學生交流。分析出問題的本質,并選擇最適合自己的解決問題的方案。
問題5:你會利用“五點作圖法”作函數y=sinx,x?[0,2π]及函數y=1+sinx,x?[0,2π]的簡圖嗎?
教師示范第一個函數的作圖過程,培養學生的模仿學習能力及動手作圖能力。教師在講解的時候要和學生說縱坐標取點時要掌握訣竅:先定好2π,再取中間π,……,這樣就會比較精確。
設計意圖:讓學生小組合作,在導學案上自己也做一遍教師板書的圖像,再完成變式練習,教師巡視尋找各種糾錯的學生作圖結果,并通過手機傳回到大屏幕上展示講解。學生從研究方法的拓展中得到新的知識點,發揮學生的主觀能動性,培養學生觀察發現、合作交流的能力。
問題6:觀察兩個圖形,它們之間有什么關系?
【設計意圖:這個設計看似僅僅討論著兩個函數圖像之間的關系,實際上還隱藏著一個目的,通過類比,從上下平移過渡到左右平移,從而得出正弦函數在R上的圖像。】
問題7:如何作y=sinx,x?R的圖像?
引導學生通過問題6,猜想由函數y=sinx,x?[0,2π]的圖像左右平移,得到y=sinx,x∈R的圖像。
設計意圖:學生觀察,小組交換想法得出結論。學生觀察并在前一題上下平移的暗示下,很容易想到左右平移,從而得到正弦曲線。培養學生不僅僅只用圖形粗略的驗證,數學驗證還需要嚴密,需要用代數的方法。讓學生體會從特殊到一般的研究方法。
反思本節課,在新課改的指導下,教師首先為學生搭建自主探究、討論、交流的平臺。其次是整個教學過程以問題為載體,緊緊圍繞著正弦函數的圖像引導學生分析、探究、歸納、概括。讓學生經歷了圖像形成的四個階段:感知認識階段、分析本質屬性階段、概括形成定義階段、應用與強化階段,有效地實現了學生對正弦函數的圖像的構建。
(作者單位:浙江省瑞安市農業技術學校325200)

