立足推理，親歷“再創造”的過程

程婭

【摘要】數學教學應當更多地關注學科本質，立足推理，讓兒童經歷知識再創造的過程。本文以《圓的面積》教學為例，對課堂教學進行重構和反思，讓兒童經歷數學研究的過程，經歷數學歷史發展的過程，經歷知識再創造的過程。

【關鍵詞】以面度面 推理 再創造

一、叩問：教什么，怎么教，有什么用

一個偶然的契機，筆者受命執教蘇教版數學五年級下冊《圓的面積》。這一課時安排了3個例題，容量大，難度高，既要有活動操作的體驗，又要邏輯推理的發展，是大家公認的“硬骨頭”。筆者開始思考：教材為什么這樣安排？這樣的安排跟學生的素養發展之間有怎樣的聯系？學生的起點在哪里？怎樣引導學生經歷知識的“再創造”？

二、慎思：“起點”和“終點”之間需要什么

1.教材的立意

（1）關于例7

幾個版本的數學教材都相繼取消了數方格，那數方格在這里的作用是什么？回顧長方形、平行四邊形的面積公式推導過程，都是要先數方格。那數方格的作用僅僅是比較、估算嗎？繼續回顧數方格是緣于面積的比較，面積單位的產生，就知道教材堅持數方格傳遞的思想：數方格是為了度量。面積是度量幾何學的重要組成部分，任意一個新圖形的面積，都可以“以面度面”。量出面積，再探究與相關量的關系，因此數方格是度量思想的體現。例7的作用是什么？筆者以為：是要讓兒童經歷合情推理的過程。要讓學生重新經歷人類對圓周率探索漫長過程中的關鍵性步子，就必須發掘例7在數學知識“再創造”過程中的重要作用：創設“區間精確”的路徑，親歷以面度面的測量驗證過程，也為猜測提供依據，合情推理也應是一種證據推理。

（2）關于例8

小學生以感性思維為主，動手實踐是探究新知的主要方式之一，安排幾個操作合適呢？“轉化為長方形、三角形、梯形”這個問題對學生來說有難度， 但它的價值在于能讓學生養成多角度思考的習慣， 能有意識地尋求不同的方法解決問題， 能綜合已學知識來思考新問題。鑒于一節課時間有限，教師可以將“轉化為長方形”作為本課的基礎研究，而“轉化為三角形、梯形”作為課后拓展研究。例8的作用是什么呢？除了動手操作，轉化前后的對接里還有思辨，有空間想象、幾何推理、視覺空間推理。例7合情推理有助于探索解決問題的思路，發現結論。而例8則是“把實際操作與幾何推理結合起來，發揮實際操作在幾何思維中的重要作用”。

（3）關于例9

例9不僅僅是一個簡單的公式代入練習，必須要考慮到：學生是首次計算關于一個數的平方與另一個數的積，會出現計算順序的差異。因此，計算時先算r2也是需要教師引導學生對比發現的地方。此外，學生嘗試用π×102=100π這樣的代數式表示運算的結果，也為后續代數的運算奠定基礎。

所以這3個例題都很重要，對學生思維的發展有深刻的影響。

2. 學生的起點

（1）學生有過多次用數方格來研究面積的經驗：研究長方形、正方形、平行四邊形及不規則圖形的面積。

（2）學生有用轉化法來探究面積的經驗：研究平行四邊形面積時，轉化成長方形;研究三角形面積、梯形面積等時都用到了轉化的方法。

（3）學生有較多數學研究的經驗：很多研究都是先大膽猜測，再實驗求證，最后推理驗證。例如圓的周長的探究，也是先猜測和什么有關，估計是什么樣的關系，實驗驗證關系。

3. 教學的著力點

（1）經歷知識的產生過程，體會極限、轉化的數學思想，增強空間觀念，發展數學思考。

（2）經歷數學研究的過程，經歷猜想、操作、驗證、討論和歸納等數學活動的過程。

（3）經歷數學歷史發展過程，感受面積測量發展的歷史，感受數學知識內在聯系的邏輯之美。

三、重構：聆聽兒童數學思考真實的聲音

（一）類比推理：把握認知起點，凸顯遷移價值

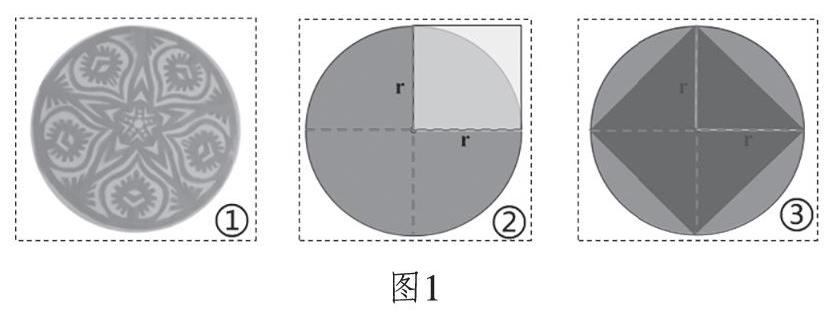
師：今天老師帶來了我們學校狀元娃的一些剪紙作品。剪這張剪紙圖案，至少需要多大的圓形紙片？（PPT出示圖1①）

師：求圓形紙片的大小，就是要求什么？（板書課題）

師：這個圓形紙片的面積指的是什么？

師：猜一猜，圓的面積與它的什么有關？（半徑、直徑、周長、π）

師：是這樣嗎？（PPT演示長短兩條半徑各旋轉一周畫出圓的過程）

師：圓面積的大小與半徑是什么關系呢？我們可以借助一個和半徑有關的圖形——正方形來研究。（PPT出示例7，隱去方格，如圖1②）

師：正方形和圓有什么關系？

生1：正方形的邊長就是圓的半徑。

生2：圓面積大約是正方形面積的4倍……比4倍少一些。

（師板書≤4r2）

生4：四個三角形合起來就是兩個正方形，圓面積比兩個正方形大一些。也就是說， 圓面積比2r2多一些（如圖1③）。

生5：圓的面積比4r2少一些，比2r2多一些。

（二）合情推理：立足舉例驗證，親歷以面度面

師：那圓的面積到底是r2的幾倍呢？讓我們來數一數。

生1：圓的面積是52cm2，正方形面積是16cm2，所以圓的面積大約是正方形面積的3倍多一些。

師：所有這樣的圓和正方形都有這種關系嗎？

生：不確定，還需要進一步舉例驗證。

（小組合作：數一數、算一算、填一填）

師：仔細觀察（指向表格），你有什么發現？

生2：圓的面積都是正方形面積的3倍多一些，也是半徑平方的3倍多一些。

（三）演繹推理：拓展認知邊界，感受極限思想

師：要想更準確地知道圓的面積，你有什么好辦法？

生：以前把平行四邊形面積剪拼為長方形面積;把三角形、梯形面積轉化為平行四邊形的面積。圓的面積是不是也可以轉化成一個學過的圖形呢？

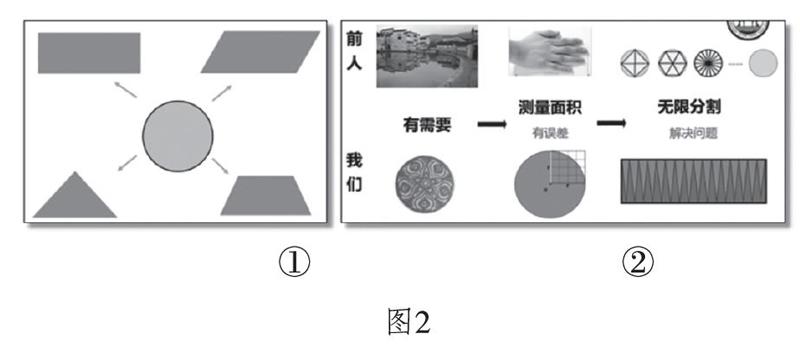
師：怎么轉化呢？轉化成學過的什么圖形呢？（出示圖2①）

師：借助材料袋里的材料，我們先把圓剪拼成一個平行四邊形看看有什么發現。

（展示交流：黑板有序展示學生成果）

師：仔細觀察，發現了什么？

生：拼成的圖形越來越接近平行四邊形。

師：繼續分下去呢？

生：平行四邊形斜邊會豎起來！

師：那就是？

生：長方形。

師：是的，就是這樣，我們把圓轉化成了長方形。

（師板書：轉化）

師：觀察轉化前后的圖形，思考：拼成的長方形和原來的圓有什么關系？

生（小結）：圓的面積可以用公式S=πr2 來計算。

（四）回顧反思：立足研究過程，勾連數學文化

師：看來圓的面積和圓的半徑確實有著密不可分的聯系。回顧今天的研究過程，我們是怎樣做的？

生：先猜測和什么有關，然后估計是怎樣的關系。通過不斷地觀察比較，逐步縮小范圍，再數方格進一步縮小范圍，最后通過轉化推導出完善的面積公式。

師（小結）：是的，其實我們做任何研究都需要這樣大膽猜想，實驗求證，推理驗證。讓我們來看看前人是如何研究圓的面積的吧。

播放微課視頻：（逐步出現圖2②）數學始于需要，早在幾千年前，我們的祖先由于田地、湖泊的測量需要，開始了對面積的探究。他們先是用手掌、腳印及同樣大小的小正方形比較面積的大小，后來，人們應用出入相補的原理，將圓的面積轉化為它內接十二邊形的面積，因此有了“周三徑一”的說法。隨著數學的發展，我國數學家劉徽指出有限次的分割、拼補是有局限的，進而想到無限分割，把圓的面積轉化為求無數個小三角形的面積。

師：前人怎樣用手掌、腳印比較面積啊？“周三徑一”是什么意思？劉徽為什么要無限分割呢？回顧我們今天的研究，是不是和前人有驚人的相似之處？

生：是的，我們也是有研究圓形紙片面積的需要，先估一估，然后想到用數方格來測量，不過這種方法有很大的誤差，最后想到通過無限分割把圓面積轉化成為長方形的面積，問題才得以解決。

師：現在要解決之前的這個問題，你需要什么條件？

師：剛才我們是把圓轉化成長方形來研究的，其實也可以把圓轉化成三角形、梯形。那三角形、梯形和圓又有什么聯系呢？讓我們帶著這個問題走進課后的研究。

四、追擊：讓兒童經歷再創造

教學不能只關注知識，還應關注情境背后的能力、知識背后的文化和精神、技巧背后的思想和方法、邏輯背后的直觀和猜想。因此在推理過程中還要關注兒童親歷怎樣的歷程。

（一）經歷圓面積知識產生的過程

主要通過一條主線（如圖3），這個過程是從區間到精確的過程。

（二）經歷數學研究的過程

引導學生經歷猜想、估計、操作、驗證、討論和歸納等數學活動的過程，感受數學研究的過程：大膽猜想→實驗求證→推理驗證。類比科學研究的過程，有一個共同點：有探究的需要→猜測（大膽提出一些假設）→實驗求證（用已掌握的測量方法測量幾個圓片的面積）→推理驗證（化曲為直和假設對接）→解決問題。

（三）經歷數學歷史發展過程

回顧面積發展歷史，人類對面積的研究是始于度量的需要，在沒有面積測量方法以前，只能借助一些現有的面積比較面積的大小。從“周三徑一”到準確地測量出圓的面積，前人想到了利用無限分割轉化成無數多個三角形的和。這節課的研究也是如此，始于解決問題的需要，借助有關圖形估一估，為了更精確，想到用小方格度量;為了消除誤差，進而想到剪拼轉化成長方形。