男男性行為人群中HIV/AIDS行為干預的動力學模型

梁小嬌,阮玉華, 婁 潔

(1.上海大學理學院,上海200444;2.傳染病預防控制國家重點實驗室,北京102200)

自1981年美國加州發現首例艾滋病男男性行為者(men who have sex with men,MSM)以來,這種HIV/AIDS風險一直存在.近年來,中國艾滋病病毒總體上處于低流行水平,但在男男性行為者(也稱男同)中呈現高流行態勢,并逐漸向一般人群擴散[1].盡管各種研究、醫療以及公共衛生組織等一直在努力,但全球艾滋病男同感染率和發病率卻很高.這種趨勢已引起各界重視,并采取多種干預措施.男同的多性伴、安全套使用率低、偶然性行為多等特征,使其成為HIV感染與傳播的重要人群[2].

2014年聯合國艾滋病規劃署報告稱:截至2013年底,全球現存活艾滋病病毒感染者和艾滋病病人共3 500多萬人.聯合國艾滋病規劃署提出了“2030年終結艾滋病”的愿景,并提出“3個90%”防治目標,即:90%的感染者通過檢測知道自己的感染狀況,90%已經診斷的感染者接受抗病毒治療,90%接受抗病毒治療的感染者病毒得到抑制.

艾滋病的預防可以分為三級:一級預防是預防末感染的人感染艾滋病病毒;二級預防是使感染者能夠早期診斷,早期得到治療、教育和咨詢服務,延緩艾滋病病毒在人群中的進一步傳播;三級預防是通過醫療和社會支持服務改善人的生命質量,延長他們的生存時間.

1 模型

在以往的艾滋病干預模式中,更多的是對已感染的患者進行干預[3-4].本模型主要探討:若能做到一級預防,相對于加大對感染者的干預力度,而是增加對艾滋病易感者的干預,如宣傳教育、增加安全套的發放等措施,那么是否能更好地降低艾滋病的感染率.基于上述設想建立動力學模型,其中S為易感者,I為感染者,T為治療期患者,A為HIV晚期患者.I與T之間的相互轉化是由于部分患者經檢查發現自己感染艾滋病,會選擇進行治療,但部分感染者可能在治療過程中出現排斥反應,放棄治療.帶有上標e的為接受這種額外行為干預的人群,下標1和2的分別表示急性感染期和慢性感染期的患者.HIV傳播示意圖如圖1所示,其中各倉室動力學方程如下:

式中,

圖1 HIV傳播示意圖Fig.1 Schematic diagram of HIV transmission

在模型(1)中,M為易感者的輸入量,bs為對易感者的宣傳教育的覆蓋率,b1,b2分別為對處在急性感染期和慢性感染期的HIV陽性者的行為干預率,ν為急性感染期到慢性感染期的進展率,ω為感染者從慢性感染期到發病期的進展率,k為從急性期治療階段到慢性期治療階段的進展率,σ為從慢性期治療階段到發病期的進展率.急性期分別為感染者在急性感染期和慢性感染期的治療率,α1,α2分別為感染者在急性感染期和慢性感染期的退出率,分別為被干預的感染者在急性感染期和慢性感染期的治療率,分別為被干預的感染者在急性感染期和慢性感染期的退出率,β1為急性感染期的傳染率,分別為慢性感染期、被干預的急性感染期、被干預的慢性感染期、急性期治療階段以及慢性期治療階段對急性感染期傳染率的比率,δ為發病者的死亡率,d為自然死亡率,η為一級預防干預下男男性行為者人群增加的有效安全套使用率.

2 數值模擬

本工作中目標人群為北京市男同,且已知2000—2010年的感染率[3],其中各參數的意義、取值及其范圍如表1所示.在不考慮對易感者進行宣傳教育的情況下(bs=0),假設一些參數取固定值,對于部分取值不確定的參數以及各類人口的初始值,通過馬爾可夫-蒙特卡洛(Markov Chain-Monte Carlo,MCMC)方法,根據馬爾可夫過程,首先從給定的初始值的狀態出發,模擬馬爾可夫過程,不斷進行狀態轉移,最終收斂到平穩分布.擬合出一條與已知感染率相匹配的最佳曲線,從而得到那些不確定參數及人口初始值的均值及方差.通過MCMC方法擬合出的參數取值情況(見表2),其中收斂性判斷值越接近于1,表示參數擬合效果越好.

文獻[11]顯示,2014年北京市男同HIV感染率為12.7%.由于缺少2011—2013年的感染率數據,本工作以2010年的感染率為基準,通過對2000—2010年的參數擬合得到(見表2).通過將均值±1.96倍標準差的方法,即參數取值范圍的95%置信區間,給予參數新的取值范圍.對于2010—2014年的治療率γ在范圍[0.75,1.00]內隨機抽取,擬合得到2010—2014年的感染率,結果如圖3所示.

2014年北京市男同HIV感染率為12.7%.由圖2可以看到,擬合的2014年的感染率范圍在[9.79%,19.52%],平均感染率為13.44%.考慮到隊列調查的局限性使得12.7%的感染率會比實際情況偏低,本工作得到的感染率的箱形圖符合實際情況,說明擬合出的參數具有合理性.

為了預測一級預防的效果,分3種情況模擬2014—2020年艾滋病感染率曲線,其中參數取值和2011—2014年范圍相同.一級預防的效應參數η在[0.50,0.75]內隨機抽樣,即安全套的有效使用率在[0.50,0.75]內隨機抽樣.每種情況都進行了10 000次拉丁超立方抽樣(Latin hypercube sampling,LHS).

表1 參數的意義及MCMC擬合時的取值范圍Table 1 Description and uncertainty range of parameters for MCMC fitting

表2 擬合參數取值情況Table 2 Values of fitted parameters

圖2 2010—2014年北京市艾滋病感染率擬合的箱形圖Fig.2 Box-plot of HIV infection rates during 2012—2014 in Beijing

情況1 bs=0,η=0,即沒有一級預防干預,對于HIV陽性者的治療率γ在[0.75,1.00]內隨機抽取,對HIV陽性者的行為干預率b1,b2保持原來的值不變.

情況2 bs=0,η=0,即沒有一級預防干預,對于陽性者的治療率γ在[0.75,1.00]內隨機抽取,提高HIV陽性者的行為干預率b1,b2為原來的3倍.

情況3 一級預防干預下,即對易感者的宣傳教育有效覆蓋率bs=0.25,安全套使用率η在[0.50,0.75]內隨機抽樣,對于陽性者的治療率γ在[0.75,1.00]內隨機抽取,而對處在感染期的HIV+的行為干預率b1,b2保持原來的低水平不變.

情況1和情況2的結果對比如圖3所示.可以看出到2020年,MSM人群中的感染率會有所下降,但效果不是很明顯.

再將情況1和情況3進行對比,即保持其他參數不變,增加對易感者的宣傳教育的有效覆蓋率(bs=0.25),結果如圖4所示.從圖中可以看出:到2020年,若不加入對易感者的宣傳教育的覆蓋率(情況1),則感染率為20.5%;增加對易感者的有效宣傳教育的覆蓋率(情況3),則感染率為14.91%.因此,加入對易感者的有效宣傳教育之后,感染率會有很明顯的降低.

圖3 北京MSM人群的HIV感染率在情況1與情況2下的對比Fig.3 Comparation of HIV infection rate between situation 1 and situation 2 in Beijing MSM population

圖4 北京MSM人群的HIV感染率在情況1與情況3下的對比Fig.4 Comparation of HIV infection rates between situation 1 and situation 3 in Beijing MSM population

表3為3種不同的一級預防覆蓋率對HIV在男同中傳播態勢的影響.從表3中可以看出,對易感者有效宣傳教育的覆蓋率bs=0.25與bs=0相比,感染率下降較明顯.但對易感者有效宣傳教育的覆蓋率bs=0.50相比于bs=0.25,感染率的下降效果不顯著.3種情況下模型的傳播閾值R0(見附錄)的均值和標準差如表4所示.從表4中可以看出,當bs=0.25和bs=0.50時,安全套的有效使用率η在[0.50,0.75]內隨機抽樣的情況下,有R0<1,即此時HIV在MSM人群中的傳播能夠成功被抑制.

表3 在不同一級干預力度下北京MSM人群HIV感染狀況預測Table 3 Prediction of HIV infection rate in Beijing MSM population under different intervention

表4 在不同一級干預力度下北京MSM人群HIV感染閾值R0的情況表Table 4 Prediction of threshold value R 0 in Beijing MSM population under different intervention

但若一級預防的效果比較低,即經過一級預防的宣傳教育,MSM人群的安全套有效使用率介于[0.25,0.50]時,3種預測狀況下R0>1均值.由此可見,提高安全套的有效使用率非常重要,若不能實現足夠高的有效使用率,HIV很難得到抑制.這個結果提示政府等有關部門對易感者的宣傳教育不要盲目地投入人力物力,要有針對性地對易感者進行宣傳教育,這樣才能達到最佳效果.

3 討論

本工作中的模型顯示,僅僅對HIV陽性者實現“3個90%”的干預目標(情況2),感染率下降的效果并不明顯.而若對易感者加強宣傳教育(情況3),促使他們提高安全套的有效使用比例,則能使感染率明顯下降.這提醒政府等有關部門,對艾滋病易感者和感染者都應該進行宣傳教育,提高群眾的自我保護以及保護他人的意識,是預防和控住艾滋病的有效方法之一.

值得注意的是:一級干預的效果之一——安全套的有效使用率的作用不可小覷.在MSM人群的有效安全套使用率達到0.50～0.75時,只需有效干預1/4的MSM人群,即可達到控制HIV/AIDS的傳播;而當有效安全套使用率低至0.25～0.50時,則需要有效干預大于一半的MSM人群,才能夠達到阻止HIV/AIDS的傳播.研究結果表明,要重視行為干預的效果,否則可能會事倍功半.

附錄:傳播閾值R 0

在不考慮一級預防,即對易感者進行干預的情況下,也就是說bs=0時,容易找到模型(1)的無病平衡點E10為

為了計算基本再生數R10,利用“再生矩陣”的方法,首先找到模型(1)的f10,v10,FE10,VE10,具體如下:

定理1當R10<1時,無病平衡點E10是局部穩定的;當R10>1時,則E10不穩定.

上述結論表明:當R10<1時,HIV不會傳播;否則,HIV將持續存在.

若考慮對易感者進行宣傳教育,即此時bs6=0時,用上述相同的方法,可以得到模型(1)的無病平衡點為E20=

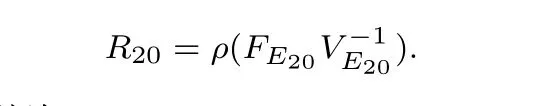
由文獻[5]中定理2,可以得到如下結論.

定理2當R20<1時,無病平衡點E20是局部穩定的;當R20>1時,則E20不穩定.上述結論表明:當R20<1時,HIV不會傳播開來;否則,HIV將持續存在.