基于LBM的單氣泡上升現象及并行優化研究

溫劍鋒，覃一海

（廣西建設職業技術學院，南寧530000）

0 引言

氣液兩相流是非常有趣自然現象，同時也是工業制造中常見的現象。氣泡在液體中產生、合并、上升、爆裂等現象在工業生產中有著重要的影響。在工業生產中，通常根據氣泡的動力學特點，調整生產過程的參數提高生產效率。在醫療中，利用氣泡的運動特性，將藥物運送到患者的生病部位達到治病目的。在航運過程中，通過減少高速運轉的螺旋漿產生的空化氣泡達到保護螺旋漿的目的。

至今，眾多研究者對氣泡上升時出現行為進行展開了深入的研究，如合并、變形、破裂、速度等。Li等人[1]用VOF方法研究了氣泡在液相中產生和上浮。付等人[2]根據氣泡在液體中的運動過程，推導出了氣泡的運動方程。田等人[3]用水平集方法等研究氣泡上升時的變形和運動特點，揭示了氣泡變形的原因。陳等人[4]研究了氣泡在浮力作用下的流場分規律，并提出了浮力作用的假設。

LBM是當前主流的數值模擬方法，它具有算法簡單、邊界易于處理、適合并行處理等特點，非常適合用于復雜多相流現象的模擬研究。CUDA是NVIDIA公司推出的解決復雜運算的架構，它能使GPU在并行運算、圖像處理等方面的能力大大提升。基于CUDA的LBM算法為數值模擬提供了更高效的計算方式，受到眾多學者的喜愛。

本文擬用LBM方法進行建模，然后使用CUDA并行技術對LBM程度進行加速計算，探索氣泡上升的形態變化和上升的速度變化等。

1 LBM建模

1.1 LBM的基本公式

LBM編程簡單主要在于該模型的公式簡單、參數少，本文使用二維LBM模型進行編程，它的基本公式如下：

其中，fi、是分布函數，Ωi是碰撞因子、ei是單位速度、是平衡分布函數(ρ,u)、τ、ρ、u、δt分別是單馳豫時間、宏觀密度、宏觀速度、步長，展開為：

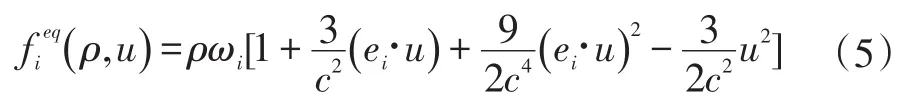
公式（1）包括了碰撞和遷移兩部分，碰撞的公式為：

遷移的公式為：

1.2 LBM多相流模型

經過多年的發展，用于多相流模擬的LBM模型有顏色模型[5]、SC 模型[6]、Zheng 模型[7]，然而這些均存在一些不足，如顏色模型計算具有指數復雜性、穩定性差，如偽勢模型計算虛速度大，Zheng模型不滿足伽利略不變性。在某些研究領域，這些模型的應用受了限制。對此，覃等人[8]深入分析了以上模型存在的缺陷，提出了復合的LBM多相流模型，此模型能更好地進行數值模擬，并具有較高的精確度和穩定性。該模型的動量公式為：

遷移公式為：

上述方程經過一系列的轉化，可恢復N-S方程：

2 模型驗證

本文主要使用（15）公式進行編程模擬，通過計算Δp的值，將實驗計算的Δp值與理論進行比較，以檢測模型的正確性。

其中，Δp表示氣泡內外壓強差，R表示半徑，σ表示表面張力。計算區域定為201×201，界面厚度、氣相密度、液相密度、馳豫時間、表面張力、遷移量、序參等分別為：5、1、1000、0.875、0.1、100、499.5。通過模擬不同的半徑，求出內外壓強差，然后用壓強差與半徑作圖，所得數據如表1表示，由表可見實驗值與理論值非常接近，計算誤差均在1%以下，由實驗可知本文采用的LBM滿足Laplace定律，可用于多相流的數值模擬之中。

表1 實驗結果與理論值對比

3 氣泡上升研究

本文主要模擬二維單氣泡在浮力作用下上升的現象。每一相的密度和表面張力系數的取值與文章Takada[9]一樣。氣泡處于四壁平穩的流場中。初始，氣泡處于計算區域為80×300的低區域中（流場高度的1/4）。氣泡內初始序參設為φ*，氣泡外初始序參設為-φ*。在不同參數值（如表2所示），進行了幾個數值模擬。由于氣泡的半徑很小，我們不必把界面厚設置太大。當浮力和拖拽力達到平衡，氣泡將以幾乎不變的速率上升。事實上，速率并不是常量。氣泡在上升的時候，存在振蕩現象。表2展示模擬結果對比情況。很明顯，這些結果與VOF方法和Takada’s LBM吻合得非常好。氣泡在不同條件下的最終上升的形態如圖1所示。

表2 氣泡在浮力作用下上升的模擬參數

表3 氣泡在浮力作下上升的終點速率

圖1 不同參數下氣泡上升的最終形狀

4 對氣泡上升算法進行加速研究

維度劃分是CUDA優化加速的其中方法之一。Grid和Block是劃分維度的重要單元，通過確定合理的比例使CPU性能發揮最大作用。在優化時，可以將Block劃分一維、二維、三維，通常認為維度越高，能劃分的線程數就越多，但是由于GPU的線程數有限，并不能盲目對Block進行多維度劃分。考慮到計算規模，本文先將Block劃分一維，然后再將Block未利用的空間與Grid重新合并形成新的維度，這樣充分利用了空閑的線程進行運算，使程序并行效率達到最大化。將未進行維度劃分的算法設為S0，已經進行維度劃分的算法為S1，演化10000步的計算結果，如表4所示，由表可見，經過優化加速后，流場越大獲得的加速比越大。因此，進行大規模數值模擬運算時，引入CUDA并行技術能大大提升程序運行效率，能為更深入研究提供堅實的基礎。

表4 方案S0、S1的耗時和加速效果的比較

5 結語

本文使用主流多相流LBM模型研究了氣泡上升的現象，通過多組不同的初始參數計算了氣泡上升的速度以及不同參數下氣泡上升的形狀，實驗與前人研究結果基本吻合。針對當前程序計算效率低下問題，本文引入CUDA對LBM多相流程序進行了加速計算，能獲得最高13.86倍的加速比，大大縮短了程序達到穩定時需要的時間，能為更深入的研究縮短期限。接下來，筆者計劃在CUDA并行技術方面進行更深入的探索，希望能為LBM程序的運算減少更多的時間。