考慮氣象因子的區域電網梅雨期負荷預測

蘇宜靖，谷 煒，趙 依，董 立，蔣 琛，于競哲

（1.國網浙江省電力有限公司，杭州 310007；2.長安大學 電子與控制工程學院，西安 710021；3.浙江大學 電氣工程學院，杭州 310027）

0 引言

我國東南沿海地區每年春、夏交替期間，受副熱帶高壓影響而持續產生降雨的天氣稱為“梅雨天”。梅雨的持續時間、氣溫、濕度及降水量直接或間接地影響著區域電網的負荷情況[1]。短期負荷預測需要綜合考慮這些氣象因子，才能對未來數天的負荷水平進行較為精準的預測。梅雨期是電力負荷由春季較低水平向夏季高峰水平過渡的時期，特別是出梅期前后，氣溫快速上升，負荷也會呈大幅上漲趨勢。較好的短期負荷預測能夠為電力調度部門優化發電機組的配置、合理化電網上下調備用和最優化潮流分布提供重要參考[2]，這直接關系著電網調度的經濟性和安全性。

目前負荷預測的相關算法及手段較為豐富，文獻[3]提出了一種基于L-M優化的BP（反向傳播）神經網絡負荷預測算法，能較好地預測特定日的負荷變化趨勢。文獻[4]引入有效度和相對熵的概念，利用4種預測模型對負荷進行組合預測，具有較高的預測精度。文獻[5]采用模糊化聚類分析方法建立了考慮數值天氣預報下的母線負荷預測模型，為負荷預測的實用化提供了重要支持。這些負荷預測模型及研究方法為本文研究提供了重要參考。

本文統計分析了近兩年某區域梅雨季節氣象條件及負荷變化特點，綜合考慮氣象因子與負荷的相關性。分別建立了基于Elman和BP的2種神經網絡模型，篩選可作為預測樣本的數據節點，對比2種模型預測結果，并深入分析了負荷預測誤差的產生原因。

1 綜合氣象因子與負荷的關系

1.1 負荷特性解析

隨著社會城市化進程的推進，區域電網負荷受氣象因素的影響愈加明顯。特別是沿海地區在出梅期前后，氣溫變化明顯，天氣由陰雨轉為晴朗，對氣象變化敏感的負荷也會有明顯的提升。依據負荷變化特性，可以將其解析為基礎負荷、氣象敏感負荷及隨機波動負荷[6]，如式（1）所示。

式中：p為實時負荷；pb為基礎負荷；pw為氣象敏感負荷；pr為隨機波動負荷。

基礎負荷主要與社會經濟發展水平相關，在較短的時間范圍內體量基本保持穩定，與生產生活的用電規律關系緊密，而與氣象因素關系不大[7]。每年春秋季的氣候條件相對溫和，負荷隨氣象變化相對較小，此時區域電網實時負荷可視為基礎負荷。

氣象敏感負荷是指易受氣象條件影響的負荷，氣象條件包括天氣、溫度、濕度、降水、風速、光照等。每年夏季或冬季，電網空調負荷隨氣象條件的變化較大，此時較春秋季負荷增加的一部分量即為氣象敏感負荷。為了提高梅雨期負荷預測的精確度，應著重考慮氣象因子對pw的影響。

隨機波動負荷是受偶然事件影響而產生的負荷波動分量，包括突發故障、短時限電等，負荷預測可不考慮這類分量。

1.2 綜合氣象因子處理

各類氣象條件因子對電力負荷均會產生不同程度的影響，如夏季氣溫上升導致降溫負荷增大，降雨能夠有效降低氣溫從而降低電力負荷，濕度與風速影響著人體的舒適程度進而影響調溫除濕負荷，天氣條件會影響光照強度，而光照的強弱又影響著光伏出力和照明負荷。由此可知，氣象條件對電力負荷的影響是綜合性的[8]。

為了有效利用各類氣象因子，可以通過CIHB（人體舒適度指數）和THI（溫濕指數）來量化氣象條件[9]。CIHB是指人們未使用保暖或降溫措施時在當前氣象條件下感覺到的舒適程度[10]，計算公式如式（2）所示。

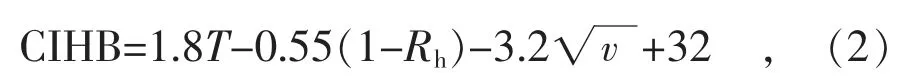
式中：T為溫度；Rh為相對濕度；v為風速，梅雨期可取1.0～3.0 m/s。

THI是一種人為提出用來表示電力負荷與氣象條件之間的關系因子，計算公式如式（3）所示。

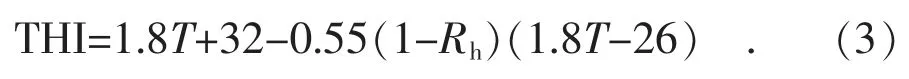
除利用上述指數外，考慮梅雨期多陰雨天氣，光照強度中等，風速較小且變化不大，還應重點關注最高/最低溫度、相對濕度和降水量對日最大/最小電力負荷及電量的影響。

1.3 綜合氣象因子與負荷的相關性

為了研究梅雨期氣象因子對負荷的影響，同時保證預測的正確性與精確性，需要對樣本數據進行相應的處理，即剔除節假日及臺風日數據。以2016年、2017年梅雨期某區域電網數據為例，對比分析了數據處理前后氣象因子與負荷的相關性，詳見表1。

剔除特殊日數據后，負荷與氣象因子的相關程度明顯加深。溫度與負荷相關性最強，是影響梅雨期負荷水平的關鍵因素，負荷隨著氣溫的升高而升高；降水量和相對濕度對負荷的影響相對較小，相關性不強，但大體上也具有降水量越小、相對濕度越大則負荷越高的趨勢；CIHB和THI與負荷具有較強的相關性，兩類指標數值越高，實時負荷也隨之抬高，可作為影響因子來指導負荷預測。

根據上述各氣象因子與實時負荷的相關程度，可以設定3組不同氣象因子的數據源：一是僅考慮日最高/最低氣溫作為負荷預測的單一數據源；二是同時考慮日最高/最低氣溫、降水量、相對濕度因素作為負荷預測的基礎數據源；三是考慮綜合氣象因子作為負荷預測的綜合數據源。在預測模型中支持將單一、基礎和綜合3組數據的預測結果橫向對比分析。

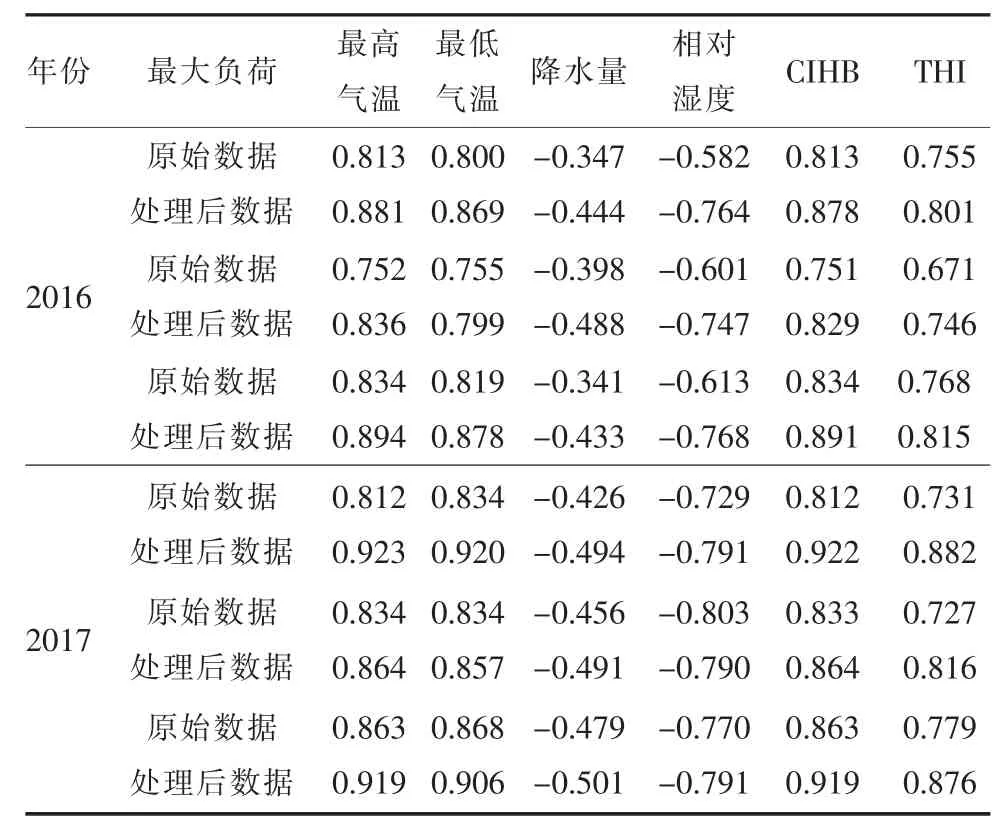
表1 綜合氣象因子與負荷的相關性對比

2 人工神經網絡預測模型的建立

2.1 Elman神經網絡算法原理

與BP神經網絡[11]相比，Elman神經網絡存在一個特殊的關聯層，作用是存儲隱含層單元前一時刻的輸出值，聯接記憶的數據作為下一次隱含層的計算輸入值，模型結構見圖1。這種狀態的延遲效應使神經網絡具備良好的記憶性能[12]。

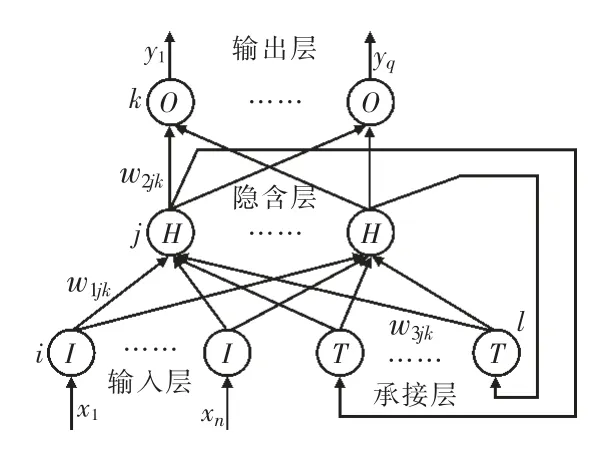
圖1 Elman神經網絡模型結構示意

假設ui，vj，tl，yk分別為輸入層、隱含層、承接層和輸出層的計算結果，則網絡傳遞過程的計算公式如式（4）所示。

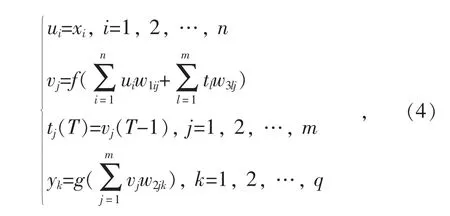
式中：xi為輸入變量；n，m，q分別為輸入層、隱含層和輸出層設置的神經元個數，承接層的神經元個數與隱含層相同為m；w1ij，w2jk，w3lj分別為輸入層i至隱含層j、隱含層j至輸出層k、承接層l至隱含層j的連接權值；T為迭代計算次數；f和g分別為隱含層和輸出層神經元的傳遞函數，可選擇線性函數或sigmoid函數。承接層作用是記錄上一次對應隱含層計算值。

由于Elman神經網絡一般采用與BP網絡訓練相同的梯度下降算法，w1ij和w2jk的修正過程相同，補充w3lj的修正過程如式（5）所示。

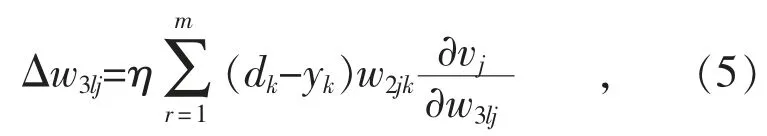
式中：Δw3lj為對應承接層至隱含層連接權值的修正量；dk為目標結果值。

2.2 Elman神經網絡算法流程

Elman神經網絡學習算法流程如圖2所示。

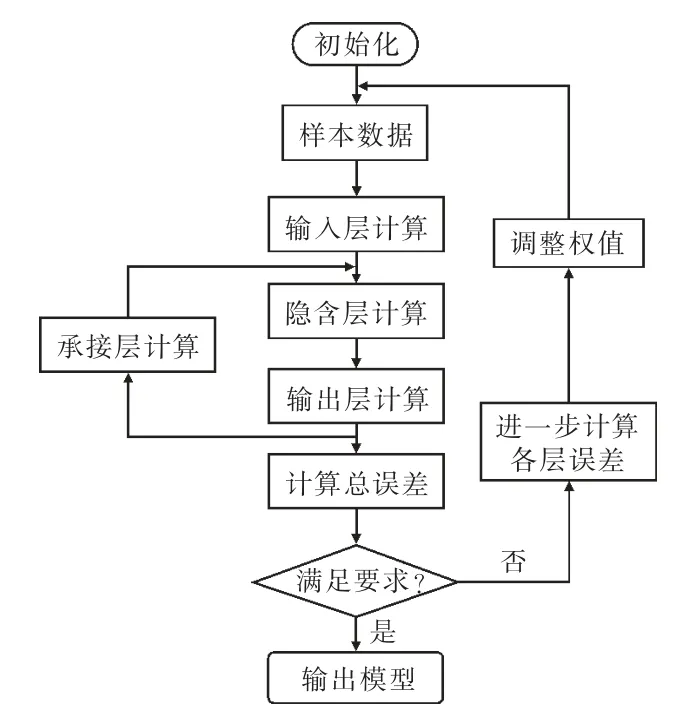
圖2 Elman神經網絡學習算法流程

Elman神經網絡通過內部承接層的反饋作用，存儲并有效利用歷史數據，具備動態響應特性，能夠實現靜態或動態系統的建模，適合于類似持續時間序列的負荷預測[13]。但網絡的訓練過程需要迭代的次數較多，存在收斂較慢的情況。

3 梅雨期負荷預測算例

本文收集了東南沿海某區域電網近兩年的梅雨期氣象及負荷數據。梅雨期區域間的選擇參考省級氣象局發布的入梅和出梅時間，分別為2016-05-25—07-25和2017-06-09—07-13。上述時間段的初始數據均需要經過預處理與篩選，剔除節假日及臺風的影響。在氣象輸入數據上，分別采用了單一、基礎和綜合氣象因子3組數據以作對比分析。在選取預測模型上，分別采用BP和Elman神經網絡算法并選取合適的模型訓練方法。其中，2016年的數據作為負荷預測模型的訓練樣本，在考慮基礎負荷增長并進行適當修正后，將2017年的數據作為測試樣本。

3.1 氣象數據的選取與預處理

相較于工作日，節假日工業負荷與商業負荷的變動較大，直接影響了基礎負荷部分[14]；同時臺風天氣日負荷水平變動較大，對電網而言存在不確定性因素，如線路跳閘、臨時停電等。進行梅雨期負荷預測時可以暫不考慮上述數據，而應篩選出正常工作日的數據作為本次負荷預測的樣本數據，需要剔除節假日與臺風所造成影響的數據。以2016年該區域梅雨期氣象數據為例，氣象數據處理后的結果如表2所示。

為了預防神經元在計算過程中發生數據飽和溢出，應先將模型的輸入量進行歸一化處理，將輸入數據限制在[0，1]，待模型預測完成后對輸出量進行反歸一化處理，以得到負荷預測的結果。數據歸一化和反歸一化計算如式（6）所示。

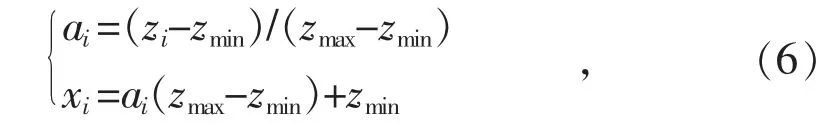
式中：zi為原始數據；ai為歸一化后的數據；zmin，zmax分別為原始數據的最小值和最大值。

3.2 神經網絡模型的訓練

依據上述神經網絡模型的原理與方法，在MATLAB中分別建立雙隱含層的BP神經網絡模型和單隱含層的Elman神經網絡模型。訓練精度均設置為0.001，訓練步長設置為0.001。隱含層傳遞函數均設置為“tansig”的非線性函數，輸出層傳遞函數均設置為“purelin”的線性函數，承接層傳遞函數設置為“purelin”的線性函數。兩者的訓練過程均采用梯度下降算法，以優化訓練過程。

表2 2016年某區域梅雨期氣象數據

選擇負荷預測模型的輸出量均為日最大負荷、日最小負荷、日電量。為了對比不同輸入量對負荷預測結果的影響程度，選取最高氣溫、最低氣溫、日降水量、日平均相對濕度作為基礎氣象因子負荷預測模型的輸入量；選取CIHB和THI作為綜合氣象因子負荷預測模型的輸入量；選取最高氣溫、最低氣溫作為單一氣象因子負荷預測模型的輸入量。

以2016年梅雨期該區域的日電量為例，2種模型的訓練結果如圖3所示。可以發現，無論BP神經網絡還是Elman神經網絡的訓練結果基本擬合了實際日電量的變化曲線。對日最大負荷/最小負荷可以采用同樣的方法進行擬合。

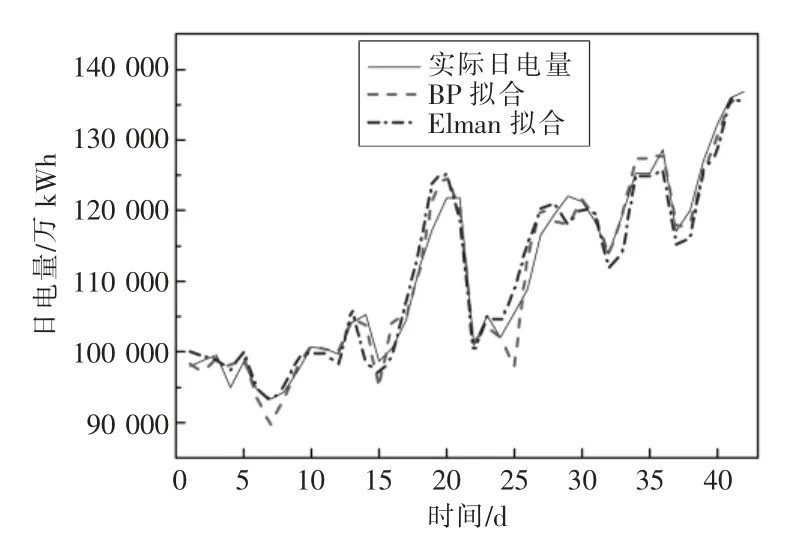
圖3 BP及Elman神經網絡訓練結果

3.3 考慮年度負荷增長趨勢的預測結果處理

隨著經濟社會的發展，負荷水平及日用電量總體呈上漲趨勢。假設2017年相較2016年基礎負荷和氣象敏感負荷的增長比例分別為α和β，則考慮氣象因素后的負荷如式（7）所示。

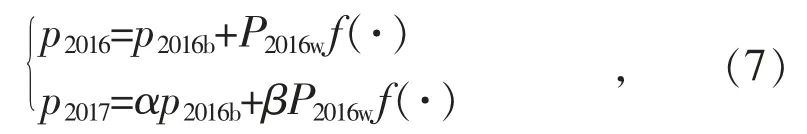
式中：p2016，p2017分別為2016年和2017年的電力負荷；p2016b，P2016w分別為2016年的基礎負荷和氣象敏感負荷；f（·）為氣象影響系數。

神經網絡訓練算法得到的是2016年的負荷數據，考慮年度負荷增長趨勢后，將預測結果進行轉換得到式（8）。

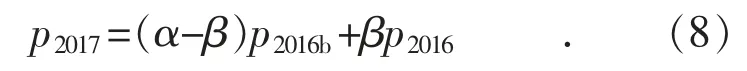
近年來，基礎負荷增長比例α與氣象敏感負荷增長比例β近似等于總體負荷增長比例。利用2016和2017年3—4月每日最大調度口徑負荷按日取平均并相除計算得到，如2016年3—4月的日最大平均負荷約為5 000萬kW，2017年3—4月的日最大平均負荷約為5 200萬kW，則總體日負荷增長比例約為1.04。同理，可計算得到日電量增長比例約為1.08。可代入式（8），修正下一年度的負荷預測結果。

經選擇與預處理后，2017年梅雨期相關氣象數據如圖4所示。

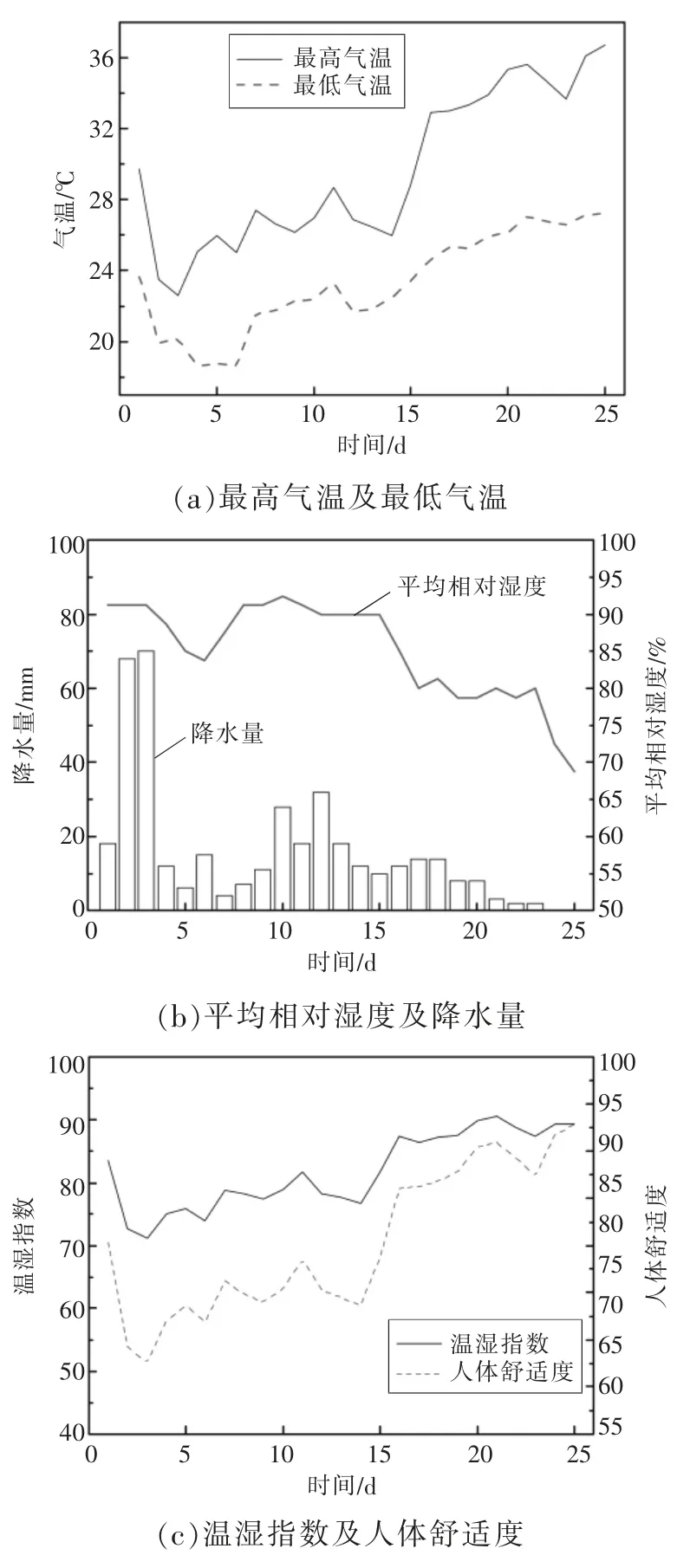
圖4 2017年某區域梅雨期氣象數據

在2種負荷預測模型中分別輸入2017年梅雨期基礎氣象變化數據，并經式（8）換算后，得到日負荷及日電量預測結果如圖5所示。

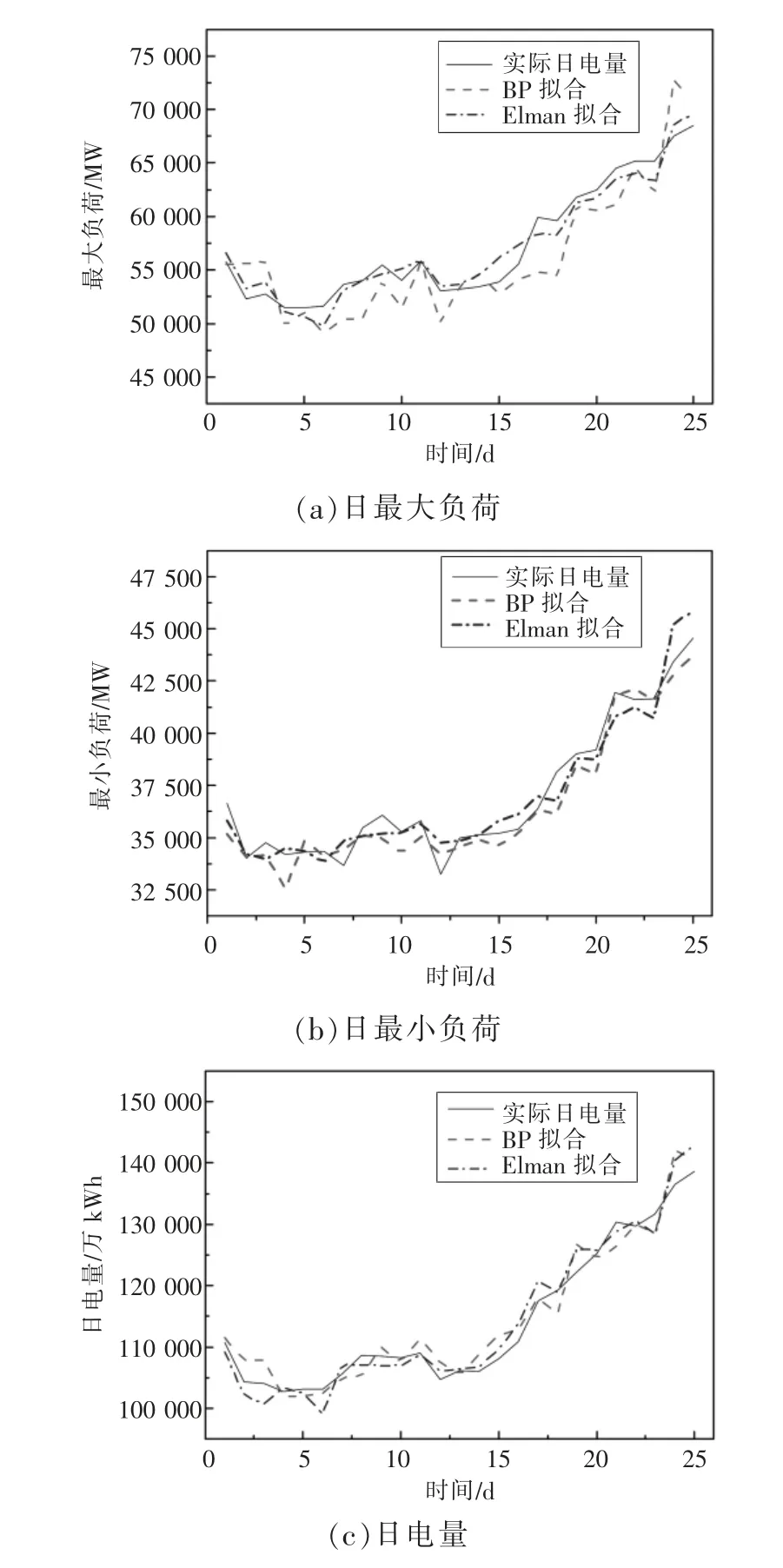
圖5 BP及Elman神經網絡負荷預測結果

結合圖4、圖5可知，從氣象數據上看，剛進入梅雨期，連續的陰雨天氣，降水量驟升，使氣溫開始下降至最低點。隨后氣溫開始回升，濕度下降，溫濕指數及人體舒適度逐漸上升，直至梅雨期結束。從負荷數據上看，剛進入梅雨期，日負荷及日電量下降，并在一定時間內保持一定的水平，隨后在出梅期前后，負荷及電量快速上升，負荷數據變化情況基本上與氣象數據變化一致。結合氣象因子的BP和Elman神經網絡算法對梅雨期的負荷預測結果基本符合實際情況。

4 負荷預測結果分析

為了評價不同神經網絡算法及輸入量對預測結果的影響，需要將預測值與原始數據進行對比，得出誤差后，對預測結果的準確度進行定量分析。

4.1 預測準確度分析與結果評價

選擇合理的誤差評價指標，能夠有效對比不同的預測結果[15]。本文主要采用MAPE（平均絕對百分比誤差）和可決系數法2種方法對負荷預測結果進行準確度分析。

MAPE的計算公式如式（9）所示。MAPE越小，說明預測結果與實際偏離越小，精度越高。

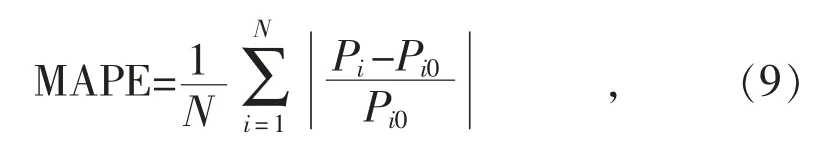
式中：Pi為負荷預測結果數據；Pi0為實際負荷數據；N為樣本數。

可決系數法是通過RSS（殘差平方和）及TSS（總平方和）計算得到的，計算公式如式（10）所示。可決系數R2被限定在[0，1]，結果越靠近1說明預測結果越接近實際結果。

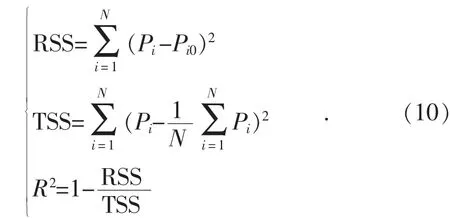
采用不同神經網絡算法及不同輸入量的負荷預測準確度統計如表3所示。

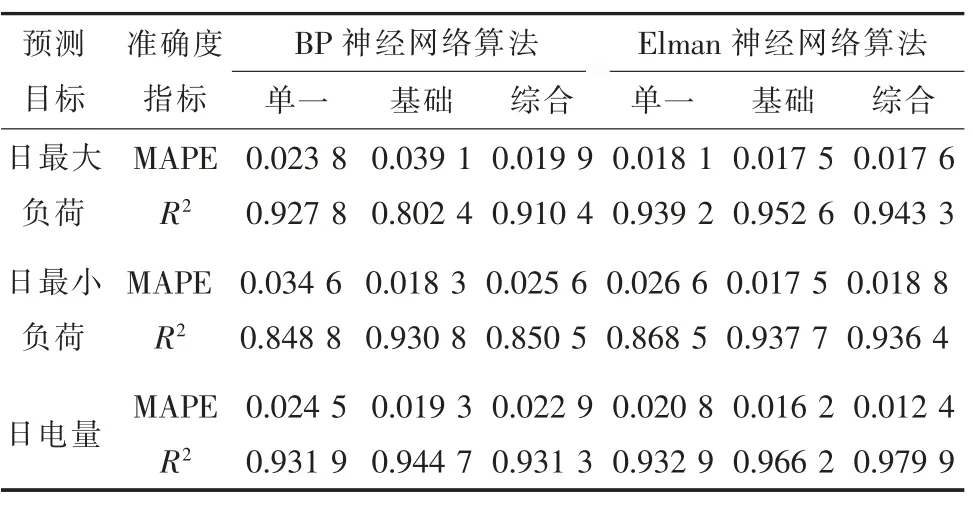
表3 負荷預測準確度統計結果

由表3可知，對于同一種數據輸入量類型，Elman神經網絡算法無論是MAPE還是R2指標都優于BP神經網絡算法，說明Elman算法在梅雨期負荷預測上更具有優勢。在同一種算法下，采用不同的數據處理方法，如運用基礎氣象數據和綜合氣象數據比單一來源數據的負荷預測結果更加精確。對于不同的預測目標，預測日最大負荷及日電量的結果比日最小負荷預測結果更為準確。總體而言，本文提出的Elman神經網絡算法在考慮基礎或綜合氣象因子情況下，對梅雨期日最大/最小負荷、日電量均具有良好的預測特性。

4.2 負荷預測誤差產生原因分析

上述梅雨期負荷預測結果相比實際測得值存在1%～3%的誤差，而短期負荷預測誤差是不可避免的，本文預測誤差的來源主要包括：

（1）歷史氣象數據統計不全面、不精確。本文只考慮了區域電網氣象條件的整體水平，并未對下屬各地區氣象情況進行分時段精確統計，而且存在部分天氣數據缺乏的情況。

（2）神經網絡模型通過歷史負荷數據來推斷下一年的負荷數據，是一種近似的估算，只能反映負荷變化的趨勢，而無法精確計算。

（3）在實際電網運行中，負荷的波動是一種隨機過程，多種外界因素比如突發事故、光伏風電出力驟增都可能對電網產生影響，這些在預測模型中都無法精確考慮。

5 結語

針對區域電網負荷梅雨期前后快速增長的特點，本文提出了考慮氣象因子的區域電網梅雨期負荷預測方法，分別構建了基于BP神經網絡和Elman神經網絡的短期負荷預測模型。以2017年梅雨期負荷水平為例，對比不同氣象因子預測結果的差異，發現考慮基礎和綜合氣象因子數據能夠有效提高預測精度，同時Elman較BP神經網絡算法在MAPE和R2指標上均占優勢。結果表明，本文提出考慮氣象因子的Elman神經網絡負荷預測模型，對梅雨期的負荷具有預測精度高、適應性強、使用價值較好等特點，可用于指導實際負荷預測。