基于學生本位，聚焦高階思維

何佳丹

【摘要】思維是數學學習的重要形式.提升數學核心素養的關鍵是聚焦高階思維發展.要想發展學生的高階思維，教師必須有效設計學習任務，立足學生本位，引導學生超越淺層、被動的學習狀態，使學生展開深度性、批判性、探索性和創造性的自主學習.

【關鍵詞】高階思維;核心素養;有效設計;學生本位

一、高階思維的重要意義

新課程背景下，教育教學提倡以“學科核心素養”為綱，關注學生未來長久發展的素養.數學作為促進學生全面發展的重要學科，一方面要使學生掌握現代生活和學習中所需要的數學知識與技能，另一方面要充分發揮數學在培養學生的科學推理和創新思維方面的功能.由此可見，數學學習離不開思維，思維是數學學習的重要形式，高階思維又是思維的高級形式，因此提升數學核心素養的關鍵是聚焦高階思維發展.高階思維是指創新能力、問題求解能力、決策力和批判性思維能力.培養高階思維能力，能有效促進數學核心素養的落實，提升數學核心能力.

二、從思維發展看當前課堂教學的現狀

1.多

在日常的教學中，教師常受課堂教學時間的限制，為了更好地完成相應的教學內容，課堂中常出現教師講授多、學生表達少的現象或個別師生交流多、全體師生互動少的現象，教師或少數學生的想法代替了全體學生的思維，學生思維多元化發展受限.

2.快

課堂教學進度快是當前數學教學中存在的常見現象.學生剛接收一個新的知識，還未來得及好好消化咀嚼，緊接著快速轉換到下一環節進行更具挑戰的任務.學生沒能獲得充足的探究、思考、分析的時間與空間，容易出現知識鏈的脫節和錯亂.

3.低

探究性學習已經成為當下課堂教學的主流方式.教學中常常看到教師組織學生開展探究性學習任務.在實際活動過程中，多數學生是被教師牽引著被動完成相應任務的，學生缺乏獨立思考、主動探索和批判質疑的精神.這樣的活動僅僅停留在低階思維水平，思維含量低，課堂效率低.

4.少

上述低階思維學習活動的發生，其實是教師缺少高階思維培養意識.學生只獲得對知識的記憶和基本理解，至于獨立發現問題、提出問題、解決問題的能力以及批判、質疑和創新精神，都無法達到.

三、教學實踐：例談培養高階思維的具體路徑

教師和學生共同期待、向往的數學課堂應該是注重高階思維發展，真正關注學習過程體驗的課堂.筆者以人教版六上的“方與圓”練習課為例進行教學，突破常規教學模式，在課堂中聚焦學生高階思維的培養，取得了較好的效果.

（一）有效設計學習任務，指向高階思維發展

為了使數學學習指向高階思維發展，教師需要重組學習內容和結構，精心設計實施教學方案，為培養學生分析、評價、創造三方面的思維能力發展提供充足的空間.

1.開放式素材，培養發散性思維

【教學案例片段1】

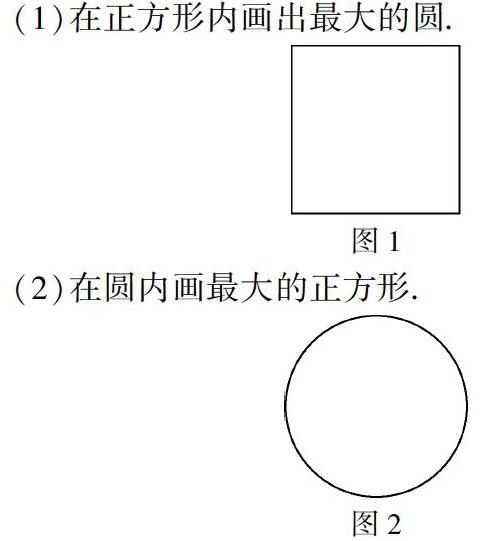
筆者設計了以下兩幅圖，作為“方與圓”練習課的前測作業，請學生按要求畫一畫.

（1）在正方形內畫出最大的圓.

（2）在圓內畫最大的正方形.

圖上沒有任何數據提示，學生需要自己探尋，想辦法通過測量獲得所需要的數據并畫出圖形.在對材料信息的處理中，學生各顯身手，喚起對新課中方與圓的知識的回憶，彰顯個性思維.

【教學案例片段2】

活動探究：我們先來研究圖1這樣的方中圓組合圖形.請利用你手中的組合圖形，算一算正方形和圓的面積比是多少？

組合圖形中沒有數據且大小不同的開放材料的設計恰到好處，教師可以從研究中觀察學生的多元思維.學生運用已有的知識基礎和學習經驗，自行分析現有的和隱含的學習素材，選擇適當的素材.有的學生通過測量數據來進行推導，有的學生不使用具體數據，利用假設法展開推理，即假設半徑是一個具體數，或者用字母r來推算.這些開放式素材的投放，受眾面廣，對不同學生都發揮價值，引發不同思維水平的學生進行深度學習.學生在嘗試中及時有效地觸發其知識、能力的成長，從一種思維到多元思維，使發散性思維得到培養.

2.大任務驅動，激發高階思維萌芽

【教學案例片段3】

師：我們繼續來研究圓中方組合圖形，猜猜看此時正方形和圓的面積還會存在一定的規律嗎？

生：會.

師：你打算怎么研究？ （靜靜等待2分鐘）

交流方法：

生1[]和研究方中圓一樣，先量出圓的半徑，計算面積，再算出正方形的面積，最后求面積比

生2[]要多選幾個數據，用不同數據計算，才能發現規律

生3[]用字母r來表示圓的半徑，計算出正方形和圓的面積

生4[]用字母a表示正方形的邊長，計算出正方形和圓的面積

優化：你們認為哪名同學的方法更有效？說一說理由.

生5：一個個數據計算太麻煩了，用字母表示數，包括了可能的所有數據，結論更具有一般規律性.

實踐：學生嘗試用字母r表示圓的半徑，展開計算和推理.

反饋：S正∶S圓=2r2∶πr2=2∶π.

發現：通過具體數據的計算，我們發現圓中方組合圖形中正方形和圓的面積比總是2∶π.

此處教師設計大任務框架，留白空間，沒有給定提示語和操作步驟等限制，以此激活個體創造性思維，引發學生的多向交流.學生不受按部就班的研究方法和學習步驟的框定，思維就會非常活躍，能夠喚醒內在已有的知識和學習經驗，嘗試尋找有效策略解決問題，多元化思維得以呈現.在大任務驅動下，學生的思維正在逐漸進階，從一類到多類，從特殊到一般，學生的認知也趨于完整、深刻.隨后，教師以恰當而富有啟發性的問題“哪種方法更有效？說一說理由”啟發學生展開深度思考，不斷調整思維.于是，教師在探尋研究方法中，進一步達成一致優化策略解決問題，即用字母表示數來研究最有效，從而形成對這類知識的本質認識，發展學生的高階思維.

（二）立足學生本位，組織促進高階思維的學習活動

數學學習活動的高階思維訓練必須堅守學生本位、學生立場.高階思維重視學生主體的自覺自悟，致力于數學素養的落實.

1.沉淀個體思考，尊重個性化思維

（1）自主探究，彰顯個性化思維，激發創造性思維

高階思維產生于高質量的個體獨立學習.教學案例片段3的研究學習活動中，教師給予學生充足的時間和空間展開自主學習，獨立思考.學生主動經歷猜測、觀察、思考、比較、歸納、實踐、計算、推理等活動，尋找解決問題的策略和方法.在學生個性化的思維得到彰顯后，該研究活動就有多個思考角度、多種解決方法，我們可在異中求同、求佳.此刻，學生的學習不再是停留在表層，也不是被動的狀態，而是展開了深度的探索性學習.在沉思冥想中，學生的創造性思維得到激發，解決問題的數學核心能力真正得以提升.

（2）長時間思考，發展思維的深刻性和全面性

數學學習也需要有靜謐的時光，教師需要在教學過程中適度留白，給學生留有獨立思考的空間與時間，這樣才會有高階思維活動參與進來.

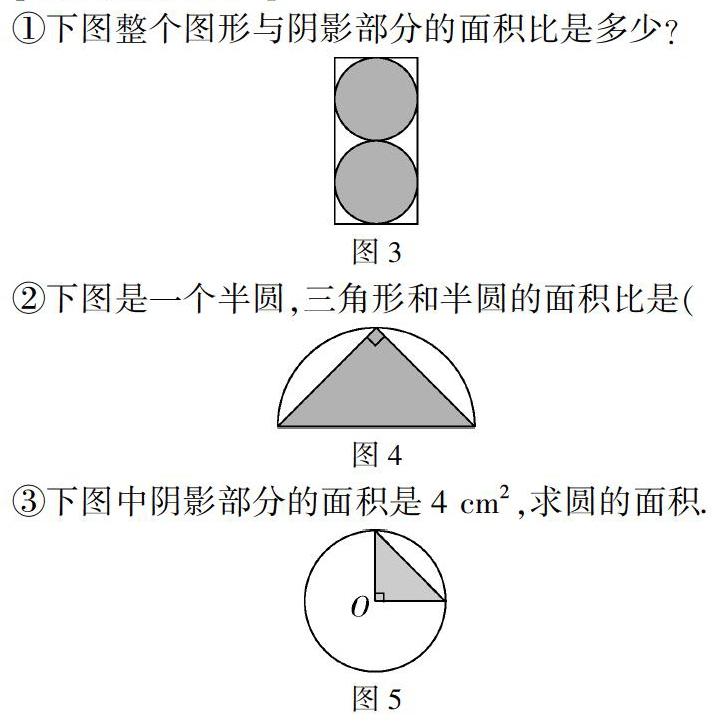
【教學案例片段4】

①下圖整個圖形與陰影部分的面積比是多少？

②下圖是一個半圓，三角形和半圓的面積比是（?）.

③下圖中陰影部分的面積是4 cm2，求圓的面積.

通過對方中圓和圓中方組合圖形的加工和改造，教師設計了三道變式練習.習題①是方中圓擴大2倍的結果，習題②是圓中方縮小為原來的二分之一，習題③是圓中方的更高階變式.三道習題思維梯度高，具有一定挑戰性.此類問題要求高，要給學生較長的時間進行充足的思考、分析和解答.長時間思考難題，使學生的思維發生觸動，喚起對前后知識之間的關聯;尋找知識的脈絡，發現來源是圓中方或方中圓基礎圖形;在變中抓不變，應用于變式題中，最后解決問題.長時間的思考，使學生開啟了深度學習的大門.學生經歷了個體獨立思考的操作過程，對問題的解決有了自己的體驗與想法.在長時間的思考過程中，學生的思維深度參與且變得全面和深刻，挑戰了高階思維，問題解決能力也相應得到提升.

2.分享集體經驗，促進思維拓展

課堂教學既要關注個體發展，也要面向全體，鼓勵全員共同參與，形成學習共同體，展開師生互動和生生交流.集體經驗和方法分享的形式讓不同觀點和思維得到充分尊重和重視，使學生能更好地理清自身的邏輯思維，提升語言表達能力，發現解決問題的有效策略.

在方中圓組合圖形面積關系的研究環節中，學生基于獨立思考后，再進行精彩的經驗分享.學生在多種方法辯論中進行思辨，經歷質疑、討論、批判和關聯，最終明確用字母表示數獲得的結果更具一般結論性，且更加高效.練習環節，在學生完成后，教師組織學生說一說各自的想法.習題③是圓中方的更高階變式，對學生來說更具挑戰，是發展高階思維的關鍵處.教師可以在與學生交流中看到每種方法背后學生的知識基礎和思維水平.有學生對圖形的面積公式十分熟練，利用三角形面積公式求出r2，進一步通過圓的面積公式求解圓面積.也有學生則是學會了應用本節課圓中方的知識，自主解決問題，即將圖形補充還原成圓中方，由三角形面積推導出正方形面積，再借方與圓的面積關系，通過份數計算出每一份的大小，最后算出圓的面積.這兩種方法均體現出學生已經較好地掌握了本課的新知，并能夠自主運用解決相關的問題.學生的思維和能力都得到一定發展.學生不需要將圖形還原成完整的圓中方，僅在四分之一圓中方中依舊可以運用2∶π的面積關系推算四分之一圓的面積，最后回歸到求整圓面積.

在有效的集體互動中，學生分享交流的內容更趨于全面和深刻，學生在傾聽中獲得了更多的思考，拓寬了對本題相關知識和方法的認知領域，促進了思維品質的提升與拓展.

四、結束語

隨著課堂教學的不斷優化和發展，增強運用高階思維指導教學活動是每位教師都應該探索和努力的方向.數學學習不是簡單地把知識塞進學生的頭腦中，而是讓學生的思維活躍.教學的最終指向是關注學生的長遠學習，讓學生學會思考、學會質疑、學會分析、學會創新，獲得學習的方法和思考的模式.要想發展學生的學習能力，落實核心素養，就必須重視培養學生的高階思維.

【參考文獻】

[1]王瑩.“高階思維”與學生數學“深度學習”[J].數學教學訊，2018（19）：13-14.

[2]程明喜.小學數學“深度學習”教學策略研究[J].數學教育學報，2019，28（4）：66-70.

[3]袁愛國.高階思維與語文深度學習[J].教育研究與評論（中學教育教學），2017（11）：5-11.

[4]馮幼絨，孫天山.基于問題的高階思維教學研究[J].化學教與學，2016 （5）：2-4.