基于雙時間窗的多設備串行系統機會維護策略

（上海交通大學 機械與動力工程學院，上海200240）

隨著機械加工系統自動化程度的逐步提升，預防維護對于系統生產效率的保障作用愈加突出，尤其在串行系統中，任一設備的失效都易引起生產線的整體停機.因此，制定有效的預防維護策略以保障多設備串行系統高效運行，是目前維護領域的研究熱點.

考慮操作便利性，傳統的面向多設備機械加工系統的維護研究一般采取定周期的整體維護策略[1]，可有效地減少系統的維護停機次數.然而，在實際生產中，多設備串行系統的設備之間因衰退特性存在明顯差異，定周期的整體維護策略無法統籌各設備的個性差異.針對這一問題，周曉軍等[2]提出了機會維護策略，基于設備衰退差異進行組合維護，在減少系統停機次數的同時有效節約了成本.

目前，機會維護研究可分為2類：基于動態決策的機會維護策略和基于規則的機會維護策略.動態機會維護[3－7]通常采用短時決策，可更好地反映設備的即時衰退差異，但決策時需枚舉可能的維護方案，算法復雜且計算量大，一般適用于由少量設備組成的生產線.基于規則的機會維護通常采用長時決策，目標為制定一種適用于全規劃期的靜態機會維護規則，進而基于這一規則獲得維護方案.如Xia等[8]使用維護時間窗對串行系統的維護作業整合至最先到達的設備最優維護時刻，以降低系統的整體維護成本.朱傳軍等[9]通過判斷機器維護和加工所占用的時間是否沖突來進行決策，在兩者沖突時將維護操作盡量提前到前一道工序末尾或者機器開始加工的時刻.Ding等[10]采用基于設備性能狀態的維護機會窗策略整合風力渦輪機的各部件維護活動，將參與機會維護的設備的維護時刻提前.Zhao等[11]通過構建維護閾值函數，提出了更為合理的維護機會窗表征方式.由于基于規則的機會維護策略判定過程簡單，且不受設備數量約束，相對于動態方法，其操作性更強，在企業中應用也更為廣泛.

但是，目前基于規則的機會維護研究成果多在確定當前周期的維護組合后，將組合內各設備都提前至與該周期內最先達到最優維護周期的設備同時維護，意味著除了最先達到維護閾值的設備是按期執行維護活動的，其余設備均為提前，存在一定的不合理性.事實上，從Lin等[12]研究中可以發現，在不同設備的最優維護周期前后時間范圍內，維護成本隨周期長度變化的幅度較為平緩，且對周期延長遠小于對周期縮短的敏感性.這表明，在一定范圍內將最先達到最優維護周期設備的維護活動適當推后，對該設備在當前周期內的成本影響較小，卻可有效降低規劃期內系統整體的維護成本.

本文以多設備串行生產線為研究對象，提出一種基于雙時間窗規則的機會維護決策模型，將傳統單窗策略中以達到單設備最優維護周期這一停機條件，改為將此作為維護決策觸發條件，通過時間窗規則合理推后最先達到最優維護周期設備的維護活動，以獲取比單窗策略維護總成本更優的維護策略.

1 問題描述和維護策略

串行系統由m臺設備組成，ti，j為設備j執行第i次維護的時刻，對應系統整體進行第r次維護所在時刻tr，即ti，j＝tr.設備衰退特性各異，系統整體停機時并不一定對每臺設備均進行維護，因此設備維護計次i和系統維護計次r始終滿足i≤r.W為表征設備維護組合的時間窗，w為表征維護時機決策的時間窗.

假設：① 生產過程和生產環境相對穩定；② 生產線連續生產，各設備均不含緩沖區；③ 任一設備的失效都將觸發小修；任一設備進行預防維護，整條生產線都將停機；④ 小修不改變設備故障率，僅使設備恢復運轉，預防性維護修復非新；⑤ 小修時間和預防維護時間均忽略不計.

假設維護規劃期為[0，T0]，通過最小化規劃期內多設備串行系統的維護總成本Csys，獲取串行系統的最優機會維護策略.決策過程如下：

（1）系統初始化，從零時刻開始運行；

（2）以各設備當前維護周期內維護成本率最低為目標函數，獲取設備j在當前維護周期的最優維護間隔T＊i，j，進而得到單設備的最優維護時刻t＊i，j；

（3）以當前系統內最早到達最優維護間隔的設備為準，其最優維護時刻作為現階段的系統維護決策觸發點，即W的起點時刻，記為t＊r，令最優維護時刻落在時間區間[t＊r，t＊r＋W]內的設備參與本次機會維護；

（4）同樣，以t＊r作為w的起點時刻，則第r次系統機會維護的最終維護時刻tr＝t＊r＋w；

（5）維護活動實施，更新設備狀態，系統繼續在規劃期[0，T0]內運行；

（6）步驟（2）～（4）保持運行直至規劃期結束，搜索使規劃期維護總成本最低的W和w取值，即可得到系統的最優維護策略.

2 維護建模和決策

2.1 維護建模

根據上述決策過程，系統的維護建模主要分為兩步.首先，以所在周期內設備的維護成本率最低為目標，構建單設備維護模型，獲得系統中設備各自的最優維護周期；其次，以系統在規劃期內的維護總成本最低為目標，構建系統整體的維護模型，進而基于雙時間窗規則獲得最優的維護策略.

2.1.1 設備最優維護周期決策建模 傳統等周期預防維護建模中常假設預防維護可使設備修復如新[13]，而事實上，設備隨著役齡的增加會產生一些不可修復的退化因素.為表征設備的固有退化過程，本文引入修復非新因子θ表示修復效果，由于退化特性，設備在每次修復完成后都能夠繼續保持運行，但其運行狀態不會比前一次修復完成時更優，所以θ在區間（0，1）上取值.設備狀態用虛擬年齡來表征[14－15]，假設Ai，j表示設備j在第i次維護后的虛擬年齡，則該設備在第i＋1次維護后的虛擬年齡可表示為

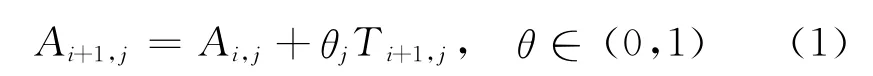
式中：θj表示設備j的修復非新因子；Ti＋1，j表示設備j的第i＋1個維護周期.

設備的維修活動通常分為小修和預防維護，這意味著維護周期Ti，j中產生的維護成本包括小修成本和預防維護成本.此外，設備進行預防維護時會造成生產線的整體停機，因此每個維護周期中還應包含生產線的停機成本.在此基礎上，單臺設備j在第i個維護周期中的維護成本率可表示為

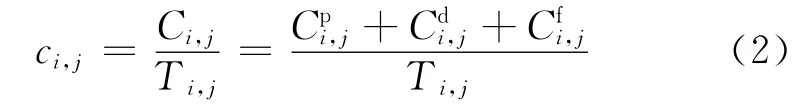
式中：Cpi，j為設備j第i個維護周期的單次預防維護成本，假設同一設備每次的預防維護成本保持不變，則等于相應設備的單次預防維護成本，即滿足Cpi，j＝Cpj；Cdi，j為預防維護引發的系統整體停機成本，其對任意設備均相同，等于每個周期的停機成本，即滿足Cdi，j＝Cd；Cfi，j為設備j在第i個維護周期的累計小修成本，其與設備j的單次小修成本Cfj以及第i個維護周期中的累計故障次數ni，j相關.式（2）可改寫為

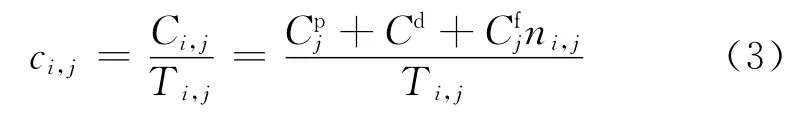
若用λ（t）表示設備的故障率函數，由于其服從連續分布，設備j在第i個維護周期中的累計故障次數可表示為

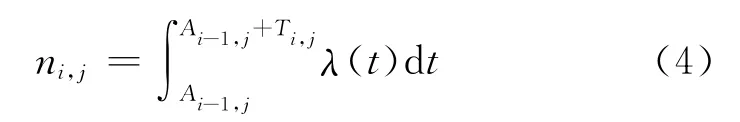
式中：Ai－1，j表示設備在第i－1次維護后的虛擬年齡；Ai－1，j＋Ti，j表示設備j在第i次維護前的虛擬年齡；Ti，j為決策變量，Ai－1，j的值由式（1）推導可得.

綜上，單臺設備j在第i個維護周期中的維護成本率可改寫為

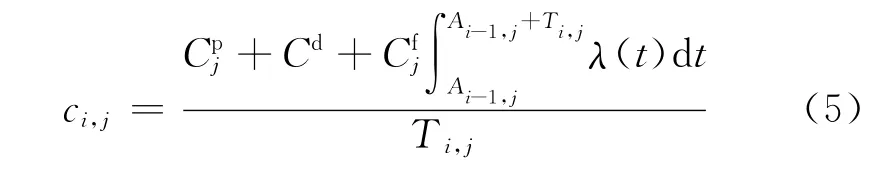
以 min｛ci，j｝為目標函數進行求解，即可得到設備j在第i個周期的最優維護周期T＊i，j.

2.1.2 系統最優維護策略決策建模 串行系統規劃期內的維護總成本為系統中各設備維護成本的累加和，即系統維護總成本同樣由小修成本、預防維護成本和停機成本組成，可表示為

(1)課程內容的整體性。教師需要在第一次授課時，整體上介紹課程內容，讓學生了解整門課程信息，不要形成碎片化知識。這就需要教師十分熟悉課程的能力培養目標，了解每一堂課的教學目標，同時也需要清楚知識體系的前后邏輯關系，讓學生對所學知識形成一個詳細的脈絡。《計算機網絡技術實訓》課程，需要老師在第一次授課時向學生講解計算機網絡架構，讓學生知道每次學習的都是其中一層的知識點。

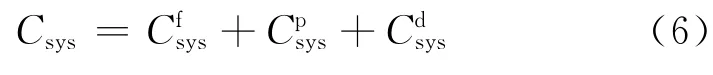
式中：Cfsys為系統規劃期內的小修成本總和，與系統中設備數量m、規劃期內各設備累計故障次數njf以及Cjf相關；Cspys為預防維護成本總和，其與m、規劃期內各設備預防維護次數njp以及Cjp相關；Cdsys為停機成本總和，每次預防維護都將造成系統整體停機1次，因此Cdsys僅與Cd以及系統整體停機次數nsdys相關，而與m無關.式（6）可改寫為

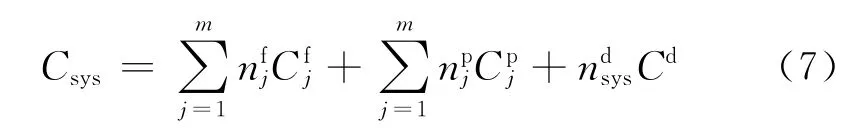
結合式（1）和（4），設備j在規劃期內的累計故障次數可表示為

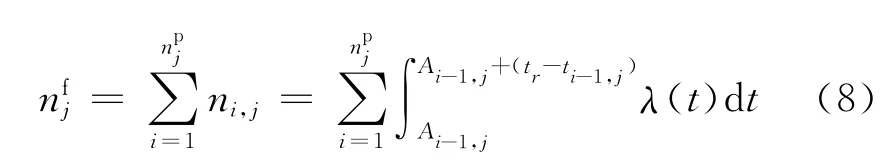
式中：Ai－1，j＋（tr－ti－1，j）為設備j在系統的第r個維護階段前的虛擬年齡.

結合式（7）和（8）可以得到系統在規劃期內的維護總成本

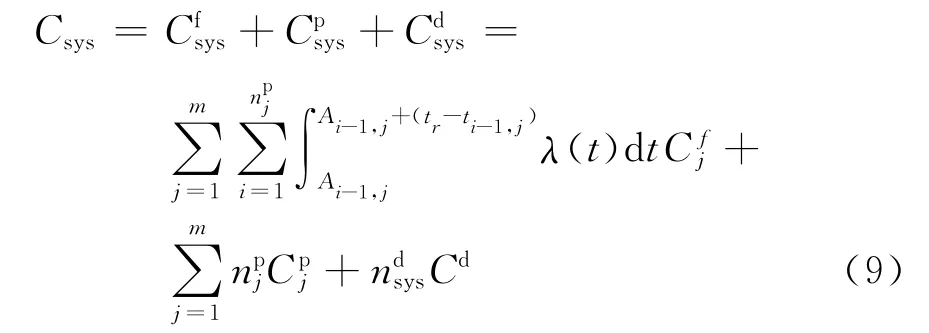
以總成本Csys最小為最終目標函數進行求解，即可得到w和W的最優值，即系統的最優維護策略.

2.2 基于雙時間窗的維護決策

多設備串行系統的維護周期是系統從本次維護的起始時刻到下一次維護的起始時刻之間的時間間隔.基于設備的最優維護周期模型可得到設備j在設備自身第i個維護周期內的最優維護間隔Ti，j，結合設備第i－1次實際維護時刻ti－1，j，則t＊i，j＝ti－1，j＋Ti，j，即為設備j在第i個維護周期內的最優維護時刻.同時，根據假設，該設備維護周期i對應系統的第r個維護階段，因此，t＊i，j亦為設備j在系統第r個維護階段內的最優維護時刻.

在此基礎上，為減少系統停機時間，節約停機成本，需將設備維護操作進行有機整合.如圖1所示，可使用維護組合時間窗來確定設備的機會維護組合，該時間窗所在區間[t＊r，t＊r＋W]即為系統在第r個維護階段內的機會維護范圍.當該階段內最優時刻滿足ti＊，j≤tr＊＋W時，設備j進行機會維護；否則，不對設備進行任何操作.

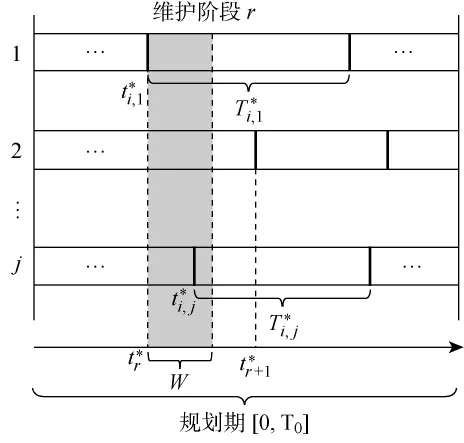
圖1 維護組合時間窗示意圖Fig.1 Maintenance time window for unit grouping

確定系統第r個維護階段內的維護設備組合后，進行該階段維護時刻的決策.在傳統的單窗策略下，維護時刻的確定方式如圖2（a）所示，直接以tr＊作為停機時刻，其余進行機會維護的設備在該時刻同時進行維護.圖2（b）所示為在雙時間窗策略下的維護時刻決策，以tr＊為決策觸發點，引入w，表示設備的實際維護時刻自tr＊向后偏移w，得到tr＝tr＊＋w作為系統在該維護階段的最終維護時刻，偏移量w為決策量.對比不同w值下的系統維護總成本，取其中令總成本最低的w值為最優解w＊，進一步得到串行系統最優維護時刻tr.

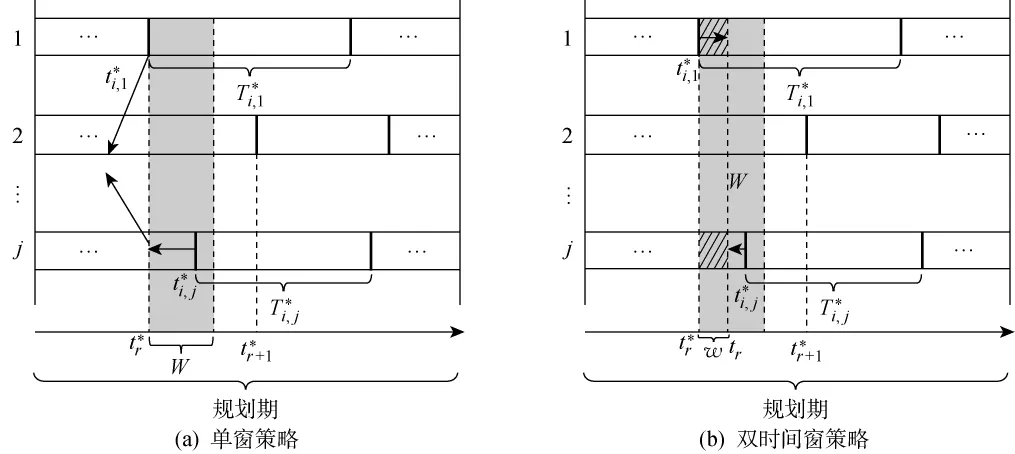
圖2 維護時機時間窗示意圖Fig.2 Schematic diagram of maintenance time window

3 算例分析

3.1 算例概覽和策略對比

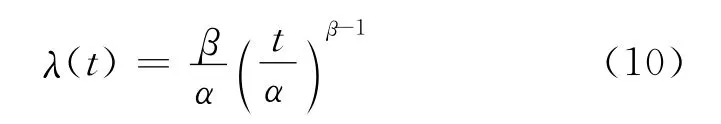
式中：α和β分別為Weibull分布中各設備的尺度參數和形狀參數，可由這3臺設備各自的歷史故障數據擬合得到.設備參數如表1所示.

為獲得雙時間窗規則下系統的最優維護策略，基于MATLAB對系統進行數值模擬.具體決策算法實現流程如圖3所示.

圖3中，維護模型的決策變量為W和w：W取值以設備最優維護間隔為依據，通過模擬得知，一般情況下設備的最優維護間隔在30d天左右，因此令W取值范圍為[0，30]d，搜索步長為1d；大量的模擬實驗得到w最優取值一般不超過8d，因此令w取值范圍為[0，8]d，搜索步長為1d.在維護階段r的決策過程中，若t＊i，j滿足機會維護條件，即t＊i，j≤t＊r＋W，則在這一階段對該設備進行預防維護，并更新設備自身的維護周期i＝i＋1；否則，設備自身的維護周期不改變.對系統內所有設備決策完成后，計算實施維護的時刻tr＝t＊r＋w，并更新系統維護階段r＝r＋1.

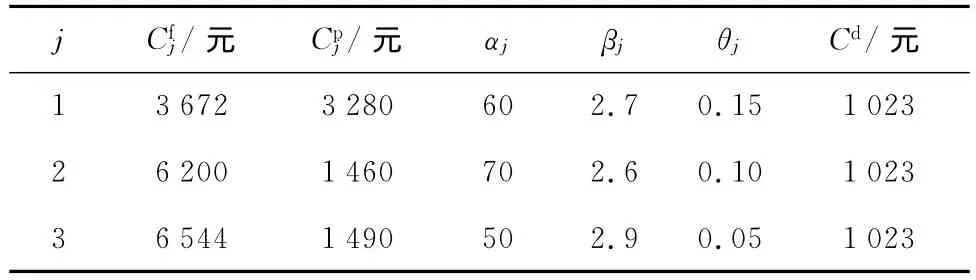
表1 設備參數Tab.1 Equipment parameters

圖3 基于雙時間窗系統的決策邏輯框圖Fig.3 A decision flow chart based on dual time window system

為充分體現雙時間窗策略在機會維護決策中的有效性，本文設置了基于單時間窗的對照策略進行比較.假定單窗策略在同一生產線上實施，設備參數條件均保持不變.相比于雙窗策略，單窗策略只設置了W，即僅判斷某設備是否進行機會維護，而維護時機不進行尋優，直接采用t＊i，j作為系統機會維護的停機時刻.在系統的第r個維護階段內，單窗策略首先計算出t＊i，j，若t＊i，j－t＊r≤W＊，則判斷設備j在該階段進行機會維護，最終維護時刻直接定義為t＊r.

MATLAB模擬結果顯示：單窗策略下，當W＊＝17d時，可以獲得最低系統維護總成本C′sys＝136 530元；雙窗策略下，當W＊＝12d并且w＊＝2d時，系統獲得最低維護總成本Csys＝135 620元；可見雙窗策略在維護成本方面優于單窗策略.表2為雙窗最優策略下系統在規劃期內的維護時刻表，表示系統在1～12個維護周期中的停機時刻，其中，“／”表示在對應周期中j不參與機會維護.

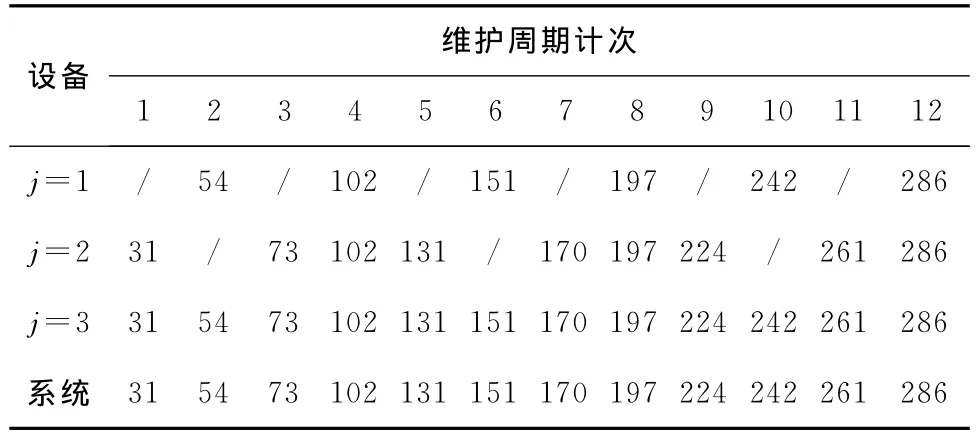
表2 系統維護時刻表（W＊＝12d，w＊＝2d）Tab.2 System maintenance timetable（W＊ ＝12d，w＊ ＝2d）

3.2 不同停機成本下的策略對比

對于串行生產系統，設備同時維護可有效減少系統的維護停機次數，進而降低停機成本，因此，停機成本的變動是影響機會維護決策的主要因素，也會直接影響雙時間窗策略的應用效果.為了驗證雙時間窗策略的有效性，在上述串行系統中，令設備的其他參數保持不變，停機成本在400元到3 400元上均勻取值，對雙時間窗策略和單窗策略分別進行實驗，結果如圖4所示，兩種策略下的最優總成本都隨著停機成本的增大而增大.對兩類成本進行具體對比分析，可以發現：僅當Cd為1 400元左右時，兩類規則下的最優總成本有少量重合的現象；其余情況下，雙時間窗策略得到的維護總成本總是低于單窗策略，這進一步表明了雙時間窗策略的優越性.

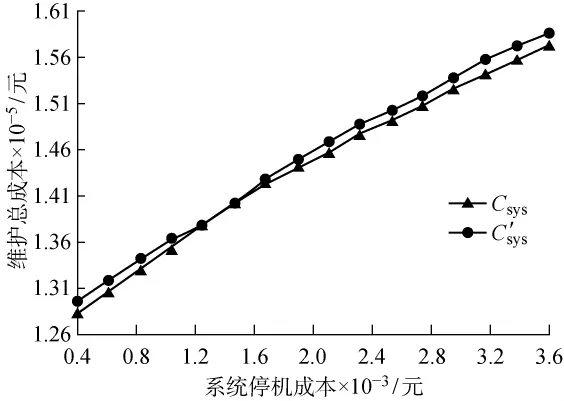
圖4 維護總成本與停機成本關系Fig.4 Relationship between total maintenance cost and shutdown cost

此外，隨著停機成本的增大，雙窗策略下最優組合時間窗W＊的變化如圖5所示，在一定范圍內，停機成本越大，W＊值越大.這是因為隨著停機成本上升，需要通過增大維護組合時間窗使各設備盡可能地同時維護，以減少系統的整體停機次數，這一結果與實際生產情況相一致.圖5亦顯示，當Cd增大到一定數值，W＊取值將趨于平緩.以Cd＝3 200元為例，該條件下W＊＝24d，系統的最優維護時刻如表3所示.此時3臺設備的維護時刻完全一致，即每次機會維護決策時，所有設備都將同時進行維護.這說明，當W＊取值足夠覆蓋所有設備時，停機成本的變動將無法繼續影響設備的維護動作，此時W＊取值將趨于穩定.

圖5 維護組合時間窗與停機成本關系Fig.5 Relationship between maintenance combinition time window and shutdown cost

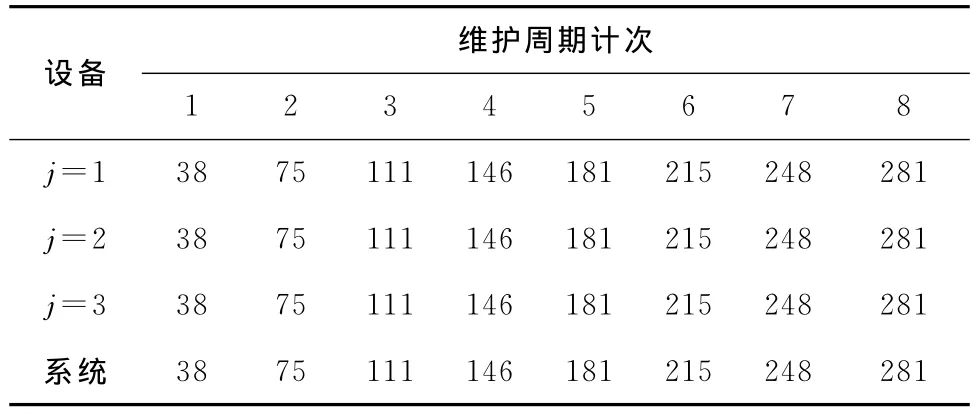
表3 系統維護時刻表（Cd＝3 400元，W＊＝24d）Tab.3 System maintenance timetable（Cd ＝ 3 400yuan，W＊＝24d）

3.3 其他成本參數下的策略對比

生產線設備的種類繁多，其維護成本及小修成本也各不相同.以3.2小節實驗的參數環境作為基準組，定義小修成本及預防維護成本兩類參數分別為引入變化因子令成本參數通過調節兩者對應的變化因子的大小，得到不同的成本參數組合.

在基準組的基礎上，保持其他參數不變，僅調整h1和h2的值進行數值實驗，結果如表4所示，在和Cpj按照不同比例放大或縮小時，雙時間窗策略所需的維護總成本仍優于單窗策略.

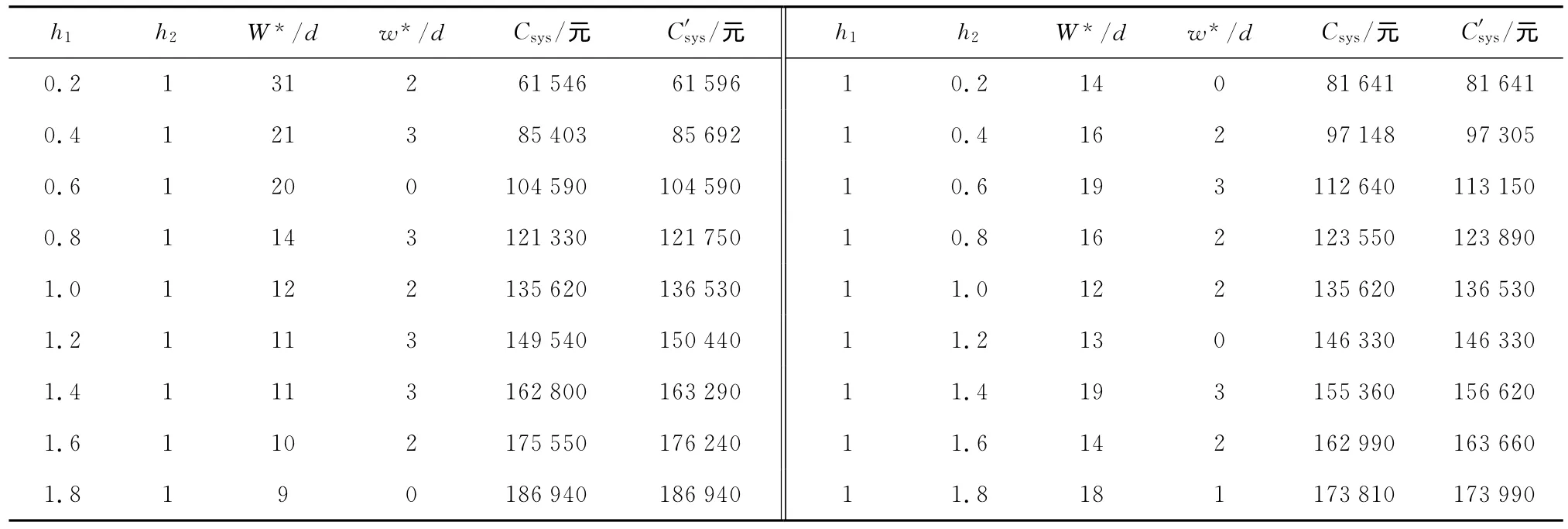
表4 不同h1和h2時的實驗結果Tab.4 Experimental results with different values of h1and h2

3.4 設備數量增加時的策略對比

表3和4的實驗結果驗證了不同設備類型條件下，雙窗策略在三設備串聯生產線中相對于傳統單窗策略的有效性.然而，在實際生產中，各生產線上的設備不僅類型不同，其數目也隨著生產工序的復雜程度改變.在表1所示基準組的基礎上將設備數量增至8臺，具體參數見表5.在單窗策略和雙窗策略下分別進行實驗，結果顯示：在單窗策略中，當W＊＝19d時，得到C′sys＝402 160元；在雙窗策略中，當W＊＝18d且w＊＝1d時，得到Csys＝401 630元，顯然優于單窗策略，即雙時間窗策略在設備數量增加的條件下依舊有效.

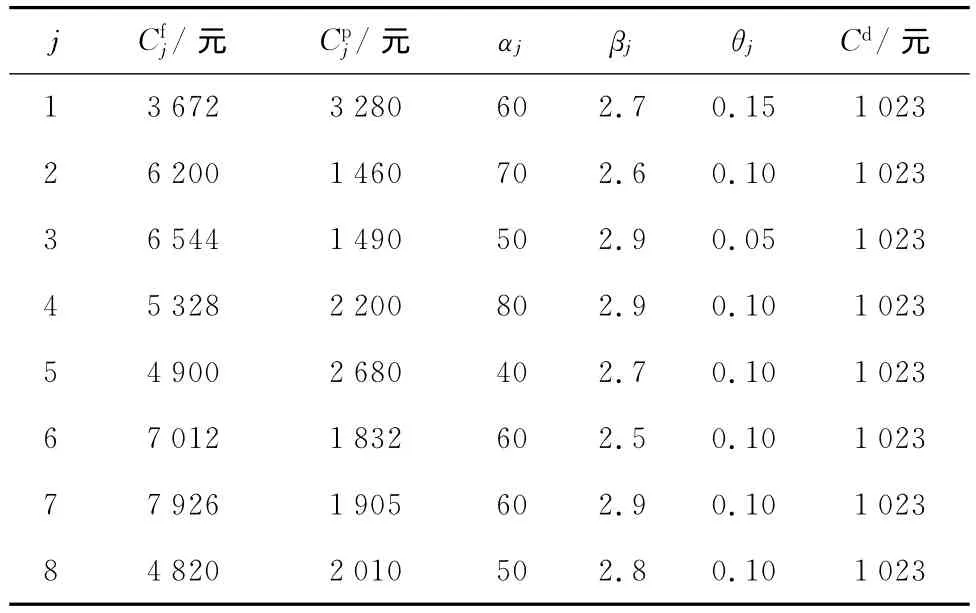
表5 不同參數下8臺設備生產線實驗結果Tab.5 Experimental results of eight units with different parameters

4 結語

本文基于傳統的單時間窗機會維護策略，引入多設備串行系統維護時刻的優化機制，提出基于雙時間窗規則的機會維護策略.對設備和系統分別進行維護建模，在此基礎上利用維護組合時間窗對設備的維護活動進行整合，利用維護時機時間窗對系統維護時刻進行優化.算例分析結果表明，在復雜的參數環境中，相對于單窗策略，雙時間窗策略在大多數情況下可以獲得更低的系統維護總成本，具有廣泛的適應性與穩定性.