核心素養理念下，在初中數學課堂中如何進行有效追問

陳滿興

摘要：在國家倡導素質教育和新課改背景下，“追問式”教學成為當前教學模式探索和創新的理論及實踐訴求。在數學教學實踐中，教師運用藝術的手法精心設計，實施課堂追問，既能對學生思維作即時的疏導、點撥，促進學生積極思考，主動探索，實現“有效學習”，又能實現教學目標的基本控制，使課堂教學效果最優化，從而促進學生的全面發展。

關鍵詞：核心素養;數學課堂;有效追問

隨著數學課程改革的深入，學生核心素養的培養越來越受到重視。核心素養是基于數學知識和技能，但又高于具體的數學知識和技能。核心素質是數學學習中數學和數學思想的本質。課堂應該是對話性的課堂，課堂追問是課堂師生對話的重要方式，在數學課堂教學中起著紐帶作用，好的追問能暴露學生真實的思維進程，便于教師把握教學，將學生思維引向深入，引導學生更為深入地理解數學本質，進而提升學生的數學素養。那么，如何實現數學課堂教學追問的有效性呢？

一、精心設計“有效追問”

在初中數學課堂上，往往會出現“滿堂問”的活躍課堂，但其教學效果低下的現象，究其原因，主要是提出的問題沒有從教學目標出發，隨心所欲地問。這樣，學生雖然積極參與了問題的交流，但問題脫離了目標，這樣的討論既不利于學生對知識的理解，也浪費了時間。為了避免出現“隨心所欲、漫無目的”的滿堂問”的活躍課堂現象，教師在備課時，要先把教學目標的要求分解成幾個小目標，然后根據分解的小目標設計幾個連續性問題進行有效的追問，這樣利于學生更好地理解和掌握所學的知識。如在設計講授《弧、弦、圓心角》時，我課前精心設計了以下的“追問”：1.認真觀察一下在同圓中，弧、弦、圓心角三者有何關系，試動手操作、探究一下，看看自己所歸納的性質與教科書的有何異同？2.在等圓中三者又有何關系？3.不在同圓、等圓中，三者又有何關系？ 這樣逐步設計追問，能把本課的教學目標分化，讓學生在已有認知結構的基礎上構建新知識，從而達到基礎知識的自然形成，并建立數學概念，便于數學課前自主學習，提高效率。

二、將學生思維引向深入進行有效追問

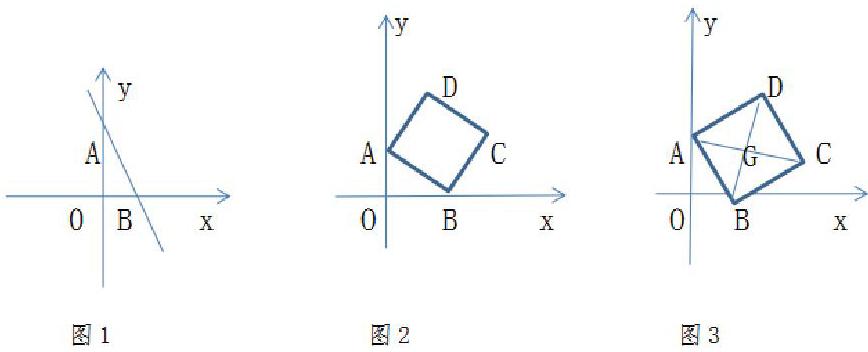
“跳起來摘桃子”，才能摘取長在高處、色香味俱全的“桃子”。在教學過程中，我們發現有部分學生學完新知后仍是一知半解，似懂非懂，顯然這部分學生對所學知識并沒有進行消化吸收，一知半解。為了解決學生“知其然不知其所以然”的現象，在教授時，我們應該將一個個難點設計成一組組帶有梯度的小問題，通過循序漸進，層層深入的“追問”，刨根問底，讓學生自由自在、靈活地思考，將學生的思維引向深入，拓展延伸，這樣，不僅能使學生深刻地掌握知識點， 還能使其舉一反三、觸類旁通，更有利于讓學生深刻理解知識的本質，合理、科學地構建知識結構體系。如案例：幾何綜合問題：如圖1，直線y=kx-2k（k<0）與y軸交于點A，與x軸交于點B，AB=2。

（1）求A，B兩點的坐標。

（2）如圖2，以AB為邊，在第一象限內畫出正方形ABCD，求直線CD的解析式。

（3）如圖3，在（2）的基礎上，正方形ABCD的對角線AC、BD交于點G，函數y=ax（a>0）和y=mx+n（m<0）的圖象經過點G，請利用這兩個函數的圖像，直接寫出當當ax>mx+n時，x的取值范圍。

學生很容易發現，第（3）題是函數圖像的交點問題，要求出x的取值范圍，關鍵是求出G的坐標，因此學生很快想到利用知道兩點求出AC、BD所在直線的函數的方法解決問題。

教師追問：除了這種方法去解決這個問題外，還有其他的方法嗎？

（學生作圖并思考。）

生1：過點G分別作GH⊥A0、GP⊥A0、先證明△AGH≌△BGP，再證明正方形OPGH，就可以求出G點的坐標。

生2：也可以利用一元一次方程求出G點的坐標。

師：為什么可以這樣，說出你的理由。

生2：剛才那位同學已證明了△AGH≌△BGP，得出AH=BP。設AH=BP=x，即4-x=2+x，求出x的值，命題得證。

師：很巧妙的方法！這是運用了代數方法解決的幾何問題。

師：可還有其他辦法？

一下子，學生思維瞬間得到激化，主動參與，積極思考和解決問題，課堂展現了最精彩的瞬間。很多學生在問題（3）的解決上也想到了幾何方法。

由此可見，有效的追問是引領學生深入探索的鑰匙以及促進學生能力提升的利器，因此，教師應準確把握追問的時機并圍繞知識核心進行智慧追問，以幫助學生拓展思維的空間與深度。

三、化解危機進行有效追問

數學課堂中隨時有“意外”發生，這就需要教師機智靈活地把握那些稍縱即逝的課堂契機，捕捉生成信息，巧妙地追問，把課堂中的“意外”巧妙地引導到有價值的思維軌道上來，促進學生積極思考，主動探索，形成知識的動態生成，實現“有效學習”。

總之，在核心素養下，“有效追問”在初中數學課堂中的作用是非常重要的。老師采取有效追問，既能提高學生的積極性和促使思維的發展，使數學課堂不再無趣，又能提高數學課堂的質量，提高學生的創新思維能力，使我們的數學課堂充滿活力。