勾股定理四步曲

肖友文

摘要：本文就北師大版八年級數(shù)學上冊第一單元《勾股定理》的教學，結(jié)合學生的學習情況提出了自己的四個方面的教學意見，目的是為了更有效地實施有效教學，進一步激發(fā)學生的學習興趣與熱情，充分地發(fā)揮勾股定理在教學實踐中的多種功能.

關(guān)鍵詞：講故事、找鋪墊、重歸納、巧設(shè)計、數(shù)學思想方法滲透

勾股定理是幾何學中的明珠，之所以它充滿魅力，是因為千百年來人們對它的證明趨之若騖，其中有著名的數(shù)學家，也有業(yè)余數(shù)學愛好者，有普通的老百姓，也有尊貴的政要權(quán)貴，甚至有國家總統(tǒng).北師大版八年級數(shù)學上冊第一單元就是學習勾股定理，作為教師如何引導好學生認真順利地學習有關(guān)勾股定理的知識并加以應(yīng)用，下面就如何實施與開以展教學談自己的幾點思考.

一、講故事，激發(fā)學生的學習興趣

課前我就與勾股定理有關(guān)的故事作一些比較全面的互聯(lián)網(wǎng)搜索，并進一步進行整理，旨在通過讓學生自己來講故事的形式使他們能更加具體、全面、深刻地了解勾股定理的由來，并激發(fā)大家對數(shù)學知識的求知欲望與強烈的興趣愛好.

二、找鋪墊，理清新舊知識的聯(lián)系

在學習勾股定理之前，我試著與學生一起重溫以下兩個方面的知識，目的是讓學生在后面的學習中能更加順理成章，這也符合建構(gòu)主義的理論，簡單地說來就是任何新知識的獲得，都要建立在新舊知識的聯(lián)系上，不能脫節(jié).

1.復習以前學過的直角三角形的有關(guān)知識

①什么叫做直角三角形？答：有一個角是直角的三角形叫做直角三角形;

②直角三角形中三個角有什么關(guān)系？答：三個角的和是180°，兩個銳角互余;

③直角三角形三條邊有什么大小關(guān)系？答：有三邊關(guān)系定理，任意兩邊之和大于第三邊;

④有哪些特殊的直角三角形？答：有等腰直角三角形，還有30°、60°的直角三角形.

2.1-20的平方的運算

平方雖然是乘法的特殊情形，但它卻是四則運算之外的對于學生來講比較陌生的一種運算，其中的原因是學生對平方的概念理解不透，所以造成運算的錯誤，具體又分三種類型的題目來做.

①計算1-20的平方;

②反過來做這樣的填空題，=25，=64等等;

說明：這里面很多學生都會想到，因為有前面的1-20的平方計算做基礎(chǔ)，但是存在的問題是幾乎所有的學生都漏了相對應(yīng)的負數(shù)，也就是忽略了互為相反數(shù)的兩個數(shù)的平方是相等的這個性質(zhì)，所以也可以幫助學生復習鞏固一下，順便也可為后一單元學習數(shù)的平方根打下基礎(chǔ).

三、重歸納，提高學生的解題能力

題型的歸類有助于幫助學生提高思維的條理性與清晰度，幫助學生系統(tǒng)地掌握好應(yīng)該掌握的知識，并進一步形成自己的知識網(wǎng)絡(luò)，最終達到形成自己的基本技能.勾股定理的有關(guān)題目大致上可以分為以下三種：

1.直接用勾股定理計算

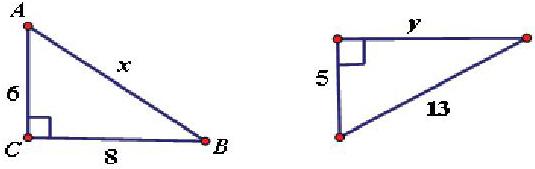
例1：求下列直角三角形中未知邊的長度.

分析：象這種題目一定要讓學生先觀察圖形，找出直角邊與斜邊，然后利用公式寫出直角邊的平方和等于斜邊的平方，即有，從而計算出結(jié)果.

2.缺圖形

例2：在Rt△ABC中，∠C=90°，AC=6，BC=8，求AB的長.

分析：這一題沒有圖形，要求學生根據(jù)題目的意思畫出圖形來然后列式進行計算，把圖形畫出來，就知道與例題1中的第一個圖是一樣的，所以象這種題目其實是加了一個對數(shù)學語言的理解并把它轉(zhuǎn)化成圖形.

對應(yīng)練習：

①、在△ABC中，∠C=90°，若 a=5，b=12，則 c=___________;

②、在△ABC中，∠C=90°，若c=10，a∶ b=3∶4，則SRt△ABC=____________;

③、等腰△ABC的腰長AB=10cm，底BC為16cm，則底邊上的高為 ，面積為 .

3.需要設(shè)未知數(shù)列方程來解決

例3：一個直角三角形的斜邊為20cm，且兩直角邊的長度比為3∶4，求兩直角邊的長.

分析：未知的有兩直角邊，也就是說有兩個未知數(shù)，所以要根據(jù)比為3∶4設(shè)兩直角邊分別為3xcm和4xcm，然后用勾股定理列式進行解方程來求解.

解： 設(shè)兩直角邊分別為3xcm和4xcm，

由勾股定理得，

求得，所以兩直角邊分別為6cm和8cm.

對應(yīng)練習：一直角三角形的三邊分別為a、b、c，其中a=3，b=4，求c的長.

說明：這一題不但考查學生通過讀題得出圖形的能力，還要求學生注意題目中的細節(jié)問題，就是題中沒有說明c是不是斜邊，所以要分兩種情況來解答.

四、巧設(shè)計，滲透數(shù)學思想方法

日本數(shù)學家和數(shù)學教育家米山國藏曾經(jīng)說過這樣一段話：學生在中學階段所學的數(shù)學知識，在進入社會后，幾乎沒有什么機會應(yīng)用，因而作為知識的數(shù)學，通常在出校門不到一兩年就忘掉了，然而不管他們從事什么業(yè)務(wù)工作，那種銘刻于頭腦中的數(shù)學精神和數(shù)學思想方法，卻長期地在他們的生活和工作中發(fā)揮著重要的作用。是啊，要讓學生的頭腦充滿理性思考，那數(shù)學課堂教學的支點在哪里呢？經(jīng)驗是數(shù)學的基礎(chǔ)，問題是數(shù)學的心臟，思考是數(shù)學的核心，發(fā)展是數(shù)學的目標，思想方法是數(shù)學的靈魂，勾股定理這一單元里面蘊含著豐富的數(shù)學思想方法，只要我們在課堂巧妙地進行設(shè)計，于無形中去滲透，方能達到教學的最終的目標.

五、結(jié)束語

在教學中我就是按照這樣的思路去實施教學，可以說收到了自己意想不到的效果，下面是我教的班里面的部分學生的學習體會：現(xiàn)在我們已經(jīng)學習了勾股定理，也知道了勾股定理就是說在一個直角三角形中三條邊存在一個關(guān)系：兩直角邊的平方和等于斜邊的平方，公式就是.用這個定理可以來進行計算，求出直角三角形中未知的一邊來，看起來這么簡單的一個定理，里面去蘊藏著豐富的故事與數(shù)學道理.所以通過這次不同一般的數(shù)學課活動，讓我們認識到了原來數(shù)學課并不是我們以前所想象的那樣，只有老師的講解與同學們的模仿與練習，而是可以有一些那么有趣的活動，比如自己來說故事;還有勾股定理的證明方法讓我們也學到了一些令人驚嘆的技巧，比如那些數(shù)與形結(jié)合的思想，讓我們感受到數(shù)與形結(jié)合得那么美妙，這些不僅激發(fā)了我們濃厚的學習興趣與熱情，還鍛煉了我們的意志與提高了利用網(wǎng)絡(luò)資源的技能，可謂受益匪淺.