航天器自適應有限時間反步控制

(浙江工業大學 信息工程學院，浙江 杭州 310023)

在編隊飛行、衛星通信和太空站對接等諸多航天任務中，航天器姿態跟蹤控制是任務成功的關鍵因素。航天器在軌運行時，往往存在著內部轉動慣量不確定以及外部未知擾動等不確定因素的影響，為保證航天器的姿態跟蹤性能，提出了許多非線性控制方法，包括滑模控制[1]、自適應控制[2]、反步控制[3]、逆最優控制[4]和H∞控制[5]等。其中，反步控制方法[6-7]是一種基于Lyapunov定理的遞歸設計方法，易于控制器設計，因此在航天器領域被廣泛應用[8-9]。然而，傳統反步法需要不斷對虛擬控制律求導而導致復雜性爆炸問題，針對這一問題有研究者提出動態面方法[10]，然而該方法并未考慮虛擬控制律通過濾波器以后產生的誤差補償問題。近來，Farrell等[11]提出一種命令濾波方法，在解決復雜性爆炸問題的同時，設計誤差補償信號彌補動態面方法的不足。然而，該方法設計的控制器只能保證系統狀態在無窮時間內達到漸進穩定。與漸近穩定控制相比，有限時間控制能夠保證系統狀態的有限時間穩定，具有較快的收斂速度、較高的控制精度和較好的魯棒性等特性，因此已被廣泛應用于航天器控制中[12-14]。王輝等[15]結合反步法和滑模控制設計有限時間控制器，然而由于虛擬控制律指數項的作用，其導數可能會引起奇異值問題。馬廣富等[16]針對組合體航天器的姿態控制問題，提出基于命令濾波的有限時間控制方法，但其濾波器本身并不能保證有限時間收斂。Yu等[17]提出一種有限時間命令濾波反步控制方法實現系統狀態的有限時間控制，然而其系統模型需要完全已知。

筆者針對慣量矩陣不確定和外部干擾的航天器姿態跟蹤問題，建立基于四元數描述的系統模型；設計有限時間濾波器逼近虛擬控制律的導數，從而避免可能出現的奇異值問題；設計神經網絡用于估計系統的不確定函數，并結合命令濾波反步法設計有限時間姿態跟蹤控制器，從而保證系統的跟蹤誤差能在有限時間內收斂到零點附近；最后，給出數值仿真驗證筆者所提方法的有效性。

1 問題描述

考慮由四元數描述的航天器運動學和動力學方程[18]，即

(1)

(2)

(3)

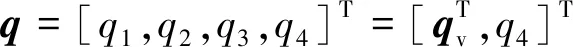
(4)

期望的姿態運動方程可以描述[19]為

(5)

(6)

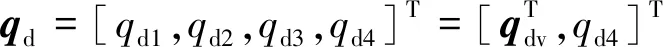
考慮由四元數描述的航天器相對運動姿態，即

(7)

(8)

ωe=ω-Cωd

(9)

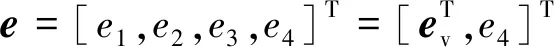
(10)

(11)

(12)

令J=J0+ΔJ,J0為轉動慣量的已知標稱值，ΔJ為轉動慣量有界的不確定部分。將J=J0+ΔJ代入式(12)可得

(13)

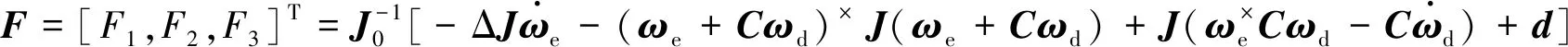
根據式(10)和式(13)，姿態跟蹤誤差模型可以重寫為

(14)

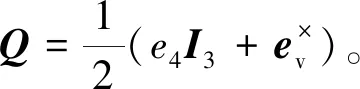
本研究的控制目標針對帶有慣量矩陣不確定和外部干擾的航天器系統式(10～12)，設計有限時間控制器，使得跟蹤誤差ev和ωe可以在有限時間內收斂到零點附近的小鄰域內。

2 有限時間反步控制設計

2.1 有限時間命令濾波器

有限時間命令濾波器定義[20]為

(15)

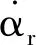
引理1[20]在輸入沒有噪聲的情況下，等式在有限時間內成立，即

(16)

當輸入受噪聲影響時，假設輸入噪聲滿足|αr-αr0|≤κ，其中αr0為實際信號，則在有限時間內，不等式成立，即

|φ1-αr0|≤ζ1κ=?1

(17)

(18)

式中ζ1,ζ2為兩個正常數。

2.2 神經網絡

針對非線性系統中的未知函數f(Z)，可設計神經網絡進行估計，即

fnn(Z)=WTΦ(Z)

(19)

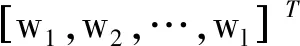
(20)

引理2[21]如果有在緊集Ωz上連續的函數f(Z)，對于任何給定的精確度標準ε>0，則存在神經網絡W*TΦ(Z)，當節點數l足夠多時有

f(Z)=W*TΦ(Z)+ε

(21)

式中W*為理想權值矢量，具體定義為

(22)

2.3 控制器設計

定義虛擬狀態量

(23)

式中ωc為以下有限時間命令濾波器輸出，即

(24)

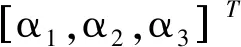
定義濾波誤差補償信號為ξ1和ξ2，然后令s1=z1-ξ1，s2=z2-ξ2。

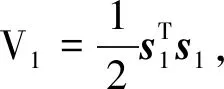
(25)

設計虛擬控制函數α和補償信號ξ1為

α=Q-1[-k1z1-λ1sigγ(s1)]

(26)

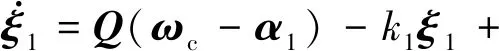
(27)

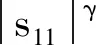
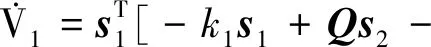
(28)

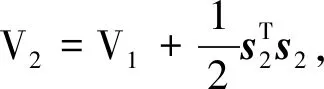
(29)

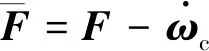
(30)

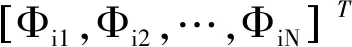
設計控制函數u和補償信號ξ2為

(31)

(32)

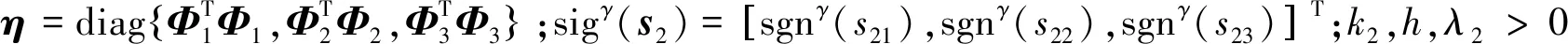
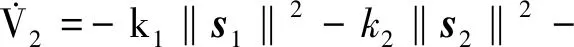
(33)

根據楊氏不等式，不等式成立，即

(34)

(35)

(36)

將式(34～36)代入式(33)，可得

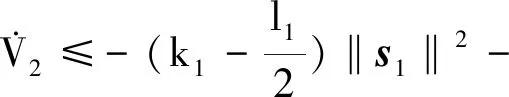
步驟3選取Lyapunov函數

(38)

并對其求導可得

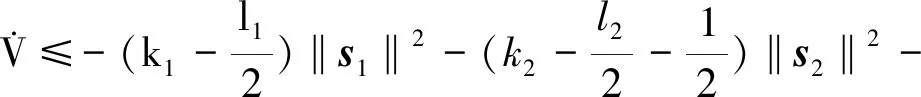
(39)

設計自適應更新律為

(40)

式中τ,m>0為設計參數。

3 穩定性證明

在穩定性證明之前，首先給出有限時間引理。

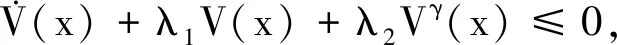
(41)

式中V(0)是V(x)的初始值。

定理1針對航天器系統式(10～12)，設計限時間命令濾波器式(24)，虛擬控制律式(26)，實際控制律式(31)，補償函數式(27)、式(32)和自適應更新律式(40)，則航天器姿態跟蹤誤差能夠在有限時間內收斂到零點附近的小鄰域內。

證明將自適應更新律式(40)代入式(39)，可得

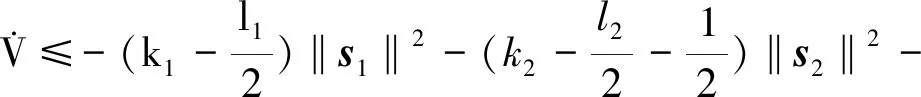
(42)

由楊氏不等式可知

(43)

由于0<γ<1，可得

(44)

將式(43，44)代入式(42)，可得

(45)

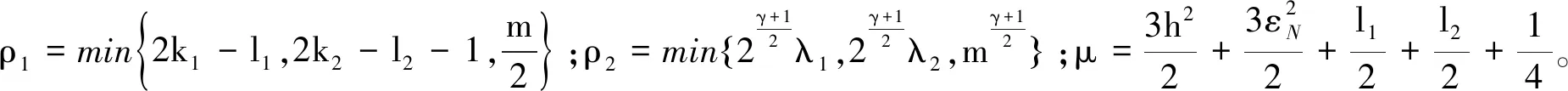
由于s1=z1-ξ1和s2=z2-ξ2，若能保證ξ1和ξ2在有限時間內收斂，則虛擬狀態量z1和z2將在有限時間收斂到零點附近的鄰域內。

因此，設計Lyapunov函數為

(46)

對式(46)求導，可得

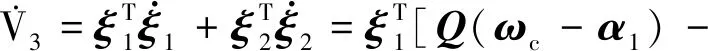
(47)

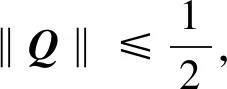
(48)

將式(48)代入式(47)，可得

(49)

根據式(49)和引理3可得，選取適當參數l1,l2，ξ1和ξ2將在有限時間T3收斂到零點。因此，虛擬變量z1和z2可以在有限時間T=T1+T2+T3收斂到零點附近鄰域內。根據定義式(23)可知，航天器狀態能夠在有限時間內跟蹤期望軌跡。證畢。

4 數值仿真

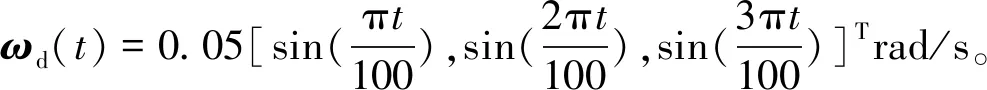
ΔJ=diag{sin(0.1t),2sin(0.2t),
3sin(0.3t)} kg·m2

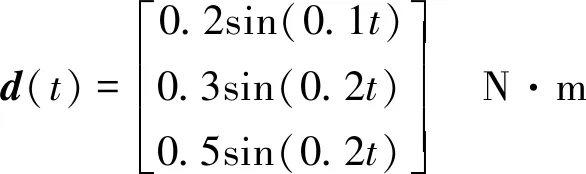
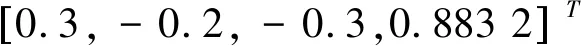
為了體現筆者提出控制方法的優越性，將對兩種控制方法進行對比仿真：

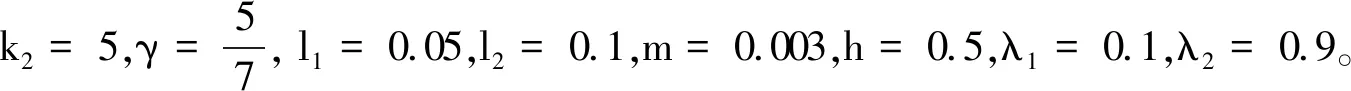
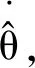
ωc=-k1Q-1z1

(50)

(51)

(52)

控制器相關參數選取均與M1方法相同。

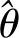
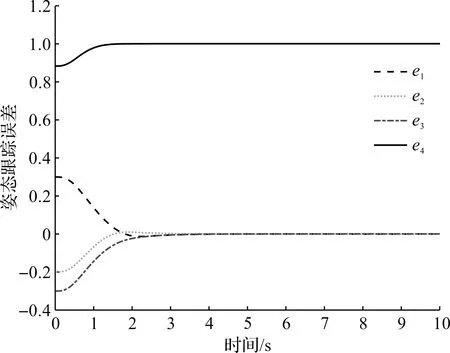
圖1 M1四元數跟蹤誤差eFig.1 M1 quaternion tracking errors e

圖2 M2四元數跟蹤誤差eFig.2 M2 quaternion tracking errors e

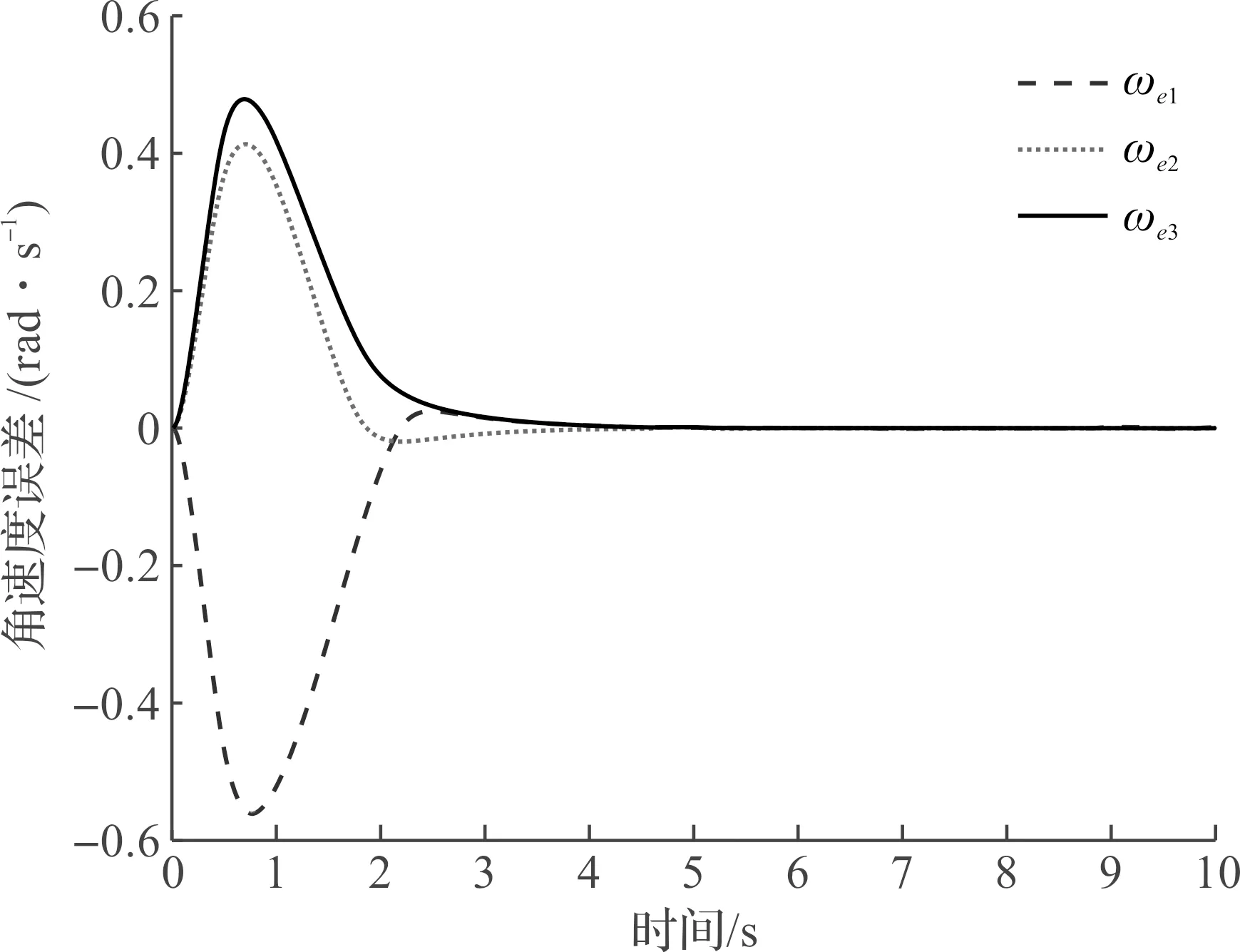
圖3 M1角速度跟蹤誤差ωeFig.3 M1 angular velocity tracking errors ωe

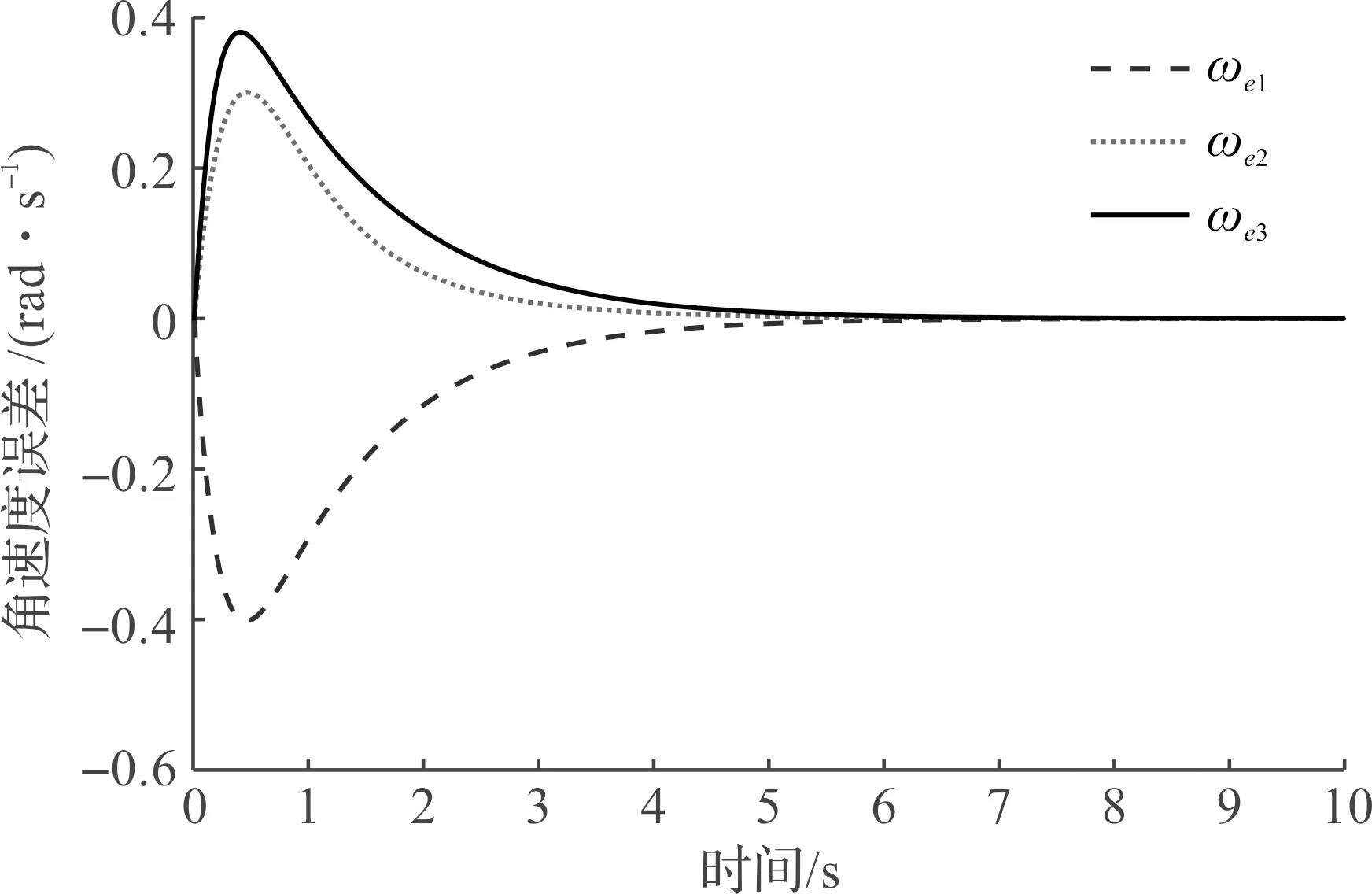
圖4 M2角速度跟蹤誤差ωeFig.4 M2 angular velocity tracking errors ωe

圖5 M1控制力矩uFig.5 M1 control torque u

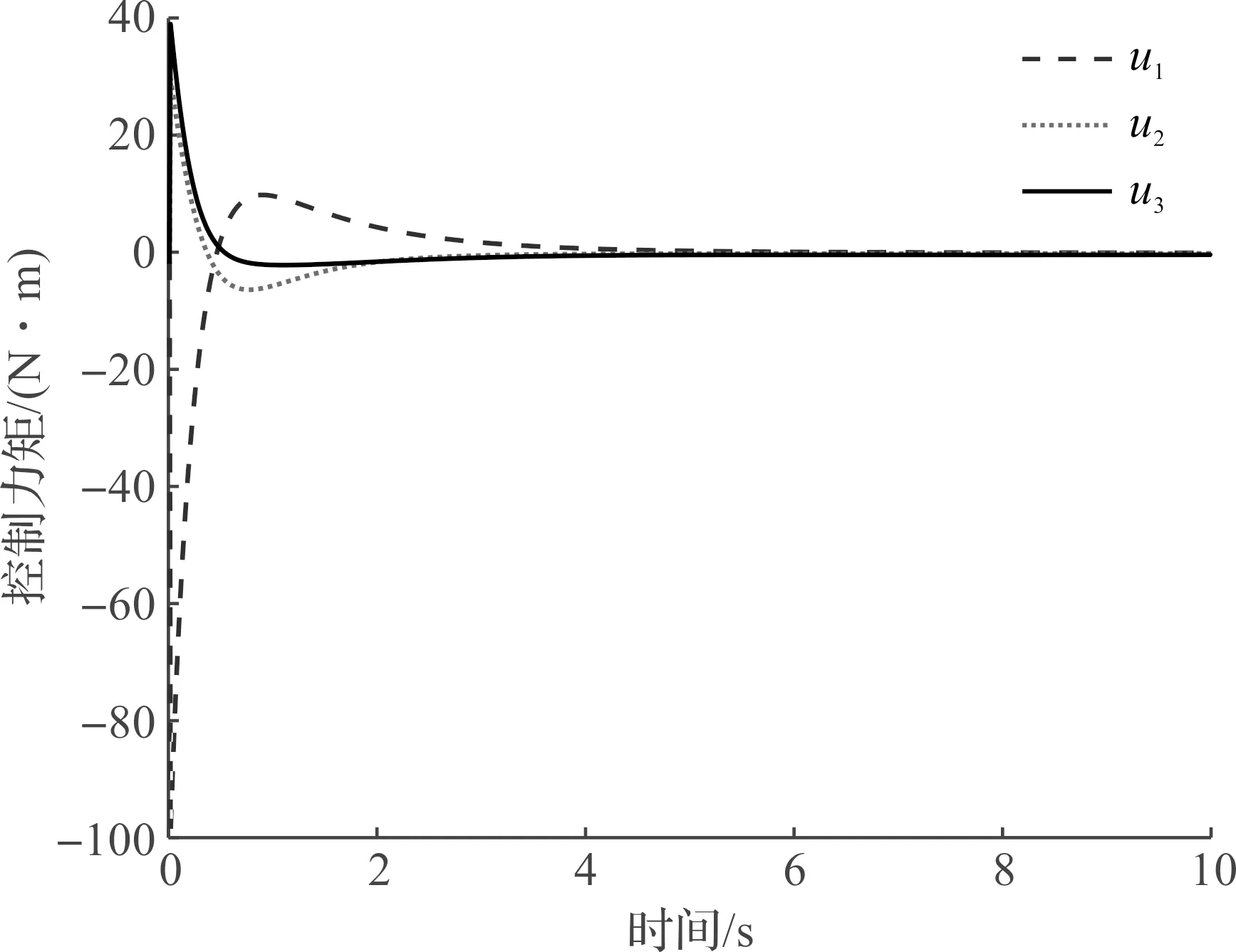
圖6 M2控制力矩uFig.6 M2 control torque u

圖7 M1虛擬狀態量z1Fig.7 M1 virtual state z1

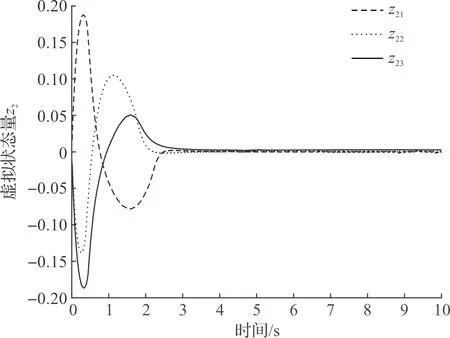
圖8 M1虛擬狀態量z2Fig.8 M1 virtual state z2

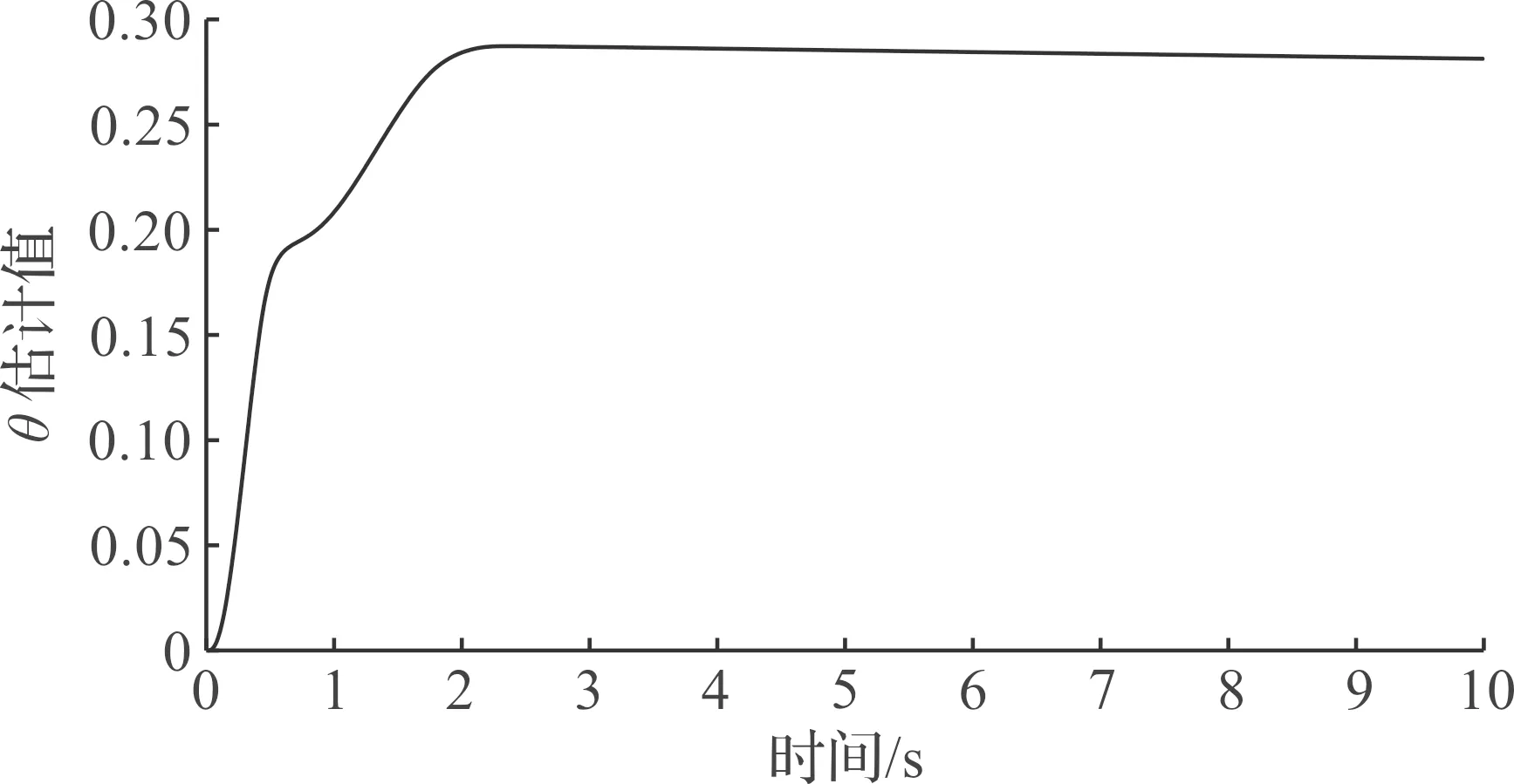
圖9 M1估計參數Fig.9 M1 estimated parameter

5 結 論

針對帶有轉動慣量不確定和外部干擾的航天器，筆者建立基于四元數描述的姿態跟蹤模型，并提出自適應有限時間反步控制方法。設計有限時間命令濾波估計虛擬控制律導數，進而避免奇異值問題。同時采用神經網絡估計未知非線性函數，并通過給出穩定性分析，證明所設計控制器能夠保證跟蹤誤差能夠在有限時間內收斂。仿真結果驗證了筆者方法的有效性。