基于ARIMA-GRNN組合模型的汽車零部件需求預測研究

耿立校，張永杰（河北工業大學 經濟管理學院，天津 300130）

0 引言

迄今為止，汽車零部件企業進行需求預測主要還是以傳統的時間序列預測為主，其中自回歸移動平均模型（ARIMA）就是當中最具代表性的時間序列預測法，該模型可以對任何數據建立時間序列進行分析和預測[1]，因此ARIMA模型被廣泛應用于股價預測、人口預測、流行疾病預測、企業需求預測等[2]。由于市場具有很大的波動性從而導致時間序列具有大量非線性特征，傳統時間序列預測法在處理線性時間序列擁有獨特的優勢，但是無法解釋時間序列中非線性時間序列信息。伴隨人工智能的發展與興起使得各種先進算法被大量的使用在非線性數據處理，先進算法處理非線性數據可以極大提升預測精度。國內學者胡寧靜和陳宏針對網絡流量的時變形和非線性指出運用單一的預測方法較難精準預測網絡流量[3]。另外，彭連會和張祥波構建ARIMA-RBF組合模型充分利用ARIMA的先進擬合算法功能與RBF非線性擬合算法功能，對重慶市月度降雨量進行實際預測，結果表明ARIMA-RBF組合預測模型是一種優越的算法[4]。

文章構建ARIMA-GRNN組合預測模型來精準處理時間序列集中的線性序列與非線性序列，并利用無錫博世公司CRIN3-18型號產品2016～2018年產品每月實際銷售數據進行仿真和測試，將兩種模型的預測結果進行比較，驗證組合預測模型精確度與可靠性。

1 背景知識

1.1ARIMA模型

ARIMA模型全稱差分自回歸移動平均模型，是將非平穩時間序列經過d階差分處理轉化為平穩時間序列，然后將因變量僅對它的滯后值以及隨機誤差的現值和滯后值進行回歸所建立的模型。

假設有一組樣本時間序列Zt｛｝弱平穩數據，經過d階差分處理轉化為：

所以ARIMA模型的可以表示為：

上式中：B是后移算子且BkZt=Zt-k；▽是差分符號且▽=1-B；t是第t時刻的時間點；Zt是第t時刻的時間序列值，βt是均值為0且方差為σa的白噪聲。

1.2 RBF神經網絡模型

RBF神經網絡是由一個具有徑向基函數神經元的隱層和一個具有線性神經元的輸出層構成的兩層向前神經網絡[5]。RBF函數神經元的傳遞函數最常用高斯函數作為神經元的傳遞函數，神經元radbas的輸入是向量p和權值向量w之間的距離與閥值b之間的乘積。泛化回歸神經網絡GRNN是由一個徑向基網絡層和一個特殊的線性網絡層0組成，常用于函數逼近[5]。

2ARIMA-BP組合模型構建

假設原始時間序列Zt｛｝由線性時間序列Pt｛｝和非線性時間序列Qt｛｝構成即：

ARIMA-BP組合模型預測步驟：

Step1：ARIMA模型對原始時間序列｛Zt｝進行預測結果為原始時間序列｝與預測時間序列之間的誤差假設為｛Dt｝，誤差序列｛Dt｝中則隱藏著原始時間序列｛Zt｝的非線性關系。式（4） 中F為非線性函數，ωt隨機誤差。

Step2：利用徑向基神經網絡強大的非線性函數逼近功能，對誤差序列｛Dt｝實現函數逼近。假設誤差序列｛Dt｝的預測序列為｛D't｝。

3 實例仿真

仿真數據來源于無錫博世公司CRIN3-18型號產品2016年1月至2018年12月每月實際銷售數據（仿真數據以作保密處理）如圖1所示。

3.1 ARIMA模型預測

2016年1月至2018年12月一共有36組原始時間序列可視化后如圖1所示。圖1顯示出3年內每個月產品需求量的波動較大，原始時間序列是非平穩時間序列需要利用差分處理使原始時間序列趨于平穩。原始時間序列1階差分處理后如圖2所示。

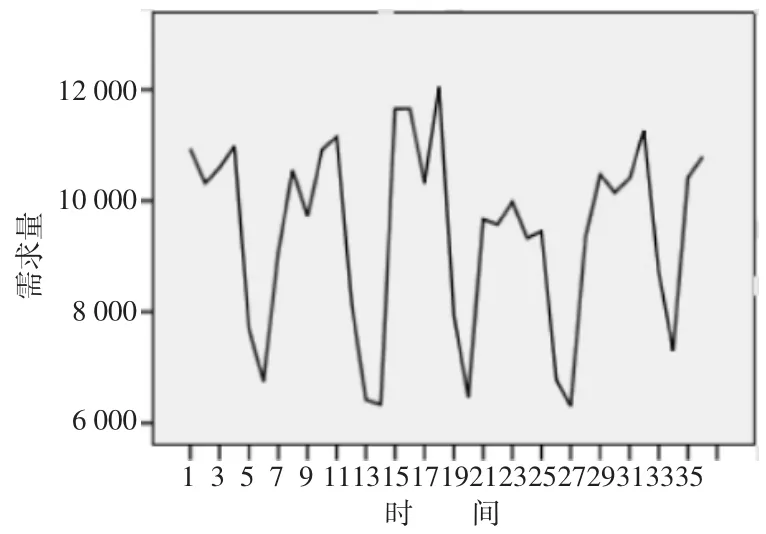
圖1 原始時間序列圖

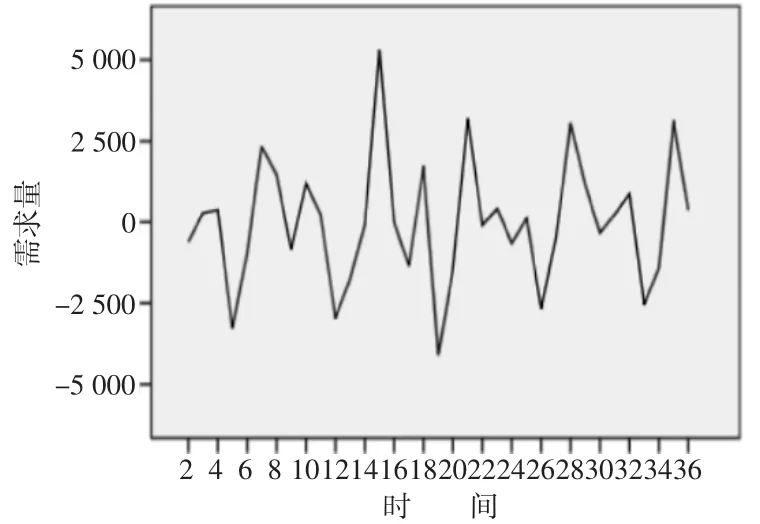
圖2 原始時間序列1階差分圖

原始時間序列經過1階差分處理均勻分布在0刻度線附近，可以視為差分后的時間序列趨于平穩所以d取值為1。1階差分時間序列的自相關和偏自相關圖如圖3和圖4所示，經過試驗對比p取8、q取1時AIC和BIC取得最小值分別為615.96和633.38。

Ljung-Box檢驗對殘差序列檢驗其Prob值均大于0.05，殘差序列不存在自相關性，而且QQ圖檢驗（如圖5）所示結果表明基本符合正態分布，最后對進行原始時間序列進行預測，如圖6所示。

3.2 GRNN神經網絡誤差值預測

由于ARIMA預測結果與實際值之間存在較大的誤差，根據第二步利用泛化回歸神經網絡（GRNN）進行對誤差序列實現函數逼近，仿真結果如圖7所示。

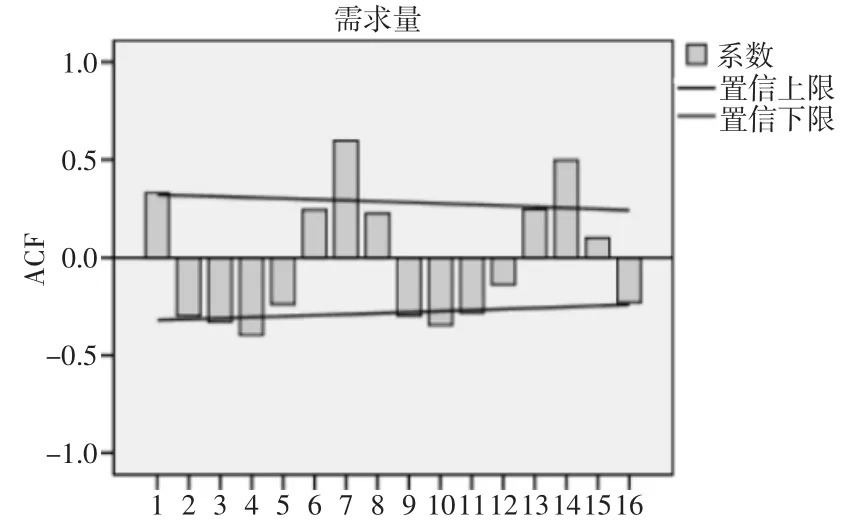
圖3 1階差分自相關圖

圖4 1階差分偏自相關圖

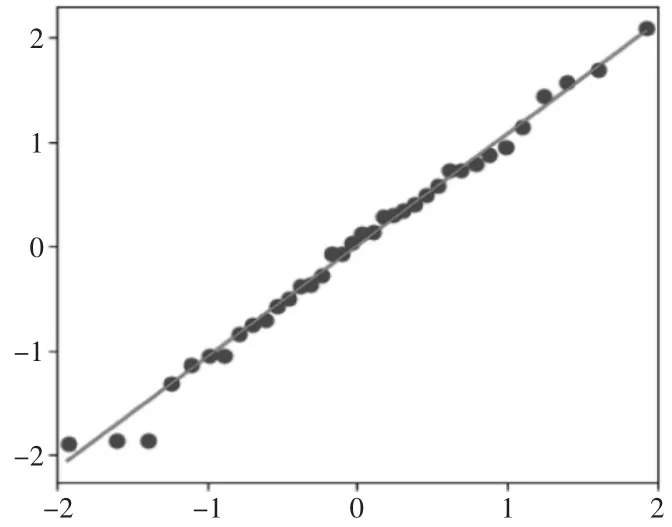
圖5 正態度分布檢測圖

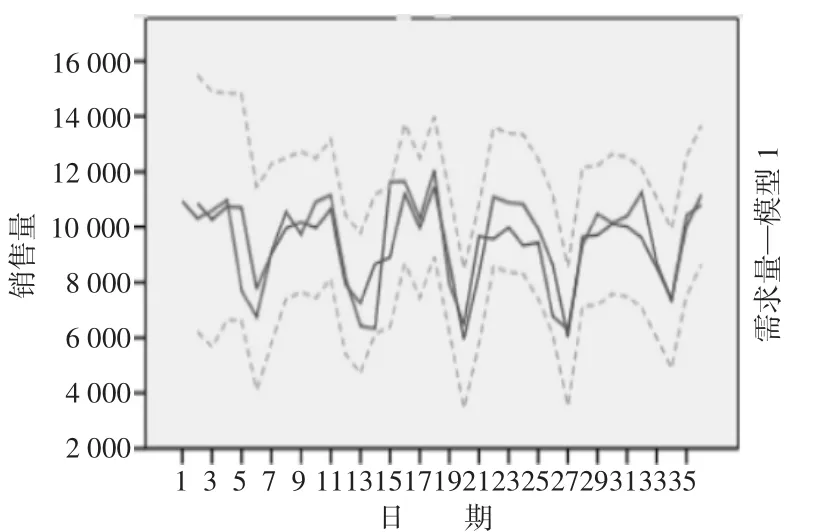
圖6 ARIMA（ 8,1, ）1模型預測結果

3.3ARIMA-GRNN組合模型預測

根據第三步將ARIMA（ 8,1,1 ）對原始時間序列預測值與GRNN神經網絡對誤差預測值相加的值就是ARIMA-GRNN組合模型的預測值，如圖8所示。

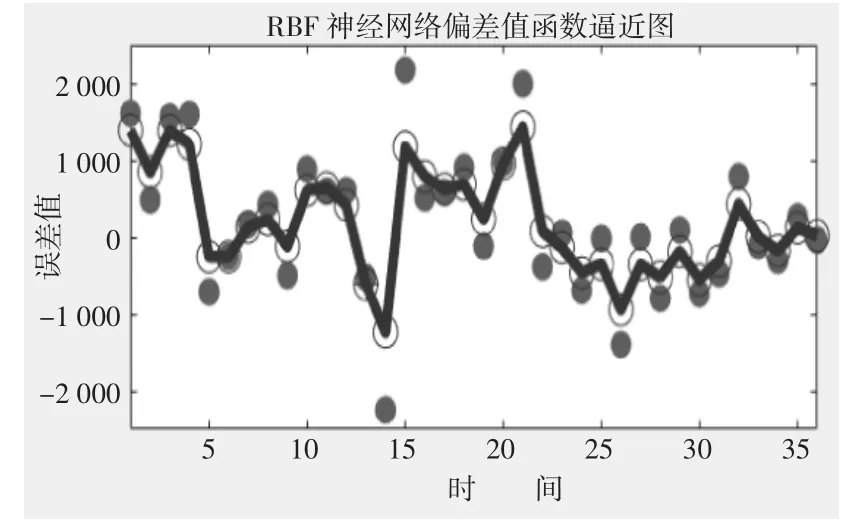
圖7 GRNN神經網絡誤差值函數逼近圖

圖8 ARIMA-GRNN組合模型預測圖

3.4 性能評估

最后通過RMSE和MAPE對兩種模型評價，其中ARIMA模型的均方根誤差值為0.093、平均絕對誤差值為7.771，ARIMA-GRNN組合模型均方根誤差值為0.036平均絕對誤差值為3.085。綜合上述：ARIMA-GRNN組合模型的預測精度明顯優于ARIMA模型，且預測結果科學可靠。

4 結束語

本文利用ARIMA模型處理線性數據和GRNN神經網絡處理非線性數據各自特點，將兩種模型進行組合充分發揮出兩者的優點。試驗表明ARIMA-GRNN組合模型的預測精度明顯優于單一模型，而且精確度更加科學可靠。對于在智能制造模式下幫助汽車零部件企業提高需求預測精度具有一定的幫助與提升意義。