考慮訂貨協調成本與數量折扣的改良品供應鏈水平協調

張云豐，王 勇，龔本剛，但 斌

(1. 安徽工程大學管理工程學院，安徽 蕪湖 241000；2. 重慶大學經濟與工商管理學院，重慶 400030)

1 引言

改良品(Ameliorating Items)是指在持有期間，隨著時間的推移，自身會發生數量增加、重量增長或質量改善，從而使得經濟價值或效用獲得提升的一類物品[1-2]。現實生活中有許多改良品的例子，如處于育肥期的生豬、快速生長的家禽、魚塘中飼養的魚、基地培植的水果蔬菜、酒莊里儲存的高檔酒類等都屬于改良品的范疇[3]。根據改良品在持有期間呈現出的不同改良特征，又可將改良品的改良現象分為有形改良和無形改良。有形改良是指在持有期間，由于生長或繁殖使得物品數量增加、重量增長而導致經濟價值或效用提升的一類改良現象；無形改良雖然在持有期間不會發生數量增加或重量增長，但其質量卻隨著時間的推移而得到明顯提升[4]。改良品在持有期間隨時間推移會發生改良現象，因此與其他物品相比較更具有特殊性。Wee等[5]認為少量的改良品訂貨可憑直覺或經驗完成而影響不大，對大規模的改良品訂貨問題，按照科學合理的方法進行是非常必要的。Chou等[6]指出改良品在存儲期的特點與易變質品正好相反，其訂貨問題值得進行深入研究。

然而，學者們對改良品訂貨問題的研究起步卻較晚。直到1997年，Hwang[1]才首次研究了改良品的庫存決策，在假設改良品的改良率服從兩參數威布爾分布的基礎上，建立改良品補貨模型。隨后，Hwang[7-8]、Modal等[2,9]、Law和Wee[10]、Wee等[5]、Chou等[6]、Goyal等[11]、Panda等[12]、Vandana和Srivastava[13]基于不同的假設條件，如考慮需求依賴價格、資金時間價值、通貨膨脹率、有限計劃期、斜坡型需求率等，分別探討了威布爾分布改良率的改良品庫存最優決策問題，而Moon等[3]、Sana[14]、Dem和Singh[15]、Mahata和De[16]則在考慮了時變需求、通貨膨脹、交易信用、資金時間價值等因素對庫存系統成本影響的基礎上，各自構建了常系數改良率下的改良品庫存控制模型。國內學者對改良品的研究才開始，著重從供應鏈協調的視角展開，如王勇等[17]、孫海雷等[18]、張云豐等[4,19]分別探討了常系數改良率下改良品供應鏈的協調機制。

改良品與其他物品的不同之處在于持有期間會發生改良現象，而改良率是描述改良現象的關鍵參數。上述文獻在改良率的處理上有兩種方式，一是假設改良率服從兩參數威布爾分布，另一種則將改良率設置為常系數。無論是何種處理方式，都未有實證數據予以支撐。陳暉等[20]以處于育肥期的生豬為研究對象，通過調研現場數據擬合育肥生豬的改良率曲線后發現，育肥生豬的改良率特征比較復雜，先是呈近似線性下降趨勢，接著類似于威布爾分布，后期下降到一個較小值且逐漸減小。銷售商庫存中的改良品已處于在售狀態，因而屬于改良末期階段。在欄生豬育肥是物品發生有形改良使得重量增加的典型案例，聯系到育肥生豬在育肥末期改良率的特征，可對處于銷售庫存系統中該類物品的改良率按常系數作近似處理。

供應鏈中的不同經濟主體在面臨決策時，通常會以自身利益最大化作為唯一目標，即使在實現該目標時可能會影響到其他主體或供應鏈整體的利益。雙重邊際效應的出現，使得整個供應鏈系統的利益受損，此時設計適當的協調機制來對供應鏈中的個體經濟行為加以協調則尤為必要。目前，學者們的研究興趣主要聚焦于供應鏈上下游節點企業間的垂直(縱向)協調，如生產商與銷售商決策行為的協調[21-26]。除此之外，在企業運作實踐中，供應鏈水平(橫向)協調也十分常見，如多個銷售商之間開展聯合補貨。通過實施聯合補貨，銷售商可以分攤訂貨成本，提高與上游供應商談判的話語權，容易爭取到更多的折扣價格優惠，最終有利于實現規模經濟。聯合補貨的局限性在于參與聯合補貨的銷售商需要改變自身原先的采購節奏，產生額外的訂貨協調成本，并且當較多的銷售商加入到聯合補貨組織時，會導致生產運作速度變慢，采購業務的效率大大降低。Zhang Jiawei[26]指出聯合補貨的訂貨協調成本通常會隨著采購組織中參與人員數量的增長而增加。張云豐等[28]設計了銷售商聯合補貨的協調成本函數，但文中尚存在兩點不足之處：一是所設計的訂貨協調成本函數中增加的協調成本與增長的銷售商數量是正比例關系，過于簡單；二是雖然考慮了持續補貨對改良品供應鏈系統成本的影響，卻在對銷售商成本函數作近似處理過程中忽略了補貨速率的影響。本文遵循張云豐等[28]的研究思路并進一步完善其研究，主要不同點在于：一是設計更為合理的訂貨協調成本函數；二是充分體現補貨速率對供應鏈系統成本的影響；三是提出基于博弈核心的利潤分配方法。

2 基本假設與符號說明

2.1 基本假設

本文建立的改良品供應鏈協調模型基于以下基本假設：

(1) 單個供應商和多個銷售商構成二級改良品供應鏈；(2) 只涉及一種改良品的訂貨決策；(3) 不允許銷售商缺貨；(4) 考慮無限個訂貨周期；(5) 提前期忽略不計；(6) 需求率已知且均勻穩定；(7) 供應商采用持續補充模式；(8) 改良率為常系數；(9) 持有期間改良的部分占有庫存；(10) 供應商提供等級折扣價格策略；(11) 每個銷售商獨立補貨時具有相同的訂貨成本。

2.2 符號說明

本文建立的改良品供應鏈協調模型設定如下符號：

Di：第i個銷售商的市場需求率，i=1,2,…,n；

R：供應商提供的統一補貨速率，R>Di；

K：銷售商獨立補貨時的訂貨成本；

KJ：銷售商聯合補貨時的訂貨成本，KJ>K；

Hi：第i個銷售商的單位存儲成本；

Ci：第i個銷售商的單位改良成本；

ωi：銷售商i獨立補貨時的單位批發價格，ωi>Ci；

ωJ：銷售商聯合補貨時的單位批發價格，ωJ>Ci；

p0：改良品在市場上的單位銷售價格；

λ：改良品的凈改良率；

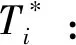
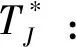
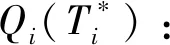
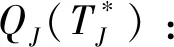
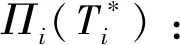
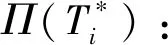
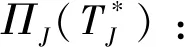
3 模型

3.1 獨立補貨模型

設第i個銷售商的一個補貨周期長度為Ti，從t=0時刻開始補貨，在補充、改良與需求的共同作用下，庫存逐漸增加，至t=ti時刻持有的庫存水平達到最大值；隨后供應商停止補貨，庫存在改良與需求的影響下慢慢減少，在t=Ti時刻達到最小值零。接著，第二輪補貨開始。第i個銷售商獨立補貨的模型圖如下圖1所示。

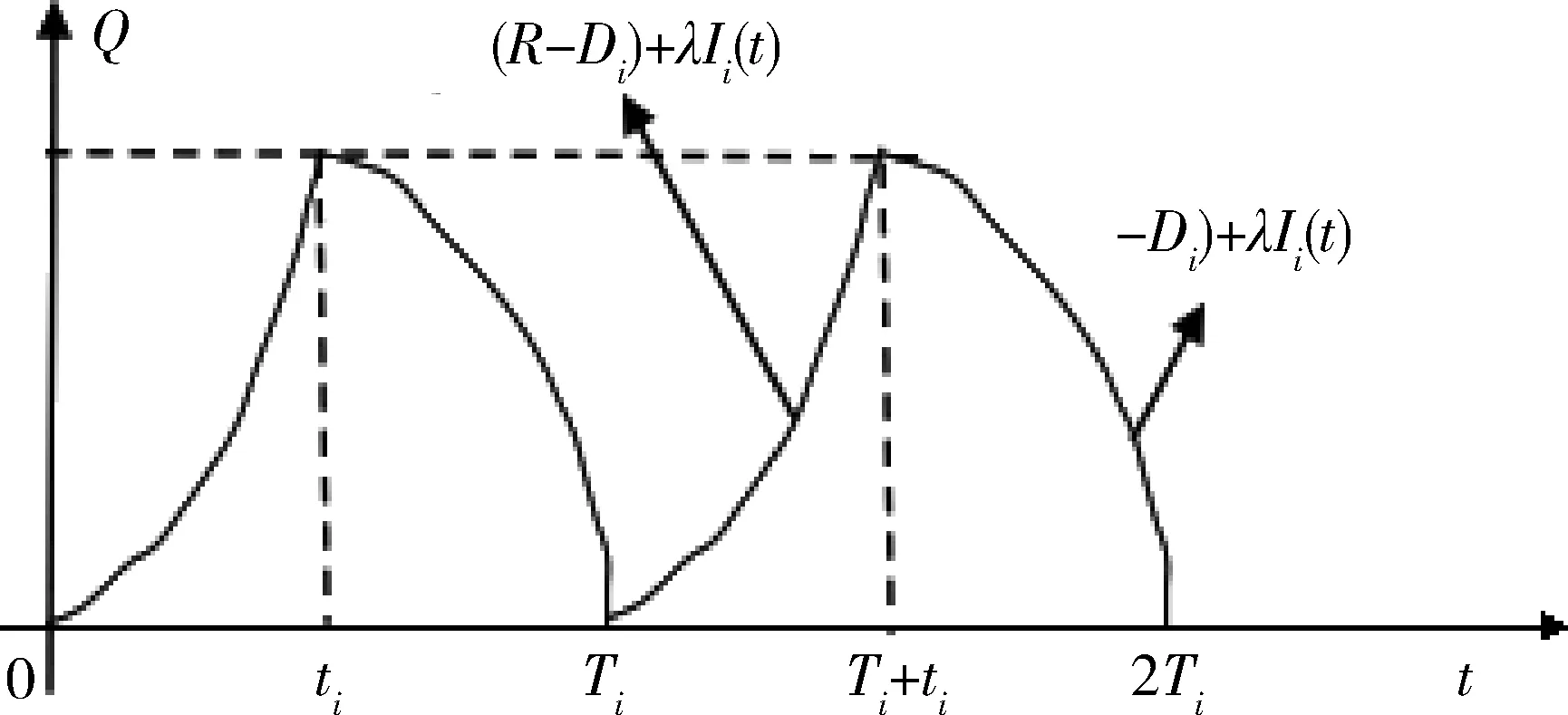
圖1 獨立補貨模型圖

第i個銷售商在一個補貨周期內任意時刻持有的庫存水平Ii(t)滿足微分方程

(1)

其中，n取自然數。

結合邊界條件Ii(0)=0與Ii(Ti)=0，運用常數變易法求解式(1)，得到

Ii(t)=

(2)

當t=(n-1)Ti+ti時，有(R-Di)(eλti-1)/λ=Di(1-eλ(ti-Ti))/λ成立。直接求解ti與Ti之間的表達式很困難，這里借鑒Sivashankari等[29]的處理方式，將式中的指數函數進行泰勒展開，并取其前兩項，得到ti=DiTi/R。

第i個銷售商在一個補貨周期Ti的總成本包括訂貨成本、采購成本、存儲成本、改良成本四個部分，分別為：

(1) 訂貨成本

=K；

(2) 采購成本

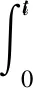
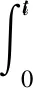
(3) 存儲成本

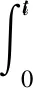
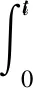
(4) 改良成本

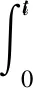
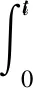
從而，第i個銷售商的單位時間利潤表達式為

(3)

命題1 第i個銷售商獨立補貨時的最佳訂貨周期與最大單位時間利潤分別為

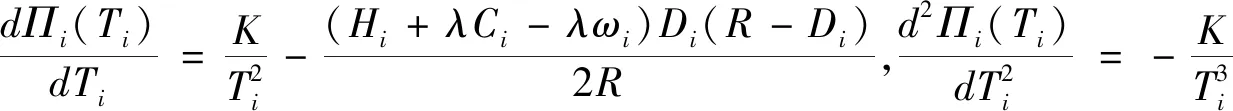
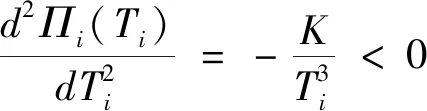
其中，Hi+λCi-λωi>0。

第i個銷售商的最優訂購數量為

(4)

當R→+∞，即供應商的補貨速率無窮大，便可得到瞬時補充下第i個銷售商的最佳補貨周期和最大單位時間利潤。此時有

將第i個銷售商在持續補充與瞬時補充下的最大單位時間利潤進行比較，有

因此，持續補貨能夠獲得比瞬時補貨更大的單位時間利潤。n個銷售商在獨立補貨下的最大單位時間總利潤為

(5)

3.2 聯合補貨模型

設n個銷售商組建采購聯盟N，共同決策補貨周期TJ。采購聯盟N需要協調每個銷售商的補貨計劃，并因此產生相應的訂貨協調成本。在此，假定采購聯盟N總的訂貨協調成本函數為KJ=Knφ，其中φ表示協調成本系數且φ>0，n表示采購聯盟中成員的數量。由dKJ/dn=φKnφ-1>0知隨著參與聯合補貨的銷售商數量增長，整個采購聯盟的訂貨協調成本也在增加。當d2KJ/dn2=φ(φ-1)Knφ-2<0時，即φ<1，表示任意銷售商加入到采購聯盟的邊際協調成本遞減；當d2KJ/dn2=φ(φ-1)Knφ-2>0時，即φ>1，表示任意銷售商加入到采購聯盟的邊際協調成本遞增；當d2KJ/dn2=φ(φ-1)Knφ-2=0時，即φ=1，表示任意銷售商加入到采購聯盟的邊際協調成本不變。

(6)

命題2 若n個銷售商聯合補貨，則采購聯盟N的最佳訂貨周期與最大單位時間總利潤分別為

證明：將式(6)對TJ分別求一階、二階導數，有

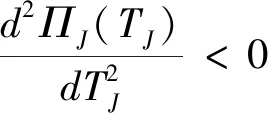
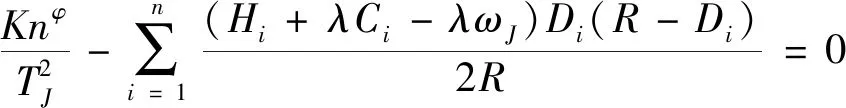
采購聯盟N的最優訂購數量為

(7)

當R→+∞，即供應商的補貨速率無窮大，便可得到瞬時補貨下采購聯盟N的最佳補貨周期和最大單位時間總利潤。此時有

聯合補貨時，采購聯盟N在持續補充與瞬時補充下的最大單位時間總利潤差值為

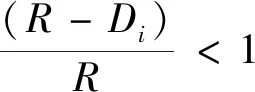
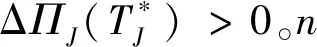
3.3 兩種補貨模式比較

(8)

在式(8)中，考慮聯合補貨模式下單位產品批發價格ωJ和協調成本系數φ對ΔΠ的影響。由于采購聯盟N在聯合補貨時的訂貨數量通常大于任一銷售商在獨立補貨時的訂貨數量。因此，在供應商提供數量折扣策略下一般有ωJ≤ωi成立。在聯合補貨時，采購聯盟N需要協調各個銷售商的行動，并產生相應的訂貨協調成本，所以聯合補貨會使得訂貨成本KJ大于獨立補貨時的訂貨成本K。協調成本系數φ反映了采購聯盟N在聯合補貨時的訂貨協調成本大小。如果協調成本系數φ較大，表示采購聯盟N對各個銷售商的協調變得比較困難，可能導致聯合補貨獲得的價格節約不足以補償訂貨協調成本的增加。為了確保聯合補貨優于獨立補貨，協調成本系數φ需滿足下列條件。

命題3 在由單個供應商和n個銷售商構成的二級改良品供應鏈中，聯合補貨優于獨立補貨的充要條件是協調成本系數φ需滿足

φ<

(9)

證明：當ΔΠ>0時，聯合補貨優于獨立補貨。由式(8)知應滿足

在供應商提供等級折扣價格時，式(9)中ωi/ωJ是訂貨數量的函數，需要通過試錯法來確定。設供應商提供的m等級折扣價格函數為

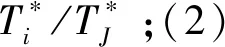
4 聯合補貨博弈

4.1 問題描述

雖然聯合補貨能獲得比獨立補貨更大的單位時間總利潤，但尚不足以保證所有的銷售商都會加入到采購聯盟N中來，除非每一位銷售商都能夠獲得不小于自己在獨立補貨下的單位時間利潤，如此才能讓每一位銷售商有動力參與聯合補貨，從而實現利潤的增加。

本文以聯合補貨的最大單位時間總利潤作為分配對象，將聯合補貨的利潤分配轉換成多人合作博弈的收益分配問題。以N={1,2,…,n}表示n個銷售商的集合，稱為全聯盟。函數Φ:2N→R為分派給任意非空子聯盟S?N的特征函數，且Φ(φ)=0，Φ(S)稱為聯合補貨博弈(N,Φ)中子聯盟S的最大單位時間總利潤。聯合補貨博弈需要解決的問題是在全聯盟成立后，如何將整個聯盟的最大單位時間總利潤Φ(N)合理分配給每位銷售商。

定義1 對任意的S?N，子聯盟S的利潤是最大化聯盟在聯合補貨時所產生的單位時間總利潤。改良品聯合補貨博弈(S,Φ)可定義為

(10)

其中，s表示子聯盟S中銷售商的數量，以此類推。

4.2 基本性質

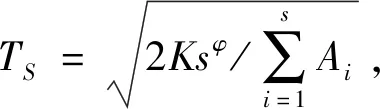
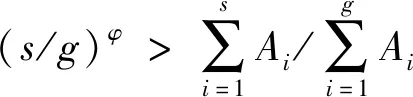
性質1表明，在聯合補貨博弈中，當協調成本系數滿足一定條件時，采購聯盟的規模越大，其補貨的最佳訂貨周期越短。因而每位銷售商持有的最大庫存量將減少，平均庫存水平也因此隨最佳訂貨周期的縮短而降低，使得單位時間承擔的庫存成本降低。因此，參加采購聯盟進行聯合補貨有利于每位銷售商提高企業利潤水平。

性質2 對任意的采購子聯盟S,G?N

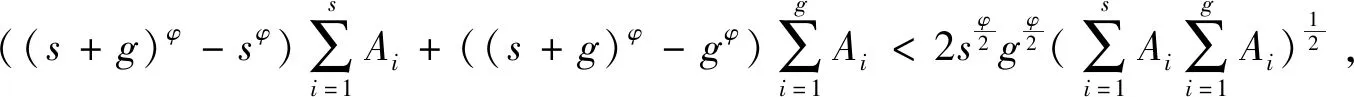
證明：

Φ(S∪G)-(Φ(S)+Φ(G))

顯然，若有

性質2表明，當協調成本系數滿足一定條件時，聯合補貨博弈(N,Φ)具有次可加性，合作是有益的。對各銷售商而言，聯合補貨的最大單位時間總利潤將大于獨立補貨的最大單位時間利潤之和。從理論上來說，只要采取合適的利潤分配方案就能夠使所有的銷售商實現利潤的帕累托改善。

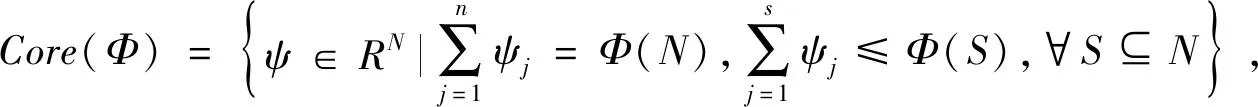
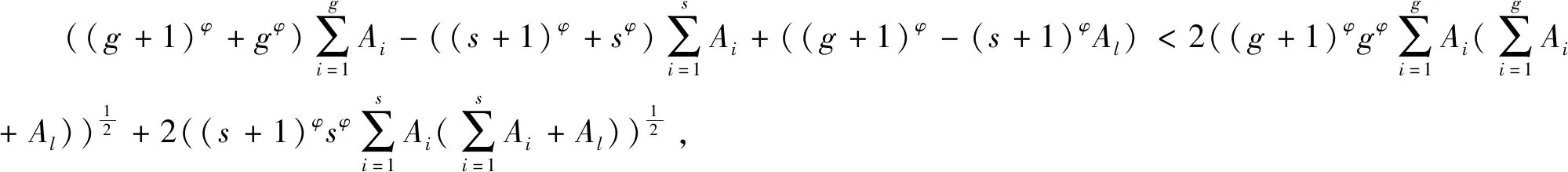
證明：對任意的S?G?N{l}，有

欲證Φ(G∪{l})-Φ(G)>Φ(S∪{l})-Φ(S)，即

對不等式兩邊平方并消去公因子2K，得到

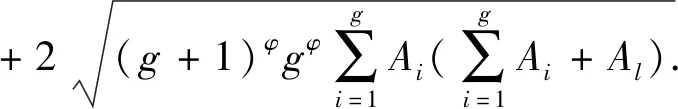
性質3表明，當協調成本系數滿足一定條件時，銷售商對所屬采購聯盟的邊際利潤隨著采購聯盟規模的增大而增大，任意一個銷售商或子聯盟加入另一個不相連子聯盟的動機隨著聯盟成員的增多而增大。所以，每位銷售商都有動機組建采購聯盟，并且傾向于加入成員較多的采購聯盟，這樣不僅能夠分攤訂貨成本，而且有可能由于訂貨批量的增大而享受更低的折扣價格，從而獲得更多的單位時間利潤。

4.3 利潤分配方案

子模博弈的核心非空且是其邊際向量的凸組合，夏普利值是核心的重心，然而核心是一個集合概念，并不是唯一的分配方案，且夏普利值的計算比較復雜，隨著聯盟參與人數的增加，其計算復雜度呈指數型增大[30]。因此，下文將設計一種屬于核心且易于計算的單值利潤分配方案。將全聯盟N的最大單位時間總利潤Φ(N)表示為

=Φ(S).

性質4表明，利潤分配方案ψ是一個公平且穩定的分配方案，這時沒有任何銷售商從全聯盟中撤出組建自己的聯盟，沒有任何子聯盟有動機從全聯盟中分離出來。

5 數值算例

5.1 參數設置與求解

在由單個供應商和三個銷售商組成的二級改良品供應鏈中，相關參數設置如下：D1=700千克/月，D2=800千克/月，D3=900千克/月，R=2000千克/月，H1=H2=H3=4.0元/千克·月，C1=C2=C3=12.0元/千克，K=200元，φ=0.5，λ=0.10，p0=25元/千克。供應商提供的等級折扣價格為：

ωJ(Q)

設三位銷售商組建采購聯盟N，共同決策訂貨周期，向改良品供應商進行聯合補貨，則N={1,2,3}，S可取{1}、{2}、{3}、{1,2}、{1,3}、{2,3}或{1,2,3}。將上述各項參數代入式(9)進行檢驗，易知當φ=0.5時，任意兩位及以上銷售商組建采購聯盟進行聯合補貨都比各自獨立補貨更優。對每一個子聯盟S，結合所設置的參數，得到下表1所示計算結果。

由表1數據可知，子聯盟的最佳訂貨周期隨著子聯盟規模的增大而逐漸減小，但子聯盟的最優訂貨批量卻隨著子聯盟規模的增大而逐漸增加。任意兩個及以上的銷售商聯合補貨所獲得的最大單位時間總利潤都會大于他們獨立補貨時的最大單位時間利潤之和。在現有的參數設計下，聯合采購優于獨立采購，并且采購聯盟的規模越大，聯合補貨的優勢越明顯。

表1 子聯盟訂貨參數

5.2 敏感性分析

下面分別考慮凈改良率λ、補貨速率R與協調成本系數φ發生變化時對各銷售商在獨立補貨與聯合補貨中最大單位時間利潤的影響，具體結果如表2-表4所示。

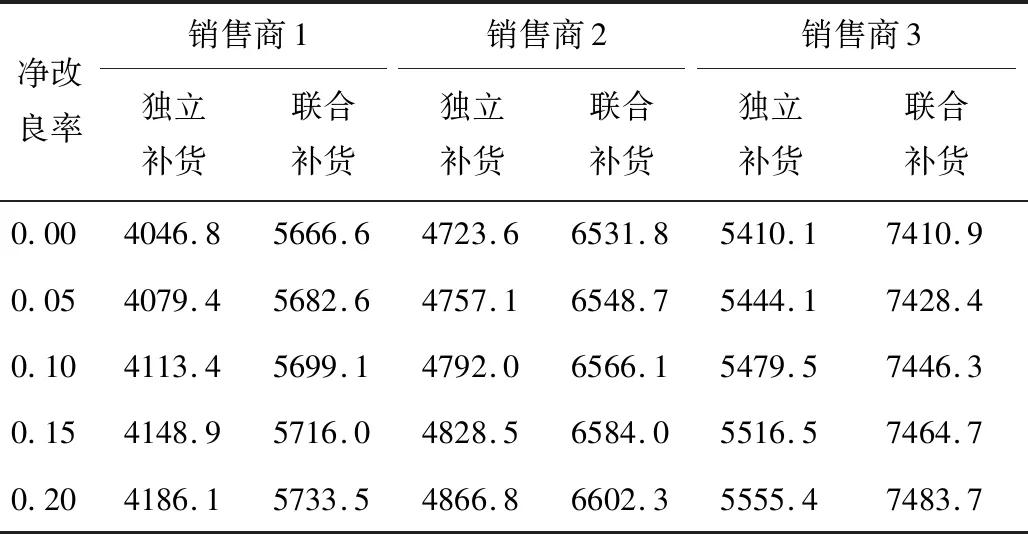
表2 凈改良率的敏感性分析

由表2數據可知，當單位改良成本小于批發價格時，無論是獨立補貨還是聯合補貨，三位銷售商的最大單位時間利潤都隨著凈改良率的增加而增加。此時，銷售商們更傾向于通過改良而不是直接采購來滿足需求。三位銷售商在聯合補貨中分配的最大單位時間利潤都明顯高于在獨立補貨下的最大單位時間利潤，主要原因來自于兩方面：一是在聯合補貨中每位銷售商分攤的訂貨協調成本比獨立補貨時小(獨立補貨下三位銷售商的總訂貨成本為600元，而在聯合補貨中三位銷售商的協調成本只有346.4元)；二是每位銷售商都享受到供應商提供的等級折扣價格，采購成本大幅度下降(每位銷售商獨立采購時的批發價格是18元/千克，聯合補貨時單次訂貨批量增加較多，從而享受到16元/千克的折扣價格，節約了采購成本)。最后，隨著改良率的增加，每位銷售商在聯合補貨與獨立補貨中獲得的最大單位時間利潤差值逐漸減小，這是由于聯合補貨的最佳訂貨周期比任何一位銷售商獨立補貨的最佳訂貨周期都短，因此持有期間改良品的改良量相對較少，而單位改良成本小于批發價格，所以聯合補貨在物品改良這部分增加的利潤比獨立補貨要少。

由表3數據可知，三位銷售商無論是采取獨立補貨還是聯合補貨，其獲得的最大單位時間利潤都隨著補貨速率的增加而減少。當補貨速率逐漸增加時，會導致最佳訂貨周期慢慢縮短，最優訂貨數量也在減少，周期平均存儲數量漸漸減少，如此使得單位時間的訂貨成本增加而單位時間的存儲成本減少，最終導致各位銷售商的最大單位時間利潤下降。在補貨速率增加的過程中，若剛好使得銷售商的最優訂貨數量下降到上一等級折扣價格對應的數量區間時，銷售商的最大單位時間利潤就會產生較大幅度的下降。極端情況下，若補貨速率趨向于無窮大，即瞬時補貨下，每位銷售商的最大單位時間利潤都下降到極小值。

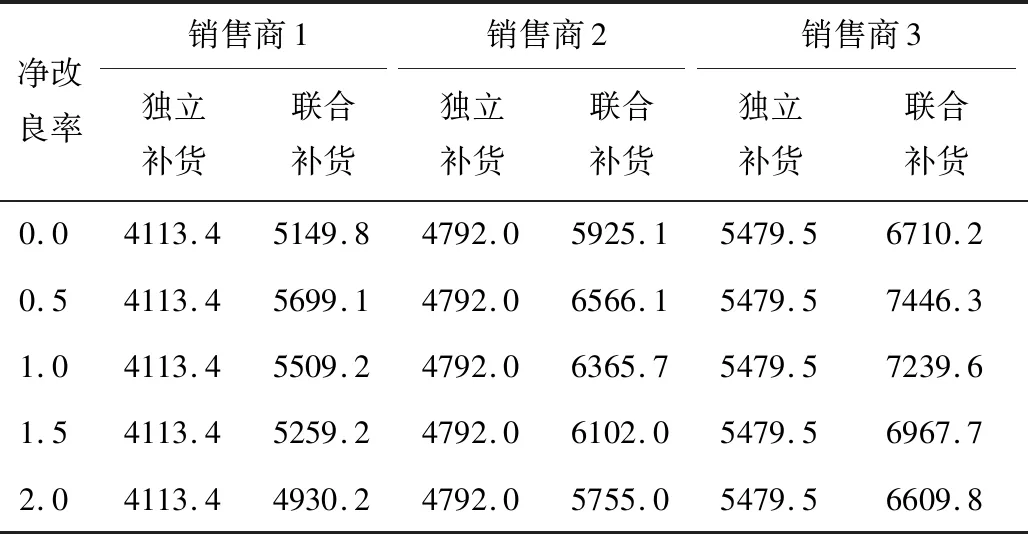
表4 協調成本系數的敏感性分析

由表4數據可知，協調成本系數的變化只對銷售商在聯合補貨下的最大單位時間利潤產生影響，而不會改變獨立補貨時的利潤水平。隨著協調成本系數的增加，三位銷售商在聯合補貨中分配的最大單位時間利潤不斷減少。可以預見的是，隨著協調成本系數的進一步增加，很快使得某位銷售商在聯合補貨中分配的最大單位時間利潤小于其在獨立補貨下的最大單位時間利潤，該銷售商會率先退出采購聯盟，并最終導致采購聯盟瓦解。根據命題3，可計算出本算例中協調成本系數的最大值maxφ≈2.98，即協調成本系數大于2.98時，三位銷售商在聯合補貨中獲得的最大單位時間總利潤將小于獨立補貨獲得的最大單位時間利潤之和，導致至少一位銷售商在加入采購聯盟后分配的利潤水平小于其獨立補貨。另外，表4數據表明，協調成本系數并非越小越好，如φ=0.0時各位銷售商分配的最大單位時間利潤就比φ=0.5時小。這是因為較小的協調成本系數對應著較小的最佳訂貨周期，意味著采購聯盟的最優訂貨數量較少，則有可能享受不到供應商提供的較為理想的折扣價格，從而導致銷售商的利潤水平大幅下降。

6 結語

本文的研究是對張云豐等[27]的完善和補充，討論了供應商提供持續補充方式與等級折扣價格下多銷售商的補貨決策問題，將銷售商在獨立補貨與聯合補貨兩種補貨模式的最大單位時間利潤進行了比較。文中考慮了組建采購聯盟進行聯合補貨時存在協調成本的影響，設計接近企業運作實際的協調成本函數。在得到聯合補貨優于獨立補貨充要條件的基礎上，將銷售商之間的聯合補貨行為轉化成多人合作博弈問題，證明博弈具有的基本性質，設計基于博弈核心的利潤分配方法。最后通過一個數值算例對文中給出的相關結論進行驗證。

論文證明聯合補貨博弈所具有的幾條基本性質是以協調成本系數滿足特定條件為前提的。本文研究結論的實踐意義在于，當組建采購聯盟進行聯合補貨的協調成本小于特定值時，銷售商們聯合補貨要優于獨立補貨，并且采購聯盟的規模越大，每位銷售商能夠從聯合補貨中獲得的單位時間利潤就越大。

文中在推導供應商的周期補充時間與銷售商的訂貨周期之間的函數關系時，借鑒了Sivashankari等[28]的處理方式，將指數函數進行泰勒展開并只取其前兩項。這是一種簡單的處理方式。這種做法與泰勒展開時取前三項相比存在一定的誤差，但在凈改良率與訂貨周期較小時(如取λ=0.10、T=0.5，相對誤差為0.12%)，所產生的誤差可以忽略不計。