數學史融入數學課堂教學的策略研究

孫麗娜

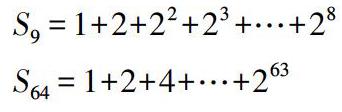
【摘要】近年來，越來越多的教師意識到數學史在數學教學中的重要性，體會到數學史的價值.教師擁有廣博的數學知識，在教學實踐中有效地將數學史融入數學課堂教學的情境創設、知識進程以及知識應用中，將課講活講透，使課堂教學更加生動、更具感染力，激發學生對數學學習的向往和探索，培養學生的創新思維.

【關鍵詞】數學史;課堂教學;策略

法國偉大的數學家亨利·龐加萊曾說：“如果我們想要預測數學的未來，那么適當的途徑是研究這門學科的歷史和現狀.”近幾年來，我國的數學教育改革中強調數學的文化價值，致使數學史得到廣泛的關注.數學教師在教學中，應積極主動、有意識地把數學史與數學教育進行有機結合.文章探討了將數學史融入數學課堂教學的策略，以激發學生學習數學的熱情，培養學生的數學素養.

一、數學課堂教學融入數學史的意義

數學是一門重要的基礎性學科，學好數學對其他理科科目的學習具有奠基作用.對于中學生來說，學好數學是很重要的事情.作為中學教師，要努力在課堂教學中吸引學生學習數學的興趣，提高課堂教學效率，而在中學數學課堂教學中有目的地融入數學文化、數學史內容不失為一種有效的方法.數學史和數學教學的有效融合，可以幫助學生更好地理解數學，提高對數學的宏觀認識，提高多元化的文化關懷以及人文素養.

1.提升學生的學習興趣和人文素養

隨著中學數學學習的不斷深入，學生需要掌握更多的數學知識.掌握這些數學知識，若只是靠單純地背誦定理公式，重復地進行習題練習，學生無法真正理解、掌握知識，甚至會失去學習數學的興趣.而在數學課堂中有效融入數學史、數學文化，使學生了解知識點的來歷，深入數學的本質，看到知識點背后的故事，學習數學名家們不畏艱難、不斷探索的精神，從而提高學生學習數學的興趣、主動性，提高對數學的宏觀認識，提升人文素養.

2.提高學生的核心素養與實踐能力

數學教學的目的是教會學生應用，能利用所學的數學知識解決生活中的數學問題.教師將數學史融入數學課堂，同時充實多學科知識，加強數學和其他學科知識間的相互滲透與溝通，拉近數學與實際生活之間的距離，幫助學生在數學視角下發現、分析問題，從更廣泛、跨界的背景中觀察對象，形成更加全面而深刻的認知與見解;通過數學學科與其他學科的融合，學生會運用數學的眼光和思維發現問題，分析問題，解決問題，提高學生的核心素養與實踐能力.

二、數學史融入課堂教學的策略

1.數學史融入情境創設，激發學生對學習的向往

根據多年的教學實踐，一些有趣鮮活的數學故事能讓學生產生極高的興趣.因此結合教學內容，適當地利用數學史創設情境，創造出引人入勝的數學課堂，無論是對學生智力因素的發展或是非智力因素的成長，還是對課堂教學的豐富都起到積極的作用.將學生引入一個個數學猜想、一段段數學故事中，能夠激發學生對數學學習的向往和探索.

比如，教師在進行“等比數列求和”這一內容的教學時，可以創設以下兩個數學史情境：

情境1 用多媒體展示一首數學詩：

遠望巍巍塔九層，紅燈點點倍加增.

頂層閃爍燈一盞，試問共有幾盞燈？（注釋：燈由上往下依次倍增）

情境2 棋盤問題：

國王要獎賞國際象棋的發明者，問他想要什么.發明者說：“陛下，請您在這張棋盤的第一個小格內賞給我一粒麥子，在第二個小格內給兩粒，第三格內給四粒，依次類推，每個格子里放的麥粒數都是前一個格子里放的麥粒數的2倍，直到第64個格子為止.把這些擺滿棋盤上所有64格的麥粒都賞給您的仆人吧.”國王覺得這并不是很難辦到的事，就欣然同意了他的要求.國王應該給發明者多少粒麥粒呢？你認為國王有能力滿足發明者的要求嗎？

對于兩個情境的問題，學生很容易得出式子：

S9=1+2+22+23+…+28

S64=1+2+4+…+263

教師提問：如何求？

學生動手試著計算，他們會想到用計算器依次算出各項的值，再求和.我對他們的這種思路給予肯定.計算時學生會發現S9還好求，但是用計算器求S64卻很困難.

在實際教學中，受課堂時間限制，教師舍不得花時間讓學生去做所謂的“無用功”，急急忙忙地拋出“錯位相減法”，這樣做有悖學生的認知規律：求和就想到相加，這是合乎邏輯順理成章的事.因而教師在教學中應舍得花時間營造知識形成過程的氛圍，讓學生的思維從問題開始形成繁難的情境，激起學生的求知欲，迫使學生急于尋求解決問題的新方法，激發學生對數學學習的向往和探索，為后面的教學埋下伏筆.

2.數學史融入知識進程，激發學生積極探索

數學家發現數學的時候，是火熱地思考著的.一旦研究完畢，呈現在我們面前的則是冰冷的美麗形式.數學教師的任務不僅是把教材上的東西說清楚，還要對數學發展的來龍去脈有清楚的認識.數學學科對于學生而言是枯燥、乏味的，學生常常埋沒于做題，受迫于應試，逐漸失去了對數學學科的興趣.怎樣調動學生學習數學的積極性就成了一個迫切需要解決的問題.經過實踐教學，教師把數學史融入學生學習知識的進程中，將能夠體現知識系統產生、發展的數學史資料融入課堂教學中，能夠讓學生了解當時的數學家為什么和如何研究數學.引導學生了解知識產生的現實背景與問題背景，重溫知識系統產生、發展的歷史進程，可以幫助學生確立學習目標，積極探索，優化已有的認知，提升識別能力、創造能力.同時能讓學生受到數學思想的熏陶，讓學生在汲取數學知識原汁的過程中掌握、提煉數學方法，在數學知識這座寶殿中深刻理解數學的本質，并因此獲得數學能力與素養的提升，這才能真正說明學生已經成為知識的主人.

比如，初等數學中的起源，無理數的導入，確立圓周率，勾股定理，笛卡爾對直角坐標系的貢獻等，高等數學中的微積分的概念，函數的概念，非歐幾何的創立，不僅史料豐富，而且內容精彩，非常適合課堂教學，對學生理解所學的知識有很大的幫助.數學家發明、發現的生動過程，不僅可以使學生在抽象的數學學習中頓生趣味與親近感，還有助于學生理解這些數學概念、數學知識，對所學知識進行抽象和概括，在學習中學會反思， 將數學知識重新建構后融入自己的知識體系中.同時，對數學家的好奇與敬佩之情可以促進學生的積極探索、動手實踐、合作交流、自主閱讀，實現學習方式和思維模式的轉變.

3.數學史融入知識應用，培養學生創新思維

現在的數學教材中已經出現了很多數學史的內容，但是數學史的內容很多，教材中直接給出的只是其中很少一部分，還有一些數學史的內容是蘊含于數學知識中的，是可以從數學內容中反映出來的.如果教師擁有廣博的數學知識，就可以把顯性數學知識中所隱含的隱性數學文化及時挖掘出來，使數學知識與數學發展史相輔相成，達到有機統一.

例：（1）已知兩個定點A（-2，0），B（4，0），若動點P滿足 PA PB = 1 2 ，則點P的軌跡是;

（2）已知點M與橢圓 x2 169 + y2 144 =1的左焦點和右焦點的距離之比為2∶3，則點M的軌跡方程為.

教師在教學時注意不要浮于教材的表面，完全按照課本組織教學，就題論題，而是適時地引入阿波羅尼斯圓的文化背景，介紹古希臘著名的數學家阿波羅尼斯的生平事跡及他的經典巨著《圓錐曲線論》，在這部經典巨著中記載的一個著名的幾何問題：“在平面上給定相異兩點A，B，設P點在同一平面上，且滿足 PA PB =λ，當λ>0且λ≠1時，P點的軌跡是圓，這個圓我們稱作阿波羅尼斯圓.” 引導學生發現上面兩題的結論，動點的軌跡都是圓.數學史的學習激發了學生的學習興趣、探究欲望，最后得到一般性的推導.教師挖掘隱藏在知識背后的文化背景，使學生掌握的不僅是兩道看似孤立的習題，而是看到了這兩道題的文化背景，了解了知識是怎樣來的，也知道了知識應該怎樣應用，觸類旁通，不但激發了學生對古代數學家的敬仰之情，也提高了學生學習數學的興趣 ，更激發了學生創新的熱情，學生學習積極性高漲，教師教學效果顯著.

三、數學史融入課堂教學的原則

1.科學性

教師向學生傳授的數學史知識必須是正確的，我們應該尊重歷史，尊重事實，既不可隨意編造，也不能無端拔高，更不可藝術加工，把數學史當作故事隨意虛構.特別在講授中國的數學史時，實事求是，更能激發學生的民族自尊心和愛國主義熱情.

2.實用性與趣味性

教師所講的數學史，對學生的數學學習及將來的工作有直接幫助，要選取史料豐富、內容精彩的數學史內容應用于課堂教學，與知識性、實用性與趣味性共生，應避免照本宣科或嘩眾取寵，要寓教于樂，以教為本.這樣對學生理解所學的知識才有很大的幫助.

3.廣泛性

教師選取的數學史知識要不分年代，數學是幾千年來，全人類孜孜以求不斷探索，歷經千辛萬苦共同取得的財富，在整個數學科學的發展長河中，數學是在人類社會變革推動之下，各國數學家相互交流學習共同探索的結果，因此，在進行數學教學時，應注意選擇不同時期、不同國度的使用，這樣才能全面地、真正地、準確地展示數學史的全貌.

一位優秀的教師，不僅要授人以業，還要授人以法，進而授人以道，教師要掌握這些法和道必須宏觀地厘清數學發展的脈絡，深入數學的本質，對于數學創新來說，數學史研究更具有指引作用.數學史中記載了許多數學家發明、發現的生動過程，向學生介紹這些過程有助于學生理解，掌握創造的方法、技巧，從而增強其創造力.

總之，把數學史注入高中數學課堂教學，是對現階段教師提出的嚴峻要求.新的數學課程標準也增加了有關數學史方面的知識內容.學生在了解相關數學史內容的基礎上，應認識數學產生和發展的規律以及與社會發展的關系，不斷形成該階段應具備的數學思維和數學素養，自主構建數學知識體系.因此，數學教師必須不斷豐富自身的數學史知識，與相關數學知識融合，形成知識體系，并將其適時、恰當地應用于數學課堂教學中，為數學課堂教學服務，實現有效教學.

【參考文獻】

[1]張奠宙，王善平.數學文化教程[M].北京：高等教育出版社，2012（10）.

[2]王振輝，汪曉勤.數學史如何融入中學數學教材[J].數學通報，2003（9）.

[3]伏春玲，馮秀芳，董建德.數學文化在中學數學教學中的滲透 [J].數學教育學報，2012（6）.