把“提出問題”融入“變式教學”之中

石振興

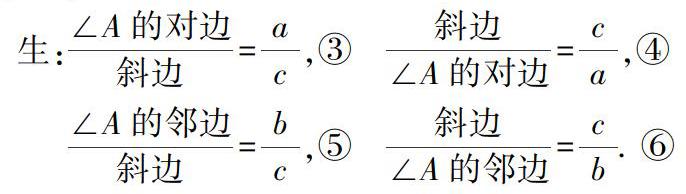
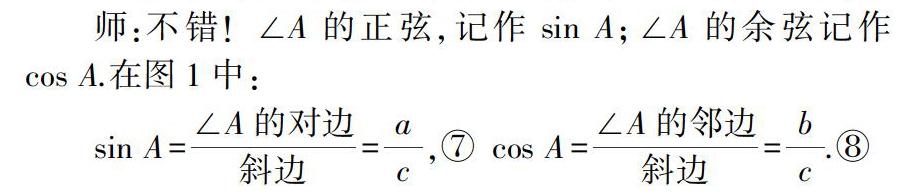
【摘要】《義務教育數學課程標準》指出：“數學教學活動應激發學生的興趣，調動學生的積極性，引導學生的數學思考，鼓勵學生的創造性思維.”同時，課程目標中也明確提出：“數學教學要培養學生的數學思維和提出問題、分析問題以及解決問題的能力”.“變式教學”應運而生，它是目標達成的重要方法.而傳統的教學中，教師只重視數學知識的“變式”和數學解題的“變式”，而忽視了問題發現和提出的創新.因此，在實際教學過程中，教師把“發現問題、提出問題”有效地融入“變式教學”中，不僅能夠有效地調動學會參與數學學習，更能激發學生的學習積極性，而且還可以培養學生的創新意識、創新思維和創新能力，使“教師為主導、學生為主體”的教學理念真正扎根發芽.

【關鍵詞】提出問題;變式教學;數學課標;數學思維

一、課前分析

創新來源于問題的提出和生成，沒有問題，創新就無從談起.長期以來，我們的中學數學課堂往往只關注問題的解決，卻忽視了其中更為重要的問題提出的教學，致使學生只會機械地做“答”，不會創造地提“問”.愛因斯坦說過：“提出一個問題往往比解決一個問題更重要.”因此，在實際教學中，我們不僅要重視問題解決過程中的創新，更要關注問題生成過程中的創新，把數學問題提出的訓練和強化作為今后數學創新教學的“契合點”.本文是冀教版初中數學九年級“正弦和余弦”一課的教學實錄，教學中突出對學生提出問題、生成問題的強化訓練和培養，引導學生養成自然而然、承上啟下的提出問題的習慣，強調問題的生成和升華，而不是單純地為了問而“提問題”.

二、教學案例

（一）回顧舊知，鞏固提升

師：在上一節課，我們學習了正切和余切.如圖1，請指出∠A的正切和余切分別是什么？（意在通過復習正切和余切引發問題）

（生思考、回憶正切和余切的定義）

生：tan A= ∠A的對邊[]∠A的鄰邊 = a[]b ，①

cot A=? ∠A的鄰邊 ∠A的對邊 = b a .②

（二）借助舊知，提出問題

師：我們通過學習，知道一個銳角的正切和余切是兩條直角邊的比值.那么，觀察圖1，你還有哪些發現？有什么問題可以提出來我們共同思考、分析.（教師可以適時進行啟發、引導）

（學生思考之后，舉手發言）

生：圖1中Rt△ABC的三條邊，除了兩條直角邊的比以外，還能組成其他的比，比如 ∠A的對邊 斜邊 ，除此以外，還能得到哪些比呢？

（學生從一個極其自然、樸素的角度提出了這么好的問題，很自然地就導入到本節課所要學習的內容，這充分說明，并不像有些教師說的那樣，學生不會提問題，更提不出什么有價值的問題.而是在很多時候，教師根本沒有給學生創造提問題的情境和機會，只是簡單地替代學生完成而已）

師：這個問題提得很好！有深度、有創意！那么，你還能組成哪些比呢？

生： ∠A的對邊 斜邊 = a c ，③? 斜邊 ∠A的對邊 = c a ，④

∠A的鄰邊 斜邊 = b c ，⑤

斜邊 ∠A的鄰邊 = c b . ⑥

（三）問題導入，引出課題

師：很好！上面的④和⑥分別叫作∠A的余割和正割.到高中以后會進行學習，我們初中階段暫時不做研究，但是你仍然很了不起，發現了我們今天要學習的兩種“新”的三角函數：正弦和余弦.

教師板書課題：正弦和余弦.

（四）歸納概括，總結定義

師：結合上節課的學習，誰能仿照∠A的正切和余切那樣，概括出∠A的正弦和余弦的定義？

生：如圖1，我們把∠A的對邊與斜邊的比叫作∠A的正弦;把∠A的鄰邊與斜邊的比叫作∠A的余弦.

（學生通過歸納、交流，概括出∠A的正弦和余弦的定義，其間可能會遇到些許問題，教師不要急于求成，替代學生，而應留給學生足夠的時間和空間，讓學生自主完成，這也是對學生進行抽象概括能力的訓練和培養的過程）

師：我們知道，∠A的正切和余切可以用其英文tangent和cotangent中的前三個字母來表示.那么，同學們你們認為∠A的正弦和余弦應當怎樣表示呢？同樣用正弦和余弦的英文sine和cosine中前三個字母來表示，可以嗎？（可以查閱英漢詞典）

（這個環節可以讓學生體會到知識間的相互聯系，培養學生凡事要問為什么、學習要刨根問底的良好習慣，同時培養學生的質疑能力及發現問題、解決問題的能力，從而推動學生不斷成長，促進其數學素養和綜合素質的有效提升.）

師：不錯！∠A的正弦，記作sin A;∠A的余弦記作cos A.在圖1中：

sin A= ∠A的對邊 斜邊 = a c ，⑦

cos A= ∠A的鄰邊 斜邊 = b c .⑧

（五）設計問題，揭示規律

師：剛才，我們學習了∠A的正弦和余弦.那么，誰能結合上節課所學的∠A的正切和余切的相關知識，設計幾個類似的問題？下面以組為單位，大家共同思考、交流，設計出一個問題，看哪個小組設計的問題最有代表性.

（教師深入到各小組，及時了解其具體進度，對有困難的小組給予引導：可以仿照正切和余切中的問題進行設計，如確定另一個銳角∠B的正弦、余弦;特殊角的正弦值、余弦值等，但最好能設計出創新性的問題：如∠A的正弦、余弦、正切、余切之間的關系.這個環節的設置可以讓學生學會用類比的方法設計問題，進一步培養和提升學生提出問題的能力）

小組1：在圖1中，請表示∠B的正弦和余弦.

（學生在弄清了正弦和余弦的定義的實質的基礎上，結合上節課所學的正切和余切，能夠提出相應的變式練習，這是非常難能可貴的，說明學生不僅掌握了所學知識，更掌握了探究問題的方法，教師應大力表揚）

師：思路很好！誰能結合圖1中的Rt△ABC，確定出∠B的正弦和余弦值？

生：sin B= ∠B的對邊 斜邊 = b c ，⑨

cos B= ∠B的鄰邊 斜邊 = a c .⑩

師：比較⑦⑧⑨⑩四個式子，同學們有沒有新的發現？

生：sin A=cos B，cos A=sin B.

師：在上面的兩個式子中，能否只用∠A來表示？

生：因為∠A+∠B=90°，所以∠B=90°-∠A，因此

sin A=cos（90°-∠A），cos A=sin （90°-∠A）.

師：對于任意的一個銳角，是否都具有上面的性質呢？若是，你能用語言文字敘述其性質嗎？

生：任意一個銳角的正弦值都等于它的余角的余弦值;任意一個銳角的余弦值都等于它的余角的正弦值.

師：你的敘述很準確，也很完整，表現真不錯！

小組2：如何求特殊角30°，45°，60°角的正弦值和余弦值？

師：很好！那么你們組求出這些角的正弦值和余弦值了嗎？

生：求出來了：

sin 30°= 1 2 ，sin 45°=? 2? 2 ，sin 60°=? 3? 2

cos 30°=? 3? 2 ，cos 45°=? 2? 2 ，cos 60°= 1 2 .

師：誰能代表你們組來闡述一下你們是如何求值的？

生：如圖2，在△ABC中，∠C=90°，設∠A=30°，BC=a，則AB=2a，AC= 3 a，所以

sin 30°= BC AB = a 2a = 1 2 ，

sin 60°= AC AB =? 3? 2 ，

cos 30°= AC AB =? 3? 2 ，

cos 60°= BC AB = 1 2 .

生：同理，如圖3，在△ABC中，∠C=90°，設∠A=45°，BC=a，則AC=a，AB= 2 a，可得

sin 45°= BC AB =? 2? 2 ，

cos 45°= AC AB =? 2? 2 .

小組3：我們學習了∠A的正弦、余弦、正切和余切，那么這幾個三角函數之間又有什么關系呢？

師：這個問題提得很好，特別注重了知識之間的聯系，那么，你們有什么發現嗎？

生：我們知道sin A= a c ，cos A= b c ，

tan A= a b ，cot A= b a .

如果sin A÷cos A= a c ÷ b c = a b? ，而tan A= a b ，即sin A÷cos A=tan A.

同理cos A÷sin A=cot A.

師：真不錯！我相信只要同學們肯動腦筋，善于觀察、勤于研究，就一定能夠發現數學知識的聯系無處不在.我也相信努力學習、善于發現的你們潛力無限，一定能闖出屬于自己的一片新天地.

（六）反思小結，歸納提升

師：本節課，我們在學習了正弦和余弦的相關知識的同時，還學到了提出問題的方法，相信每一名學生都會有所收獲.那么，哪名學生能具體說一說你本節課有哪些收貨？

生A：我們通過學習，發現可以用三種數學語言（符號語言、文字語言、圖形語言）來表示正弦和余弦的定義和性質，并且它們之間可以轉換.我覺得數學非常有趣，現在更愿意學習數學了.

生B：學習時要注意尋找數學知識之間的聯系，可以運用類比的方法自己設計問題，一題多變，觸類旁通.

生C：要多觀察、多思考、多交流，從不和諧處找問題、發現問題、提出問題，并分析問題、解決問題.

生D：在學習時，只有善于發現問題、提出問題，才能更好地解決問題，這樣不僅有助于提高我們學習數學的能力，更有助于提升我們的數學素養.

……

三、教學反思

1.新時代對廣大教師提出了更高的要求，要求教師不僅要教會學生做“答”，更要教會學生提“問”.因此，在具體的教學中，教師要給學生留有足夠的空間，為學生創設一個良好的學習環境，鼓勵學生創造性提出問題，并逐步學會發現問題和提出問題的方法，進而培養學生分析問題、解決問題的能力.教師要相信只要給學生一個支點，他們就能撬起整個地球！

2.啟發式教學注定會替代“灌輸式”“填鴨式”教學，教師不能過多地替代學生，而應適時引導、啟發學生發現問題、提出問題，給學生更多的發言機會，相信“創造性”火花會在課堂上形成激烈的碰撞，激發出學生的積極思維，迸發出學生無限潛能.同時，作為教師的我們也能得以提升，從而推動師生共同進步，共同成長，教學相長將不再成為空談.

3.有學生在課后小記中寫道：“這節課教師讓我們自己提出問題、設計問題，我真正體會到了學習的快樂，體會到了發現的樂趣和成功的喜悅，學起來挺輕松、特來勁，原來枯燥的數學還可以這樣學，我對學好數學更有信心了.”實踐證明，在教學中，教師只要敢于改變，創造機會讓學生主動學習、自主學習，讓學生帶著問題去學習，使其真正成為學習的主人，就一定能激發學生學習數學的興趣，引導學生創造性學習，培養學生的創新意識，激發學生的創新思維，提升學生的創新能力.只有這樣，“以學生發展為本”的教學理念才不會成為“空中樓閣” ，肯定會在教學中生根發芽，開出絢麗多姿的花朵.