高中數學解題中數形結合思想的應用分析

曹艷

【摘要】數學問題的解答中，數和形是密不可分的，同時它們也是抽象與直觀的具體展現.高中數學的學習中，數與形是兩個最基礎的概念，高中數學知識也是緊緊圍繞這兩個概念進行拓展的.運用數形結合思想不但可以有效提升學生的理解能力，同時可以培養學生的數學核心素養.鑒于此，本文首先闡述了高中數學解題中數形結合思想應用的不足之處，并論述了該種思想在解題中的具體應用，以供參考.

【關鍵詞】高中;數學;數形結合

引 言

當前，高中教師在講解相關數學問題時，大多數只是對題目中的相關知識進行講解，而忽略了相應解題方法的傳授過程.事實上，學生在數學習題的解答中能夠體會到相應習題的解題方法，這也是高中數學解題教學的重要目標.而數形結合是利用圖像實現數與圖形之間的轉換，它能夠使問題變得更加直觀.所以，高中數學習題解答中，教師要大力講解此種方法的應用，幫助學生更好地解答相關數學問題.高中是學生學習與成長過程中至關重要的轉折階段，在這一時期，學生的學業壓力較重，學習難度較大，在數學解題中會遇到很多難題，這些難題教師必須幫助其解決，從而降低學生的學習困難，幫助學生放松身心，提升學生的學習效率和解題準確度.

一、數形結合思想在高中數學解題應用中存在的問題

（一）數學教學思維比較淺顯

高中數學中，數形結合是一種很好的解題方法，然而學生對其的理解不夠深入，與此同時，高中數學教學中也存在教學思維較為膚淺的情況，這造成學生在解決一些較為抽象的數學問題時感到束手無策.正因如此，學生解答一些數學問題的過程中，通常只是結合題目中給出的條件，無法實現對它們的良好轉化，導致學生探索問題能力的不足，數學能力得不到良好的提升.此外，一些學生不具備良好的抽象思維，只會解答部分淺顯易懂的問題，在面對那些較為復雜的問題時，通常不得其法，無法抓住問題的關鍵所在.

（二）學生數學思維的差異性

每個學生的數學基礎不同，這樣他們在解答數學習題的過程中思維也會有所不同，并且每個學生的思維方式也存在一定差異，這導致解答相應數學問題的過程中，其認識的程度和理解的深度會存在一定差異.另外，一些學生在解答數學習題的過程中沒有充分發掘題目中的隱藏條件，給解答帶來一定阻礙.

二、數形結合思想在高中數學解題中的應用價值

（一）有利于幫助學生理解數學概念

高中數學知識涵蓋很多數學概念和數學定義，高中數學與初中和小學數學相比，具有較大的學習難度，抽象化的數學概念逐漸增加，有一些可能會超出學生的理解能力和接受范圍.因此，在高中數學教學和解題中應用數形結合思想，有利于幫助學生理解抽象化的數學概念，將抽象化的數學概念以另一種學生能夠輕松理解的形式進行呈現，這不僅可以有效提升學生的學習水平，還能在降低學生理解數學概念難度的同時培養學生的學習自信，端正學生的學習心態.通過數形結合還能夠培養學生的數學思維和數學意識，引導學生用數學思想思考問題，培養學生的數學思維，推動學生學習能力的提升，提高學生的聯想力，不斷促進學生綜合素養的提升.

（二）有利于幫助學生學習更多的解題方法

對于高中生來說，他們面臨的學業壓力比較重，同時要為高考做準備，因此時時刻刻都不能放松，為此教師一定要幫助學生減輕學業壓力，提高學習效率，而引導學生運用更加有效地方式來解決數學問題就是一個有效的途徑.數形結合思想是一種經常會使用的解題方式，學生如果能夠扎實地掌握這一思想和方法，并且能夠將其靈活地應用于數學解題過程中，那么學生的學習效率會有很大幅度的提升.教師通過教學數形結合思想的應用能夠幫助學生掌握更加有效的解題方法，不斷推動學生學習水平與解題能力的進步，提高學生的數學綜合素養.

三、數形結合思想在高中數學解題中的具體應用

（一）數形結合思想在方程式中的應用

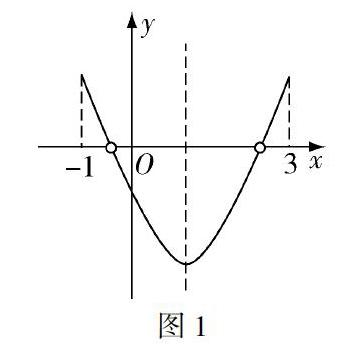
在對一元二次方程根的情況進行研究的過程中，我們通常會結合二次函數的圖像.如二次函數的解析式為y=ax2+bx+c（a≠0），我們在對方程ax2+bx+c=0求根時，也就是令y=0，實際上就是函數的縱坐標為0，求其與x軸的交點，這樣問題便得到一定轉化，能夠得到很好的解決.例如下面這道例題，“已知方程x2+4mx+6m=0，它的兩個根在區間（-1，3）中，求m的取值范圍.”在解答這道習題的過程中，我們就可以應用數形結合思想.假定f（x）=x2+4mx+6m，這樣便實現了方程到函數的轉化過程.我們可以根據題目中的要求畫出該二次函數的簡圖，如圖1所示.

方程x2+4mx+6m=0的兩個根在區間（-1，3）中，實際上就是f（x）=0時，二次函數與x軸焦點的橫坐標在區間（-1，3）之間.借助于這個圖像，我們能夠得知，要想使題目中的條件得以成立，必須同時滿足f（-1）>0，f（3）>0，f? -b[]2a =f（-2m）<0.將這幾個不等式聯立，最終得到答案- 1[]2 3[]2 .

（二）數形結合思想在集合問題中的應用

高中數學中包含眾多知識點，集合、函數、不等式、數列……其中集合是其他函數的基礎，只有學好集合，才能夠更加良好地進行后續知識的學習.集合習題的解答中，因為一些問題單純靠頭腦的想象存在一定困難，而利用圖形能夠使問題變得更加直觀，所以數形結合思想也是集合問題解答中經常會用到的一種方法.

例如，“已知集合A={x|x<-1或x≥1}，B={x|2a<x<a+1}，a<1，且B∈A，求a的取值范圍.”首先2a<x<a+1，要想使其成立，就需要保證2a<a+1，由此得出a<1，而題目中也給出了a<1的已知條件，說明集合B不是空集.我們又可以結合題意畫出相應數軸，如圖2所示.

（三）數形結合思想在解析幾何中的應用

利用坐標系可加強數和形之間的關聯性，實現從數到形的轉換，從而使問題得到有效解決.例如，“已知x，y滿足方程 x2 16 + y2 25 =1，求y-3x的最小值和最大值是多少.”在這道習題的解答中，如果運用普通的代數求解方法，問題難以得到解決，而通過數形結合的方法能夠化繁為簡，問題得到良好解決.首先假定y-3x=a，可以得出y=3x+a，這樣原問題便得到轉化，變為在橢圓 x2 16 + y2 25 =1上求取一點，通過這一點直線的斜率是3，求其在y軸上截距的最小值和最大值，這樣我們便可以畫出如圖3所示圖形.

從圖像中我們可以看出，在直線與橢圓相切時，截距最大或最小.于是我們可以聯立兩個方程式，得出169x2+96ax+16a2-400=0，再令根的判別式Δ=0，這樣可以得出a=±13，所以y-3x的最小值為-13，最大值為13.

（四）數形結合在函數問題中的應用

函數是高中數學中一個重要的知識點，也是高考必考的知識點，函數中包含很多數學概念，函數的種類也有很多，比如三角函數、指數函數等，而縱觀高中數學的應用題題型，函數應用題是經常出現的一個典型題型.針對函數問題的解題通常是要先建立一個直角坐標系，通過直角坐標系分析已知條件之間的關系，然后在直角坐標系中通過各種條件來繪制函數圖像，因此函數問題中經常能用到數形結合思想，這不僅是解題的關鍵步驟，通過圖像將比較抽象的函數關系呈現出來，能夠幫助學生提高解題效率.例如，“已知方程|x2-4x+3|-a=0有三個不相等的實數根，求a的值.”針對這道函數題，教師應該引導學生利用數形結合思想來解題，通過圖像分析方程根的不同情況.教師要先要求學生繪制出y=|x2-4x+3|的圖像，通過圖像來觀察交點，其交點就是方程的解，也是函數的值，這樣會大大降低學生的解題難度，同時可以增強學生的自信心.

（五）數形結合在提高算理能力中的應用

在高中數學解題中，學生一定要對每一種算法的由來及原理的推理過程有一個初步的認識和掌握，這樣才能改變死記硬背的記憶方式，加深學生對于數學算法及數學原理的理解和記憶.學生如果真正掌握了一個數學算法的原理及推理過程，在應用的過程中也能夠更加得心應手，從而有效減少計算中因計算原理出現的錯誤.教師不能只關注學生最后的計算結果，而應該深入了解學生的計算過程，幫助學生在計算的過程中掌握良好的計算技巧，縮短學生的計算時間，提高計算的準確率.為了達到這一教學目標，教師就可以充分借助數形結合思想的優勢.

四、應用數形結合思想解題的注意事項

對于數形結合在高中數學解題中的應用，教師要將教材作為基本點進行研究，深入挖掘教材，從而適當融入數形結合思想.對于數形結合思想在高中數學解題中的應用，教師要將所有的應用形式都立足于教材之上，且要對教材內容進行深入的研究和分析，尋找教材中能夠應用數形結合思想的契機.并不是每一個數學知識都能夠應用到數形結合思想進行教學，如果教師強硬地將數形結合思想融入不適當的地方，很容易造成相反的效果，影響高中數學教學的質量.因此，教師要對教材內容進行全面研究，多思考，多實踐，將理論與實踐相結合，在教學中總結經驗，吸取教訓，引導學生正確使用數形結合思想.

另一方面，教師針對數形結合思想的應用要選擇合適的方式進行滲透，也就是說，要針對學生的接受能力、數學基礎等多方面進行綜合性考慮，當學生對于數形結合思想產生一些不理解的問題時，教師要將教學節奏放慢，采取靈活的教學形式讓學生理解數形結合思想的應用方式，從而真正發揮數形結合思想的教育價值，提高學生的解題能力.

綜上所述，我們可以看出，在高中數學解題教學中應用數形結合思想，能夠顯著提升教師的教學質量與效果.然而，在實際應用這種思想的過程中，因為一些人為以及理解上的不足等原因，導致該種思想的真正價值并沒有得以真正體現.因此，作為一名教師，要肩負起重任，對學生加以引導與激勵，發現學生解題中的錯誤要及時予以糾正，保證學生在解答相關數學問題時能夠良好地應用數形結合思想，從而達到提升他們數學能力的重要目標.

【參考文獻】

[1]楊克利.探析高中數學解題中數形結合思想的應用[J].中國校外教育，2019（27）：118.

[2]李天歌.高中數學解題中數形結合思想的運用探索[J].科技創新導報，2017（20）：227-228.

[3]李貞凌.數形結合思想方法在高中數學教學與解題中的應用[J].學周刊，2017（27）：110，81.

[4]孔令偉.數形結合思想方法在高中數學教學與解題中的應用[D].遼寧師范大學，2012.