基于不同價值取向的復(fù)習(xí)課教學(xué)設(shè)計案例分析

黃永明 何恩榮 葉丹

[摘? 要] 數(shù)學(xué)教學(xué)設(shè)計是對數(shù)學(xué)教學(xué)活動的構(gòu)想，是數(shù)學(xué)教學(xué)活動順利進行的基本保證. 文章分析三個不同價值取向的數(shù)學(xué)復(fù)習(xí)課教學(xué)設(shè)計，指出每種價值取向教學(xué)設(shè)計的特點，并結(jié)合案例對數(shù)學(xué)復(fù)習(xí)課教學(xué)設(shè)計提出建議.

[關(guān)鍵詞] 初中數(shù)學(xué);復(fù)習(xí)課;教學(xué)設(shè)計;價值取向;全等三角形

■ 前言

教學(xué)設(shè)計的價值取向是教師綜合考慮學(xué)生狀況、教學(xué)內(nèi)容特點、教學(xué)條件等因素而選擇的教學(xué)目標(biāo)定位，是教師教育價值觀在教學(xué)中的體現(xiàn)，而在初中數(shù)學(xué)教學(xué)中，教師對復(fù)習(xí)課的教學(xué)設(shè)計不夠重視. 本文分析昆明市某中學(xué)開展“同課異構(gòu)”時三位教師不同價值取向的數(shù)學(xué)復(fù)習(xí)課教學(xué)設(shè)計，復(fù)習(xí)內(nèi)容是人教版八年級上冊“全等三角形的判定”.

三個教學(xué)設(shè)計的價值取向分別為知識技能為主、過程方法為主、知識技能和過程方法相結(jié)合. 本文呈現(xiàn)三個教學(xué)設(shè)計的教學(xué)流程，并在對流程進行細(xì)化的過程中分析其價值取向，再結(jié)合教學(xué)設(shè)計的部分片段具體分析其價值體現(xiàn)，最后對數(shù)學(xué)復(fù)習(xí)課的教學(xué)設(shè)計提出建議.

■ 教學(xué)設(shè)計案例的價值取向分析

教學(xué)設(shè)計的價值取向主要體現(xiàn)在教學(xué)目標(biāo)的設(shè)計上. 《數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》提出課程目標(biāo)的四個方面：知識技能、數(shù)學(xué)思考、問題解決、情感態(tài)度，雖然沒提到“過程方法”[1]，但卻通過“數(shù)學(xué)思考”和“問題解決”將其具體化[2]■，所以在探討“過程方法”時，我們從“數(shù)學(xué)思考”和“問題解決”兩個方面進行分析. 三個教學(xué)設(shè)計的目標(biāo)定位不同，側(cè)重課程目標(biāo)的不同維度，體現(xiàn)出不同的價值取向，但也沒有忽視其他維度的目標(biāo)，課程目標(biāo)的四個方面是不可分割的.

1. 案例1：知識技能為主要價值取向的教學(xué)設(shè)計

（1）教學(xué)流程分析

教學(xué)目標(biāo)為：復(fù)習(xí)重點內(nèi)容，形成知識體系，會利用全等三角形相關(guān)知識解決問題;在題組訓(xùn)練過程中挖掘隱藏條件并總結(jié)證明方法. 教學(xué)流程如表1.

該設(shè)計通過習(xí)題訓(xùn)練鞏固基礎(chǔ)知識，促進學(xué)生基本技能的掌握. 價值取向主要體現(xiàn)在：第一，自主學(xué)習(xí)環(huán)節(jié)，填寫導(dǎo)學(xué)案，讓學(xué)生回憶知識，為運用知識解決問題奠定基礎(chǔ);第二，師生互動過程中，六個例題承載著聯(lián)系基礎(chǔ)知識與基本技能的功能，使學(xué)生在解題的過程中再次鞏固基礎(chǔ)知識，形成基本的證明思路;第三，當(dāng)堂練習(xí)，補充隱藏條件，提高學(xué)生運用知識的能力，強化技能. 整個教學(xué)過程的設(shè)計符合課標(biāo)對知識技能維度目標(biāo)提出的要求.

“教，上所施，下所效也”，教師將教學(xué)目標(biāo)定位為以知識技能為主，設(shè)計以習(xí)題為主線，在訓(xùn)練過程中教師講解、示范、提問，學(xué)生接受、模仿、練習(xí)，知識點覆蓋較全，有利于教師對整節(jié)課的時間安排. 該價值取向的教學(xué)設(shè)計適用于基礎(chǔ)薄弱的學(xué)生，以陳述性知識為主的復(fù)習(xí)內(nèi)容，使學(xué)生牢固掌握基礎(chǔ)知識與基本技能.

（2）設(shè)計片段展示（師生互動部分）

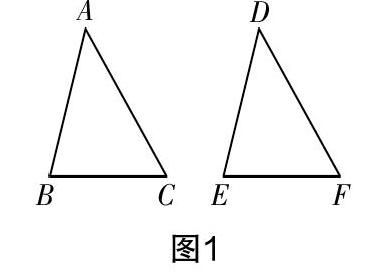
例1？搖 如圖1，下列條件可以判定△ABC≌△DEF的是（? ? ？）

A. ∠A=∠D? ?∠B=∠E? ? ?∠C=∠F

B.? AB=DE? ?∠B=∠E? ? ?AC=DF

C.∠A=∠D? ? ∠B=∠E? ? AC=DF

例2? 在△ABC和△DEF中，已知∠C=∠D，∠B=∠E，要判定這兩個三角形全等，還需要條件（？? ? ）

A. AB=ED? ?B. AB=FD

C. AC=FD? ?D.∠A=∠F

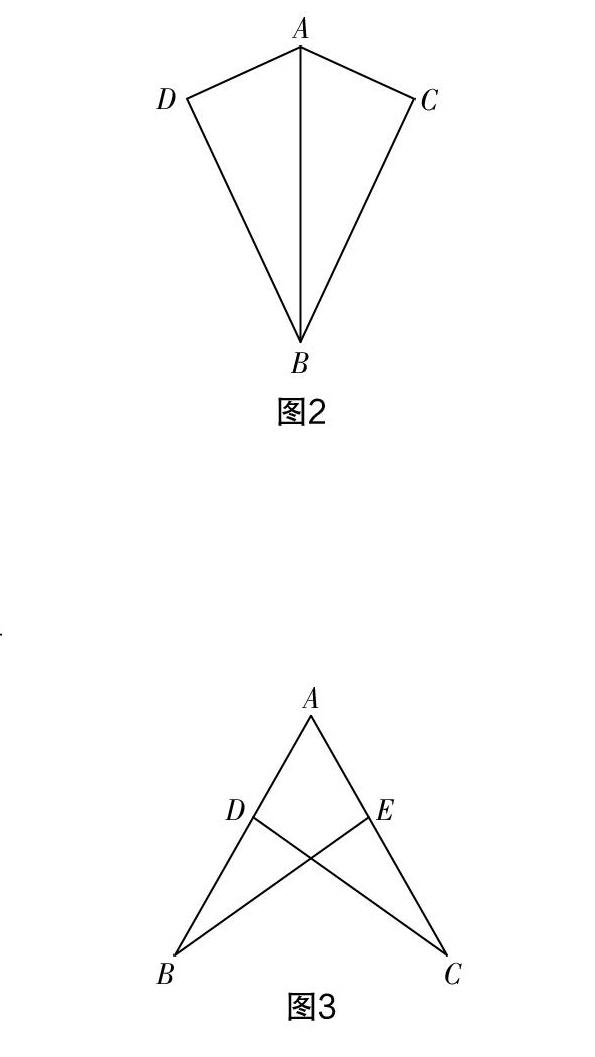
例3 如圖2，已知AD=AC，要使△ADB≌△ACB，需要添加的條件是__________.隱藏條件：____________.

例4 如圖3，已知∠B=∠C，要使△ADC≌△AEB，需要添加的條件是______. 隱藏條件：_____________.

……

該片段呈現(xiàn)了“師生互動”環(huán)節(jié)中的四個例題. 可以看出，例1、例2鞏固基礎(chǔ)知識，澄清知識混淆;例3、例4擴展解題思路，訓(xùn)練學(xué)生的解題技能，學(xué)生能運用規(guī)則進行操作. 在例題的訓(xùn)練中使學(xué)生發(fā)現(xiàn)隱藏條件，培養(yǎng)學(xué)生運用知識解決問題的能力，較好地處理了知識傳授與能力培養(yǎng)的關(guān)系.

2. 案例2：過程方法為主要價值取向的教學(xué)設(shè)計

（1）教學(xué)流程分析

教學(xué)目標(biāo)為：學(xué)生能熟練證明兩個三角形全等，通過開放題的探究使學(xué)生掌握隱藏條件，能在具體問題中合理選擇相應(yīng)的判定方法. 教學(xué)流程如表2.

該設(shè)計旨在讓學(xué)生在尋找隱藏條件的過程中形成證明思路，找到證明方法. 價值取向主要體現(xiàn)在：第一，復(fù)習(xí)引入，學(xué)生經(jīng)歷口頭復(fù)習(xí)、歸納形成思維導(dǎo)圖的過程，鍛煉學(xué)生清晰地進行語言表達的能力;第二，教師利用三個開放題，引導(dǎo)學(xué)生發(fā)現(xiàn)隱藏條件，發(fā)展學(xué)生合情推理和演繹推理的能力，使學(xué)生掌握分析和解決問題的基本方法，該教學(xué)設(shè)計注重過程方法，除了讓學(xué)生探究隱藏條件之外，還帶領(lǐng)學(xué)生挖掘隱藏條件的來源（平移、翻折、旋轉(zhuǎn)），進一步讓學(xué)生體會知識的發(fā)生發(fā)展過程;第三，在三個綜合題的訓(xùn)練過程中，學(xué)生借助隱藏條件解決問題，將方法內(nèi)化到學(xué)生的知識、能力體系里，再遇到類似的問題時可以輕松應(yīng)對. 該教學(xué)設(shè)計注重讓學(xué)生在獲取知識的過程中發(fā)展各方面的能力，整個教學(xué)過程的設(shè)計符合課標(biāo)對過程方法維度目標(biāo)提出的要求.

“引而伸之，觸類而長之”，教師將教學(xué)目標(biāo)定位為以過程方法為主，引導(dǎo)學(xué)生在學(xué)習(xí)的過程中獲得解決問題的一般方法. 該價值取向的教學(xué)設(shè)計適用于基礎(chǔ)一般的學(xué)生，可以通過一些元認(rèn)知反思活動來提高學(xué)生的數(shù)學(xué)能力.

（2）設(shè)計片段展示（運用開放式條件，梳理證明三角形全等的思路）

如圖4，已知AD=AC，要使△ADB≌△ACB，要添加的條件是__________.

如圖5，已知AB=AC，要使△ABE≌△ACD，要添加的條件是__________.

如圖6，已知∠A=∠D，要使△ABO≌△DCO，要添加的條件是_______.

師：同學(xué)們獨立完成以上三個題. （巡視解題情況，針對圖4展示幾個同學(xué)的結(jié)果）

甲：添加條件DB=CB（SSS）或∠DAB=∠CAB（SAS）.

乙：添加條件∠DAB=∠CAB.

丙：添加條件DB=CB.

師：丙說說是怎么做的.

丙：已知一組邊長相等，又有一條公共邊，就想到了SSS這種證明方法，我就添加了DB=DC.

師：乙又是怎么做的呢？

乙：已知一組邊長相等，還有一條公共邊，所以我想再加一個夾角就可以湊出SAS.

師：兩個同學(xué)回答得都很好，但是考慮問題不全面，甲正好是綜合了兩個同學(xué)的答案，考慮比較全面，我們請甲來說說他的解題思路.

甲：題目條件顯示有一組邊長相等，又有一條公共邊，相當(dāng)于共有兩個已知條件（SS），在證明全等三角形的5種方法里，對于一般三角形而言，包含了SS的有SAS、SSS，所以我就想到要加這兩個條件.

師：甲考慮得很全面，我們在思考題目的時候要面面俱到. 那么接下來再給同學(xué)們一點時間，完善這幾個題目，要全面考慮哦.

……

該片段展示了“用開放題，梳理證明思路”環(huán)節(jié)中設(shè)計的三個開放題及教師對該環(huán)節(jié)的預(yù)設(shè)情形. 教師充分預(yù)設(shè)學(xué)生可能出現(xiàn)的答案，利用課堂上的生成性資源，讓學(xué)生再現(xiàn)解題過程，提高學(xué)生的反思能力，促進知識的遷移、深化和鞏固，學(xué)生相互完善答案，在審視自己思維發(fā)生過程的同時對他人提出的問題進行反思，形成全面思考問題的意識，最后總結(jié)解決問題的方法. 該設(shè)計在運用知識解決問題的過程中注重發(fā)展學(xué)生的思維能力和元認(rèn)知能力，讓學(xué)生經(jīng)歷方法的形成、發(fā)展過程，獲得解決問題的一般方法.

3. 案例3：知識技能和過程方法相結(jié)合為主要價值取向的教學(xué)設(shè)計

（1）教學(xué)流程分析

教學(xué)目標(biāo)為：知道全等三角形的概念與性質(zhì)，能靈活運用全等三角形的判定定理;體驗數(shù)學(xué)活動的探索性和創(chuàng)造性，感受證明的必要性、證明過程的嚴(yán)謹(jǐn)性. 教學(xué)流程如表3.

該設(shè)計通過創(chuàng)造性活動，使學(xué)生獲得活動經(jīng)驗，從中感悟數(shù)學(xué)思想. 其價值取向主要體現(xiàn)在：第一，復(fù)習(xí)回顧，學(xué)生動手繪制思維導(dǎo)圖，自主構(gòu)建知識網(wǎng)絡(luò)，既能復(fù)習(xí)相關(guān)知識，又能提高歸納總結(jié)能力;第二，在拼圖活動中，學(xué)生從圖形與幾何的角度發(fā)現(xiàn)和提出問題，經(jīng)歷借助圖形思考問題的過程，初步建立幾何直觀[1]，并在活動中發(fā)現(xiàn)全等三角形的本質(zhì)屬性，強化學(xué)生對全等三角形定義和性質(zhì)的認(rèn)識;第三，問題探究過程中，利用一個開放題，培養(yǎng)學(xué)生的探索和團隊合作能力，讓其經(jīng)歷從不同角度尋求解決問題的方法的過程[1]，并從中提煉出證明方法;第四，在變式訓(xùn)練環(huán)節(jié)，鞏固基礎(chǔ)知識，增強學(xué)生的應(yīng)用意識，提高學(xué)生的基本能力.

數(shù)學(xué)教學(xué)踐行“以人為本”的教育理念，從學(xué)生的需要出發(fā)，教師將教學(xué)目標(biāo)定位為以知識技能和過程方法為主，尊重知識的發(fā)生、發(fā)展過程，獲得解決數(shù)學(xué)問題的方法. 該價值取向的教學(xué)設(shè)計適用于基礎(chǔ)較好的學(xué)生，以程序性知識為主的復(fù)習(xí)內(nèi)容，實現(xiàn)學(xué)生對數(shù)學(xué)問題的感性認(rèn)識到理性認(rèn)識的升華.

（2）設(shè)計片段展示（問題探究部分）

例題：如圖7，選擇條件，證明兩個三角形全等：①AB=DC;②AC=DB;③AO=DO;④∠A=∠D;⑤∠ABC=∠DCB. 選擇條件_______，可以證明________.

師：同學(xué)們觀察一下圖形，覺得哪兩個三角形會全等？

生1：老師，這個題目不止一組全等三角形.

師：有哪幾組？

生1：△ABC和△DCB.

師：還有嗎？

生2：△AOB和△COD.

師：請注意對應(yīng)關(guān)系.

生3：△ABC和△DCB.

師：還有嗎？

生眾：沒有了.

師：從這個圖中我們能得到哪些條件？

生4：BC是公共邊，∠AOB和∠DOC是對頂角.

師：給大家10分鐘時間，小組合作討論，有哪些證明方法？

生5：證明△ABC和△DCB有5種，分別是……

生6：證明△AOB和△DOC有3種，分別是……

……

該片段展示了“問題探究”環(huán)節(jié)的例題，教師用開放題引導(dǎo)學(xué)生多角度進行分析，培養(yǎng)學(xué)生的發(fā)散思維，提高學(xué)生的創(chuàng)造力. 學(xué)生經(jīng)歷探究活動的過程，積累活動經(jīng)驗，將知識轉(zhuǎn)化為能力. 教師先強調(diào)對應(yīng)關(guān)系，提示隱藏條件，然后放手讓學(xué)生探索，既關(guān)注學(xué)生的知識與技能，也注重過程方法，注重學(xué)生分析問題和解決問題能力的培養(yǎng)，提高學(xué)生靈活運用知識的能力.

■ 結(jié)論與建議

1. 結(jié)論

教師選擇什么樣的價值取向來指導(dǎo)復(fù)習(xí)課教學(xué)設(shè)計，將影響教師的課堂教學(xué)行動與學(xué)生的學(xué)習(xí)結(jié)果[3]. 通過對不同價值取向的三個復(fù)習(xí)課教學(xué)設(shè)計的分析，可以看出每種價值取向的復(fù)習(xí)課教學(xué)設(shè)計都有其存在的意義.

以“知識技能”為主要價值取向的復(fù)習(xí)課教學(xué)設(shè)計，是在幫助學(xué)生全面梳理相關(guān)知識的基礎(chǔ)上設(shè)置例題，使學(xué)生能運用規(guī)則進行操作，習(xí)得并強化技能，從而達成復(fù)習(xí)目標(biāo);以“過程方法”為主要價值取向的復(fù)習(xí)課教學(xué)設(shè)計，注重學(xué)生元認(rèn)知能力的培養(yǎng)，對解題過程進行反思，發(fā)現(xiàn)解題規(guī)律，總結(jié)解題方法，從而達成復(fù)習(xí)目標(biāo);以“知識技能和過程方法”為主要價值取向的復(fù)習(xí)課教學(xué)設(shè)計，在復(fù)習(xí)內(nèi)容的基礎(chǔ)上通過探究性活動促進學(xué)生思考，培養(yǎng)學(xué)生動手與動腦能力，使學(xué)生從對數(shù)學(xué)的感性認(rèn)識上升到理性認(rèn)識，在“怎么做”與“為什么這樣做”之間搭起橋梁，從而達成復(fù)習(xí)目標(biāo).

2. 建議

如何評價數(shù)學(xué)教學(xué)設(shè)計的優(yōu)與劣，沒有絕對統(tǒng)一的標(biāo)準(zhǔn)，因為任何一個教學(xué)設(shè)計均有特定的教學(xué)功能，反映著某種教育價值取向. 三個教學(xué)設(shè)計都有各自的特點，教師在進行數(shù)學(xué)復(fù)習(xí)課的教學(xué)設(shè)計時，應(yīng)根據(jù)學(xué)生情況、復(fù)習(xí)內(nèi)容、教學(xué)條件等來選擇價值取向，確定教學(xué)目標(biāo). 教師要弄清楚“為什么學(xué)”和“如何學(xué)”這兩個問題，解決好“教什么”“怎么教”“達到什么效果”的問題. 這些是數(shù)學(xué)教學(xué)設(shè)計的核心問題[4]. 根據(jù)對以上三個教學(xué)設(shè)計的分析，筆者對數(shù)學(xué)復(fù)習(xí)課的教學(xué)設(shè)計提出以下建議：

第一，注重知識網(wǎng)絡(luò)的構(gòu)建. 復(fù)習(xí)是一個“溫故而知新”的過程，學(xué)生在復(fù)習(xí)課上總結(jié)知識，提煉數(shù)學(xué)思想方法，從而獲得新的理解與體會. 教師不能通過提問題的方式剝奪學(xué)生自主建構(gòu)知識網(wǎng)絡(luò)的過程，而要讓學(xué)生自主構(gòu)建知識網(wǎng)絡(luò)，理清知識間的聯(lián)系，從而更好地理解和記憶知識.

第二，關(guān)注復(fù)習(xí)的內(nèi)容. 復(fù)習(xí)內(nèi)容應(yīng)該合理安排，要做到有的放矢. 復(fù)習(xí)課需要練習(xí)，但與習(xí)題課不同，對于例題、習(xí)題的選擇應(yīng)該緊緊圍繞復(fù)習(xí)的主要內(nèi)容，做到不重不漏、題型多樣、合理有序、題量適中.

第三，合理預(yù)設(shè)，把握課堂進度. 教學(xué)設(shè)計是課堂活動的“預(yù)設(shè)”，然而“預(yù)設(shè)”與“生成”總是存在差異，教師要充分預(yù)設(shè)，巧妙應(yīng)對. 課堂需要適當(dāng)留白，便于教師更好地把握課堂進度.

第四，滲透數(shù)學(xué)思想. 復(fù)習(xí)課可以幫助學(xué)生揭示解題規(guī)律，總結(jié)解題方法，這就要求教師在講解的過程中，適當(dāng)滲透一些數(shù)學(xué)思想方法，使學(xué)生學(xué)會舉一反三，進一步提高學(xué)生運用所學(xué)知識分析和解決問題的能力.

參考文獻：

[1]中華人民共和國教育部. 義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）[M]. 北京：北京師范大學(xué)出版社，2012.

[2]姚國平. 課堂教學(xué)目標(biāo)設(shè)計的追求——三維目標(biāo)價值取向[J].教育實踐與研究（B），2011（08）.

[3]楊梓生. 以認(rèn)知與思維轉(zhuǎn)化為價值取向的教學(xué)設(shè)計[J]. 福建教育，2015（37）.

[4]何小亞，姚靜. 中學(xué)數(shù)學(xué)教學(xué)設(shè)計[M]. 北京：科學(xué)出版社，2017.